无人机FSO/RF 混合中继链路传输速率优化方法

邵龙，李勇军，李信，王猛，宋鑫康，唐翰玲，赵尚弘

（1.空军工程大学 信息与导航学院，陕西 西安 710077；2.中国人民解放军93658部队，北京 100000）

引言

随着移动用户数量的高速增长及用户对于通信速率需求日趋，传统通信手段已经无法满足用户对于高带宽、低时延的需求[1]。在灾后恢复、偏远地区的通信保障以及无人机巡逻等军事行动时[2]，无人机可以利用其良好的机动性突破地形限制，从而覆盖通信暂时陷入瘫痪的区域，帮助用户迅速恢复正常通信。现今射频(ratio frequency,RF)通信频谱已相当密集，很难通过增加更多带宽来满足当前用户急速增长的通信需求。自由空间光（free space optical,FSO）通信作为射频通信系统的一个很好的替代方案，具有带宽大、数据速率高和通信链路可靠[3]、保密性较高[4]等优点。激光通信载荷材料较轻，符合无人机平台轻量化的要求[5]。基于无人机的FSO/RF 混合通信技术应运而生，FSO 链路发挥现有地面通信系统中光纤通信的角色，拥有大带宽和极高传输速率[6]。近年来，由于两种技术结合所带来的成本可控以及保密性强的优点，RF/FSO 混合通信成为了一种具有广阔前景的通信模式[7,8]。

对于无人机中继链路通信速率的研究，按照无人机是否移动分为固定式中继和移动中继，按照链路不同分为RF/RF 和FSO/RF 混合链路。无人机中继链路主要分为3 种：1）无人机中继两端链路均为光通信链路，在信道适应光传输，即能见度等参数较好的情况下链路传输速率非常高，且不受电磁频谱的限制，但是在光链路信道质量不佳时传输速率会急剧恶化甚至达到不能使用的地步；2）无人机中继两端都为射频通信链路，此种链路的优势是全向天线的制作较为成熟，通信的距离较远，且受天气状况的影响较光通信链路来说较小，但也存在通链路速率不够高且容易受电磁干扰和频谱的限制；3）无人机中继两端中一端为光通信链路，一端为射频通信链路，结合光通信传输速率大及射频通信灵活接入的优势，能够在特定情况例如光通信链路质量欠佳的情况下仍维持一定的通信速率。对于无人机作为中继节点的链路，研究首先集中在两端都为RF 链路的情况，通过算法优化提升总体链路的性能。在无人机中继的RF/RF 链路模型中，2014 年ALHOURANI A 等人[9]通过改变空中平台高度的方式来提升其覆盖范围，保障偏远地区或灾后地区基本通信；2016 年BORYALINIZ R I 等人发表会议论文[10]，建立了低空无人机协助蜂窝网络模型，得出了高效的空中基站位置优化算法；ZENG Y 等人[11]在2016 年研究了目的节点固定时通过无人机的轨迹及功率的优化来最大化信道的通信速率；2017 年引入了一种实用的圆形无人机轨迹[12]，优化无人机的飞行半径、初始/最终位置和速度以及最大速度和加速度，使通信能量效率最大化，显著提高无人机通信的能源效率；2021 年LUO W 等人[13]建立了双跳多无人机中继RF/RF 通信系统，创新性地提出了LoS（line of sight）概率通道模型，其通过对无人机轨迹的优化，达到最小数据采集率的目标。在无人机中继的FSO/RF 混合链路模型中，2021 年吴琰等人[14]通过设置不同的副载波调制方式、湍流强度、指向性误差及RF 信道衰弱参数，分别分析混合FSO/RF系统和单FSO 系统的误码率和中断概率，得出FSO/RF 对于单FSO 链路的效率优势；2022 年XU G 等人[15]对FSO/RF 链路中的中断概率以及平均误码率，提出了端到端系统的累积分布函数和概率密度函数等新的解析表达式，其中FSO 链路采用Málaga 衰落模型，RF 链路采用κ-μ衰落模型；2020 年PHAM Q V 等人[16]建立了无人机辅助的可见光通信，利用非正交多址(non-orthogonal multiple access,NOMA)技术、机器学习技术对功率、位置等优化参数进行求解，提高了算法效率；2021 年LEE J H 等人[17]针对不同用户对时延要求及FSO和RF 信道速率不匹配问题，通过在无人机平台上加装缓冲区和无人机位置的优化，提升混合链路总体传输速率；2022 年TRAN D H 等人[18]建立了基于后向散射和缓存技术的无线驱动无人机通信网络，使用动态时间分割(dynamic time splitting,DTS)方法向无人机驱动的供电或发送信息，通过联合优化DTS 比率和UB 的轨迹，最大化总吞吐量。

综上，已有文献对于FSO/RF 链路无人机位置坐标及功率分配联合优化以提高总体链路传输速率的研究较少。针对这个问题本文建立了双跳FSO/RF 通信链路模型，以无人机作为中继，服务移动地面多用户。通过实时更新无人机位置以及动态分配无人机与各个用户通信发射功率，解决由FSO和RF 信道不同引起的速率不匹配问题，最大化混合链路传输速率。

1 系统模型

基于激光微波混合的无人机中继链路系统模型如图1 所示，基站通过FSO 链路将信号传送至无人机中继节点。在中继节点通过光电转换器，将光信号转换为射频信号后通过RF 链路将信号传输至地面移动用户。假设FSO 链路的传输速率大于RF 链路的传输速率，为了使混合链路的速率最大化，需要在满足无人机发射功率最大值条件下对功率进行优化。此外，假定周围环境和信道状态在整个任务执行期间不发生重大的变化，通过当前信道状态迭代计算链路通信速率匹配的位置及各个用户分配的功率，使通信链路整体吞吐量达到最高。按照无人机的管控要求，将无人机高度固定为H=100 m，则无人机坐标为Qu=100)，地面移动用户坐标为QMU=(xu,yu,0)，基站坐标为QBS=(xBS,yBS,0)。

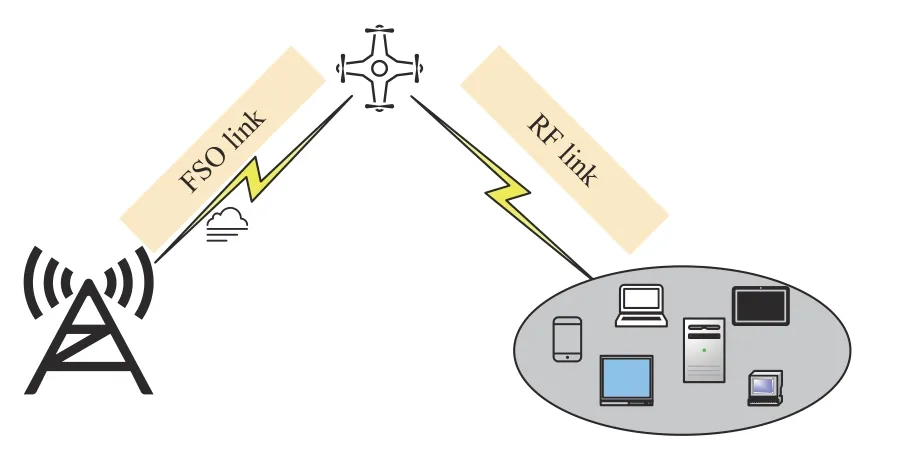
图1 FSO/RF 通信链路系统模型Fig.1 System model of FSO/RF communication link

1.1 自由空间光通信（FSO）模型

在LoS 的无线光通信链路中，指向误差会对系统性能造成一定的影响，对接收光功率造成影响，关于链路中的指向误差对通信的影响，采用如图2所示模型[19]。

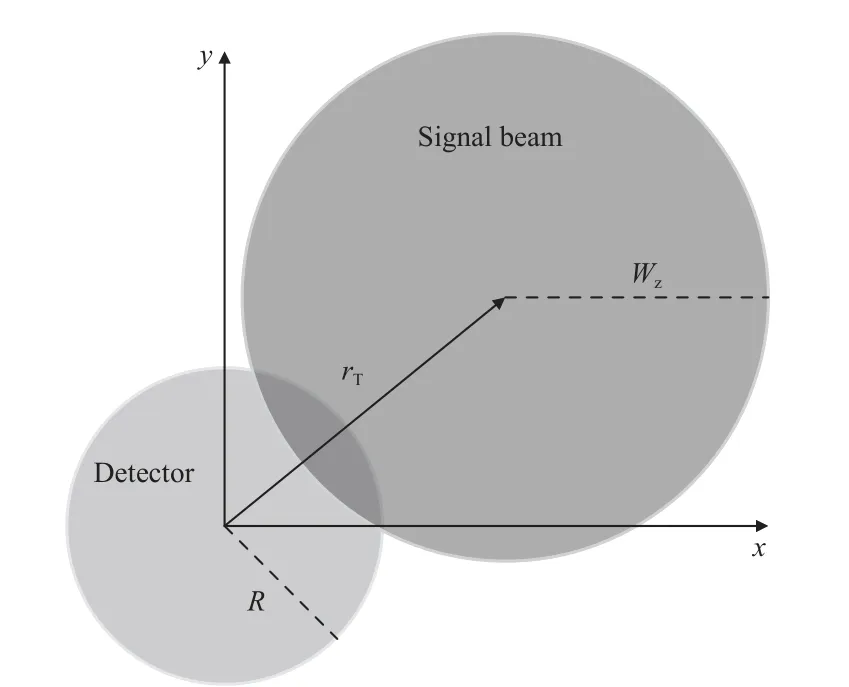
图2 探测器与信号光在接收端处光束偏移示意图Fig.2 Schematic diagram of beam offset between detector and signal light at receiving end

指向误差影响下接收端处信号光束中心与探测器中心存在一定的横向偏移rT，造成在探测器平面内接收的光强减小。对于一般的高斯光束，接收端信号光光强横向分布可表示为[20]

式中：r代表径向距离；WZ为等效光斑半径。由于指向误差影响下的信道增益可表示为[19]

结合上式，得到Ip的概率密度函数表达式为[21]

式中ρ=WZ/2σs。

对于FSO 链路本文做出如下假设：1）本文研究内容均在有雾的情况下，忽略信道湍流对信道传输的影响，FSO 链路信号在大气的衰减主要由3 个因素决定，大气分子的散射效应、大气湍流效应以及大气气溶胶对光信号的影响，本文中主要考虑大气气溶胶对光信号的影响，由于雾的衰减与湍流不相关[19]，在发生雾的情况下，发生湍流的可能性很小（特别是在大雾的情况下）；2）本文假设在保证视距通信的情况下指向、捕获以及跟踪算法能够弥补其指向误差对光通信所带来的负面影响。设指向、捕获以及跟踪算法对于信道增益的影响为hAPT，则假设hp·hAPT=1。那么，无人机中继节点收到的信息表示为[21]

式中：nS,R是加性高斯白噪声，其均值为0，方差为hS,R是自由空间光通信链路的信道增益，根据Beer-Lambert 定理[22]，其可以表示为

式中：dS,R是源节点和中继节点之间的距离；ηdb=3.91(λ/550)-q/V，λ表示波长，V是环境能见度，主要受大气中气溶胶影响；η=ηdbln10/104。粒度分布参数q由Kim 模型[22]公式确定，此模型主要由波长所决定，衰减随着颗粒的波长从0.69 μm至1.55 μm 的增长而增加。

µ*是一个自由变量，用规定范围内的峰值功率和平均功率表示所述信道的容量。α=Pa/Pp，表示其峰均比（average-to-peak ratio,APR），其中光信号平均功率为Pa，峰值功率为Pp。用峰值功率和平均功率表示所述信道的容量，表示如下[23]：

在式（8）中选择输入分布Q来找到容量的下界。为了得到一个逼近的边界，需选择一个与容量相当接近的互信息。这样的分布很难选择，通过使用熵功率不等式(entropy power inequality,EPI)可以规避这个问题。对于任意选择的Q分布，概率密度函数(probability density function,PDF)的概率分布，有下列关系[23]：

为了使这个下界尽可能逼近，需要选择一个分布Q，使得其在给定约束条件下能够使微分熵最大化。为求出光通信信道传输速率的下界，在非负约束、峰值功率约束和平均功率约束下，使微分熵最大化的输入分布PDF 为[23]

为满足平均功率限制条件，µ*为式子α=1/µ*-e-µ*/(1-e-µ*)的解，易知其解总是存在且唯一。从而可得，当0 ＜α ＜1/2时，信道容量下界[24]为

按照上述分析，得出[17]：

湍流对光通信所造成的影响，根据确定参数的不同，现有的光强闪烁模型可以分为单参数模型，双参数模型和多参数模型[25]。单参数模型常用的为对数正态（Lognormal）模型和负指数（Negative Exponential）模型；双参数模型较常使用的是Gamma-Gamma 模型和Lognormal-Rician 模型；多参数模型较为常用的是Málaga 模型。参数的多少主要影响对大尺度涡旋和小尺度涡旋的拟合程度，理论上参数越多对信道的估计越准确，但往往也会带来复杂度提高的问题。由于无雾情况下采用的链路模型不同，因此整个链路通信速率需要加入湍流的影响。本文中未进行无雾条件下的分析，后期将作为研究重点。

1.2 射频通信信道模型

无人机中继节点通过RF 链路发射信号，在用户终端处接收的信息可表示为

式中：xR,D为无人机转发信号；nR,D为方差为均值为0 的加性高斯白噪声；hR,D为射频通信链路的信道增益，其表达式为[26]

式中：τR,D为大尺度衰减影响因子；gR,D为小尺度衰落影响因子，且=1。无人机作为中继节点将接收到的光信号转换为射频信号并传输给终端用户，无人机与终端用户之间的距离为dR,D。按照是否为LoS 链路得到接收信号功率[27]为

式中：αR,D是射频链路的路径衰减系数；φ是由于NLoS链路所产生的额外衰减系数；β指的是在参考距离为1 m 时终端用户收到信号功率。信道视距链路概率可表示为[10]

式中C和B是固定参数，主要取决于环境[9]。无人机高度为H，θ=180/πarcsin(H/du,i)。Ω=P(LoS)×PLLoS+P(NLoS)×PLNLoS，又因P(NLoS)=1-P(LoS)，则由式τR,D可知，信道为LoS 链路总概率为

则信道增益的二阶矩可以表示为[10]

假设无人机发射功率为PU，则射频通信链路通信速率为[10]

2 问题求解

2.1 算法求解

按照所建立的通信模型，考虑下行链路，无人机与用户之间传输速率始终小于基站与无人机之间传输速率，问题转换为优化参数使得无人机与各个用户之间传输总速率最大。设地面移动用户集合为N={1,2,···,N}，ri为无人机与第i个移动用户之间的通信速率，pu,i表示分配给第i个用户的无人机发射功率，i∈N。BFSO为FSO链路的带宽，BRF为RF 链路的带宽，无人机的最大发射总功率为所需优化模型可以表述为

由于无人机位置对信道增益有影响，进而会影响到无人机的发射功率，即各个变量之间有着高耦合的关系，求出全局最优解仍然困难。

2.2 发射功率固定时无人机位置优化

本节求解发射功率固定时无人机的位置优化子问题，此时的无人机传输功率是固定的，问题为求出无人机的最佳位置，使链路吞吐量达到最大。

由于式（23b）和式（23c）仍然为非凸的限制条件，利用连续凸逼近（successive convex approximation，SCA）方法来进行迭代求解[11]。

则将限制条件（23b）转换为（25）的形式，则非凸的无人机位置坐标优化问题可以转换为下述第t次迭代的凸规划：

2.3 无人机位置固定时的发射功率优化

本节求解无人机位置固定时的发射功率优化子问题，此时无人机的位置坐标是固定的。此子问题也可以当成是一些特殊任务的场景，例如进行某一固定区域的监视行动或者地面用户固定的场景。

对于限制条件式（21b），可以利用拉格朗日乘数法[28]进行求解，乘子为 α，即：

设传输功率优化的对偶问题为g(ρ)，{pi,u(ρ),Ri(ρ)}是对偶问题的最优解。注意此处的ρ ≤1，否则当Ri→-∞时，g(ρ)无下界。假设 ρ*是最优的对偶解，功率优化子问题的最优解{pi,u(ρ*),Ri(ρ*)}的求解需要考虑两种情况：

1）当0 ≤ρ*＜1，在满足KKT 条件的情况下利用注水定理[11]得到最优解为

2）当ρ*=1，根据互补松弛条件，可以推断出满足限制条件(21b)，因此有：

在这种情况下，传输速率主要由基站到UAV之间的速率所决定。当ρ*=0时，如果不能满足条件式(21b)，则可以通过减少无人机的传输功率来满足此条件，即限制无人机到用户之间的速率。

2.4 无人机的坐标和传输功率的联合优化

表1 算法流程Table 1 Flow of algorithm

3 仿真结果

3.1 参数设置

为保证无人机飞行轨迹更加易于观察，设置地面用户以[2 500,0,0]为圆心，作半径为500 m 的圆周运动。参数设置如表2 所示。

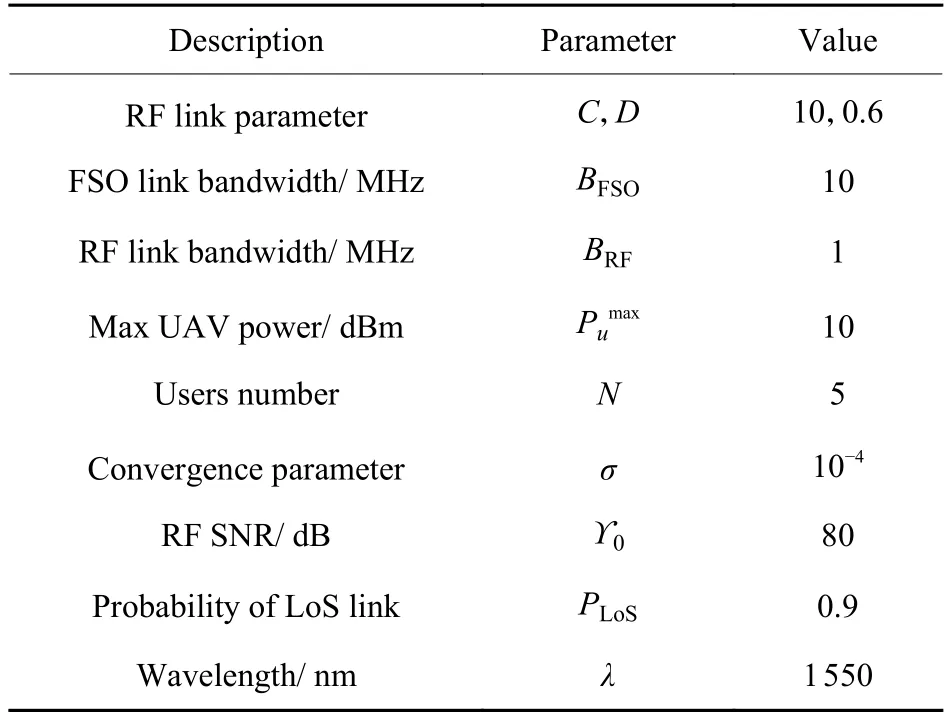
表2 参数设置Table 2 Parameters setting

3.2 不同参数下的系统传输速率

仿真过程中，注意到无人机初始值的设置能有效减少迭代的次数。本文在轨迹开始优化时，根据用户中心与基站之间的距离先大致算出两者速率匹配时的距离，则无人机快速飞至指定位置，开始无人机轨迹的优化迭代。本文根据仿真结果优化了初始值的设置，仿真结果证明，比直接飞至用户上空能够平均减少位置优化迭代次数5 次。能见度的选取根据公式（7）不同的能见度标准进行选取，由于本文主要考虑在轻雾的情况下，因此能见度选取时集中于能见度较低的情形。同时为了便于对比，分别选取能见度0.5 km、1.0 km、1.4 km和1.7 km 4 种情况进行对比。

图3、图4 设置FSO 链路能见度为1.0 km。图3 为无人机和地面用户运动轨迹俯视图，图4 为混合链路传输速率与无人机距离基站距离对比图。由图3 可知，在所设置信道参数条件下，无人机跟随地面移动用户作近似圆周运动，即跟随无人机轨迹在其内侧运动。图4 为无人机距基站距离与通信速率的对比图，易知两者呈负相关关系，即随着距离的增大混合链路通信速率降低。无人机运动在靠近用户一侧，根据FSO 和RF 之间信道不匹配情况，此时链路FSO 链路速率能够满足RF 链路全速传输，链路总体通信速率的提升主要受制于RF 信道的通信速率。

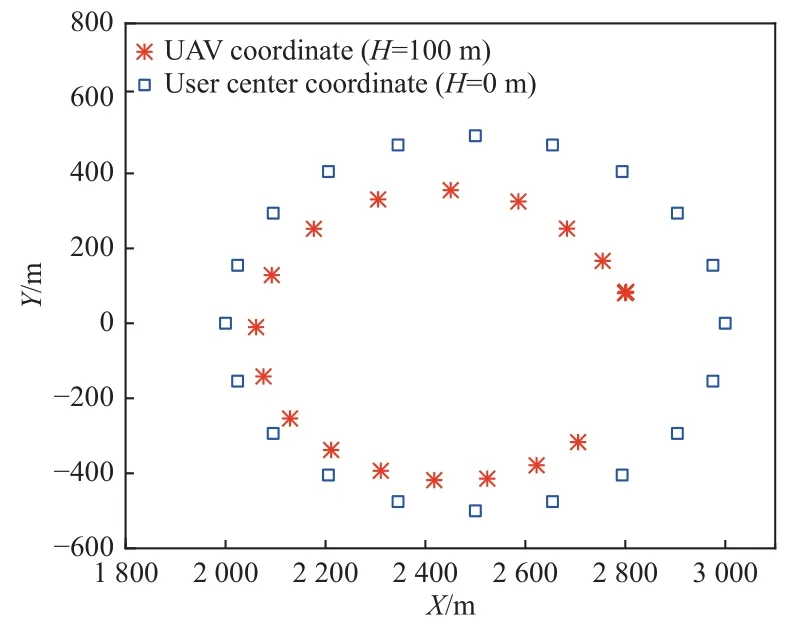
图3 无人机和地面用户运动轨迹俯视图（能见度1.0 km）Fig.3 Top view of motion trajectories of UAV and ground user (with visibility of 1.0 km)

图4 传输速率与无人机-基站距离对比图（能见度1.0 km）Fig.4 Comparison of transmit rate and distance between UAV and base station (with visibility of 1.0 km)

图5、图6 设置FSO 链路能见度为1.4 km。图5中，无人机在俯视图中轨迹基本与地面移动用户的轨迹重合。分析可知此时无人机基本上在地面移动用户中心上空，随着与基站距离的减少，FSO 链路的速率增大，链路总体速率得到提升。图6 中间一段链路整体传输速率随无人机离基站距离增大并未出现明显增长。分析可知在距离降低到一定程度后RF 链路传输速率的限制达到瓶颈。此时无人机与用户之间距离近似等于其高度，无法继续减小，链路整体速率也基本维持原速度。

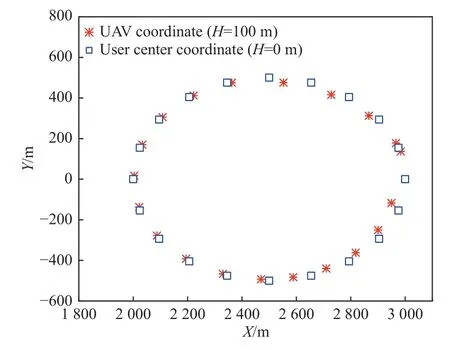
图5 无人机和地面用户运动轨迹俯视图（能见度1.4 km）Fig.5 Top view of motion trajectories of UAV and ground user (with visibility of 1.4 km)

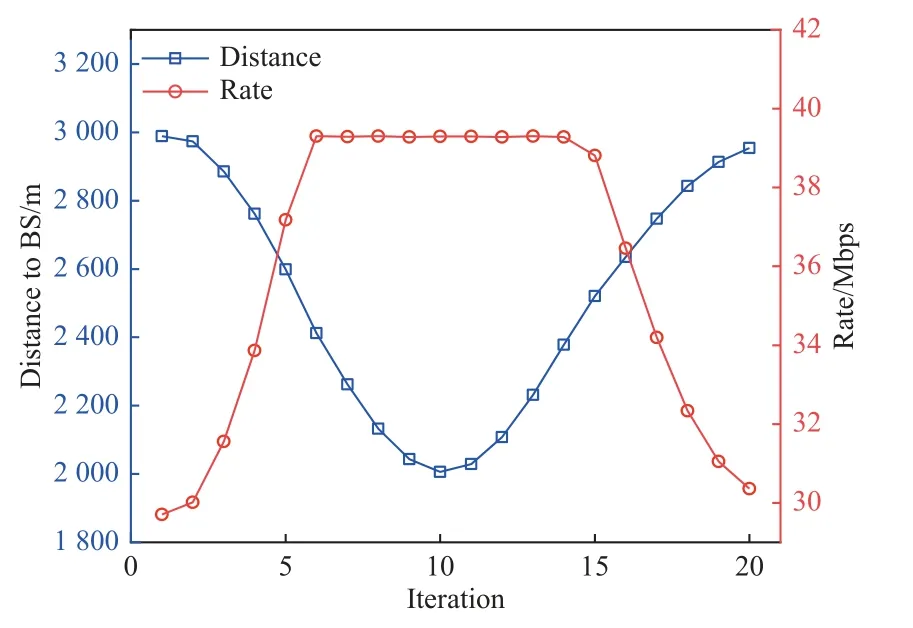
图6 传输速率与无人机-基站距离对比图（能见度1.4 km）Fig.6 Comparison of transmit rate and distance between UAV and base station (with visibility of 1.4 km)

图7、图8 设置光通信信道的能见度0.5 km。由图7 可知，此时无人机并未随着地面移动用户的移动而移动，而是固定在1 550 m 左右，其混合链路速率也并未随着地面用户距离的接近而出现明显增加。由此可得出结论，在此种链路参数下，移动用户的运动并非是通信速率提升的关键，此时混合链路的速率主要由光链路决定，即光链路在超过此距离时光通信速率会急速下降，在此距离区间内速率接近射频链路的传输速率，导致混合链路的速率达到一个动态的平衡，即此时混合链路的速率主要由光通信的速率所决定。由图8 对FSO 链路仿真可知，在对应参数设置下，距离超过1 550 m时，光链路的通信速率接近0，符合轨迹优化链路的仿真结果。

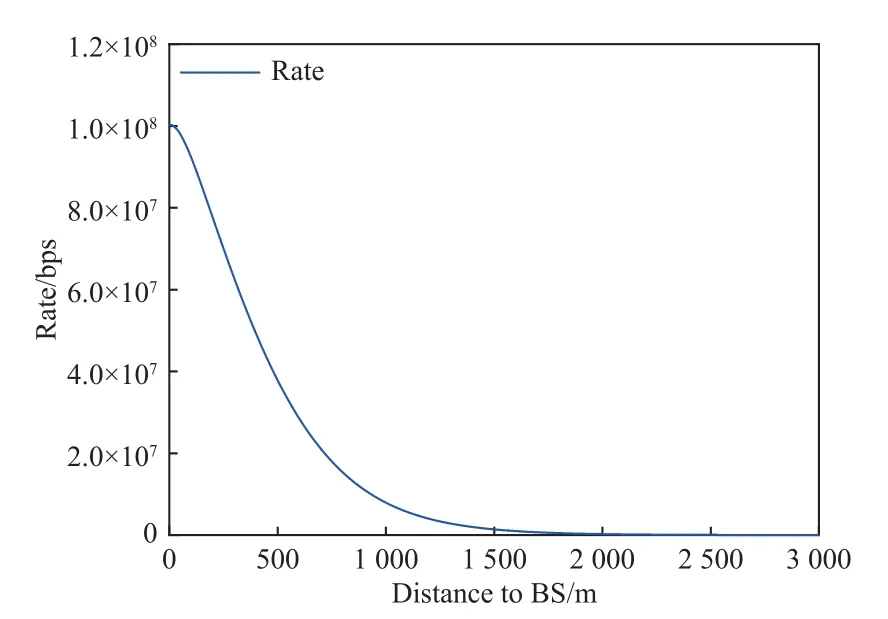
图8 FSO 信道传输速率随无人机距离变化图（能见度0.5 km）Fig.8 FSO channel transmission rate varies with UAV distance (with visibility of 0.5 km)

图9、图10 设置光通信信道的能见度1.7 km。由图9 可知此时无人机的轨迹基本完全在地面移动用户的上方，这意味着此时混合信道的速率完全取决于射频信道的通信速率。由图10 可知，混合信道的通信速率没有较大变化，稳定在平均值39.2 Mbps 附近，此时RF 信道链路速率已达其瓶颈值。

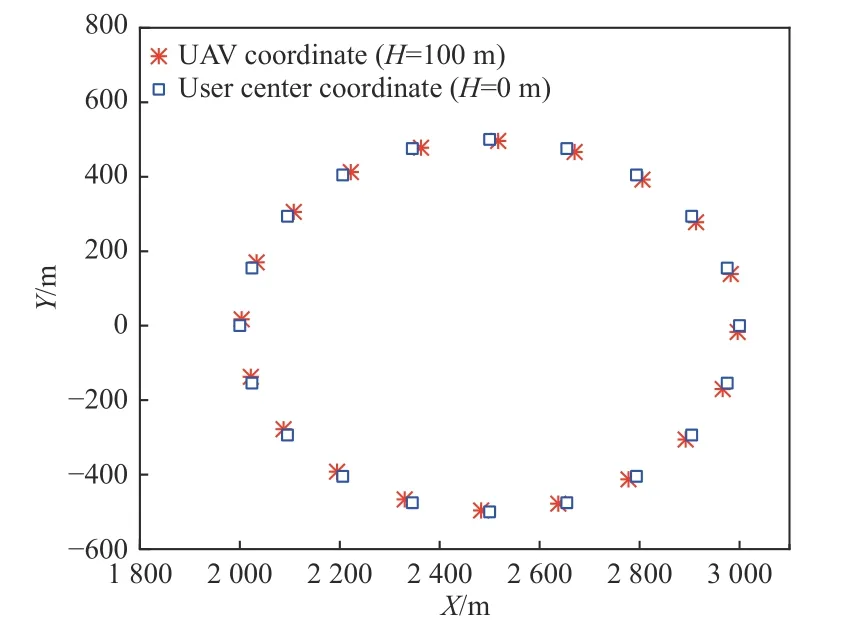
图9 无人机和地面用户运动轨迹俯视图（能见度1.7 km）Fig.9 Top view of motion trajectories of UAV and ground user (with visibility of 1.7 km)

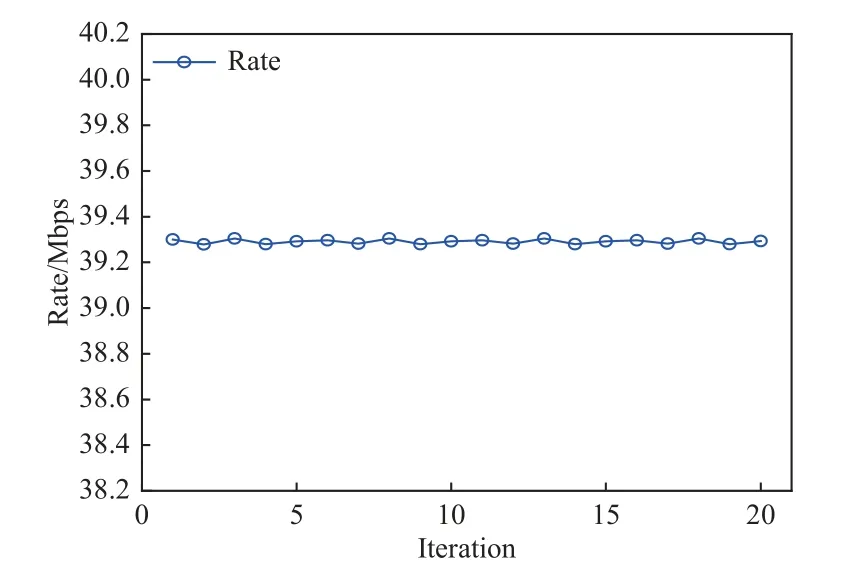
图10 混合信道通信速率（能见度1.7 km）Fig.10 Mixed channel communication rate (with visibility of 1.7 km)

设置不同RF 信道带宽及无人机发射功率，由图11 易知均会对混合链路收敛结果产生影响。提高RF 链路总带宽后以及无人机的总发射功率后，混合链路的传输速率均得到了提升。图12 为3 种方案的对比，可以得出，所提算法能够有效提升链路整体传输速率。根据所建模型，在能见度为1.0 km的情况下仿真3 种方案：方案1 为所提算法，对无人机位置坐标及功率进行联合迭代优化，并对其进行实时更新；方案2 对无人机位置进行了优化，无人机飞行至地面移动用户中心的正上方并随之移动，但未针对与各个用户之间距离对无人机发射功率进行优化；方案3 为固定式无人机中继，即无人机悬停至固定位置，其坐标为(2 500,0,0)，也未对无人机发射功率进行优化。

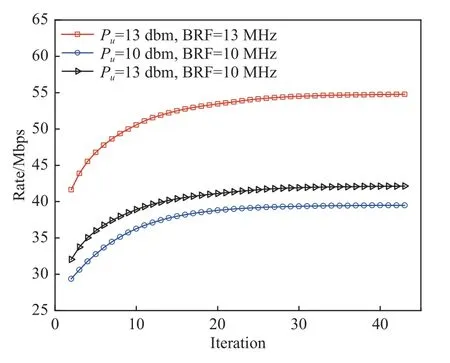
图11 不同带宽及无人机发射功率设置下收敛图Fig.11 Convergence diagram under different bandwidths and UAV transmission power settings

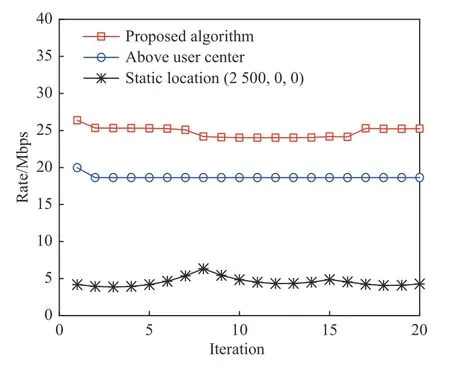
图12 所提3 种方案对比图Fig.12 Comparison of three proposed schemes

根据表3 可知，随着能见度的提高，链路平均传输速率也在逐渐增加。当逐渐达到射频传输链路的上限以后，其增长逐渐减慢直至停止。所提算法能够有效解决有雾条件下光链路信道质量不佳的问题，通过轨迹优化及发射功率优化实现尽可能发挥两端链路的性能，从而使链路的整体传输速率得到提升。

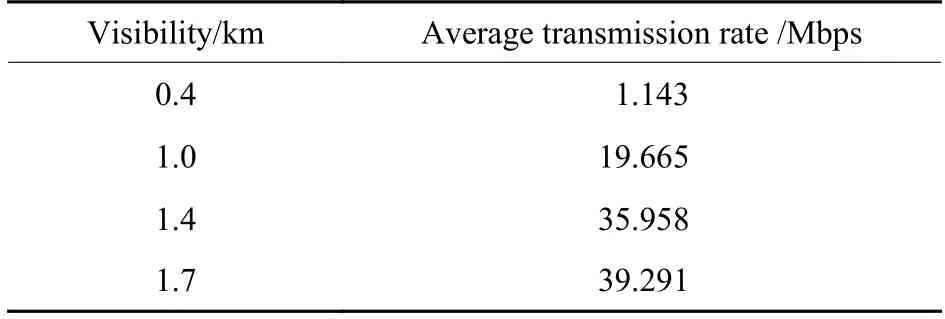
表3 不同能见度下平均传输速率Table 3 Average transmission rate under different visibility

4 结论

本文通过设置不同的FSO 链路参数，分析FSO/RF 链路达到速率匹配的距离及速率等参数。结果表明：在FSO 链路能见度为1.0 km时，混合链路速率主要受RF 链路信道容量限制，随着RF 链路信道容量的增长而增长；能见度为1.4 km时，仍然随RF 链路信道容量的增加而增加，但受无人机发射总功率影响，信道容量有一段瓶颈期；能见度为0.5 km时，混合链路速率主要受FSO 链路信道限制，随着FSO 信道容量的增长而增长；能见度为1.7 km时，FSO 链路和RF 链路均已达到其信道容量，无法通过轨迹优化使信道容量得到有效提升。设置不同RF 链路参数仿真与上述过程类似。仿真结果表明，所提出的算法能够快速迭代达到收敛条件，满足用户基本通信需求。相较于固定式中继，链路总体传输速率得到了447%的提升，说明无人机机动方案非常必要。同时对无人机发射功率进行优化后的链路平均传输速率相较于未优化方案有了32.54%的提升，特别是在用户之间分布不均匀的时候表现较为明显，证明了算法的必要性。所提算法为保证RF/FSO 链路的高速传输及可靠通信提供了可供参考的解决方案。所提模型可应用于例如演唱会等集会、突发军事行动等场景，无人机作为一个移动的空中平台，充当地面基站的角色。利用光通信的大带宽与无人机之间进行大容量数据传输，利用射频通信的灵活接入的特点，满足多设备同时接入的需求。