永磁直驱风电场故障等值建模方法
2023-09-21张武洋杨飞孔繁哲刘梦夏田景辅贾科毕天姝
张武洋,杨飞,孔繁哲,刘梦夏,田景辅,贾科,毕天姝
(1. 国网辽宁省电力有限公司电力科学研究院,沈阳 110006;2. 国网辽宁省电力有限公司,沈阳 110006;3. 新能源电力系统国家重点实验室(华北电力大学),北京 102206)
0 引言
随着规模化风电、光伏集中并网,新能源高占比系统的故障特征发生根本改变。单个场站通常包含大量的风机和光伏阵列,这导致网络节点数大量增加,使得网络短路电流计算量显著增加,甚至结果不收敛[1]。现有的传统单机等值模型难以精确反应新能源场站的故障特征,因此亟待研究准确的新能源场站故障等值建模方法。
目前针对新能源场站故障等值建模的研究可以分为单机等值法[2-5]和多机等值法[6],研究表明多机等值建模方法能够更准确反映场站的故障特征。
多机等值建模方法的分群指标根据是否含有明确的分群边界,主要分为离散型变量和连续型变量两类分群指标。其中采用离散型变量指标的分群方法包括:根据正常运行时的风机控制方式[6]、故障后的低穿控制方式[7-8]或按照故障区域进行机组划分[9],这类指标含有明确的分群边界,分群指标为控制方式或者故障区域,其指标采集难度较低,但在机组采用相同控制方式的情况下,其等值模型的误差不能保证,等值方法精度较低。
采用连续型变量指标分群方法多利用电气量进行分群,基于聚类算法或智能算法的等值建模方法被广泛采用,分群指标主要分为稳态变量和暂态变量两类。其中采用稳态变量指标的分群方法包括:风机稳态运行时的转速[10]、风速[11-12]、功率[13],或正常运行时的多个风机变量[14]等指标。这类方法所选取的聚类指标为稳态量,难以反映系统的动态过程,对于暂态过程等值精度较低,但分群指标易于采集、易于实现,等值方法效率较高。
对于采用暂态变量指标的分群方法,电网发生故障后,根据逆变型电源的故障特性的影响因素,文献[15]将控制参数的灵敏度作为分群指标进行分群等值。文献[16-21]将多电气量暂态响应特征作为风电机组的分群依据。文献[22]基于哈密顿作用,提取多个状态变量的特征量对机组进行分群等值。这类方法能够全面反映机组间的全时间尺度的故障特征差异,其暂态等值精度较高,但这类方法所需分群指标为暂态量,需要对场站的详细模型进行大量暂态计算,指标采集难度高,分群方法效率较低。
大多采用连续型变量作为分群指标的等值方法,存在的核心问题是分群边界不清,分群数依赖于算法中所预设的参数;所得等值模型与详细模型之间未建立有效的误差联系,等值结果的优劣只能通过仿真验证。
基于上述问题,本文构建了永磁风电场等值前后输出的故障电流关系,并根据等值建模所产生的短路电流误差与电气量边界的解析关系,确定了场站分群等值建模的电气量边界,解决了分群边界整定的问题。最后在PSCAD 中建立了仿真模型,通过比较本文所提等值模型与单机模型的故障电流,本文所提方法精度提高了约4%,相比传统故障稳态聚类算法误差平均降低了约1.7%,证明了等值模型的准确性和适用性。
1 永磁风电场的详细模型
本文以现场实际典型的永磁直驱风电场为例进行等值建模分析。风电场采用如图 1 所示场站拓扑结构,场站包括永磁直驱风机、背靠背换流器、箱变(0.69 kV/35 kV)和主变(35 kV/220 kV)。
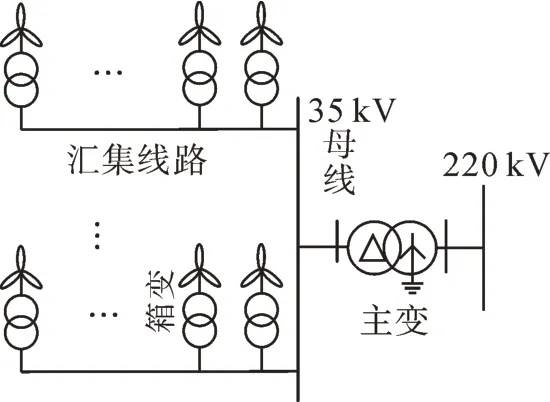
图1 风电场详细模型示意图Fig 1 Sketch diagram of the detailed wind farm model
1.1 场站的拓扑结构
场站的网侧换流器(grid side converter,GSC)采用电压电流双闭环控制,正常运行时,电流dq轴分量指令值由电压外环给出;故障后外环切除进入低穿控制,此时电流指令值直接给定。根据瞬时无功功率理论,可以得到逆变器的输出功率为:
式中:P、Q分别为GSC 输出的有功功率和无功功率;ud、uq分别为GSC出口dq轴电压;id、iq分别为GSC输出的dq轴电流。
风机的有功功率可以根据风速计算得到:
式中:ρ为空气密度;R为风轮机半径;vw为风机输入风速;Cp为风能利用系数,同时场站的输入风速需要考虑尾流效应的影响[12]。
根据永磁风机低穿控制国家标准[23],故障期间电压跌落大于0.2 p.u.,场站进入低穿控制。可以得到永磁风机故障后不同控制模式下输出的dq轴短路电流[23]。
式中:IN为机组的额定电流;Im为GSC 输出电流限幅值。
1.2 多机短路电流相位归算
由于机组故障后的电流dq轴分量基于GSC 出口电压相位进行分解得到,各个机组的相位均不相同,因此需要将各机组的相位换算至同一参考系,选择系统中的同步机相位作为参考系进行相位的换算[24]。将等值前的详细模型短路电流dq轴分量归算至参考电压相位可以得到式(5)。
式中:idΣ、iqΣ分别为详细模型归算至参考电压相位的电流dq轴分量;idi、iqi分别为机组i按各自机端电压相位输出电流的dq轴分量;θi为机组i机端电压相位和参考电压相位的差值。
同理对于分群等值建模后的等值模型有:
式中:idΣeq、iqΣeq分别为等值模型归算到参考电压相位的短路电流dq轴分量;ideq、iqeq分别为等值机组在机端电压相位参考系下输出电流的dq轴分量;θeq为等值机组机端电压相位和参考电压相位的差值。
根据式(3)、式(5)永磁风机在故障后呈现压控电流源的特性,其故障特征由电流控制方式、电压跌落程度、故障前所发有功功率(风速)与锁相环输出相位即机端电压相位决定。
2 等值方法
2.1 逆变型电源等值总体思路
本文所提场站等值模型为保护整定计算、短路计算所用,因此忽略故障过程中的机械部分动态过程。由于不同的控制模式下永磁同步发电机(permanent magnet synchronous generator, PMSG)的故障电流故障特征不一致,因此首先将机组按照是否进入低穿控制分为两类。
其次根据机组的电气量进一步分类,对于划分为同一类的机组,对机组的电压进行等效,根据等效电压计算线路等值阻抗,实现对集电线路的等值。
本节首先推导两台机的等值误差与电气量边界的解析关系,再进一步分析多机的等值误差与电气量差异的关系,等值后的场站拓扑如图 2所示。
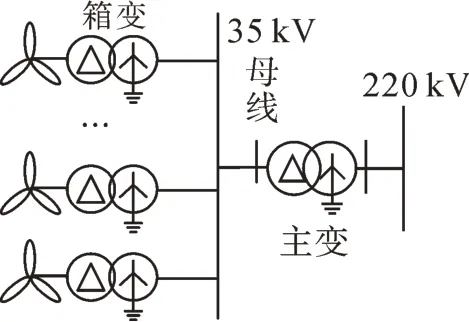
图2 等值风电场站拓扑图Fig 2 Topology diagram of equivalent wind farm
多机等值模型的参数计算公式分别为:
式中:Seqi为等值机组i的容量;Si为风机i的容量;Ni为分为群i的风机数量;STeqi为等值模型变压器i的容量;STi为各变压器容量;xTeq为等值模型的变压器电抗;xTi为机组变压器i的电抗;vweq为等值机组i的风速;vwi为机组i的风速。
2.2 进入低穿控制
当电压跌落程度较深时,永磁风机进入低穿控制,联立式(3)与式(5)可以得到:
式中Im1、Im2分别为两逆变器的电流限幅值;φi=arctan(idi/iqi)。
化简可以得到:
其中:
同理可以得到等值机组的短路电流为:
式中φeq为等值dq轴电流相角。
比较式(9)和式(11),可知等值带来的dq轴电流误差由两部分组成:1)由于等值机组以容量不变、控制参数不变为原则进行等值,因此电流限幅值为等值前的机组限幅值相加,为Im1+Im2,但详细模型输出电流则为各机组输出电流的矢量和,电流的幅值小于Im1+Im2,可见其带来的dq轴电流幅值项误差无法避免。2)由于电压幅值及相位不同带来的余弦项误差,即θeq+φeq与θ1+φ1+α的差异,该差异可以通过对电压等效消除,因此等值带来的短路电流误差主要为上式中的幅值项。
2.2.1 等值阻抗计算
当场站送出线路发生故障时,令θeq+φeq=θ1+φ1+α,用以消除电压相位差产生的余弦项误差,此时等值前后的电流相位相等,基于前文假设,则有等值前后的功率因数相等,忽略线路上的功率损耗,可以得到:
式中Imax为最大电流限幅值。
联立式(1)、式(3)和式(12),求解等效电压Ueq,并保持线路阻抗角不变,根据下式计算等值线路长度。
式中:Peq、Qeq为等值后逆变器输出的功率,根据式(1)得出;XT为等值变压器电抗;r、x分别为线路的单位电阻和电抗;Upcc为并网点电压幅值;ΔU、δU分别为电压降落的纵分量和横分量;l为等值线路长度 。
2.2.2 等值聚合边界
根据前文的分析,等值带来的幅值项误差无法避免,因此通过推导等值产生的电流误差与电气量边界关系,根据所得电气量边界实现分群。
式(11)减去式(9)可以得到等值误差。
由于各风机出口电压跌落程度相近,因此δ较小,故对上式进行线性化,泰勒展开并忽略高阶项可以得到:
定义等值产生的相对误差为:
由式(16)可推导得出:
上式中的余弦项误差通过电压等效进行消除,因此式(17)第2 项为1,可以得到等值产生的相对误差为:
根据式(18),对进入低穿控制的风电场进行等值,产生的故障电流误差主要由各风电机组的电流限幅值、有功功率、各风电场出口电压幅值及相位决定。
2.3 等值方法推广至多机
上节得到了两台机组等值误差与电气量边界的关系如式(18)所示,对于多台机组等值误差与电气量边界的关系推导如下。
先对分为一类的机组中的两台机组进行等值,将第一步得到的等值机组再与下一台机组进行等值,那么对于含有N台机组的场站,需要进行N-1次等值计算。根据式(18)中dq轴电流等值误差形式一致,对于两台机组等值产生的dq轴电流误差,考虑误差最大的情况有:
式中:δij=(θi+φi)-(θj+φj)为分为同群中的相角差最大值,可以进一步得到的等值机组输出的短路电流为:
式中:N为场站机组数量;idq1为机组1 的dq轴电流;idq2为机组2的dq轴电流;idqi为机组i的dq轴电流;ε1为将机组1、2 等值带来的误差;εi为将等值机组i与下一个机组等值带来的误差。由式(19)可知,在等值过程中,在进行第i次等值过程中,δij始终小于归为一类机组中两机组的最大值δmax,误差如式(21)所示。
式中:idqΣ为详细模型归算至参考电压相位的dq轴电流;idqeq为等值机组输出的dq轴电流;ε0为对同群内电气量差值最大的两机组等值产生的误差。对上式进行放缩可以得到多机等值误差ε与分为同类机组的电气量差异最大值δmax的关系为:
根据上式可以设置等值误差上限以计算电气量边界,若两机组的电气量差异δij小于通过得到的电气量边界上限δmax则分为同一类,否则分为不同类。至此,本节建立了多机等值误差与机组电气量差异边界的关系,实现了机组分群等值。
3 仿真验证和结果分析
为验证本文所提方法的可行性,以内蒙典型风电场为例,在PSCAD 中搭建了如图 1 所示详细模型,风场规模为50 台机组。风电场参数如附录A中表A1所示,机组间距选为1 km[25],考虑风电场中风速分布受尾流效应影响,基本风速设置为8 m/s。
以送出线路10 km 发生故障为例进行仿真验证,选取两种典型的工况:电压跌落至30%、50%进行结果分析。为证明所提等值建模方法优越性,将本文所提方法与单机模型以及现有的两种等值建模方法进行了仿真验证结果的比对,模型一:以电压及功率故障稳态量作为分群指标,模型二:以电压及功率故障暂态量作为分群指标。分群算法采用k-means 聚类算法,分群数量整定为2 群,阻抗等值方法均采用加权平均电压法。仿真硬件条件如下,处理器为: Intel(R) Core(TM) i7-7700HQ CPU@2.80 GHz,机带RAM:16 GB,SSD:TOSHIBA THNSNJ128G8NY 128 GB。
因此其余不同的电压跌落程度及风速下的仿真结果如附录表A2、A3所示。
3.1 并网点电压跌落50%
当并网点电压跌落50%时,风电场内全部机组进入低穿控制,此时根据所需精度及式(18)设置误差上限,并求解此时的电气量边界,本文在不同电压跌落程度下均设置为ε0=0.05%。根据机组的机端电压及功率进行分群,得到的分群结果如表 1所示。
风电场采用单机等值模型、传统聚类算法所得等值模型与本文所提等值模型等值前后产生的短路电流波形及误差如图 3、表2所示。
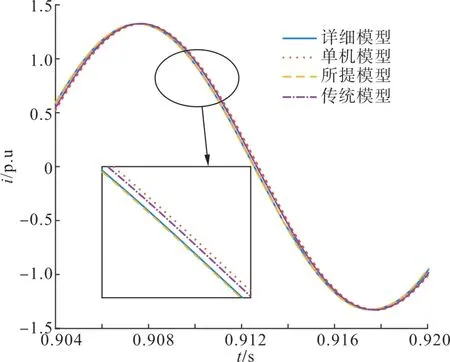
图3 短路电流波形对比Fig 3 Short circuit current waveform comparison
根据式(22)及设置的误差限可以得到风电场等值的理论误差为1.9%,仿真结果dq轴电流均小于理论误差限。相比单机等值模型,本文所提方法的短路电流dq轴分量误差平均降低了3.82%,相比传统聚类算法误差平均降低了2.35%,在保证模型精度的前提下,一定程度上简化了模型的复杂度。
由表2 可知,各类方法的分群算法所需时长均较短,建立等值模型所需时长主要取决于等值模型的仿真时长及分群数据的计算时长。对于分群数据计算时长,模型一采用故障稳态数据,计算时长较短,分群效率较高。模型二采用故障暂态数据,其计算时长较长,分群效率相对较低。
3.2 并网点电压跌落30%
当并网点电压跌落30%时,采取与前文相同的等值方法进行等值,分群结果如表 3所示。
风电场采用单机等值模型、传统聚类算法所得等值模型与本文所提等值模型等值前后产生的短路电流波形及误差如图 4、表 4所示。
根据仿真结果,相比单机等值模型,本文所提方法的短路电流dq轴分量误差平均降低了3.04%,相比传统聚类算法所得等值模型,误差平均降低了1.49%。
对比表2、表 4,其中模型仿真时长主要由等值模型所含机组个数决定。考虑50 台风电机组的算例,分群数量在3 群以内时,本文所提方法分群算法所需平均计算时长及分群数据计算时长均在2 s以内,保证了较高的分群效率。
其余电压跌落程度及不同风速下的仿真结果如附录A 中表1、表2 所示,根据设置的误差上限对不同电压跌落程度下的风电场进行了多机等值,可以看到,由于电压跌落程度较深,风机输出的功率较小,因此风机间的电压差异较小,所以随着电压跌落程度的加深,由于设置误差限相同,因此本文所提方法的分群数量随着电压差异的减小而减少。所提等值方法与单机等值方法相比,故障电流误差平均降低了约4%,相比传统故障稳态聚类算法误差平均降低了约1.7%。

表1 风电场分群结果Tab. 1 Clustering results of wind farms

表2 工况一各模型计算效率与精度对比Tab. 2 Comparison of calculation efficiency and accuracy of each model under condition 1

表3 风电场分群结果Tab. 3 Clustering results of wind farms

表4 工况二各模型计算效率与精度对比Tab. 4 Comparison of calculation efficiency and accuracy of each model under condition 2
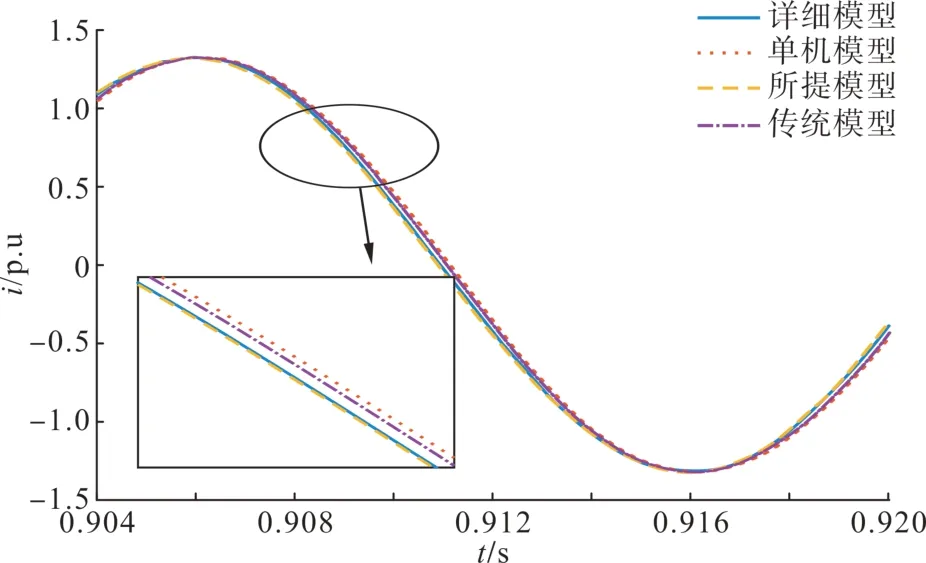
图4 短路电流波形对比Fig 4 Comparison of the short circuit current waveforms
4 结语
针对现有大多依据连续型分群指标的多机等值方法存在的分群边界不清的问题,本文基于PMSG的故障特性,推导了PMSG 多机等值误差与机组电气量的解析关系,并根据所需精度得到多机等值的电气量边界,构建了永磁风电场的等值模型。仿真结果表明本文所提模型相比单机等值模型精度提高了约4%,相比传统故障稳态聚类算法误差平均降低了约1.7%,验证了所提等值建模方法的可行性。
附录
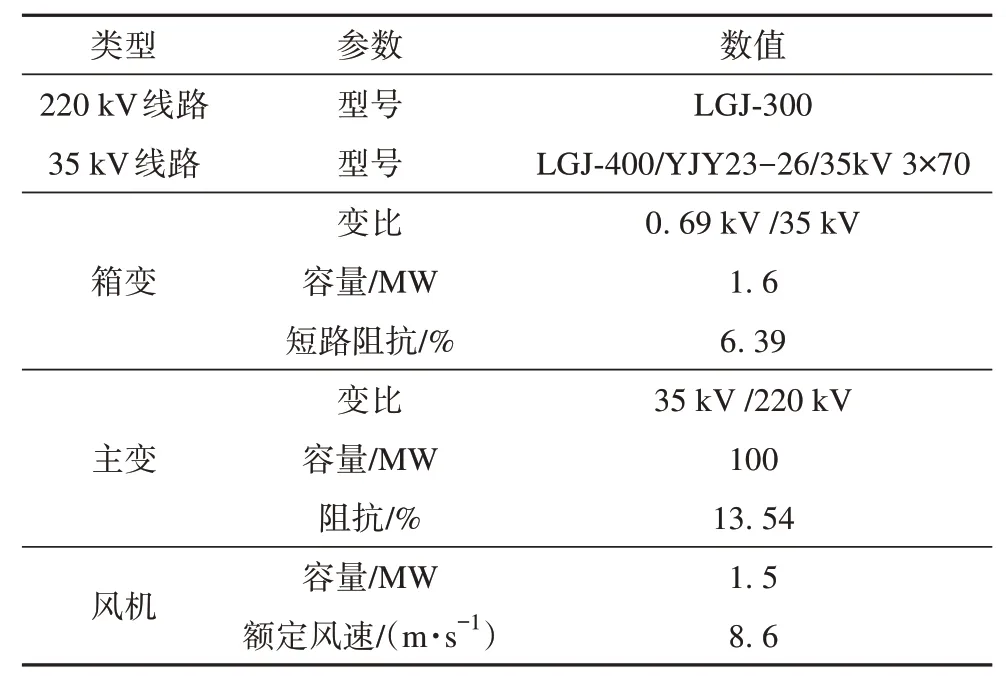
表A1 永磁风电场主要元件参数Tab. A1 Main component parameters of permanent magnet wind field
