钢板大变形热轧机轧制力DEI-RBF预测研究

2023-09-21王保华葛新锋胡草笛

机械设计与制造 2023年9期

王保华，葛新锋，杨波，胡草笛

（1.焦作大学机电工程学院，河南焦作 454000；2.许昌学院工程技术中心，河南许昌 461000；3.河南理工大学机械与动力工程学院，河南焦作 454003）

1 引言

对钢板进行热轧加工的过程容易存在板形结构缺陷而造成产品不合格的情况。当压辊受到不同的轧制力作用时，其弹性变形程度也存在较大差异，之后进一步引起带钢板形尺寸的改变，可以为更好地改善钢板板形提供参考价值［1-5］。

前期大部分学者构建的轧制模型没有为各参量设置合适的耦合关系，模型精度受到实际参数设置条件的显著影响。采用人工智能处理技术不需要对滚动过程的深层规律开展重复性探索的过程，该方法能够根据人脑活动方式的模拟进行事件处理，根据实际信息与参数特征分析数据的具体规律［6-7］。到目前为止已经形成了支持向量机、神经网络、专家系统多种处理技术［8-9］。同时还有学者开发了轧制力控制方面的智能模型，文献［10］根据收集得到的宝钢1880热轧精轧机组数据，相对传统宝钢1880热轧轧制力模型获得了更高的预测精度。文献［11］通过灰色关联实现轧制力分析，可以达到7%以内的预测偏差，实现了预测精度的显著提升，充分满足了现场的实际使用需求。以上文献虽然都能够达到较高预测精度，但容易引起局部最优结果，采用深层神经网络模型能够增强模型泛化性能，模型的训练过程需耗费较长的时间，不能达到快速收敛的效果，从而限制了采用神经网络模型预测轧制力的过程［12］。现阶段，以支持向量机模型进行热轧轧制力预测的文献报道还较少，其中，文献［13］初步构建了以支持向量实现的机轧制力预测模型，表明轧制力预测模可以满足实际应用要求，进一步提升预测精度。

与其它模型相比，支持向量机实际计算过程的复杂性主要由支持向量数决定，从而克服了“维数灾难”，简化了处理过程，可以获得优异鲁棒性，同时精度也获得明显提升。综合运用上述两种处理方式，设计了一种差分进化改进支持向量机模型（DEIRBF），分别测试了线性（Linear）、高斯（RBF）、多项式（Poly）这几种核函数支持向量机的预测性能，并以RBF核函数支持向量机（RBF-SVM）构建初始模型。之后通过差分进化算法完成RBFSVM惩罚系数C以及RBF核函数参数σ的寻优，结果显示，DEIRBF可以实现热轧轧制力的精确预测，从而达到现场使用要求。

2 实验模型

2.1 轧制力SVM模型

选定样本：

经学习构建以下模型：

确保f（x）尽量接近y，w与b属于模型需确定的参数。

计算得到回归模型输出f（x）与实际输出y之间的差值，并由此判断模型损失情况，其中，f（x）=y时，表示损失为0。对不同的容忍偏差条件下分析，满足|f（x）-y|小于0条件时，可以忽略模型的损失，如果满足|f（x）-y|大于0时，则需要进行损失计算。

通过Cortes构建的C-SVC模型，考虑松弛变量以及正则化参数C，可以得到以下的轧制力SVM模型：

以拉格朗日乘子法将其转换成对偶分析问题，再利用SMO方法构建得到轧制力SVM回归模型计算式：

2.2 DEI-RBF算法

对于常规SVM模型，需通过人工方法设置SVM模型的合适参数，由此实现模型预测精度的显著提升。现阶段，尚未有文献报道关于模型参数理论设置方面的内容。通常可以利用经验方法或采用实验测试的方式设置模型参数，但存在耗费较长时间的问题。为实现对模型最优参数的选择，选择群搜索优化算法来实现寻优过程，主要包括粒子群算法与遗传算法。根据以上研究结果，在SVM模型内加入了差分进化算法，建立了一种更加高效的学习算法DEI-RBF。DEI-RBF的具体控制流程，如图1所示。

构建DEI-RBF 模型的时候，可以根据DE 计算合适的SVM模型惩罚系数C以及优化核函数参数σ，由此获得最优的模型参数组合结果，使模型稳定性与准确率都获得提升。

3 实验分析

3.1 建模数据预处理

对某钢厂的2250 热轧产线中提取得到的共3000 组样本参数，如表1所示。为提升模型准确率并更快完成优化计算，对各项数据按照以下方式实施归一化。

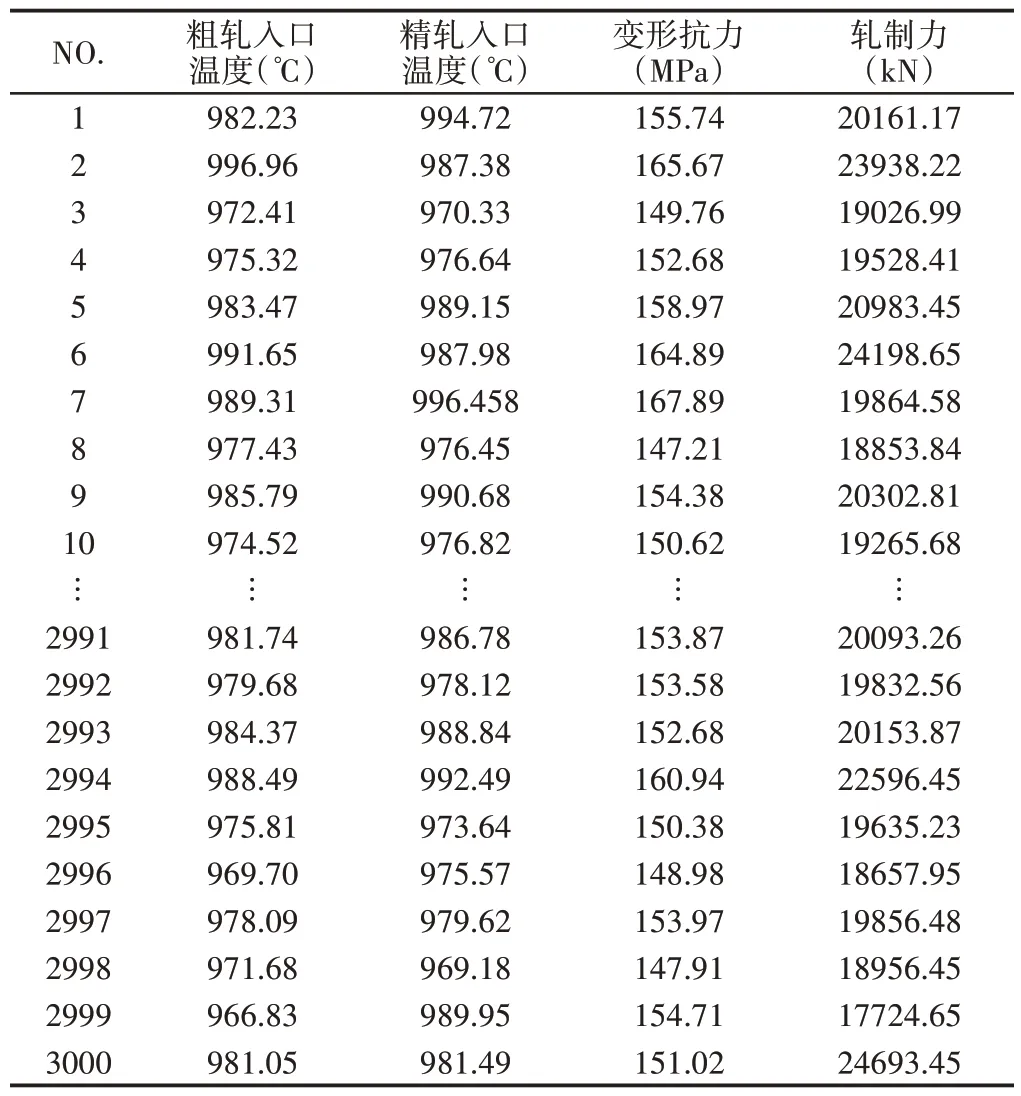
表1 测试数据（部分）Tab.1 Test Data（Part）

3.2 结果分析

分别以Linear、Poly与RBF核函数构建相应的支持向量机回归模型，对比不同核函数模型得到的处理结果准确率与误差。输入参数包括粗轧入口与出口温度、中间坯厚度与宽度尺寸、轧辊半径、变形抗力、精轧的出口厚度与宽度尺寸、精轧入口与出口温度以及C、P、SI、S各项特征参数，变形抗力则通过系统变形抗力模型进行计算获得，其余参数通过测试得到，最后输出轧机轧制力。模型评价指标包括决定系数（R2）、平均绝对误差（MAE）与均方误差（MSE），评价指标结果，如表2所示。不同算法的拟合曲线，如图2～图4所示。

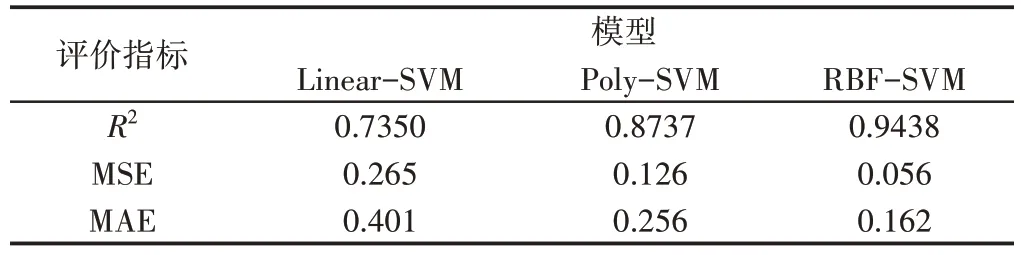
表2 评价指标结果Tab.2 Evaluation Index Results

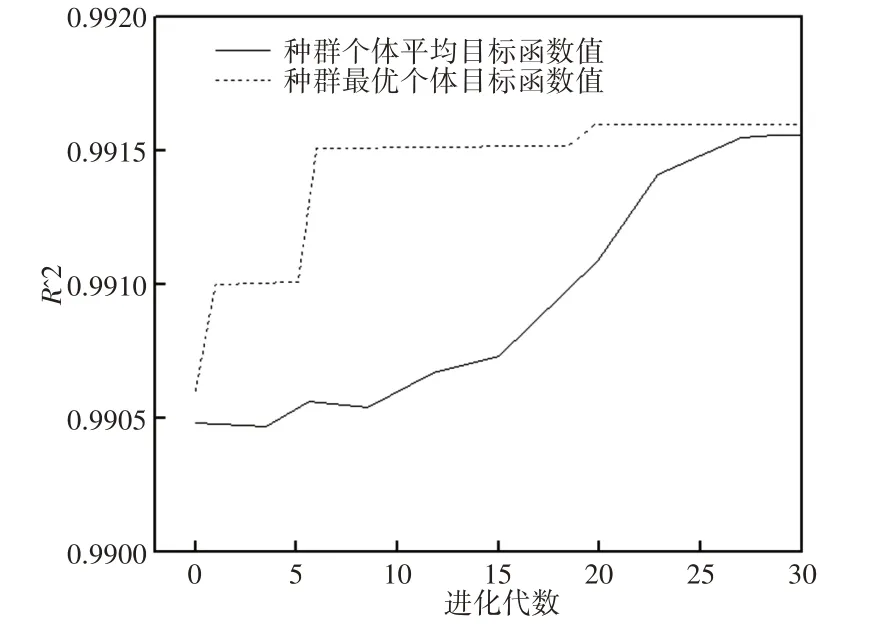
图2 DEI-RBF迭代曲线Fig.2 Iteration Curve of DEI-RBF

对表2分析发现，以RBF核函数构建的支持向量机回归模型获得了最大的R2，同时均方差（MSE）以及平均绝对误差（MAE）都达到了最小，显著提升了模型效果。

以RBF 作为核函数时得到了最优的模型拟合结果，其次为Poly核函数，效果最差的为Linear核函数。因此本实验将RBF核函数模型确定为基础模型。SVM回归模型处理性能受到惩罚系数C与核函数参数σ的直接作用，当C值越大时说明离群点受到更明显的重视，此时不会发生离群点丢失的情况。C值达到无穷大时，代表不能产生误差，从而较易发生过拟合的问题。σ属于一个固定系数，其值需满足大于0的条件。σ还会对训练集与测试集拟合性能也造成影响，当σ越大时，将会引起测试集拟合性能的变差，增加模型复杂度，引起泛化能力下降。利用差分进化算法对C与σ寻优够获得更高精度。

选择R2作为适应度函数，以随机方式生成一组初始［C，G］，总共进行30次初始化迭代，分别设定10、30、50、70的种群规模选择超参数结果，如表3所示。表3显示，在种群规模为50的情况下迭代30次后获得了最佳的模型效果。