一种防侧滑/侧翻的车辆路径规划方法
2023-09-21李伟文李亚峰
高 超,李 擎,李伟文,李亚峰
(北京信息科技大学高动态导航技术北京市重点实验室,北京 100192)
1 引言
汽车的使用很大程度上为人们的出行提供了便利,但是由于人的应急反应时间有限,对突现障碍物采取转向避障措施时往往发生交通事故。汽车安全早已成为社会关注的焦点问题[1]。为了降低交通事故发生率,无人驾驶技术的研究有着重要的理论意义和应用价值。避障路径规划算法作为无人驾驶的关键技术之一,也成为了研究的热点。常用的路径规划方法有基于节点的A*算法[2]和D*算法[3]、基于模型的人工势场法[4]、动态窗口法(Dynamic Window Approach,DWA)[5]等。文献[6]于2010 年提出了混合A*算法。该算法考虑了车辆的朝向以及运动学约束等条件,并在启发代价值的计算中加入了改变车辆运动方向的惩罚项[7],实现了非完整约束下的车辆路径规划。文献[8]将动态窗口法与阿克曼机器人相结合,提出了一个包含轨迹曲率相似度评价因子的局部路径规划算法,该算法能够在已知栅格地图内实现机器人的自主避障功能。文献[9]提出了限制小车加速度的范围对其速度空间约束进行优化,以避免出现过大的加速度导致轮胎垂直载荷过小造成运行不稳定的状况,然后又进行了轨迹误差补偿,解决路径偏离问题,该方法降低了路径平均误差。由于汽车行驶过程中,其轮胎垂直载荷的变化很难预测,直接以轮胎垂直载荷为指标来提高汽车运行稳定性的方法属于后验法,很难实现超前调整。文献[10]基于地图数据库和车辆定位设备研究了一种弯道车速控制系统,在此基础上,文献[11]设计了一种基于风险状态预估的弯道防侧滑超速预警系统。文献[12]使用S函数规划了初步避障路径,然后运用模型预测控制的方法进行了路径二次规划,以提高避障过程的安全性。文献[13]采用积分反推法设计了直道制动减速阶段的速度控制器,通过引入虚拟控制变量设计了弯道车道保持阶段的位姿控制器可以实现汽车驶入弯道前安全车速的控制,但是需要提前呈现出弯道信息,在车辆避障过程将无法使用。
为了提高车辆避障转向过程中横向稳定性,这里提出一种包含侧向加速度评价因子的动态窗口路径规划算法。由于车辆转向过程中前轮转向角有一定的范围,所以首先在动态窗口法中对速度和角速度空间的范围进行约束,使得规划出的路径能够满足车辆转向模型。然后在评价函数中加入侧向加速度评价因子对规划出的模拟路径的横向稳定性进行评价,最后根据总的评价函数得分选择最优路径。与原有的动态窗口法相比,该方法规划的路径更加平缓,横向稳定性更好,且能够一定程度上提高规划路径的效率。
2 车辆运动学模型
实际车辆的动力学特性十分复杂。为了便于研究车辆避障路径规划和横向稳定性,这里建立的车辆运动学模型保留侧向角速度、质心高度、转向速度等特性,忽略次要影响因素。建立的车辆运动学模型,如图1所示。
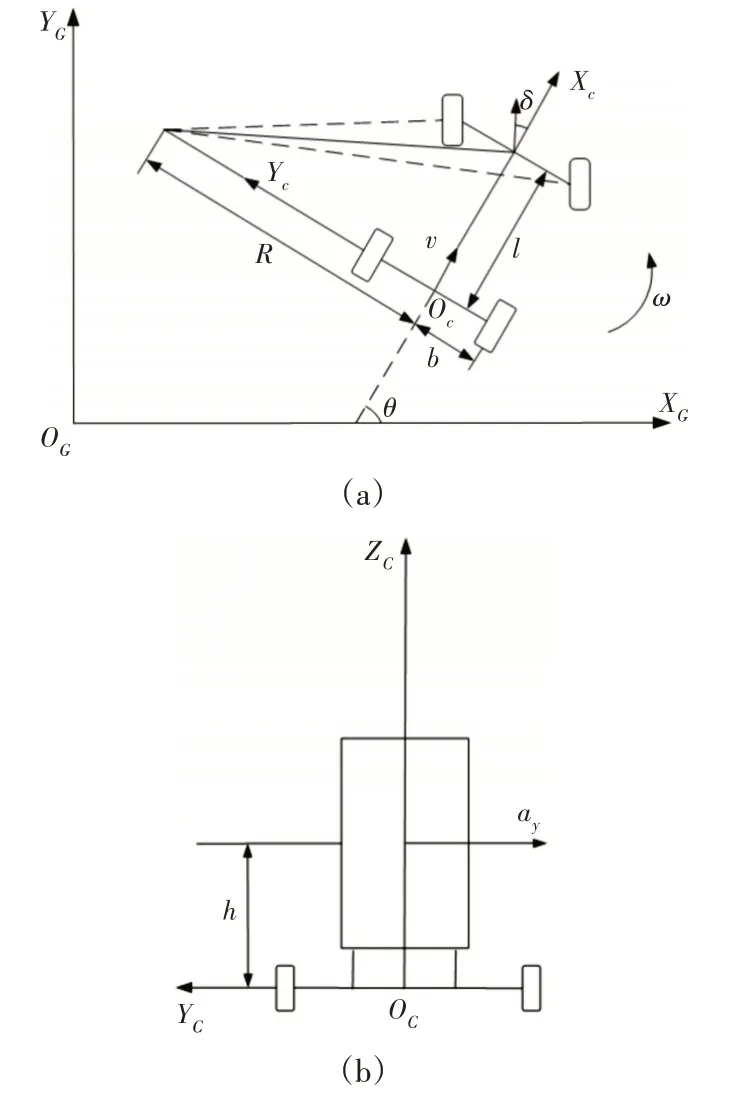
图1 车辆运动学模型Fig.1 Vehicle Kinematics Model
图中:δ—前轮转向角;R—转弯半径;v—车辆行驶速度;ω—转向速度;b—二分之一轮距;l—轴距;θ—全局坐标系(XGOGYG)与车体坐标系(XCOCYC)间的角度差;h—车辆质心高度;ay—侧向加速度。
根据图中几何关系可得:
由式(1)~式(3)可得:
为了便于研究车辆的运动轨迹以及运动过程中的横向稳定性,选择u=( )v,w作为控制输入量。则车辆运动学模型可表示为:
由上式可得,每Δt时刻内车辆的运行轨迹只取决于车速(v,ω),因此可以在车速构成的空间内进行运动规划,并且可以直接获取车辆在规划的路径运行时的侧向加速度,以分析车辆运行时的横向稳定性。
3 车辆横向稳定性分析
车辆避障转弯过程是一个曲线运动,该过程所产生的横向力应小于等于车辆所能提供的向心力,即离心力不超过轮胎与路面的横向附着力。由于车辆避障过程可能会出现车速高且转向幅度大,因而导致侧向加速度过大,致使横向附着力不足以克服离心力,车辆发生侧滑,同时由于质量在纵横方向上的转移,各轮胎上的垂直载荷会发生很大变化,车身向外倾斜,严重时会导致车辆侧翻。车辆行驶过程中的车速和旋转角速度直接关系到车辆避障转弯行驶时的安全性。
车辆避障转弯过程所行驶的道路有直道和弯道两种,两者的区别是有没有横向超高,为了方便分析车辆受力情况,设路面与水平面夹角为α,对转弯过程中的车辆进行受力分析可得:
式中:F—离心力;G—车重。其中α很小,可以认为sinα≈tanα=io,cosα≈1;io—路面横向超高的坡度,则车辆横向力为:
车辆不发生侧滑的条件离心力不大于轮胎与路面的横向附着力。即:
式中:φ—横向附着系数。由式(9)~式(10)可得车辆不发生侧滑的安全侧向加速度为:
车辆不发生侧翻的条件是侧倾力矩不大于稳定力矩。即:
式中:Fio≪G,可忽略不计,由式(9)、式(12)可得车辆不发生侧翻的安全侧向加速度为:
为保证车辆避障过程的横向稳定性,其侧向加速度需要同时满足上述两种约束条件,即:
综上分析可得,车辆避障转弯过程中,车辆参数b、h已知,所以安全侧向加速度与横向附着系数φ和路面横向超高坡度io有关,而车辆本身侧向加速度的大小取决于车速和转向角速度,因此,在侧向加速度到达临界安全值之前要对车速和转向角速度进行控制,避免车辆发生侧滑或侧翻事故。
4 改进动态窗口法
4.1 动态窗口法
动态窗口法是根据车辆运动学模型,在速度(v,ω)空间约束范围内,采集多组速度(vi,ωi),在设定的模拟时间内生成多条模拟轨迹,并根据轨迹评价函数对模拟轨迹进行评价,选出评价最高的轨迹作为车辆实际运动轨迹的方法。该方法是目前局部路径规划中比较主流的方法,能够实现实时避障。主要流程如下。
4.1.1 速度空间约束
(a)运动学约束Vs,即在车辆性能的限制下,能够达到的速度(v,ω)的上下限构成的空间。
(b)动力学约束Vd,即在加速度限制下,车辆当前线速度vc,当前角速度ωc,在dt时间内车辆能够到达的速度空间。
(c)障碍物约束Va,即车辆在轨迹末端不与障碍物发生碰撞的速度空间。
4.1.2 轨迹推算
在速度约束空间内进行采样,根据式(7)车辆运动学模型对采样的速度进行轨迹推算,可以得到多组模拟轨迹。
4.1.3 轨迹评价
在速度空间内生成的模拟轨迹理论上都是正确的,但是需要选择一条最优轨迹作为车辆实际运行轨迹,因此需要对轨迹进行评价。在路径规划中,我们希望车辆运行路径最优、时间最短且无碰撞,所以选择车辆的航向、速度、安全距离作为轨迹评价指标,根据实际情况为三个指标分配权重,最终求取总得分最高的轨迹既是最优轨迹。评价函数定义如下。
式中:heading(v,ω)—模拟轨迹终点车辆航向评分;dist(v,ω)—车辆与模拟轨道上最近障碍物间的距离,若无障碍物则设置为一个常数;velocity(v,ω)—模拟轨道对应的车辆行驶速度。
4.2 动态窗口法的改进
4.2.1 转向角约束
由于车辆是非完整约束的,不能原地旋转,所以在原有的速度空间基础上,根据转向角对旋转角速度加以限制,令Wδ表示转向角约束下的旋转角速度,则有:
因此,车辆速度空间约束为:
4.2.2 横向稳定性评价因子
横向稳定性的高低关系到车辆转弯、避障过程是否安全,判断横向稳定性的指标有很多,这里选择侧向加速度作为判定指标,其主要由转向角和车速决定。将侧向加速度作为横向稳定性评价因子对规划出的模拟路径进行评价,可以提前预测轨迹的横向稳定性,提高车辆行驶的安全性。新的评价函数如下:
式中:cros(v,ω)—侧向加速度评分,侧向加速度不小于安全侧向加速度时,评分设定为零,最大评分设置为大于零的常数,在此区间内,侧向加速度越小,评分越高。为式(21)中各项评价因子分配合适的权重,最终选择得分最高的速度对应的轨迹既是最优轨迹。
5 实验验证与结果分析
通常情况下,为了保证车辆安全,在车辆转向时,要求车辆侧向加速度不超过0.4g,该数据是在车辆行驶在附着系数良好的公路上,车辆处于线性工况下运动的要求[14-15]。为了验证这里提出的包含横向稳定性评价因子的动态窗口路径规划算法,设定侧向加速度阈值为0.3g,通过Matlab编程进行仿真研究。为分析横向稳定性评价因子对评价函数评估轨迹的影响,设计了四组实验进行验证,设定评价函数中前三个评价因子的权重α、β、γ不变,横向稳定性评价因子的权重分别设置为λ= 0、0.1、0.2、0.3四种情况,实验结果如下:
(1)λ= 0时,路径规划结果,如图2~图3所示。
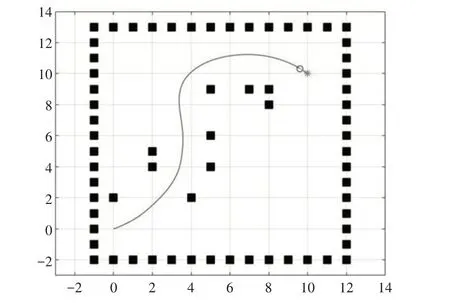
图2 λ = 0时路径规划结果Fig.2 λ = 0,Path Planning Results
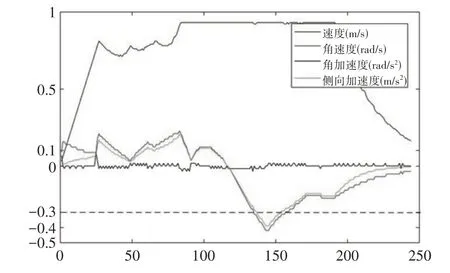
图3 λ = 0时参数曲线Fig.3 λ = 0,Parametric Curve
(2)λ= 0.1时,路径规划结果,如图4~图5所示。

图4 λ = 0.1时路径规划结果Fig.4 λ = 0.1,Path Planning Results
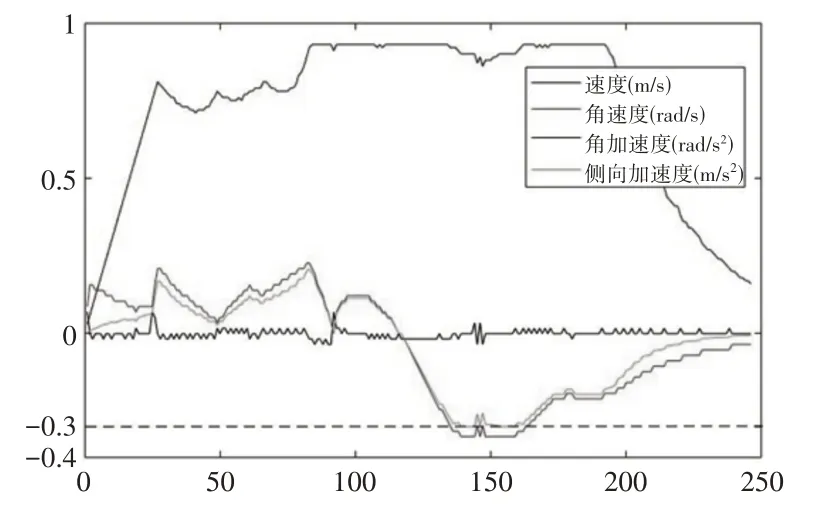
图5 λ = 0.1时参数曲线Fig.5 λ = 0.1,Parametric Curve
(3)λ= 0.2时,路径规划结果,如图6~图7所示。
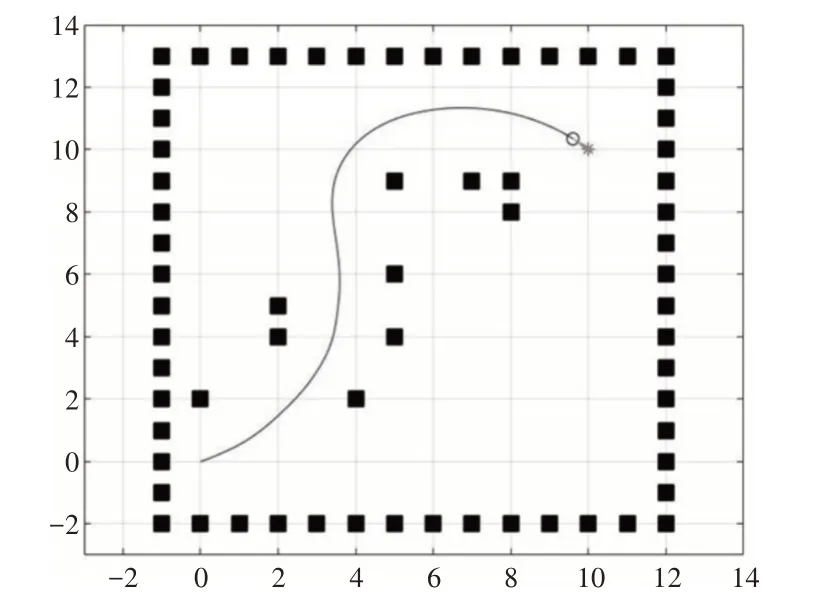
图6 λ = 0.2时路径规划结果Fig.6 λ = 0.2,Path Planning Results
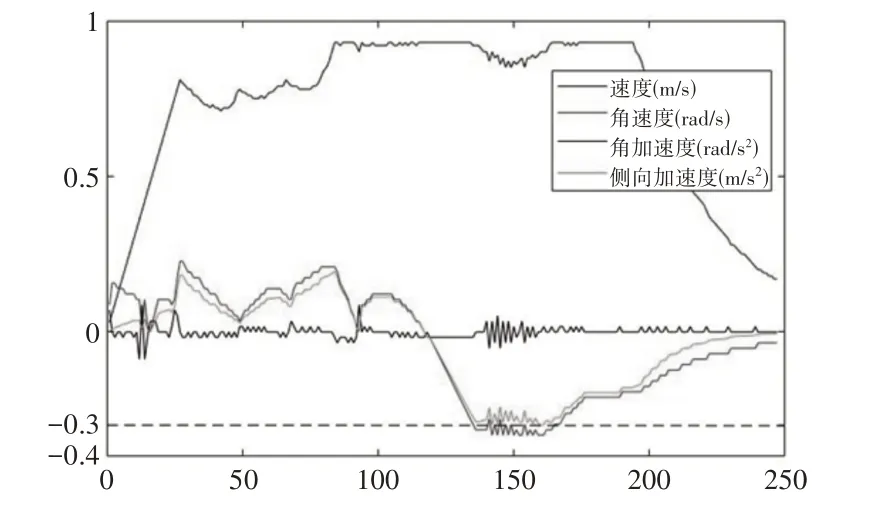
图7 λ = 0.2时参数曲线Fig.7 λ = 0.2 Parametric Curve
(4)λ= 0.3时,路径规划结果,如图8~图9所示。

图8 λ = 0.3时路径规划结果Fig.8 λ = 0.3,Path Planning Results
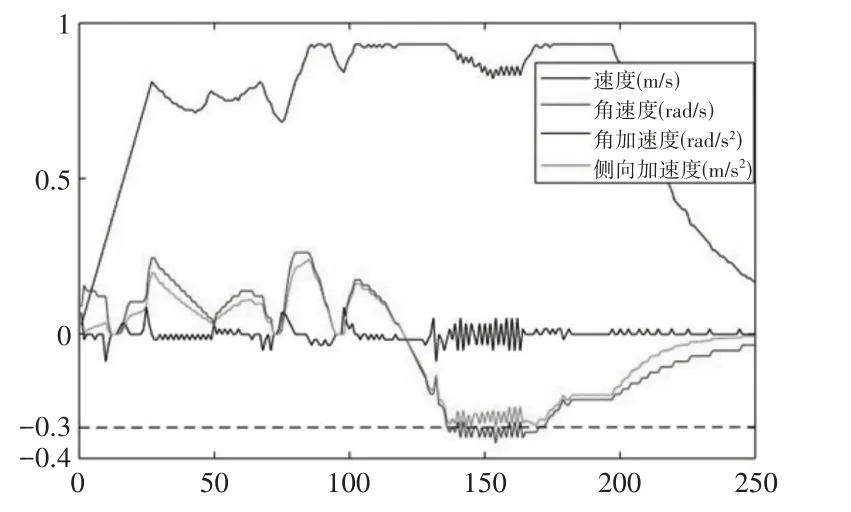
图9 λ = 0.3时参数曲线图Fig.9 λ = 0.3,Parametric Curve
四个不同权重下的实验结果对比,如表1所示。

表1 实验数据Tab.1 Experimental Data
由以上实验结果可以看出,在λ= 0时,规划的路径长度最短,且所花费的时间最短,但是最大侧向加速度绝对值最大且已超过设定的最大侧向加速度阈值。在为横向稳定性评价因子分配权重后,规划的路径长度和规划路径花费的时间都随着权重的增加而增加,虽然不同权重下最大侧向加速度绝对值相同,但是平均侧向加速度绝对值随着横向稳定性评价因子权重的增加有一定程度的降低。侧向加速度的大小反映了车辆行驶过程中横向稳定性的好坏,是关系到车辆能否安全避障、转弯而不发生侧滑/侧翻的重要指标,平均侧向加速大小的降低,说明规划的路径整体更加平缓。但是随着权重的增加,规划的路径长度和花费的时间在增加而平均侧向加速度大小在降低,因此,不同情况下可以为横向稳定性评价因子分配不同的权重,以规划出最合理的行车路径。
通过对实验结果分析可得,这里提出的包含横向稳定性评价因子的动态窗口路径规划方法可以实现对模拟路径的横向稳定性评价,选出可使车辆不发生侧滑/侧翻的路径。
6 结论
针对以往车辆路径规划中未考虑车辆横向稳定性的问题,提出了一种包含横向稳定性评价因子的动态窗口路径规划算法。该方法对车辆避障、转弯过程进行分析,根据车辆转弯过程中不发生侧滑/侧翻的条件(侧倾力矩不大于回正力矩)建立约束方程,以侧向加速度作为横向稳定性指标,并将其作为评价因子添加到路径选择的评价函数中,通过分配不同的权重进行对比实验,仿真实验结果表明,这里的方法可以有效影响规划路径过程中对拟选路径的选择,使得最终规划的路径更加平缓,路径对应的车辆侧向加速度更小,对路径规划中车辆横向稳定性方面的研究具有实际应用价值,在无人车避障转弯,汽车辅助驾驶等方面具有重要的应用价值。
