微细铣削表面形貌模型及工艺参数影响研究
2023-09-21唐先军唐方红
唐先军,唐方红,宋 跃
(1.东莞职业技术学院智能制造学院,广东 东莞 523808;2.东莞理工学院电子工程与智能化学院,广东 东莞 523808)
1 引言
随着先进制造技术的不断发展,微细铣削作为一种新型的加工制造方法,克服了传统MEMS技术的局限性,具有较高的加工效率以及良好的灵活特性,可以加工复杂的三维形状,具有广泛的应用前景[1-2]。
工件铣削后的表面形貌的形成取决于铣削运动中铣刀与工件之间的相对位置,受机床系统动态特性的影响。文献[3]利用有限元软件模拟分析了铝合金Al2024-T3在微细铣削下的热力耦合行为,在仿真结果的基础上分析了最优的工艺参数,仿真结果与现实结果具有较高的吻合性。文献[4]通过有限元法研究了铣削工艺参数对金刚石铣刀的铣削性能影响,通过实验验证了仿真分析的合理性。文献[5]研究了薄壁件的微细铣削,通过单因素试验分析了铣削工艺参数对薄壁件的表面质量加工的影响,研究表明走刀此次数能够减少其他因素对表面质量的影响。文献[6]研究了铣刀几何参数在微细铣削过程中对合金钢的加工表面质量的影响,通过正交实验分析了各种因素的最优组合。文献[7]利用金属切削软件模拟仿真了两种铝合金材料表面微细铣削行为特性,研究了不同铣削参数对表面形貌的影响。文献[8]通过齐次坐标矩阵变换建立球头铣刀形貌数学模型,利用Z-MAP方法提出了表面形貌算法,在此基础上对表面形貌进行了仿真分析,通过试验验证了所提模型和算法的有效性。文献[9]通过曲面薄壁件的微细铣削问题,开展了铣削参数对表面质量影响的试验研究,研究结果为提高加工质量和加工效率提供了理论依据。
目前虽然对微细铣削的三维建模做了一些努力,但没有充分考虑加工过程中动态响应和表面生成的影响,影响了这些表面形貌仿真的精度。基于此,本研究提出了一种考虑铣刀跳动、间歇切屑形成、最小切屑厚度和机床系统动态特性的微铣削表面形貌仿真模型,分析了微铣削表面粗糙度的影响因素。
2 微细铣削过程建模
本研究的铣削轨迹,如图1所示。为简化模型,假设进给方向为沿X轴方向。考虑到机床系统的动态特性,铣削的轨迹可表示为:
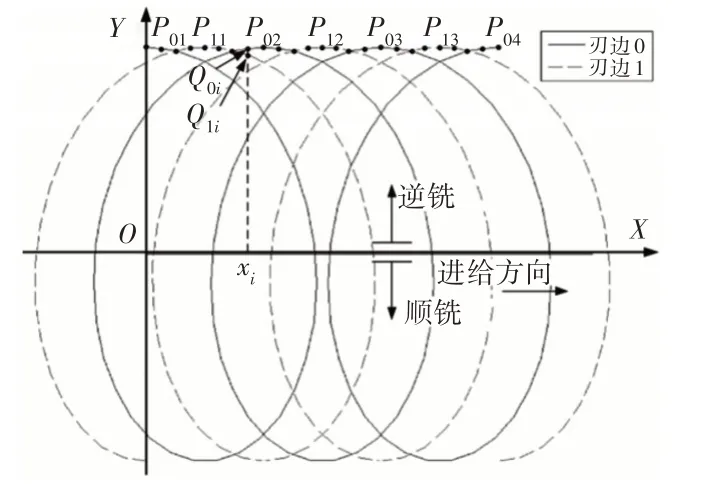
图1 铣刀轨迹图Fig.1 The Tool Trajectory Diagram
式中:f—进给速率;t—当前铣削力矩;R—铣刀半径;k—铣削刃的序号(k=0,1);K—铣削的刃数(K=2);ω—铣刀角速度;β—铣刀的螺旋角;r—铣刀跳动长度;θ—铣刀跳动角度;dx(t)、dy(t)、dz(t)—t时刻铣刀在X、Y、Z方向上的动态挠度。
由于铣刀轴向动刚度较大,Z向挠度可以忽略。机床系统在X方向和Y方向上的动力学特性是相同的,dx(t)和dy(t)可由下式可得:
式中:Fx、Fy—X方向和Y方向的切削力,由微铣削力模型进行预测[10];Gd—铣刀的脉冲响应函数,通过响应耦合法获得[11]。
(1)当瞬时待切屑厚度ha(t,k,z)小于最小屑厚,则:
(2)当瞬时待切屑厚度ha(t,k,z)大于或等于最小屑厚,则:
式中:At、Bt—切向力系数;Ar、Br—径向力系数;Aa、Ba—轴向力系数;Ats、Btp—切向剪切力和犁削力系数;Ars、Brp—径向剪切力和犁削力系数;Aas、Bap—轴向剪切力系数和犁削力系数。这里选择最小切削厚度为0.8μm[12]。通过方程(5)将dFt,dFr和dFa转换到Oxyz坐标系:
以铣削中的双刃铣刀为例,如图1所示。首先计算极值点P0m和P1m(m=1,2,…),且逆铣满足式(6)条件,顺铣满足式(7)条件:
由上式可知,在tkm时刻的极值点满足下列方程:
采用迭代算法求解这些非线性方程组,考虑到铣削轨迹的周期性,初始值的选择如下:
将tkm代入式(1),得到极值点坐标。假设ti是铣削边k在xi处的时间,为计算yi对应的值xi,将式(1)在xi最近的极值点内用一阶泰勒级数展开,并保留一次项,然后可以得到以下方程式:
将ti代入式(1)中,可以计算靠近极值点的点(Q0i,Q1i等)的坐标,逆铣和顺铣分别对应最大值和最小值。任意点的铣削表面误差可由下式求得:
通过表面粗糙度Ra评价铣削表面质量和精度,可以由表面误差的算术平均偏差来计算,如式(12)所示。
3 实验模型
相对于传统的铣削加工,微细铣削加工中的影响因素更为复杂。本研究选择主轴转速、进给速度、径向切深和铣削模式作为主要因素,分别并将其编码对应为A、B、C和D,如表1所示。铣削的轴向深度和铣刀直径分别为100μm 和1mm,铣刀跳动长度和角度分别为5μm和110°。

表1 正交实验参数设置Tab.1 Parameter Setting of Orthogonal Experiment
本研究利用五轴微细铣削机床和铝合金进行了实验,如图2所示。分别采用表1所示的正交试验参数进行铣削试验,通过基恩士(KEYENCE)形貌显微镜对铣削后的工件表面进行表面形貌的测量。并在同样试验参数条件下,根据所提的模型对表面粗糙度进行预测,对比了表面粗糙度的预测值和试验的测量值,可以看出预测结果与实测值的吻合性较好,如图3所示。而在微细铣削加工过程中,由于影响表面形貌的加工因素更加复杂,通常预测值要小于测量值。

图2 微细铣削实验平台Fig.2 Micro Milling Experimental Platform

图3 表面粗糙度的预测和测量Fig.3 Prediction and Measurement of Surface Roughness
4 仿真结果的分析
4.1 表面形貌的影响分析
选择A1B2C2D1 组合的铣削参数(主轴转速为30000r/min;进给速度为0.65mm/s;径向切深为170μm;逆铣)为例,对微细铣削的表面形貌进行模拟,模拟结果,如图4(a)、图4(b)所示。图4(a)描述了不考虑铣刀跳动和动挠度的情况,表面形貌取决于铣削刃、主轴旋转和进给运动的综合作用。而当考虑铣刀跳动的情况时,铣刀的跳动长度和角度则是决定表面形貌的主要因素,如图4(b)所示。同样,图4(c)所示为考虑到铣刀的动态变形情况下的表面形貌情况,与图4(b)相比,可以看出铣刀跳动和动态变形的叠加导致表面误差的幅值增大。

图4 表面形貌的模拟结果Fig.4 Simulation Results of Surface Morphology
使用基恩士(KEYENCE)对铣削后的表面形貌进行测量,测量面积为(50×50)μm,分辨率为0.7μm,结果,如图5所示。从图中可以看出,表面形貌的点大部分集中在某一区域范围,由于毛刺等加工因素造成某些区域的超出该区域范围。可以看出所提出的表面形貌算法能够准确地模拟微细铣削的表面形貌。

图5 表面形貌的测量Fig.5 Measurement of Surface Morphology
其他仿真结果,如图6所示。从图中可以看出,各影响因素分析如下:

图6 表面形貌模拟结果(A3B2C2D1)Fig.6 Surface Morphology Simulation Results(A3B2C2D1)
(1)主轴转速:当主轴转速为50000r/min,其他参数保持不变(A3B2C2D1)时,仿真表面形貌,如图6所示。对比图6和图4(c)可以看出,表面形貌变得更加崎岖,表面误差值增大,主要原因可能是这些铣削参数的主轴转速频率更接近机床系统固有频率,导致铣刀的偏转变大。此外,铣削的每齿进给量都比较小,导致频繁的犁削以及较大的铣削力,也会导致较大的铣刀挠度。
(2)进给速率:当进给量选择0.9mm/s,其他参数(A1B3C2D 1)不变时,模拟的表面形貌,如图7所示。对比图7和图4(c)可以看出,表面误差值有所增加,主要原因是每齿进给量随着进给速度的增加而增加,导致了犁削的减少,但随着剪切力的增大,铣刀挠度增大。

图7 表面形貌模拟结果(A1B3C2D1)Fig.7 Surface Morphology Simulation Results(A1B3C2D1)
(3)径向切削深度:当径向切深选择250μm 时,其他参数(A1B2C3D1)不变时,模拟的表面形貌,如图8所示。对比图8和图4(c)可以看出,表面形貌变得更加崎岖,表面误差值增大,这主要原因是随着径向切深的增大,铣削过程中的铣削力增大,导致铣刀的挠度增大。
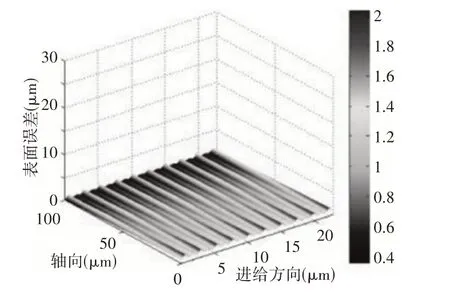
图8 表面形貌模拟结果(A1B2C3D1)Fig.8 Surface Morphology Simulation Results(A1B2C3D1)
(4)铣削模式:当选择顺铣时,其他参数不变(A1B2C2D2)时,模拟的表面形貌,如图9所示。对比图9和图4(c),可以看出铣削的表面形貌和误差没有明显变化。

图9 表面形貌模拟结果(A1B2C2D1)Fig.9 Surface Morphology Simulation Results(A1B2C2D1)
(5)铣刀直径:当使用直径为1mm的铣刀,且其他铣削参数不变时,模拟的表面形貌,如图10所示。对比图10与图4(c),可以看出表面形貌变得更加光滑,表面误差值减小,这主要是由于机床系统的动刚度随着铣刀直径的增大而增大,使得铣刀挠度减小。
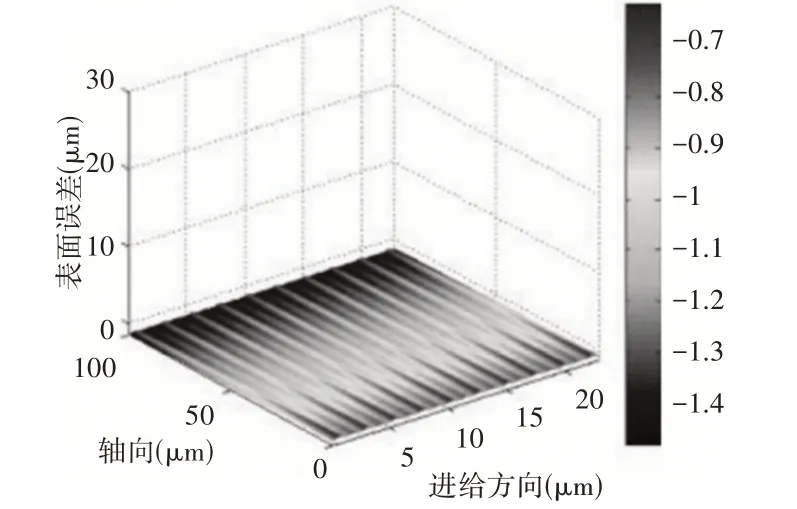
图10 表面形貌模拟结果(铣刀直径为1mm)Fig.10 Surface Morphology Simulation Results(Milling Cutter Diameter is 1mm)
(6)铣刀跳动:铣刀跳动对表面形貌的影响最为显著,尤其是轴向切削深度较大(400μm)时。模拟的表面形貌,如图11~图13所示。可以看出铣刀跳动对表面形貌起着决定性的作用。当铣刀跳动角(0°)变化时,对比图12与图4(c),可以看出表面误差值明显减小,这是因为当铣刀无跳动角时,其对刀尖铣削过程中的轨迹影响最大,抵消了铣刀挠度对表面误差的影响。当铣刀跳动长度改变(1μm)时,如图13所示。与图4(c)相比,铣刀跳动对铣刀挠度的偏移影响减小,导致表面误差值增大。

图11 表面形貌模拟结果(轴向切深为400μm)Fig.11 Surface Morphology Simulation Results(Axial Cutting Depth is 400μm)

图12 表面形貌模拟结果(铣刀跳动角度为0°)Fig.12 Surface Morphology Simulation Results(Milling Cutter Runout Angle is 0°)

图13 表面形貌模拟结果(铣刀跳动长度为1μm)Fig.13 Surface Morphology Simulation Results(Runout Length of Milling Cutter is 1μm)
4.2 表面粗糙度的影响分析
在微铣削加工中,表面粗糙度很难控制,因此如何降低表面粗糙度成为研究热点。本研究采用方差分析(ANOVA)对测量的表面粗糙度进行影响因素分析结果,如表2所示。

表2 方差分析结果Tab.2 Analysis of Variance Results
从方差分析结果表明主轴转速(A)是微细铣加工中最显著的影响因素,进给量(B)和铣削方式(D)也有很大的影响。但径向切深(C)对表面粗糙度的影响不显著。此外,主轴转速与进给速率(AB)之间的交互作用也有显著影响。方差分析结果与所提出的表面形貌模型相似,说明所建立的仿真模型能在一定程度上准确地反映铣削后的表面形貌,并能很好地解释表面粗糙度的影响因素。
5 结论
提出了一种微细铣削加工的表面形貌模型,并通过仿真模型和方差分析对影响表面形貌的因素进行了分析。分析结果表明微细铣削的表面形貌与常规铣削有较大的不同,具有以下特点:(1)主轴转速是影响微细铣削表面形貌最显著的因素。当主轴转速频率接近机床系统固有频率时,铣刀的偏转显著增加,导致表面误差增大。(2)在微细铣削加工中,表面误差并不是随进给速度单调增加的,当进给速度较低时,连续犁削导致工件与铣刀刃间的摩擦迅速增加,单位切削力也增加,这导致表面误差增大。此外,前刀面与切屑之间的摩擦增大,使铣刀容易粘附而增大表面粗糙度。随着进给速度的增加,犁耕减少,从而减少了表面误差。(3)表面误差不随径向切深单调变化,切削力随径向切深的增大而增大,从而增大表面误差。另一方面,如果铣削径向切深过小,较小的瞬时待切削切屑厚度反而增大了犁削量,也会增加表面误差。
