采煤机截割部传动系统机电耦合动力学仿真分析

石鑫彬，王义亮

（1.太原理工大学机械与运载工程学院，山西 太原 030024；2.煤矿综采装备山西省重点实验室，山西 太原 030024）

1 引言

采煤机截割部对煤炭开采效率有着极其重要的影响。采煤机截割部主要由滚筒、摇臂壳体和齿轮传动系统等机构组成。目前，诸多学者对于截割部传动系统进行了动力学研究分析：文献［1］从接触理论的角度结合采煤机截割部仿真分析项目，探讨描述了齿轮动态啮合过程和齿轮传动动力学模型方法；文献［2］研究了不同牵引速度下采煤机传动系统高速级齿轮啮合力的变化，发现二者之间存在极强的线性关系；文献［3］模拟滚筒实际截割煤层时受到的载荷，对截割部摇臂齿轮系统进行平移-扭转动力学仿真分析；文献［4］研究了电动机-齿轮传动系统的连接阻尼和刚度对截割部机电传动系统动力学特性的影响；文献［5］建立了截割部齿轮传动系统的非线性动力学模型，应用变步长龙格-库塔方法求解系统微分方程，研究了啮合刚度、阻尼比及激振频率对传动系统动态特性的影响。

上述研究中输入转速多采用定值，电机输出转速不随负载波动而变化，因而仿真中无法反映电机的动态特性。针对此问题，建立了一个包含动态电动机的截割部传动系统机电耦合动力学模型，研究了空载启动时和受到冲击载荷时，电动机的输出转速响应及截割部传动系统的动力学响应。

2 截割部机电耦合模型建立

2.1 采煤机截割部三维模型建立

某型号采煤机截割部传动系统包括两级行星齿轮传动和两级平行轴传动。根据齿轮参数在三维建模软件UG中建立齿轮传动系统模型，并与壳体进行装配。齿轮参数，如表1所示。在UG中转化为Parasolid格式文件后导入Adams中，如图1所示。

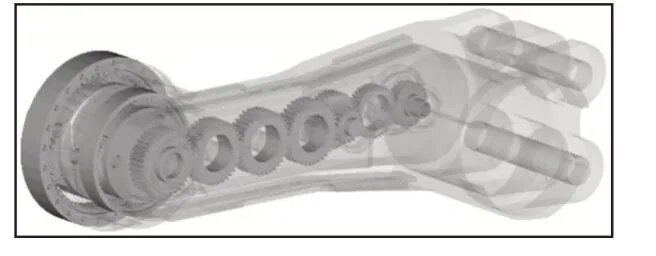
图1 采煤机截割部模型Fig.1 Model of Shearer Cutting Part

表1 传动齿轮参数Tab.1 Parameters of Transmission Gears

2.2 约束及接触的添加

模型导入后还需要添加部件之间的约束，以及齿轮间的接触力。运动副，如表2所示。

表2 运动副设置Tab.2 Constraints Between Components

Adams中的接触算法包括基于补偿的接触算法和基于碰撞函数的接触算法，这里采用碰撞函数研究齿轮的传动。计算公式为：

式中：K—刚度系数；q0—两物体未发生穿透时的最小距离；q—两物体实际距离；e—碰撞指数；d0—穿透深度；c—阻尼系数。

刚度系数K按照赫兹接触公式［6］计算：

其中：

式中：R1、R2—两物体的曲率半径；E1、E2—两构件的弹性模量；u1、u2—两构件的泊松比，计算后的各齿轮间接触刚度设置，如表3所示。

表3 接触刚度设置Tab.3 Contact Stiffness Setting

阻尼系数c选取5.0e+04N·s-1/m，力指数e取1.5，穿透深度选1.0e-04m。静摩擦系数选取0.08，动摩擦系数选取0.05，静滑移速度取1.0e-04m/s，动滑移速度取1.0e-03m/s。

2.3 采煤机截割部电动机建模

采煤机截割部所用电动机为三相异步交流电动机，异步电机的数学模型是一种高阶、非线性、强耦合的多变量系统，在研究异步电机的模型时，常作如下假设：（1）忽略空间谐波，设三相绕组对称，产生的磁动势按正弦规律分布在气隙圆周；（2）忽略磁路的饱和，各绕组的电感和互感恒定；（3）忽略铁芯的损耗；（4）绕组电阻恒定，不随频率和温度变化。

Simulink的异步电机数学模型在任意二相旋转坐标系下的电压方程如下：

磁链方程为：

式中：Rs、LIs—定子电阻和电感；R'r1、L'Ir1、R'r2、L'Ir2—双笼的转子电阻和电感；Lm—定转子互感；p—极对数；ω—定子相对于参考系的角速度；ωm—转子角速度；ωr—电角速度，ωr=ωm×p；H—惯性时间常数；Te—电磁转矩；Tm—负载转矩。

利用Simulink所建立电动机模型的输入为负载转矩，输出为转子转速、定转子电流等，如图2所示。电动机主要参数，如表4所示。

图2 截割部电动机模型Fig.2 Motor Model of Cutting Part

表4 电动机参数Tab.4 Parameters of Motor

2.4 采煤机截割部机电耦合模型建立

采煤机运转时，截割电动机的负载转矩为截割部传动系统截一轴的转矩，同时，截割电动机输出转速通过扭矩轴传递给截一轴，为传动系统提供动力。为了实现该过程的仿真，需要在Adams模型中添加两个状态变量，分别用来输出截一轴转矩和获取电动机转速。将传动系统模型的控制方程导出，在Simulink中与电动机模型组合成机电耦合动力学模型，如图3所示。

图3 机电耦合动力学模型Fig.3 Electromechanical Coupling Dynamic Model

3 机电耦合动力学仿真

3.1 载荷设置

系统的转速由电动机输出，额定负载T=3.6×105N·m，冲击动载荷峰值设定为2倍的额定负载T1=7.2×105N·m。冲击动载荷利用STEP函数施加在二级行星架的输出端，在（3.0～3.25）s内迅速增加至T1，在（3.25～3.5）s内减少到0。载荷图像，如图4所示。为了获得平稳输出，设定仿真时间为5s，仿真步数设定为10000步。

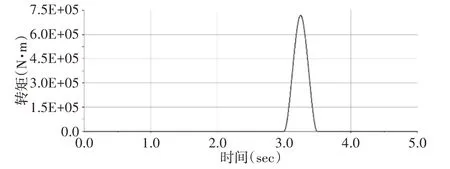
图4 动载荷曲线Fig.4 Impact Load Curve

3.2 仿真分析

仿真结束后，通过示波器观察电动机的负载及输出角速度图，如图5所示。可以看出：在空载启动时，采煤机电动机在0.5s内由0deg/s提升到9000deg/s，期间电动机转速多次波动，最多达到9250deg/s。在（0.5～3）s 时间段内稳定在9000deg/s，此时速度有轻微波动，是因为传动系统中齿轮接触会产生冲击，但总体角速度保持稳定，等于电动机的同步转速1500r/min。在（3.0～3.25）s加载冲击动载荷时，电动机受到的负载转矩提升至2480N·m，电动机输出的角速度降低至8971deg/s，在（3.25～3.5）s，冲击动载荷减小的同时，电动机转速也逐步提升至9000deg/s并平稳保持至仿真结束。电动机的转子转速随着负载转矩的提升而降低，随着负载转矩的降低而升高，说明该模型中的电机模型为动态的，能够根据负载实时反映速度变化。

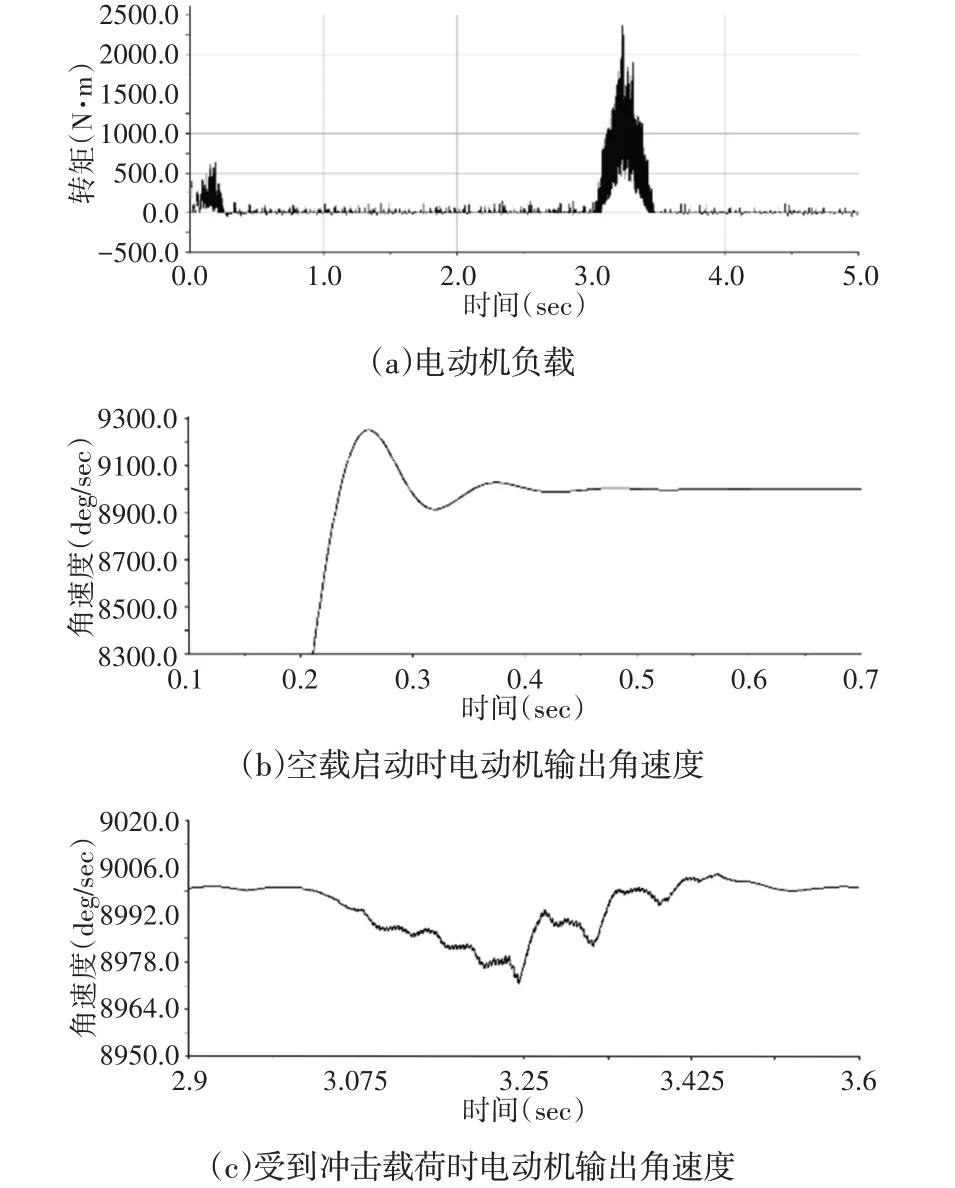
图5 电动机负载及输出角速度Fig.5 Motor Load and Output Angular Speed

提取各传动轴的角速度，如图6所示。并计算空载时各轴角速度的均方根值（RMS）并与理论值对比，如表5所示。可以看出各轴的角速度与理论值误差极小，符合该采煤机传动比。随着传动轴与电动机输出端的距离增加，误差逐渐增大，是因为动力从电动机传递到输出端，各齿轮接触时产生的传动误差累计。但最大偏差也不高于1‰，证明了该动力学模型的准确性。

图6 截割部传动系统各传动轴角速度Fig.6 Angular Velocity of Each Drive Shaft

表5 稳定时各传动轴角速度及误差Tab.5 Angular Velocity and Error of Each Drive Shaft when Stable

以一、二级行星架为例，研究加速度及其频域曲线。通过Adams后处理提取传动系统一、二级行星架的加速度时域图，并进行快速傅里叶变换（FFT），导出频域图，如图7所示。根据公式f行星=n·z（n为行星架转频，z为内齿圈齿数），计算出一、二级行星齿轮传动的啮合频率分别为142.74Hz和26.76Hz。观察图7发现一级行星架加速度在147.21Hz 及其倍频287.84Hz 和428.34Hz处幅值较大，二级行星架加速度其26.73Hz及其倍频53.47Hz和80.31Hz等频率处幅值较大。仿真所得结果符合计算得出的啮合频率。一、二级行星架的加速度仿真全程均处于波动状态，但在施加突变动载荷时，加速度振动幅度大幅增加，一级行星架的加速度幅值达到36028deg/s2，二级行星架的加速度幅值达到12266deg/s2，冲击载荷会使行星架承受极大冲击。

图7 冲击动载荷下，一、二级行星架加速度及其频域曲线Fig.7 Under Impact Load，the Acceleration of Primary and Secondary Planet Carrier and its Frequency Domain Curve

4 结论

（1）利用Adams和Simulink软件，建立了一个包含电动机的截割部机电耦合动力学模型，仿真得到空载启动和冲击载荷条件下，截割部电动机的输入输出曲线、传动系统各齿轮的角速度和加速度响应。角速度响应和加速度啮合频率符合计算结果，验证了动力学模型的准确性。（2）机电耦合模型能够对负载做出实时反馈，当对二级行星架施加二倍负载大小的突变动载荷时，电动机输出转速降低至8971deg/s，各齿轮的角速度波动幅度大幅增加，一、二级行星架的加速度振动幅值达到空载两倍以上。说明该机电耦合模型与以往的固定输入转速的动力学模型相比，能够根据负载的添加动态改变转速输入，更加准确地对截割部传动系统进行动力学仿真，对采煤机截割部的后续分析和优化提供了依据。