平滑支持向量模型预测控制集气管压力

2023-09-21李志刚孙益亮

机械设计与制造 2023年9期

李志刚，孙益亮

（1.华北理工大学人工智能学院，河北唐山 063210；2.华北理工大学电气工程学院，河北唐山 063210）

1 引言

在工业上，焦炭并不会直接将原煤进行焚烧使用，而是先将原煤进行工艺加工，当原煤进行焦化的时候，需要将煤炭在高温隔绝空气的环境下在炭化室干馏最终成为焦炭，而在焦炉的炭化室内，会伴随产生一种可燃烧的气体—荒煤气。因荒煤气尚未经过净化处理，其中包含硫、一氧化碳、氰化物等有害气体，为了保护环境，需将荒煤气进行回收，集气管属于荒煤气回收的重要设备。

集气管压力是焦炉生产中重要的工艺参数，在焦化生产过程中，集气管压力的变化因受多种因素的影响［1-2］，例如：出焦、装煤及管道阻力等的影响而常常发生波动。为了保证生产安全，提升产品质量以及保护环境和延长锅炉的使用寿命，需要对集气管压力进行控制，使其能够稳定在生产工艺所需的范围内［3-4］。

随着计算机技术的发展，集气管压力控制控制开始了计算机控制的阶段，如很多的工厂使用了单片机、PLC 等系统，可以更加简便的对集气管压力进行自动调节控制［5］，但由于集气管压力系统是一个非线性、强耦合的时变系统，这些微机控制很难做到快速响应的要求［6］。近些年，神经网络与模糊控制开始在工业生产上使用，人们开始将模糊控制应用到实际，取得了良好的控制效果［7］。

而随着数据挖掘技术的发展与成熟，工业生产设备的控制方法开始使用智能控制方法［8］，利用前期的采集到的数据，从数据中挖掘出隐藏的规律，实现工业生产的预测性控制，大大提高了生产效率以及生产的安全性。这里在支持向量机控制的基础上，提出了一种平滑的支持向量模型，将采集到的数据先进行平滑性处理，在利用支持向量机模型进行数据的预测控制，提高非线性逼近功能。

2 数据处理

以唐山某炼焦制气厂为例，利用炼焦制气时每秒采集的集气管压力值而形成的数据集，利用这些数据可以从中挖掘出数据之间的隐藏规律，将这些隐藏规律。为了消除噪声数据对实验的干扰以及对数据的，需要先将采集到的数据进行处理。

2.1 异常数据处理

在使用的数据中，由于数据的来源为工程实际，采集到的数据受到的现场环境变化的影响，往往会夹杂着许多的噪声高的现象，为了降低噪声数据对实验的影响，需要将噪声数据找出并剔除出去，例如数据：

66666.00 02 -Feb-06 08：04：54.62500、Bad 05-Feb-06 12：50：26.85800，这些数据明显偏离正常值或者采集出现错误，通过数据集成、清洗、变换、简化的方法将噪声数据处理并补充完善数据集。

2.2 数据平滑

相对于支持向量模型，平滑支持向量模型的不同之处在于一个内置的特殊的滤波器，用于数据的平滑处理，从而使集气管的数据的异常值和噪声的对实验的影响降低到最小，其模型结构，如图1 所示。此模型由三个功能部分组成：数据采集，平滑和非线性逼近。

图1 平滑支持向量机模型结构Fig.1 Smooth Support Vector Machine Model Structure

平滑方法使用基于最小二乘的卷积拟合算法，它是在卷积过程中计算得到，利用线性最小二乘法产生低阶多项式拟合相邻的数据点，其表达式为：

式中：x—输入数据；Ci—卷积系数；m—卷积的次数。

2.3 数据训练集与测试集

利用前期从炼焦制气厂采集到的数据，对模型进行训练，利用数据中前3/4的数据作为训练集，通过数据预处理，在进行数据训练，实现对后四分之一的数据的预测输出，而后四分之一作为测试集，可以比较出预测值与真实值之间的误差，通过均方根误差的大小比较出模型的可行性。

3 LS-SVM理论介绍

目前，许多机器学习方法被用于集气管压力控制，其中，SVM因其在处理小数据方面的突出表现，被广泛的应用，但是由于数据的复杂性，仍存在很多的不精确的地方［9］，现提出一种平滑的LS-SVM的方法，可以有效提高非线性的逼近性能［10］。其回归模型，如式（2）所示。

式中：ω—权重向量；φ(x)—一个可以实现高维映射的非线性函数；b—偏置。

这里为增强x和y的适应构建了一个分割超平面。

在结构风险最小化条件下，可建立优化目标，将复杂的最小二乘支持向量机回归问题转换为优化问题，目标函数为：

约束条件为：

式中：ei—误差向量；C＞0—正则化参数。

采用拉格朗日乘子法，上述问题可以被如下的拉格朗日函数解决：

式中：αi—拉格朗日乘子。

上述式（5）可以对每个变量求偏微分进行求解：

消掉变量ω和e，可以得到线性方程：

其中，

且有Ωij=φ(xi)φ(xj)=K(xi，xj)，i，j=1，2，3，…，l，其中，K(xi，xj)是一种核函数，并且满足Karush-Kuhn-Tucker条件。在训练工作中，选择了多项式函数，公式如下：

基于式（7），α和b被计算出，平滑优先LS-SVM 模型则训练完毕：

4 仿真结果及分析

本节将进行算法模型的搭建，将公式转换为程序语言，利用MATLAB编程软件，实现算法模型的搭建与实验的完成。

为了验证算法模型的可行性与效果，需要进行BP模型以及LS-SVM 模型的搭建，通过对相同的数据集进行训练，观察对比相同预测值的情况下，预测值相对于实际值的抖动情况以及均方根误差大小，判断模型的预测效果。

在实验条件相同的情况下，通过对比预测结果的均方根误差以及误差抖动的剧烈程度，可以对比出模型的优劣处，各个模型的输出结果，如图2～图4所示。

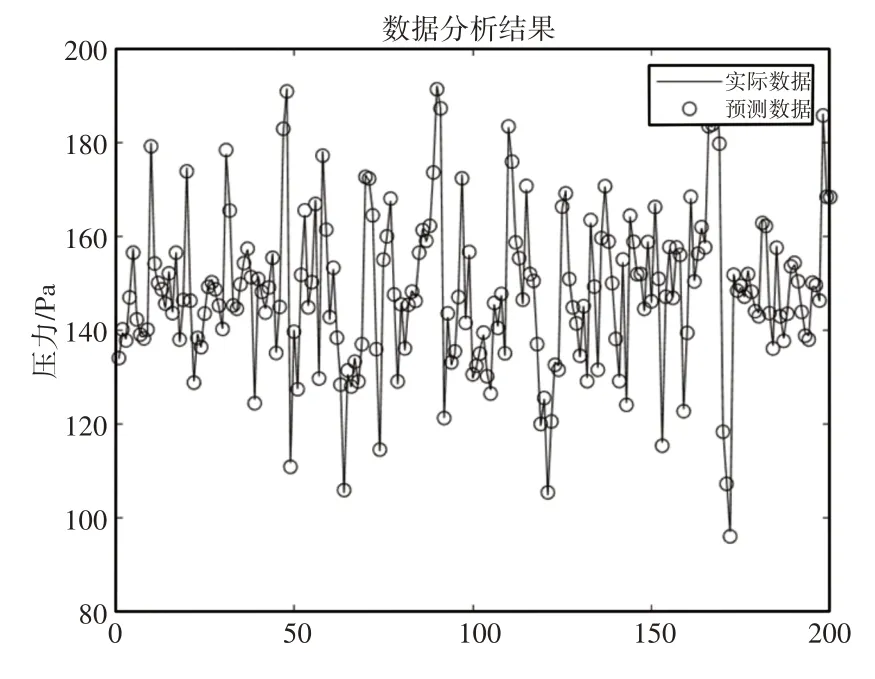
图2 平滑支持向量模型预测结果Fig.2 Smooth Support Vector Model Prediction Results

图3 LS-SVM网络模型预测结果Fig.3 LS-SVM Network Model Prediction Results

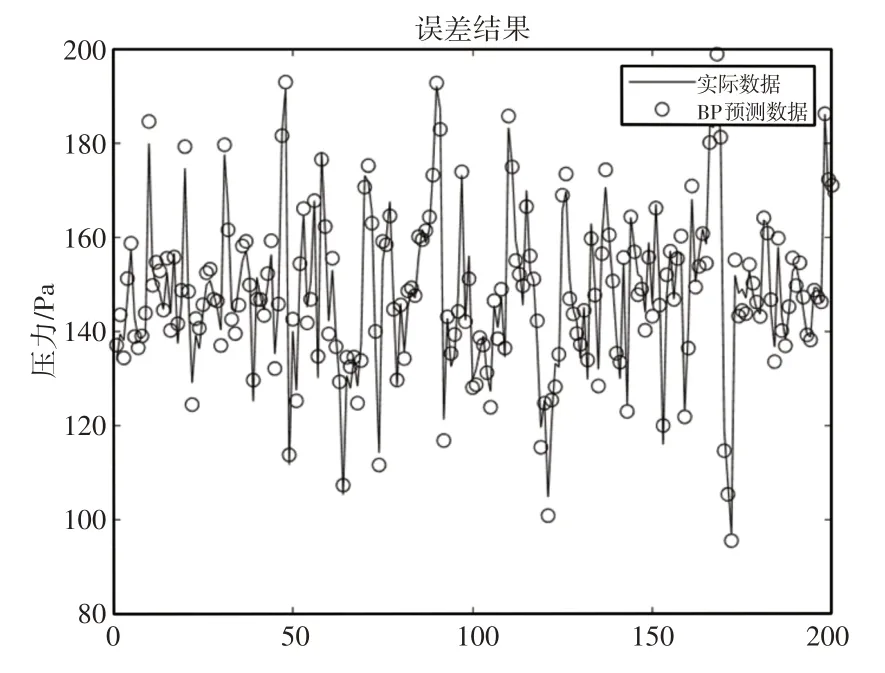
图4 BP网络模型预测结果Fig.4 BP Network Model Prediction Results

通过图2～图4中各模型的预测结果与实际结果的对比，可以直观的看到BP网络模型的预测结果在集气管压力波动较大的拐点处有较大的误差，预测效果不理想，而平滑支持向量模型与LS-SVM模型的预测结果与实际结果相差较小，无法直观的看出优缺点，为了进一步比较模型的效果，通过比较均方根误差的大小进行判断，各模型的均方根误差值，如表1所示。