超声阵列方法在层状结构损伤检测中的应用*

张邦

(中铁第四勘察设计院集团有限公司 武汉 430063)

0 引言

层状钢筋混凝土是工程建筑中常见的一种结构，各层结构内部损伤以及层间离缝脱空直接影响到整体结构性能。高铁无砟轨道是一种典型的层状结构，主要由上层的轨道板、下层的支承层以及层间的砂浆层构成。无砟轨道直接承载着高速列车通行，其质量好坏、病害与否直接关系到列车运营安全。作为一种露天放置、反复承受列车荷载的层状结构，无砟轨道在长期服役过程中，在列车荷载、温度变化、基础变形以及混凝土自身收缩变形的影响下容易产生裂缝、离缝、脱空等缺陷。

目前我国运营高铁里程超过4×104km。国内针对高铁无砟轨道无损检测的研究较多，常见物探方法主要有：地质雷达法、冲击回波法等。地质雷达探测方法以其高效、无损的特点被广泛用于高铁轨道缺陷探测。廖建红等[1]通过数值模拟的方法给出了砂浆层缺陷的雷达图像特征；张邦[2]使用地质雷达探测沪杭高铁无砟轨道沉降及并结合注浆前后雷达资料评价治理效果，然而使用地质雷达方法受到高铁无砟轨道混凝土结构内部钢筋网的干扰屏蔽作用，导致缺陷检测的精细程度不高。冲击弹性波响应方法主要用于查明轨道板以及支承层间病害，汤政[3]、武思思[4]、钟鹏飞等[5]对高铁无砟轨道线下不同层间病害建立物理实验模型进行理论分析，通过弹性波动力学响应及时频特性判断轨道缺陷，该类方法根据缺陷部位对弹性波的振动响应差异来判识轨道线下结构病害，只能做到定性判识缺陷位置，无法定量评估缺陷的深度及大小。

超声波方法用于混凝土结构的检测较多。严武平等[6]对使用单点超声波法检测高铁轨道板层间缺陷，利用频谱特征定性地分析层间离缝。张邦等[7]结合超声波方法和地质雷达方法联合检测轨道板沉降缺陷，取得了一致的效果。杨春[8]研究了分层物体的超声检测方法，使用合成孔径方法采集的小孔径数据，利用延迟叠加的方法合成大孔径以提高成像精度，但是使用小孔径采集模式无法得到混凝土结构的超声波速度，不利于精确成像。

1 层状结构常见损伤特征与检测方法

1.1 层状结构常见损伤特征

层状混凝土结构在服役过程中产生的常见损伤主要有各层状结构内部裂缝、断裂损伤以及层间离缝、脱空等。这些结构损伤具有隐蔽性强和尺度小的特点，肉眼难以发现。部分损伤如表面的裂缝可直接观察，但是其发育的深度无法直接测量。

以运营高铁无砟轨道为列，从上到下依次为轨道板(厚25 cm)、砂浆层(厚3 cm)、支承层(厚约30 cm)。运营过程中产生的层间离缝、脱空等缺陷尺度极小，通常只有数毫米，少数达到厘米级，且外部难以发现，而轨道板与支承层内裂缝尺度更小，往往不到1 mm。另外，混凝土结构内部成分复杂，钢筋密布，给缺陷的高精度检测带来了较大的挑战。

针对层状无砟轨道砂浆层不密实、脱空、离缝等缺陷，建立无砟轨道层间损伤数值模型(图1)，利用弹性波方程有限差分法进行数值模拟。

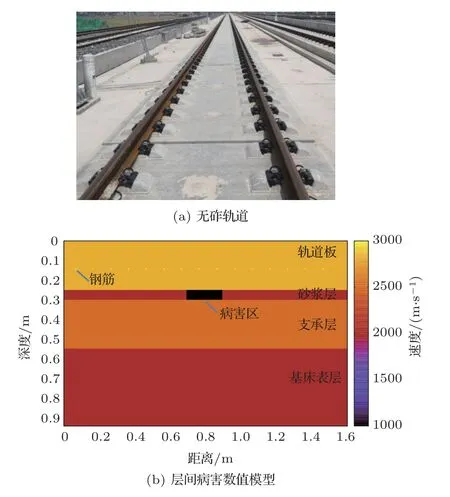
图1 无砟轨道与层间病害数值模型Fig.1 Ballastless track and numerical model of interlaminar damages

各类损伤模型以图1(b)所示的模型为基础，模拟不密实缺陷时，设置病害区横波速度为1000 m/s；模拟脱空时，砂浆层缺陷横波速度设为0 m/s；模拟离缝时，离缝区域速度为0 m/s，厚度为0.01 m，离缝分别出现在砂浆层顶部和底部。使用0.01 m规则网格对模型剖分，主频40 kHz 雷克子波作为声源，按0.01 m道间距进行数值模拟，不同缺陷模型模拟声压剖面如图2所示。

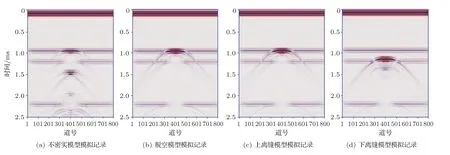
图2 砂浆层缺陷数值模拟Fig.2 Numerical simulation of defects in mortar layer

图2为砂浆层缺陷(不密实、脱空、离缝)数值模拟结果。图2(a)中，对于砂浆层松散缺陷，会在松散区端部产生绕射，低速松散区会导致砂浆层底部即支承层顶界面反射同相轴相对其他位置有延迟，且会产生多次波。图2(b)中，砂浆层灌注不饱满导致的脱空，会在砂浆层顶部产生很强的反射波，且超声波无法穿透脱空区域，导致下部支承层顶底界面无反射，同时，脱空区域两端也会产生绕射波。图2(c)为砂浆层顶部离缝模拟记录，离缝厚1 cm，与脱空(厚度5 cm)情况相同，由于超声横波无法穿透空气，此时离缝与脱空对超声横波产生的效果相同。当离缝在砂浆层底部时(图2(d))，离缝部位会产生较强的反射波，且离缝反射同相轴会比砂浆层底界面反射同相轴到时更短，离缝反射波会在砂浆层间多次震荡，能量逐次衰减。

1.2 超声波检测方法

超声波在混凝土结构中的传播机理复杂，会在混凝土内部石块、钢筋、裂隙、孔隙等内部阻抗界面上发生反射、散射、波场转换等，这种情况下，对混凝土结构内部微小的裂缝、离缝及脱空进行准确的探测难度较大。通常层状混凝土结构中的裂缝以及层间离缝等缺陷充填着空气或水等流体介质，而横波无法在流体介质中传播，因而对上述缺陷更为敏感。另外，横波相比纵波波速更低，波长更短，具有更高的分辨率。本文采用MIRA A1040型混凝土检测设备采集数据，该设备通过12通道换能器组成线性阵列，各换能器间距3 cm。换能器(图3)通过点接触硬耦合方式直接作用于检测面，探头尖端与轨道板表面接触点直径约1 mm，数据采集过程中无需使用耦合剂。超声换能器带宽为25～80 kHz，直接激发超声横波，通过接触点向检测对象发射和接收信号。

图3 超声点接触干耦合探头Fig.3 Ultrasonic point contact dry coupled probe

超声横波在无砟轨道混凝土结构中的传播速度范围在2600～3200 m/s，使用50 kHz 脉冲信号进行数据采集。在检测面上等间距布置测线、测点组成测网，测点间距为0.2 m，每个测点使用换能器阵列按如图4(a)示意方式采集半矩阵数据并进行TFM成像[9-10]。换能器排列从左到右，第1个探头发射时，其右边11 个探头接收信号，第2 个探头发射时，其右边10 个探头接收信号，阵元接收到的信号记为Rij，其中i为发射阵元编号(1 ≤i ＜N)，j为接收阵元编号(i ＜j≤N)。按此方式每个探头发射时，其右边所有探头接收信号，最终得到半矩阵数据，如图4(b)所示。

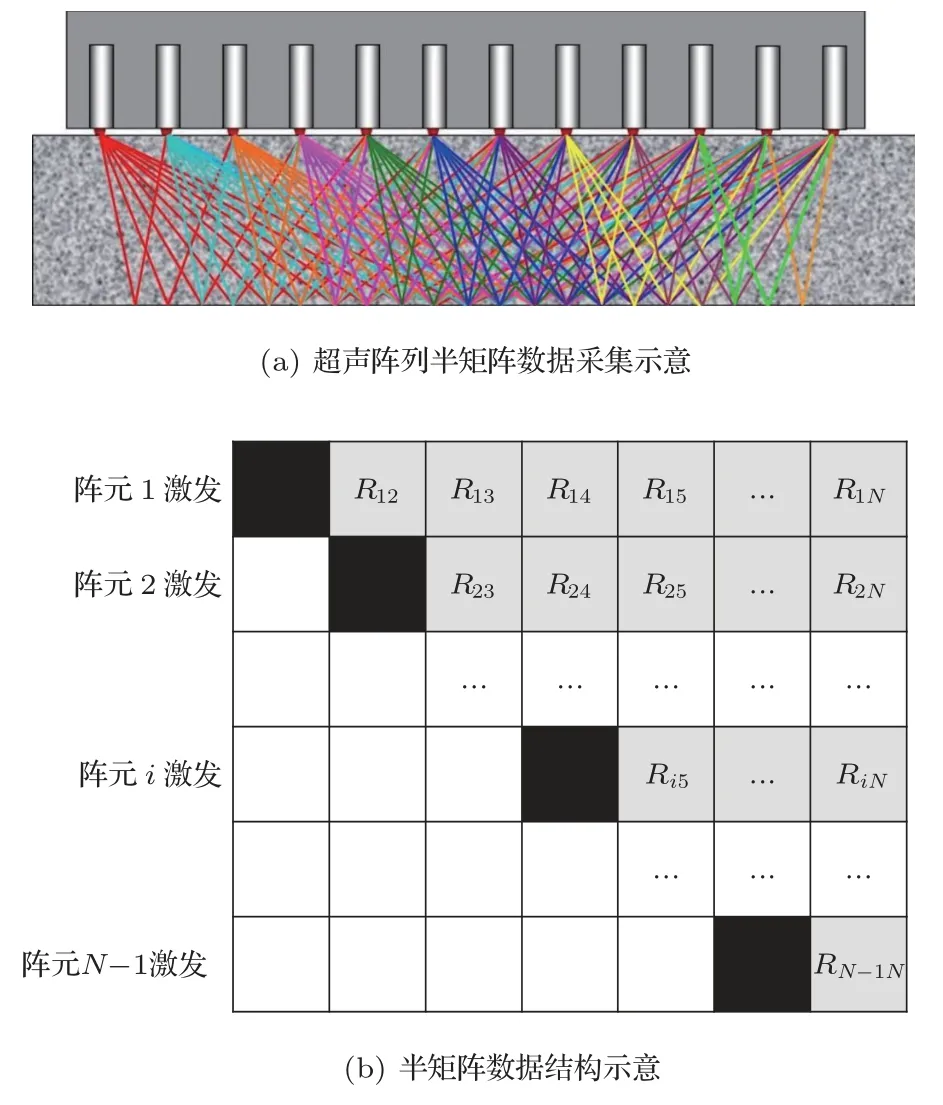
图4 超声阵列半矩阵数据采集示意Fig.4 Ultrasonic array half matrix data acquisition diagram

完成一次采集共可以得到66道数据，实现该线性阵列的半矩阵数据采集，如图5所示，图中超声直达波和反射波明显，蓝线为前两个探头激发时的表面直达波，红线为层状介质界面反射波信号。

1.2.2 课中讨论 A组（教改组）：（1）病例汇报阶段：在前期准备基础上，翻转课堂进行过程中小组抽签后对前期分发的病例进行讲解，包括对临床病史分析、检查方法的选择、影像学征象及鉴别诊断、治疗原则等进行简明扼要的讲解，其他小组学生进行评价和讨论，并记录问题，教师重点收集不同意见，观察学生讲解得情况及其余同学得讨论和交流情况；（2）教师指导阶段：教师对讲解小组进行点评，对课中阐述的重点、难点及疑点问题进行解答，并对延伸出的相关交叉学科知识点进行分析；（3）总结回顾阶段：组织学生根据讲解内容自行回顾影像资料，拟写出诊断报告并总结相关知识点、提出问题，教师根据提出的问题进行梳理并集中讲解。

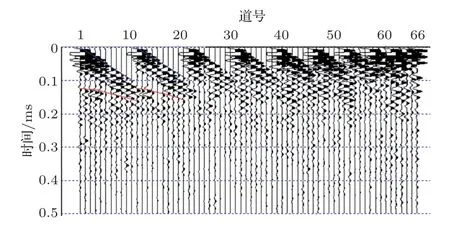
图5 超声阵列半矩阵记录Fig.5 Ultrasonic array common shot point gather

2 层状结构成像原理

2.1 TFM原理

对点接触换能器阵列采集的半矩阵数据，使用TFM 对层状混凝土结构进行成像。TFM 成像示意图如图6所示。

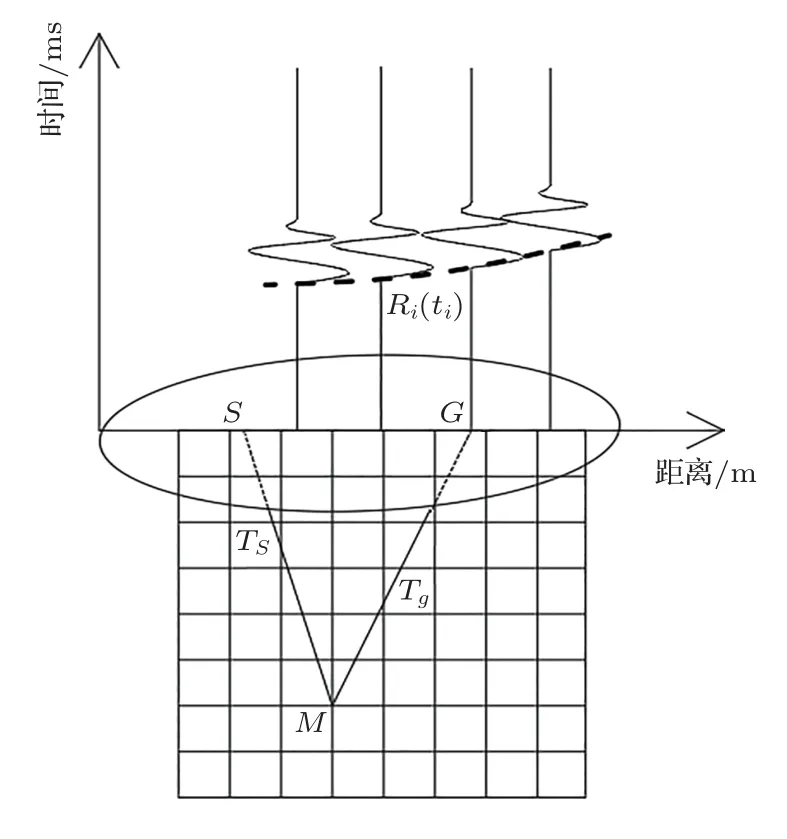
图6 全聚焦叠加原理示意图Fig.6 Schematic diagram of kirschhoffdiffraction superposition principle

对半矩阵中的单个回波记录成像时，记发射点为S，接收点G，则聚焦点为M的成像幅值SM为

式(1)中，Rij(ti,j)为半矩阵数据中第i/j个探头对激发/接收到的信号，其中ti,j为发射点S到聚焦成像点M最短传播时间tS和成像点M到接收点G的传播时间tG之和。对单一混凝土介质，ti,j的计算可通过距离除以时间得到；但是对于层状混凝土结构，进行精确成像需要得到超声波在各层混凝土结构中的传播速度v，和成像点到激发和接收点的传播路径以及最短时间tS、tG。

2.2 最短时间计算

超声波在上下速度存在差异的层间介质中传播时会产生折射现象，可使用射线追踪计算超声波在层间传播的最短时间，以及对应的路径。利用LTI方法计算超声波在层状轨道板结构中传播的最小时间与路径。

如图7 所示，对于任意两点A、B和成像点C，其坐标为(xa,za)、(xb,zb)，已知激发点O到A、B两点的声波到达时间ta、tb，假设超声波射线从A、B间的点D(xd,zd)传播到达点C。根据最短时间原理，可求得点C的最短到时公式[11]为

图7 由A、B 两点时间插值求C 点时间的几何关系Fig.7 The geometric relation of time at C is obtained by interpolation of time at two points A, B

式(2)中，|AB|、|AC|分别为AB两点和AC两点间距离，φ为AB、AC之间的夹角。

LTI方法通过网格剖分的方法计算超声波在结构物内部传播时间，同样适用于任意已知复杂结构。图8 为利用射线追踪方法模拟得到的超声波在层状无砟轨道结构中的传播路径与等时线图。模型长1 m，从上到下为轨道板、砂浆层、支承层，厚度分别为0.25 m、0.05 m、0.3 m，横波速度分别为2700 m/s、2000 m/s、2500 m/s，换能器在(0.2,0)激发。图8 中实线为超声波向下传播的最短时间等时线，虚线为支承层底反射波等时线，折线为部分接收点的传播路径。换能器激发信号后，超声波向下传播，遇到砂浆层和支承层时由于速度差异，波前面形态发生变化，沿波前面法线方向为超声波射线路径，当入射角较大时，在波阻抗界面处发生偏折现象。

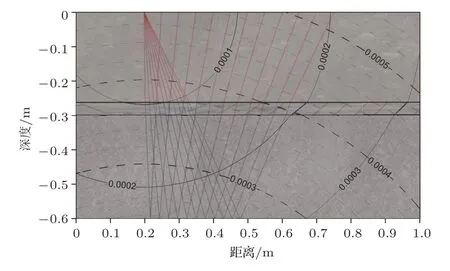
图8 层状轨道板超声传播最短时间与传播路径Fig.8 The shortest ultrasonic propagation time and propagation path of layered track plate

高铁无砟轨道板和支承层由于设计的混凝土标号不同，声波速度存在较大差异，成像前对不同混凝土结构层上进行波速测试，得到各层超声波速度v。利用公式(2)计算发射点-成像点-接收点最短到达时间时，先对成像区域进行网格划分(如图6 所示)，用网格点代表成像点，对每一个回波记录，利用无砟轨道现场实测的速度值，可以精确地计算成像点到激发和接收点的传播最短时间tS、tG，带入TFM成像公式(1)即可得到成像点幅值。

3 层间损伤定量分析

超声波在层状混凝土结构中传播，经过层间界面时，层间接触状态的差异会导致超声波在结构面反射能量不同，当出现离缝、脱空时，反射能量会显著增强。使用TFM 可对层状无砟轨道混凝土结构进行准确成像，但是对混凝土层间状态的评价只能根据反射面成像的能量幅值定性分析。本文基于超声波反射波信号和直达波信号进行能量特征分析，计算界面密实度指标。

用超声反射波能量来评价无砟轨道结构层间状态，要考虑在探头与检测面接触耦合的一致性问题，即采集数据时部分接收单元由于探头耦合较好，使得目的层反射能量相对较强，会导致离缝、脱空的误判。使用超声波沿检测面传播的直达表面波能量为基准分析反射波能量可有效避免该问题。

计算步骤如图9 所示。首先，对采集到的数据进行去零漂、滤波等预处理。然后，利用一个探头激发多个探头接收的信号表面直达波，计算轨道板速度值v及其对应的直达波累计参考能量A0。其次，根据速度v进行反射波校正叠加，形成叠后实测反射能量值为A(x,t)实测，其中x为测点位置，t为目的界面反射波传播时间。再次，根据能量扩散衰减理论，以表层参考能量A0为基础，计算目的界面反射能量参考理论能量幅值A(x,t)理论。最后，将实际叠后振幅取绝对值得到A(x,t)实测与计算出的参考理论能量值A(x,t)理论相除，获得密实指数Cf(x,t)：

图9 密实指数计算流程图Fig.9 Flow chart of compactness index calculation

式(4)中，α为衰减系数，v为速度，t为传播时间。在理论能量值计算过程中，超声主频为50 kHz，超声横波波长约为6 cm，大于混凝土轨道板内骨料颗粒直径，钢筋和骨料对超声波能量衰减不大，因此本文主要考虑扩散衰减系数αd和材料衰减系数αm(包含吸收和散射衰减)[12]。当频率为定值时，材料衰减率αm为定值，总衰减率α只和扩散衰减率有关，且为距离的函数[12]。α根据一点激发多道接收的表面直达波能量衰减情况近似计算。得到整个检测面的密实指数后，根据速度v将指数时间剖面由时间域变换到深度域，最终得到具有深度信息的密实指数深度剖面Cf(x,z)，其值越大表明密实度越高。

4 层状结构超声成像检测实验

4.1 结构内部裂缝检测

采用阵列式超声成像方法对轨道板结构内部的微小结构及裂缝进行检测时，可以适当提高检测主频，对轨道板上的裂缝进行精细检测。对轨道板裂缝进行检测时，采集阵列(换能器间距0.03 m) 横跨裂缝并以裂缝为中心点进行半矩阵数据采集，发射信号主频70 kHz，成像剖面如图10(a)所示，图中可清晰地看到轨道板结构内部的两层钢筋结构、轨道板底界面，剖面中存在从坐标(0,0)至(-0.1,0.2)斜向连续能量团，推测该裂缝为倾斜发育，深度0.2 m (如图10(a)中黑线所示)，该探测结果与从轨道板侧边观察结果基本相符。为确保探测结构的有效性，以裂缝为中心，将探测装置反转，进行重复探测，结果图10(b)所示，两次检测剖面有较好的重复性。

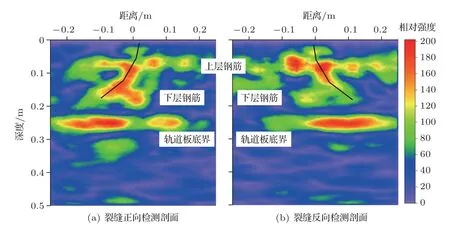
图10 无砟轨道板裂缝检测剖面图Fig.10 Section drawing of crack detection of ballastless track plate

4.2 层状结构检测

沿高铁层状无砟轨道方向布置测线，测线长度100 m，测点间距0.2 m，每个测点采集半矩阵数据。使用层状介质TFM和单一均匀介质TFM处理结果如图11所示，图11(a)为层状介质TFM成像结果，图11(b)为使用固定速度TFM 成像结果。图11中虚线为上层轨道板内钢筋层，实线为轨道板底界面，箭头所示同相轴为支承层底界面。由于轨道板超声波速度高于支承层速度，两者成像结果中，上层支承层结果基本一致，而支承层底界面成像结果则出现较大差别，如图中箭头所示，常速度成像结果中支承层底界面层位深度偏差较大，且成像结果不聚焦。

4.3 层间离缝检测

图12(a)为无砟轨道砂浆层泛浆情况，使用阵列式超声波方法检测层状无砟轨道的层间离缝时，在轨道板表面布置多条测线组成测网(图12(b))，线间距0.5 m，点距0.2 m，逐点测量。计算每个测点的密实指数，最终可得到三维密实指数Cf(x,y,z)，其中x、y为测点平面坐标，z为深度。取轨道板界面深度z=0.25 m，得到密实指数平面图(图13)，横坐标为沿轨道方向的距离，纵坐标为垂直轨道方向距离。图13 中密实指数小于0.8的蓝色区域对应轨道板侧边离缝泛浆发育范围。

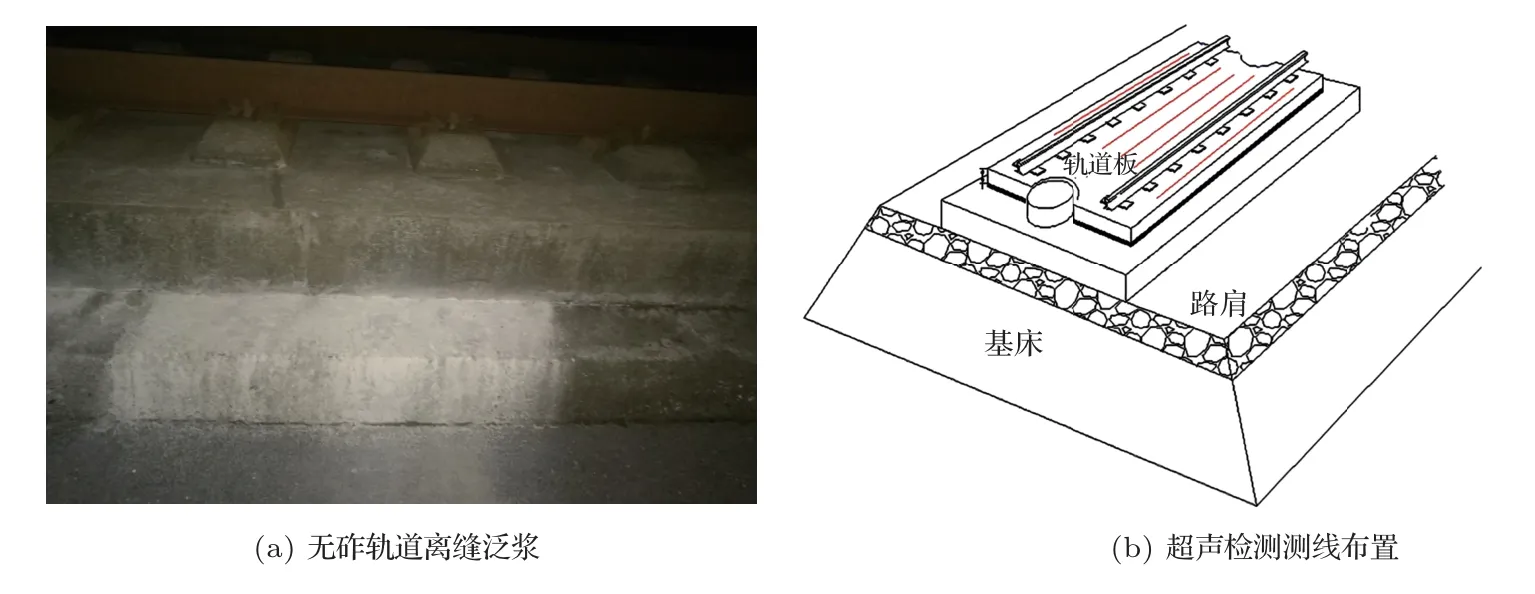
图12 无砟轨道离缝与超声检测测线布置图Fig.12 Ballastless track offseam and ultrasonic testing line layout

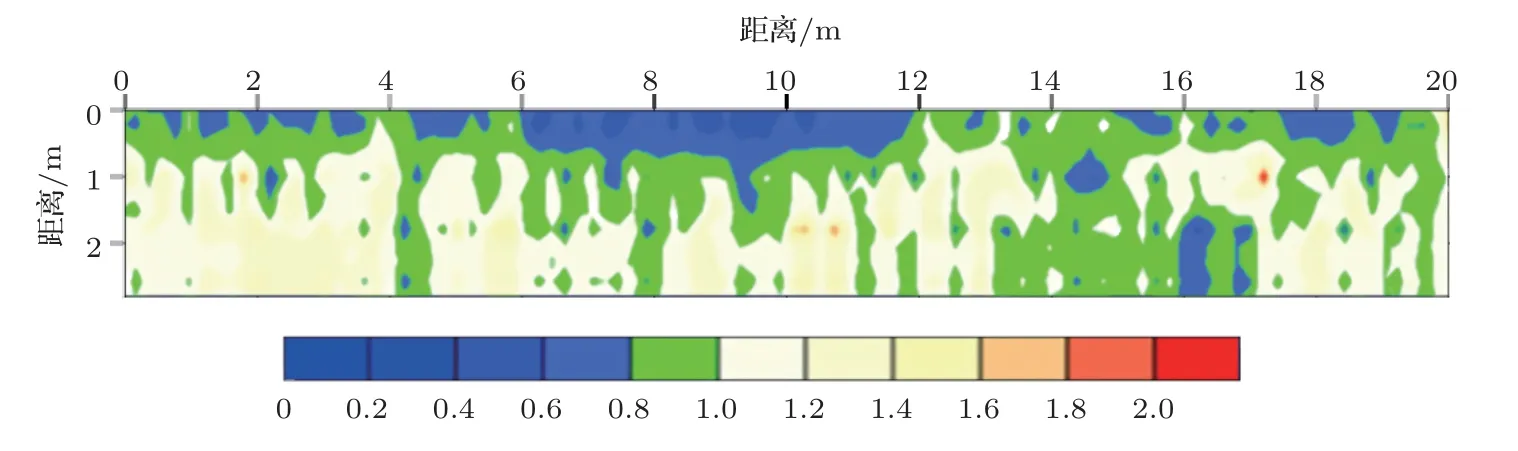
图13 轨道板密实指数平面图Fig.13 Plan of track plate compactness index

根据该结果在无砟轨道侧边布置等间隔的注胶孔，为避免轨道板上拱变形，采用低压(0.1～0.2 MPa)注胶的方式，将灌注胶注入无砟轨道板离缝(图14(a))。注胶从一端逐步向另一端进行，直到全部注胶孔注满注完。灌注胶在较小的压力下扩散充填离缝，最终的注胶量(图14(b)蓝色曲线)在侧边6～12 m 范围内明显高于其他位置，图14(b)中红色曲线为图13平面图中沿轨道方向左侧0.3 m处的密实指数曲线，与注胶量结果有较好的对应性，即密实度指数较低处注胶量较大。

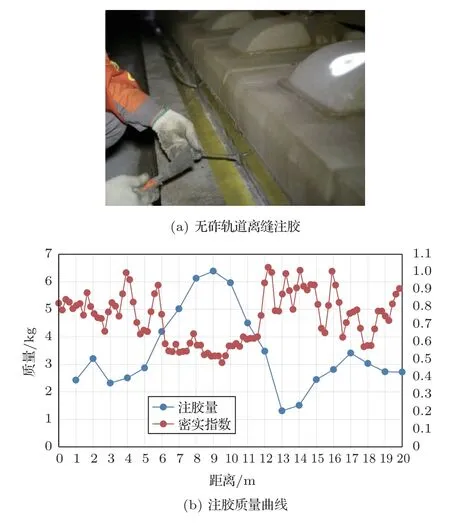
图14 轨道板离缝注胶及注胶量Fig.14 Amount of grouting for track plate

5 结论

本文针对层状钢筋混凝土结构层内裂缝以及层间离缝等损伤，使用基于超声横波的点接触阵列采集半矩阵数据，有效查明钢筋混凝土内部结构和裂缝。利用LTI射线追踪方法计算声波最短到达时间用于TFM 成像，相比单一介质常速度成像结果，具有深度准确、分辨率高、聚焦性好的优点。针对层间损伤，以超声直达波能量为基准，利用反射波能量计算密实指数，可定量分析无砟轨道层间状态。使用基于网格剖分的LTI 射线追踪方法提高超声TFM 成像精度对任意已知复杂结构内部高精度成像具有借鉴意义。