多波束测深仪姿态对测深影响分析及误差校正技术
2023-09-20杨海东
杨海东
(南昌理工学院 南昌 330044)
0 引言
多波束声呐产生于冷战背景。20 世纪60 年代,第一台多波束声呐由通用公司的哈里斯反潜作战部研制成功,并应用于美国海军绘制深海海图[1]。1976 年,第一台商用多波束测深仪SeaBeam 诞生。到20 世纪末和21 世纪初,多波束声呐蓬勃发展,在多个国家的大量科考船上得到安装和使用,目前在军用、民用领域都得到了广泛使用[2],其中国外典型的公司和产品包括Kongsburg 公司的Simrad 系列[3-4]、Reson公司的Seabat系列和T50-P等[5]。
在海洋测绘中,多波束测深仪是目前应用最广泛的设备之一,其主要功能是对海底地形进行精确测绘,在某些特殊场景中,也可以对海底大型物体(例如沉船、石油平台)进行三维扫描[6]。从工作原理上看,多波束测深仪利用T 型阵布阵、波束形成、底跟踪等关键技术,实现对海底地形的测绘。受到海上风浪和涌流的影响,多波束测深仪安装平台的姿态对测深精度和测深位置带来不利影响,主要表现在姿态变化导致测深仪波束指向或者阵列位置偏离了预期方位或位置,进而影响地形重建结果的质量,因此对多波束测深仪的姿态校正是提高其性能的重要方面。
许多学者对多波束测深仪姿态校正的方法进行了研究。赵建虎等[7]从动态吃水模型分析了姿态产生的因素,并给出了姿态对3 个方向上测量误差的影响表达式。阳凡林等[8]分析了姿态对水深测量的影响,利用横摇和横摇变化率的线性关系分解横摇姿态误差中的时延因素和尺度因素,并据此进行校正。王发省等[9]分析了全球导航卫星系统(Global navigation satellite system,GNSS)天线基线长度对姿态误差的影响,给出了多波束姿态误差和GNSS 定位误差之间的关系,验证了动态参考站差分(Moving base station difference,MBD)测姿结果可获得0.1°的姿态估计精度。Kiesel[10]、陈若婷等[11]先后提出了将发射阵设计为面阵,利用实时姿态数据反馈控制发射阵和接收阵的波束方向,使声呐在有姿态误差的情况下,发射和接收的主瓣始终朝向正下方的技术来解决姿态误差问题。
对当前多波束姿态校正文献的分析可以看出,当前多波束姿态校正的方法主要有两类:(1) 利用高精度姿态测量设备测量多波束实时姿态,并利用其对多波束的测深数据进行姿态补偿;(2)设计相控的发射阵和接收阵,将实时测量得到的姿态数据反馈至声呐的电路系统,通过电子波束控制保证声波发射和接收指向为声呐正下方。第一种方法是“后端”校正,是目前主流做法;第二种方法是“前端”校正,目前处于研发阶段,尚未得到商业化应用。本文在上述两类主流方法之外,提出了在平坦海底中利用测深数据快速估计主要姿态并进行校正的技术,该技术主要基于下列原理:在平坦海底条件下,测底数据的一些数学拟合特征可以较好地反演姿态的特性。
1 多波束工作原理及姿态类型
1.1 多波束工作原理
当前主流多波束测深仪采用一发多收的策略,其阵列布置为T 型的发射阵和接收阵,发射波束和接收波束在海底形成Mills交叉,在数据端进行电子波束形成后,获得声呐下方一定宽度范围内的波束图像,如图1 所示。之后利用底跟踪技术,获得海底线。利用声呐的移动,获得多条海底线后,通过定位、校正、插值等形成海底的深度面,从而获得海底地形图,为航道测绘提供技术支撑。
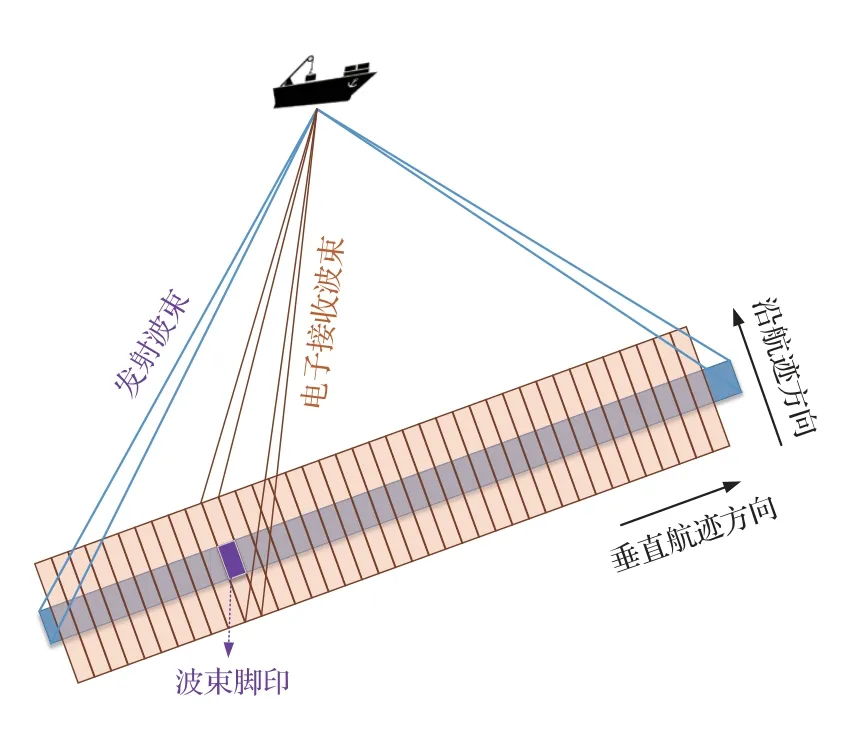
图1 多波束测深仪波束示意图Fig.1 Beam diagram of multibeam echo sounder
1.2 姿态类别及其对测深仪的影响概况
在利用多波束测深仪进行地形测绘的过程中,姿态校正是一个重要环节。这里主要有两方面因素:
(1) 多波束测深仪安装在船舶等平台上时,通常要在船舶中心线上安装姿态测量设备,典型的如光纤惯导,受到安装平台经常变动的影响,惯导的基准坐标系和测深仪的基准坐标系并不是平行的,因此需要对这两个坐标系之间的变换矩阵进行测量并校正,也就是“安装校准”。
(2) 由于多波束测深仪扫宽大,而其安装平台(通常是水面船舶)受到风浪和涌流的影响,存在6个自由度(3 个角度量、3 个位移量)的实时动态偏差,这对海底各散射脚点的准确估计带来不利影响。这就需要实时监测多波束测深仪的姿态信息,并补偿至其声呐图像中,也就是“姿态校正”。一般来说,前者是静态的、固定的,后者是动态的、实时变化的。多波束测深仪姿态校正通用方式是利用安装在平台上的高精度姿态仪,通过规划校准测线和后处理完成安装偏差估计,通过实时姿态数据进行动态姿态校正。
声呐平台在运动中产生了6 个自由度的姿态信息,包含3 个角度量和3 个线度量(或称位移量),3个角度量是艏摇(yaw)、横滚(roll)、俯仰(pitch),3个线度量是升沉(heave)、横荡(sway)、纵荡(surge)。6个姿态量各自含义如图2所示。
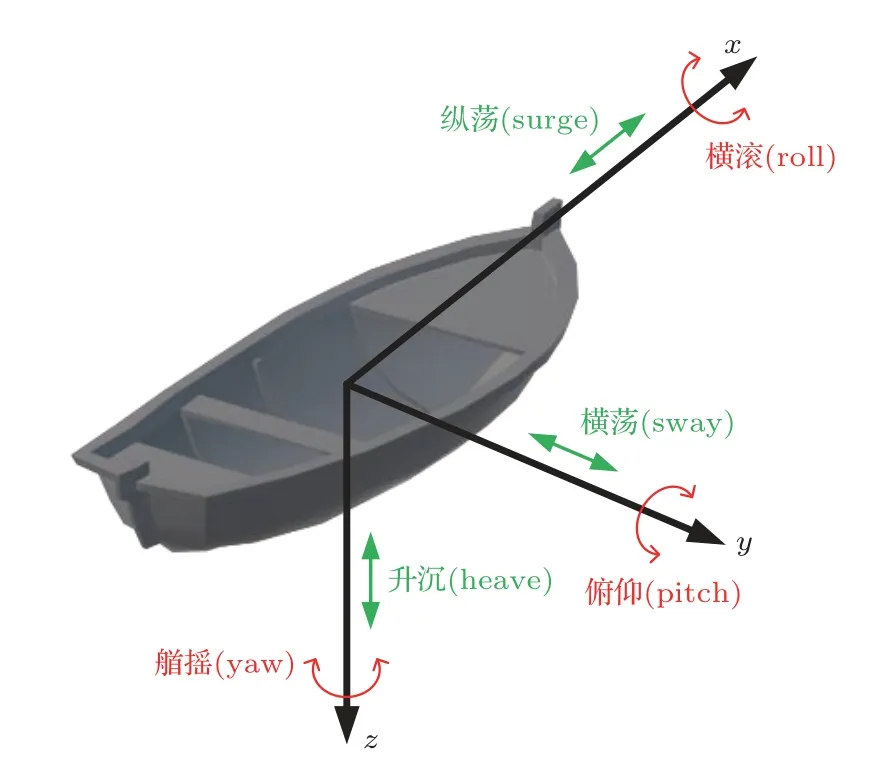
图2 声呐平台姿态示意图Fig.2 Schematic diagram of sonar platform attitude
声呐平台对多波束测深仪的影响因素包括水平面的定位影响和铅垂线方向的测深影响。根据几何关系不难得到6 种姿态对位置和测深影响与否的结论,如表1所示。
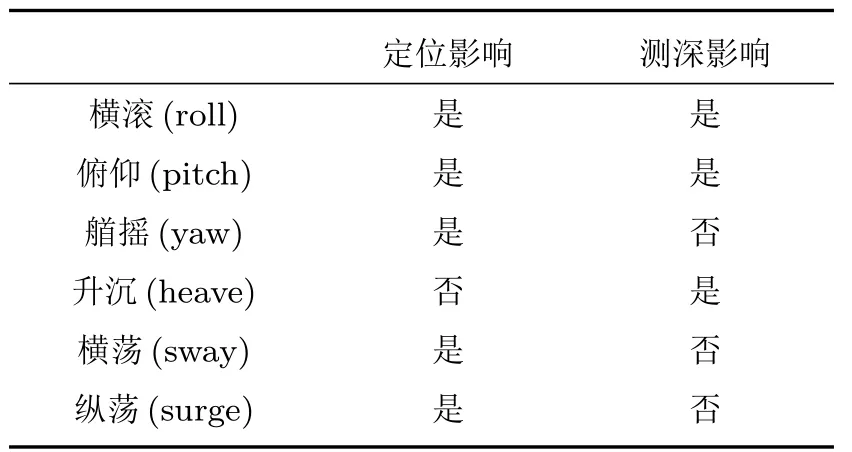
表1 姿态对定位和测深影响概况Table 1 Influence of attitude on positioning and bathymetry
本文仅讨论姿态对测深的影响以及对测深的校正,因此仅讨论横滚、俯仰和升沉等3种姿态。
2 姿态影响分析
2.1 理论分析
2.1.1 横滚(roll)
横滚对测深影响的几何示意图如图3 所示,设某个波束的波束入射角为θ,经检测底的斜距为r,则该点距离声呐的垂直高度为

图3 横滚(roll)对测深影响的几何示意图Fig.3 Geometric diagram of the influence of roll on bathymetry
引入横滚偏差θr后,该点的垂直高度为
定义横滚校正相对值并进行计算,有
其中,o(·)表示高阶无穷小。可以看出,由横滚角引起的相对偏差同时存在θr的一次方项和二次方项。
2.1.2 俯仰(pitch)
类似地,如图4所示,在俯仰对测深影响的几何关系中,有
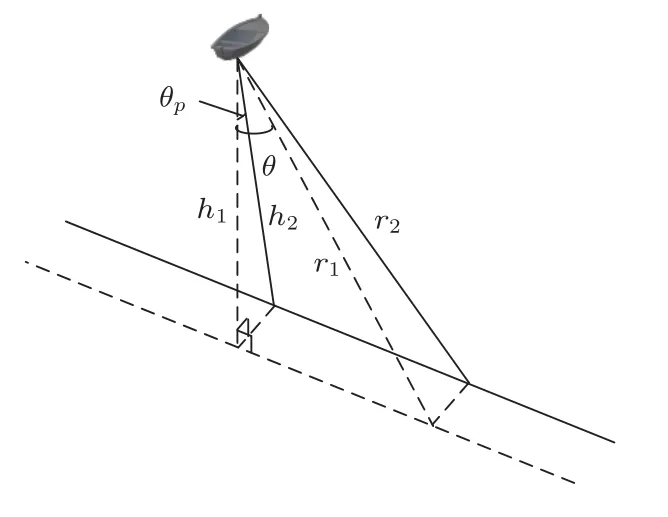
图4 俯仰(pitch)对测深影响的几何示意图Fig.4 Geometric diagram of the influence of pitch on bathymetry
可以看出,由俯仰角引起的相对偏差与θp的二次方相当,不存在一次方项。
2.1.3 升沉(heave)
升沉在z方向上产生位移,最终对测深结果产生影响。其对测深的影响表达式较为简单,设海底真实高度为h1,海底实测高度为h2,升沉为δh,则
通过实测海底高度数据h2拟合h1和δh的原理如下。海底变化所受到的地质运动、海流等影响因素的周期较长,而导致升沉的风浪、涌浪等因素的周期较短,因此h1是慢变量,其周期较长,而δh是快变量,其周期较短。根据上述分析,可对h2进行平滑滤波,将其快变的分量滤除后,即可获得慢变量h1。
滤波主要考虑滤波方法和滤波窗等参数。以平滑窗滤波为例,对滤波窗大小进行分析。设滤波器的阶数为2m+1,对输入信号x(n)进行平滑滤波后,输出信号为
利用傅里叶变换的性质,可以求得平滑窗滤波器的频率响应函数为
针对多波束测量中的升沉因素,考虑多波束的数据帧率为20 Hz,绘制不同阶数的频率响应如图5 所示。可以看出,平滑窗滤波器实际上是一个低通滤波器,并且随着阶数增大,其截止频率也逐渐变小。

图5 不同阶数平滑窗滤波器的频率响应Fig.5 Frequency response of smooth window filters with different orders
实际工作中,升沉具有一定的周期性,设升沉的频率为fh,为了对升沉进行有效滤除,规定主瓣在fh处的衰减达到-20 dB。据此通过数值计算的方式确定平滑窗的宽度。
举例来说,设升沉的周期为5 s,即频率为0.2 Hz,设声呐的数据帧率为20 Hz,则通过调整平滑窗的阶数,可以求得当阶数选择91 时,0.2 Hz 处的衰减可以达到预期的20 dB,如图6 所示。对于其他情形下的声呐数据帧率和升沉周期,可以通过上述数值计算方法,确定平滑窗的阶数。或者一种简易计算方法,可以计算一个升沉周期对应多少个采样点,以其采样点数附近的奇数作为平滑窗阶数也可。在上例中,一个升沉周期包含100 个采样点,则可以选择阶数为101。

图6 平滑窗滤波器(阶数91)的频率响应Fig.6 Frequency response of smooth window filter (91 orders)
2.2 仿真分析
为了说明横滚和俯仰对多波束测底结果的影响情况,进行仿真分析。仿真参数如表2所示。
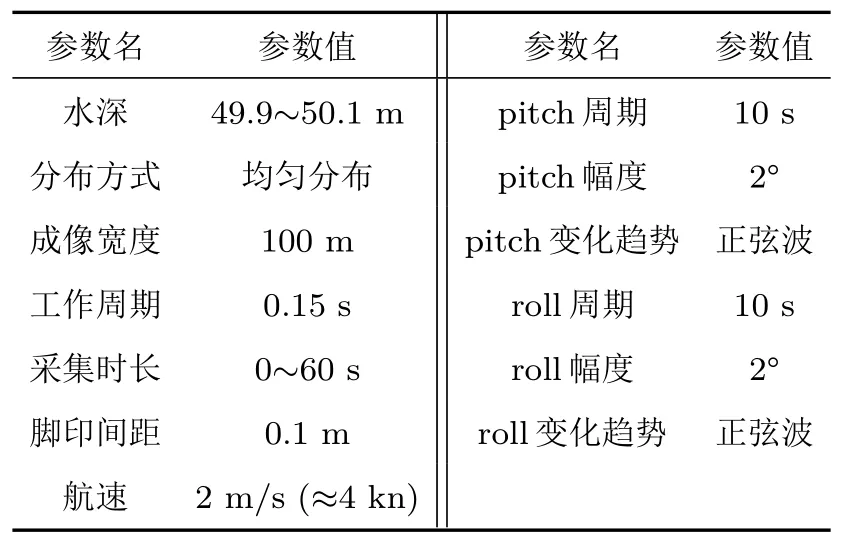
表2 仿真参数表Table 2 Table of simulation parameters
未加姿态影响的海底深度如图7所示。
图7 海深图(未加姿态影响)Fig.7 Bathymetric chart (without attitude’s influence)
单独加横滚姿态后,海深图如图8 所示。从图8中可以看出,声呐正下方影响较小,随着波束入射角度变大,海深偏差越来越大。

图8 加横滚姿态后的海深图Fig.8 Bathymetric chart with roll attitude
绘制不同波束角度条件下的姿态校正相对值如图9 所示,从图9 中可以看出,波束角度为30°时,相对值幅度达到2%;角度为60°时,相对值的幅度达到6%。
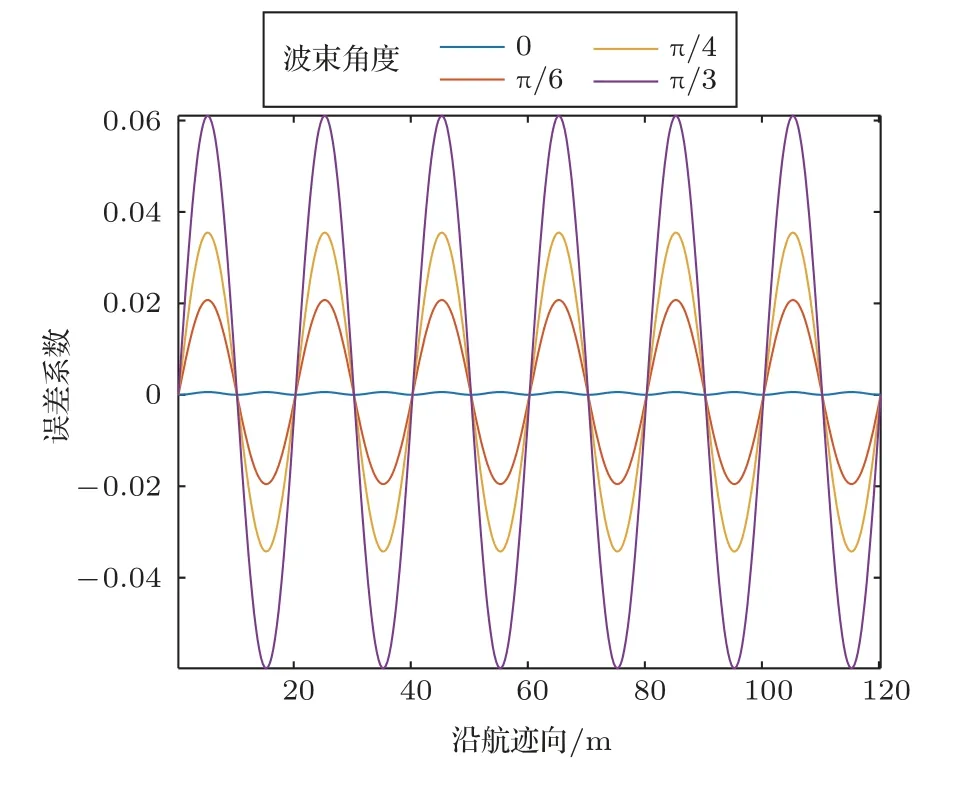
图9 不同角度下横滚校正相对值Fig.9 Relative value of roll calibration at different angles
单独加俯仰姿态后,海深图如图10 所示。从图10 中可以看出,在不同波束角度上的影响一致,且影响比横滚要小。

图10 加俯仰姿态后的海深图Fig.10 Bathymetric chart with pitch attitude
绘制俯仰姿态校正相对值,从图11 中可以看出,校正相对值的幅度约为3×10-4,远小于横滚姿态校正的相对值。
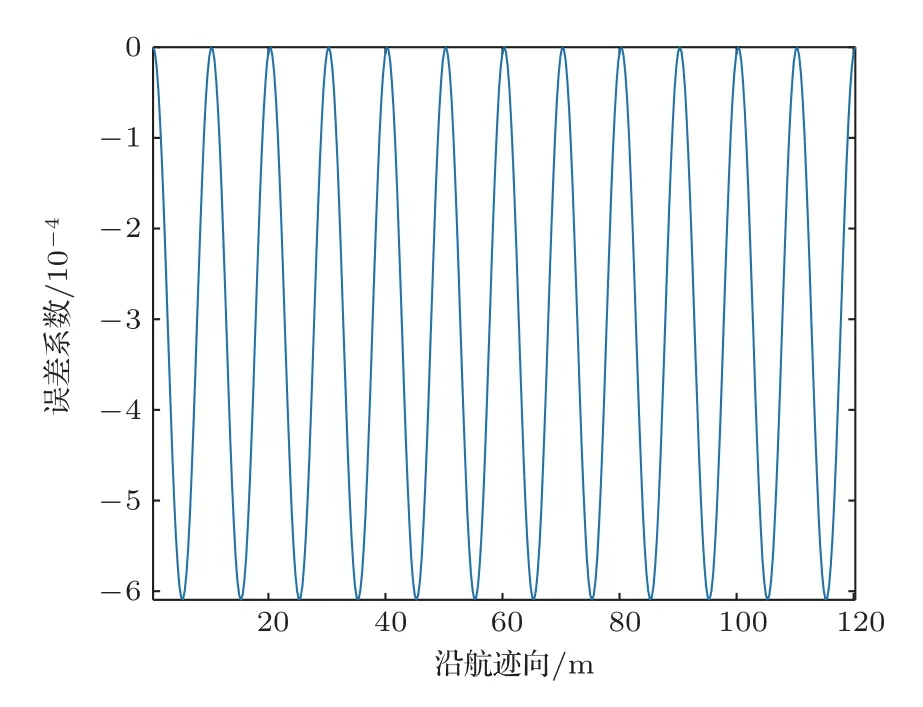
图11 俯仰姿态校正相对值Fig.11 Relative value of pitch attitude calibration
2.3 与国际海道测量规范对照
从横滚和俯仰引入的校正相对值来看,经过泰勒展开后可以看出,横滚会造成一次方项,而俯仰仅为二次方项。因此在横滚和俯仰数值相当的情况下,横滚角对测深的影响更大,俯仰角引起的校正值更小。
从仿真结果来看,当横滚和俯仰的幅度为2°时,横滚的影响远大于俯仰的影响,前者引入的相对偏差为百分之一量级,而后者引入的相对偏差为万分之一量级。
对于升沉姿态,当水深为数十米时,如果升沉的幅度在分米级,其引入的相对偏差也为1%量级。
国际海道测量组织于2020年更新了《IHO S-44海道测量标准》第6 版,其中对测深误差(标准中称为“垂直不确定度”)的最大允许值(TVUmax(d))定义为
式(12)中:a表示不随深度变化的部分;b为系数,表示不确定度中随深度变化的部分;d是深度。
该标准中对不同等级提出的要求如表3所示。

表3 海道测量规范垂直不确定度最大允许值Table 3 Maximum allowable value of vertical uncertainty in “IHO Standards for Hydrographic Syrveys”
对比表3 和仿真分析,在某些条件下,例如对测深精度要求为1%量级,或者角度姿态的幅度较小时,如果能够将横滚和升沉引入的测深偏差进行较好的校正,残余的俯仰引起的测深误差可以忽略。
3 基于测底数据姿态估计及校正
3.1 理论分析
经上述分析后,针对在平坦海底条件下,对横滚和升沉的校正,本文提出一种基于测底数据进行估计的方法。
在浅海测绘中,海底受到持续水流的冲刷,通常在局部范围内能够保持较好的平坦性。此时单次海底测线在没有横滚引入时,为水平线,而引入横滚姿态时,海底测线将为有一定倾角的直线。
设某一帧数据获得的海底测线在y方向的坐标为
其中,n为样本点数。
每个样本点上实际获得的距底高度为
引入横滚姿态时,距底高度估计ˆh应符合下列表达式:
式(15)中,θr表示当前帧数据的横滚姿态,h0为满足该表达式的一个常数。
利用最小二乘法对式(15)进行拟合,即设估计值与实测值之差的平方和为
当F(θr,h0)达到最小时的θr即为估计出的横滚角。利用拟合得到的横滚角对测深进行补偿,补偿方法是将样本点从笛卡尔坐标系转换至极坐标系,在极坐标系下补偿波束角度,再转换至笛卡尔坐标系下:
通过上述方法逐帧将海底数据的横滚进行校正。
利用校正后的测底序列估计升沉,基本方法如下。针对每个测底序列h(x,y),计算其中值,也就是在垂直航迹向(y方向)求其中值。多个测底序列的中值形成沿航迹方向(x方向)的海深线,该海深线是沿航迹方向的函数,记为d1(x)。
由于海底地形为“慢变”的,而升沉引起的海深偏差相比海底地形的慢变是“快变”的,因此对d1(x)进行平滑滤波后,更接近真实海底地形。设d2(x)为平滑滤波后的海底线,则升沉可以利用式拟合得到:
利用拟合得到的升沉可对海深矩阵进行升沉补偿,进而得到更真实的海底地形。
3.2 试验验证
为了对上述理论分析进行验证,获得了研究区的实测多波束数据,研究区内包括多条沟状地形特征,并且利用安装的光纤惯导同步获得了姿态数据。利用本节所述方法进行姿态估计后,与实测姿态进行对比,查看估计姿态与实测姿态的一致性。并利用估计的姿态对原始采集的海深数据进行校正,查看校正效果。图12 给出了一段范围约为100 m×120 m 的原始海底地形图。图13 给出了利用本文方法拟合和惯导实测得到的横滚角的数值。图14 给出了经过横滚校正后的地形图,与图12 相比,因姿态引起的地形纹波得到了一定程度减小。图15 是在图14 对应数据的基础上,利用本文方法拟合升沉数值,并给出惯导实测值进行对照。图16是进行升沉校正后的地形图,与图14 相比,地形纹波得到进一步抑制。
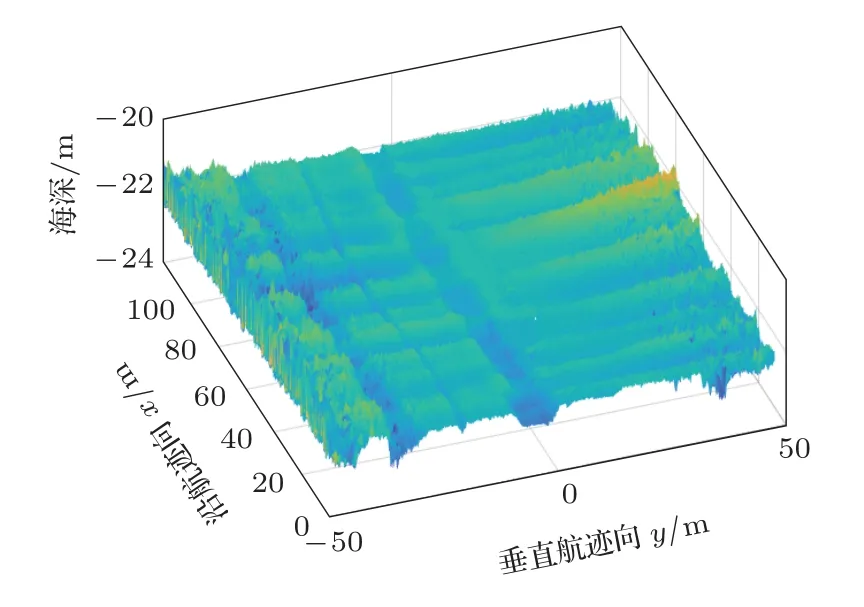
图12 原始地形图Fig.12 Original topographic map
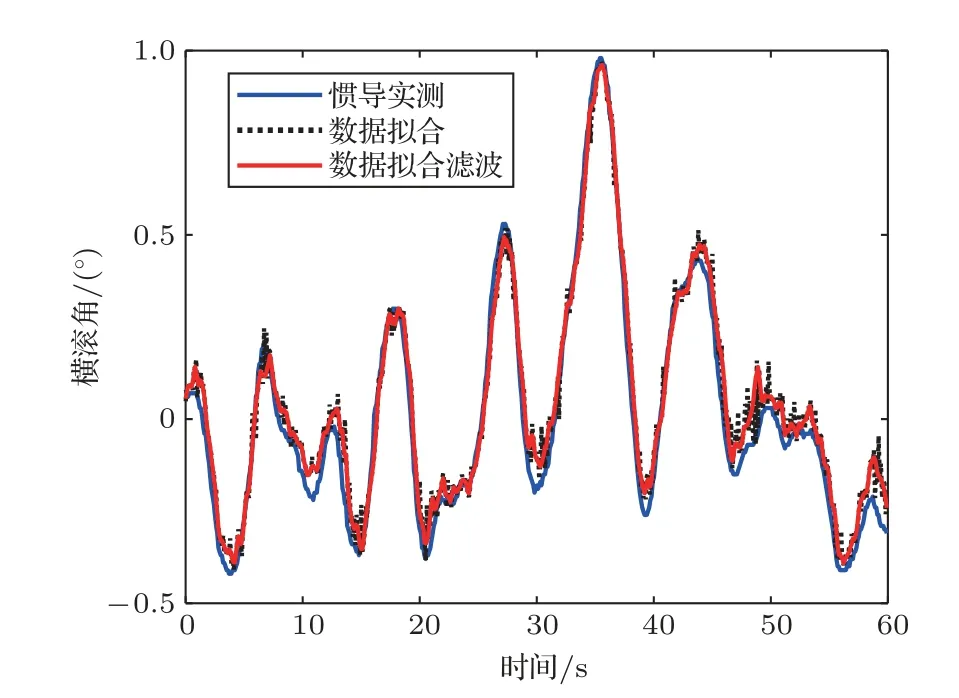
图13 横滚角实测值和拟合值Fig.13 Measured and fitted values of roll angle
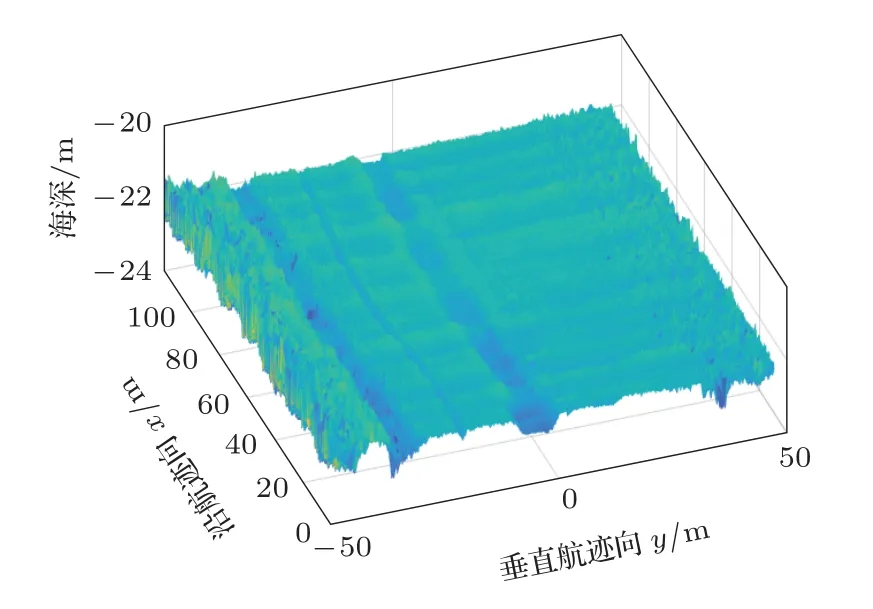
图14 横滚校正后地形图Fig.14 Topographic map after roll calibration
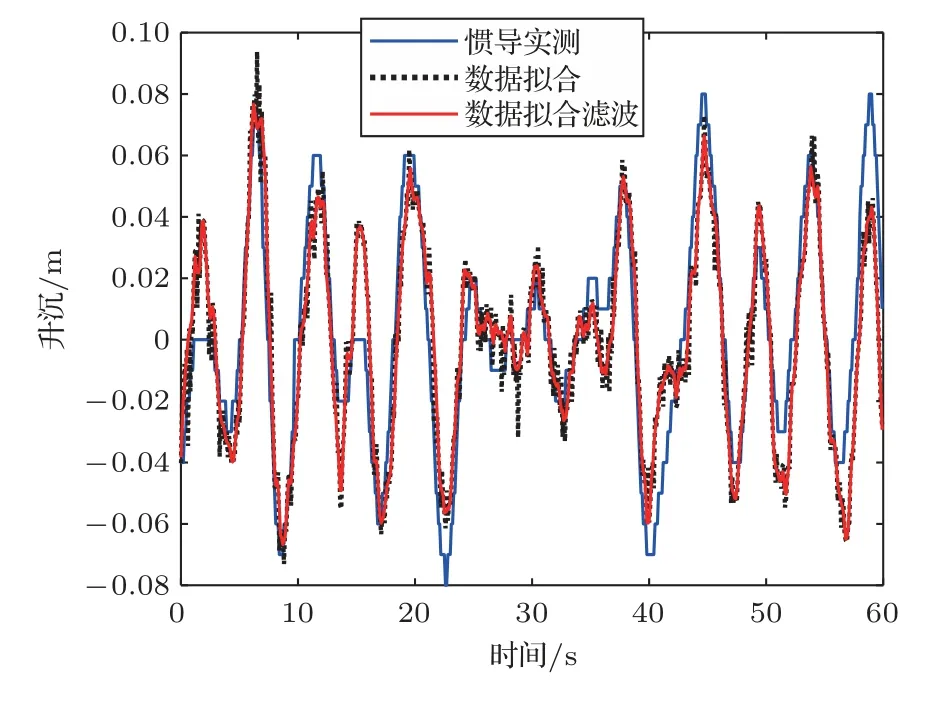
图15 升沉实测值和拟合值Fig.15 Measured and fitted values of heave
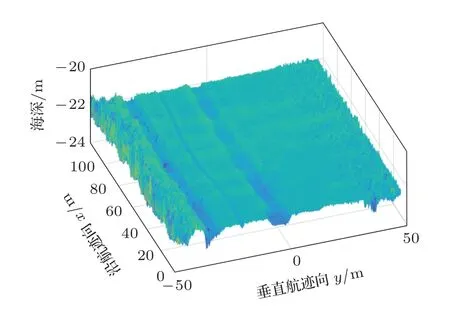
图16 升沉校正后地形图Fig.16 Topographic map after heave calibration
对数据处理进行定量分析如下。首先利用本文提出方法与惯导实测姿态进行对比分析,将惯导实测值视为“真值”,将本文提出方法计算值视为“估计值”,分析估计值与真值之间偏差的中误差。分析结果如表4所示,从数值可以看出,横滚和升沉的中误差与当前主流海洋测绘中惯导的测量精度处于同一量级。

表4 估计值与真值差值的中误差Table 4 Mean square error of difference between estimated value and true value
为了进一步说明本方法的效果,对地形点云数据的分布进行分析。在平坦海底条件下,点云数据受到海底不规则地形和测量噪声等多方面因素的影响,假设呈现正态分布。因此查看补偿前后点云数据正态分布的情况,如表5 和图17 所示,补偿前中误差较大,补偿后中误差减小。
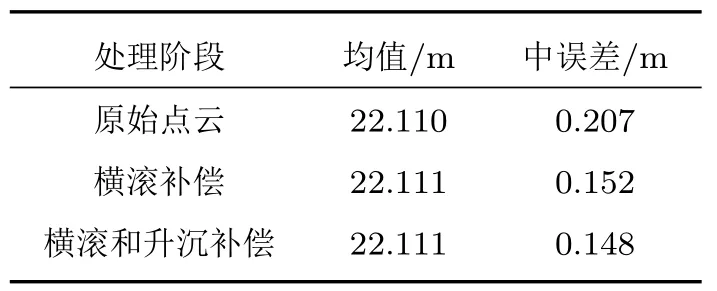
表5 不同处理阶段海深的均值和中误差Table 5 Mean value and mean square error of sea depth in different processing stages
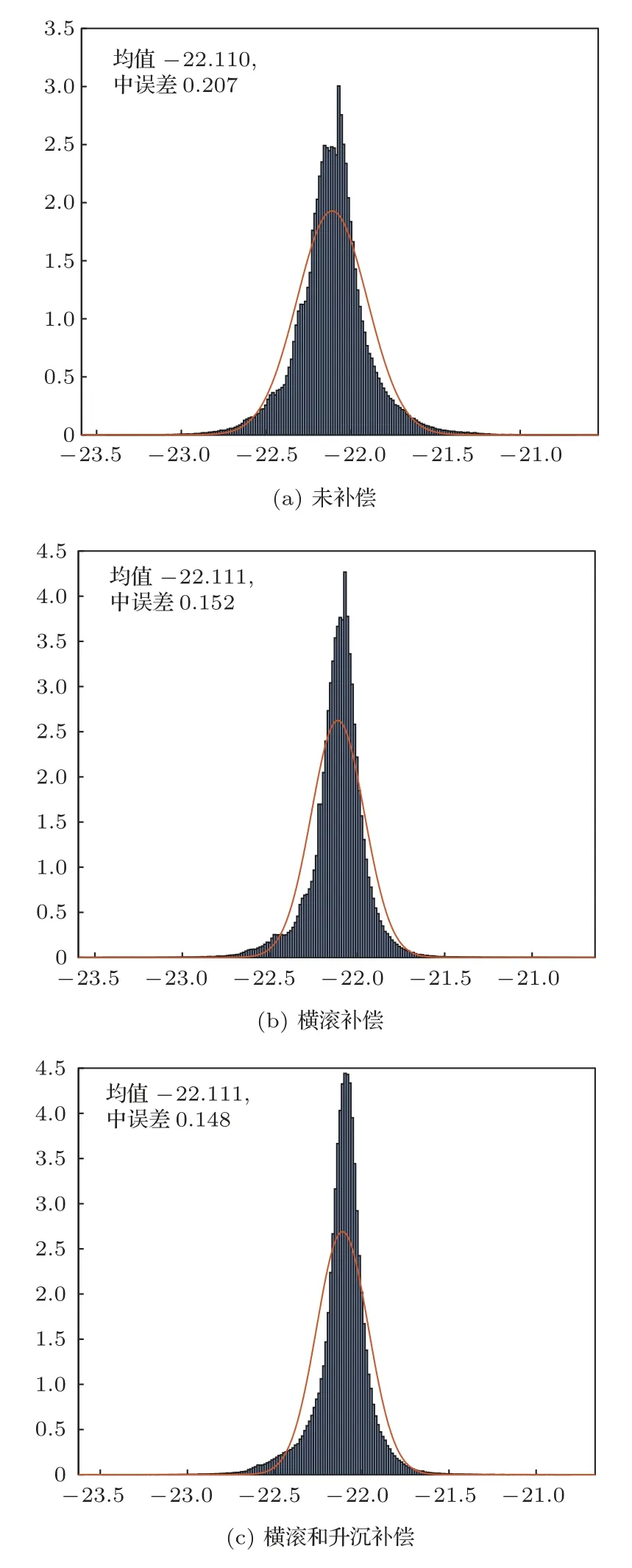
图17 深度直方图分布Fig.17 Depth histogram distribution
从上述处理结果可以看出,本文提出的基于测深数据的方法,估计拟合出的横滚和升沉与惯导实测值吻合度较好。
利用拟合的姿态对地形数据进行补偿后,补偿效果较好。
4 结论
多波束测深仪是海底地形测绘的重要技术,姿态校正在多波束测深仪数据处理中具有重要意义。针对多波束6 自由度姿态对测深的影响进行了分析,通过泰勒展开,分析得到对测深影响最为明显的姿态是横滚和升沉,而俯仰对测深影响较小。
在平坦海底条件下,研究了基于测深数据本身特征对横滚和升沉进行估计的方法。对海试数据进行了分析,与惯导采集的姿态数据进行对比可以看到估计的数据的准确性较好。利用估计得到的姿态数据对地形数据进行校正,校正效果良好。
