基于MRMR-SSA-BP的PM2.5浓度预测模型
2023-09-20张一准颜七笙
张一准,颜七笙
(1. 东华理工大学地球科学学院,江西 南昌 330199;2. 东华理工大学理学院,江西 南昌 330199)
1 引言
随着世界范围内的经济和工业化的快速发展,空气污染的问题日益加剧,城市空气质量问题已经严重影响到居民的正常生活和幸福指数。2021年“十四五”开局之年,各省和地区相继推出生态环境保护规划,坚持以改善生态环境为核心,加快推动绿色发展,而空气质量问题是其中重点要解决的问题。PM2.5浓度是衡量空气质量的一项重要指标,我国早已于2012年在《环境空气质量标准》新增PM2.5检测指标[1],因此寻求精确预测PM2.5浓度的方法对“十四五”空气质量改善行动计划具有重大的意义。
目前PM2.5的预测方法主要有统计、数值以及机器学习等方法[2]。在统计模型中,如徐东等[3]基于多元线性回归模型对成都市PM2.5的趋势进行了预测研究,彭斯俊等[4]基于ARIMA模型对PM2.5的浓度进行预测,但预测精度有待提高,因为统计模型通常要求数据具有正态分布或平稳等特性,不适宜直接用于污染物浓度的预测[5]。数值模型是以大气动力学理论为基础,基于对大气物理和化学过程的理解,建立的大气污染度在空气中的输送扩散模型[6],如周广强[7]等基于WRF-Chem模式降水对上海PM2.5预报的影响预测,但是数值模型的准确性严重依赖于需要不断更新的排放源清单,预测地点的地理特点的复杂性以及污染物大气过程的复杂性都使得预测模型的实现复杂化[8]。而新兴的机器学习模型则在PM2.5浓度的预测上展现出更好的效果,如李志生[9]等根据多种树模型进行对比,确定LightGBM预测模型在其它树模型中训练更快,占用内存更少,准确率更好的优点,但LightGBM模型是基于偏差的算法,对噪点数据敏感,也可能会产生较深的决策树,从而导致模型过拟合,为了弥补单一模型的不足[10],许多学者开始尝试组合多个模型来对PM2.5浓度进行预测,例如李建新[11]等利用混合核函数(HK)对传统的支持向量机(SVM)模型进行改进构造的MRMR-HK-SVM模型预测PM2.5浓度,相较于原始的SVM模型,拟合程度较高,具有较好的泛化能力。
但在现有的PM2.5浓度预测模型中仍存在以下问题:
1)现有的预测PM2.5浓度的组合模型中,大多数模型都只是模型简单的叠加,第一个模型的输出作为第二个模型的输入进行预测,或者模型多线性排列,最后的预测结果累加求均值,并没有真正的提升和改善模型。
2)预测PM2.5浓度特征值的选取较为单一,例如黄婕[12]在对PM2.5浓度预测研究中仅以时空特征作为输入,没有考虑气象因子和其它污染物对PM2.5浓度变化的影响。在空气质量的预测研究领域中,LEE et al[13]选择了历史污染物和气象数据来预测空气质量,准确率得到明显的提升。方晓婷[14]等人研究结果表明气温,湿度,风速及风向对PM2.5浓度有较大影响。所以在现有的PM2.5浓度预测研究中,PM2.5浓度的影响因子考虑的不够全面。
3)PM2.5的影响因素众多,每个影响因素对PM2.5浓度的影响都不相同,有的因素对PM2.5浓度变化的关系密切,有的因素对PM2.5浓度变化无明显交集,现有研究总是把所有的影响因素作为模型的输入来进行仿真预测,难免会对最后的结果造成较大的误差。
综上,本文选择了适合求解内部机制复杂问题的BP神经网络作为基础模型,用麻雀搜索算法优化BP神经网络的初始权值和阈值,提高BP神经网络训练的速度和精度,用最大相关最小冗余算法从从历史污染物和气象数据PM2.5、PM10、SO2、NO2、CO、O3、风向、平均气压、风速、平均气温、相对湿度等11个影响因子提取出最优影响特征值作为模型的输入,构建成MRMR-SSA-BP模型,该模型能有效的弥补现有研究的不足和缺点,为PM2.5浓度预测提供了一种新方向。
2 研究区域和数据
2.1 研究区域
济南市位于山东省的中西部,南依泰山,北跨黄河,地处鲁中南低山丘陵与鲁西北冲积平原的交接带上,地势南高北低,导致热岛效应严重,风速小,污染物不易于吹散。因为城市经济发展,燃煤烟尘,工业粉尘和垃圾、风沙及车辆行驶的扬尘日益增多,导致济南市的空气质量在发布质量周报的城市中长时间居于倒数十名内。在2019年更被生态环境部评为环境质量较差城市之一。
2.2 数据来源
本文的历史空气污染数据来源于中国空气质量在线监测分析平台(https:∥www.aqistudy.cn/historydata/about.php),气象天气数据来源于中国气象数据网(http:∥data.cma.cn)。分别采集了2019年1月1日至2019年12月31日的PM2.5、PM10、SO2、NO2、CO、O3、风向、平均气压、风速、平均气温、相对湿度的数据。总共365组数据,所有数据均为日平均值。其中2019年1月1日至2019年11月30日为训练数据,2019年12月1日至12月31日为测试数据。
3 预测模型
3.1 最大相关最小冗余算法
最大相关最小冗余算法(Max-Relevance and Min-Re-dundancy,MRMR)最早由彭汉川[15]等提出用来提取最优特征值。可以使用互信息在特征集合中找出与结果相关性最大,并且特征之间相关性最小的特征[16]。因为PM2.5的浓度影响因素关系复杂,不排除本文选择的特征值(PM10、PM2.5、SO2、NO2、CO、O3、风向、平均气压、风速、平均气温、相对湿度)中有相关性。所以用最大相关最小冗余算法来去除可能存在的数据冗余。互信息可以理解为一个变量中包含的关于另一个变量的信息量。假设两个变量为X,Y则互信息为
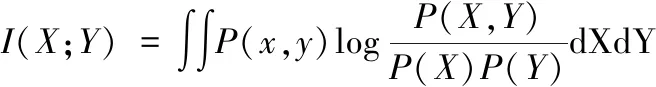
(1)
式中:P(X)和P(Y)是变量X,Y的概率密度函数,P(X,Y)是联合概率函数。由式(1)可得互信息I(X;Y)和互信息I(Y;X)是相等的。互信息度量了两个随机变量之间共有的信息量程度,这个值越大,两个变量之间的相关性越大[17]。
以互信息为基础,最大相关最小冗余算法可以根据最大统计依赖性准则来选择特征[18]。
MRMR算法的最大相关定义为

(2)
MRMR算法的最小冗余定义为

(3)
式中:S表示特征集合,c表示类别。I(Xi;c)为特征与目标的互信息,本文研究中表示的是11个特征值(PM10、PM2.5、SO2、NO2、CO、O3、风向、平均气压、风速、平均气温、相对湿度)和下一日的PM2.5的互信息,I(Xi;Xj)为11个特征值之间的互信息。
MRMR的特征选择标准为
信息差
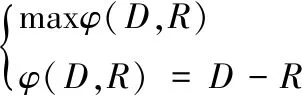
(4)
信息熵

(5)
式(4)是常用的整合准则方式,故本文用式(4)整合优化[19]。
3.2 麻雀搜索优化BP网络神经模型(SSA-BP)
3.2.1 麻雀搜索优化算法
麻雀搜索优化算法(Sparrow Search Algorithm, SSA)是由薛建凯[20]在2020年受麻雀觅食行为和反捕食行为提出的,该算法收敛速度快,寻优能力强。该算法的原理是在把麻雀分为发现者和追随者,发现者本身适应度高,搜索区域广,在整个种群中负责搜索有丰富资源的区域。追随者为了获得好的适应度,追随者利用发现者来获取资源。当整个种群面临捕食威胁时,会立即进行反捕食行为,发现者和追随者身份可以动态变化,但是所占种群数量的比重是不变的[21]。在SSA中发现者会优先获取资源,因为发现者负责整个麻雀种群寻找资源并为追随者提供方向。因此发现者的位置更新描述为
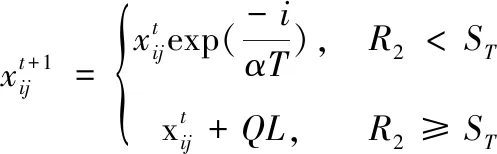
(6)
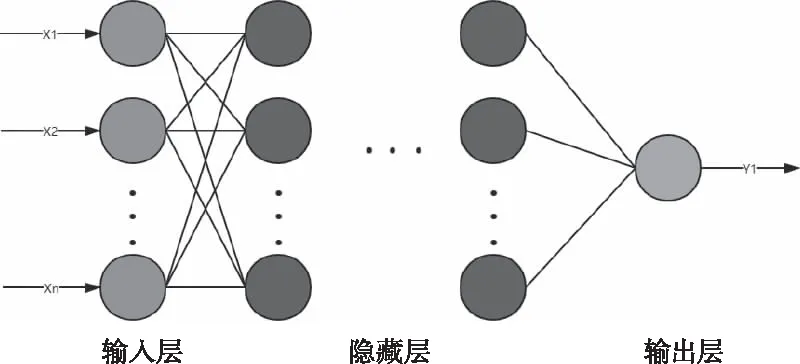
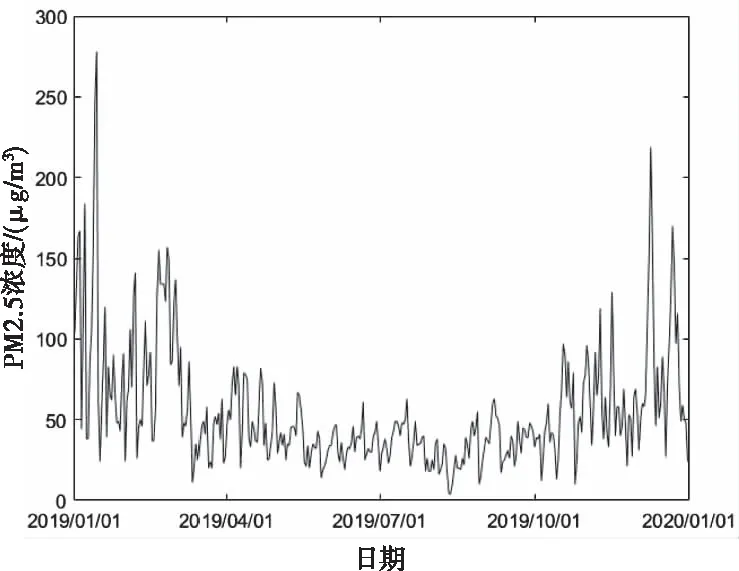
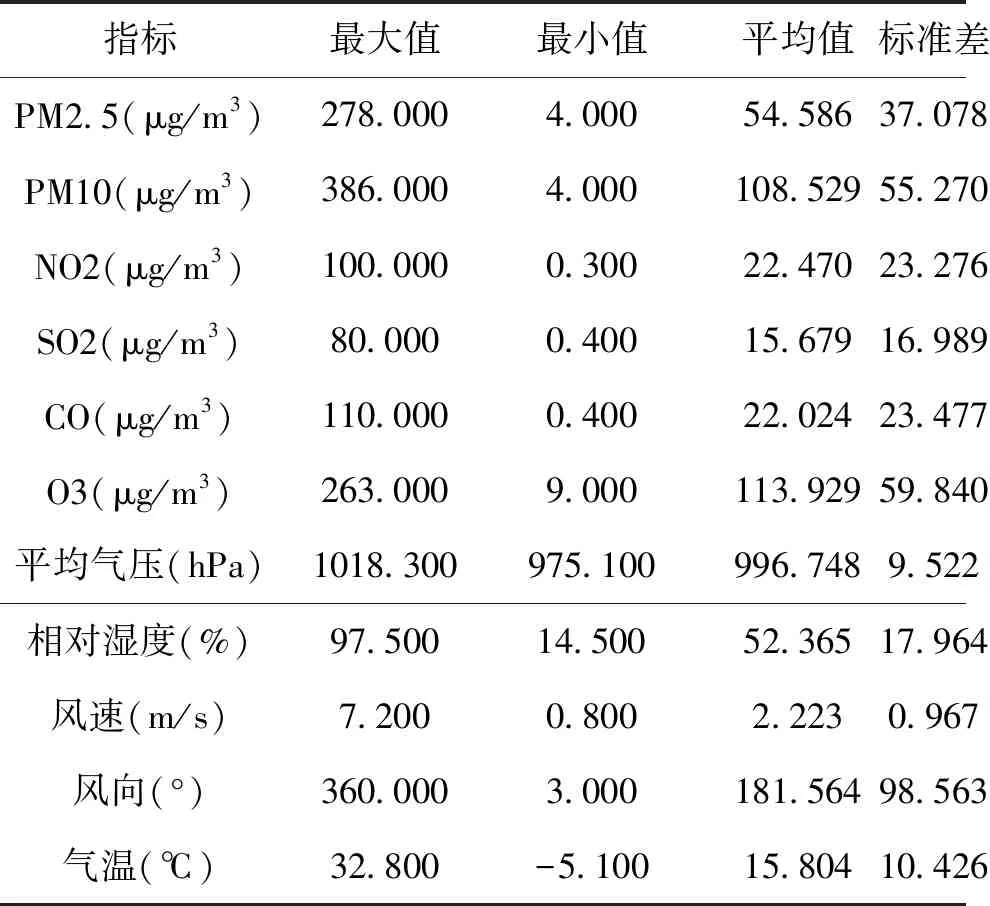
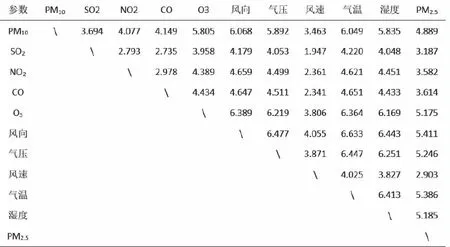
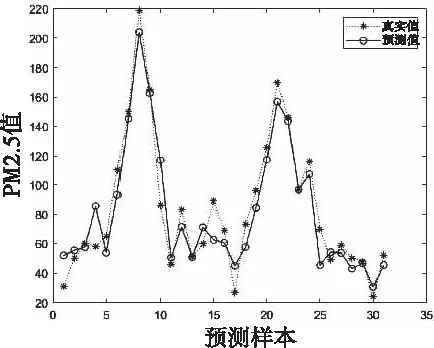
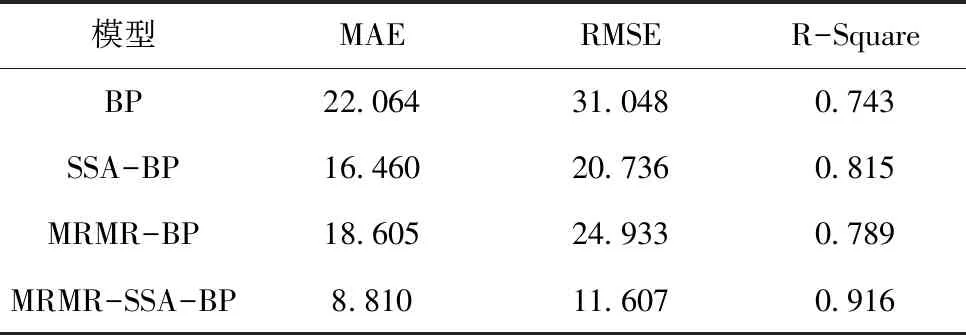
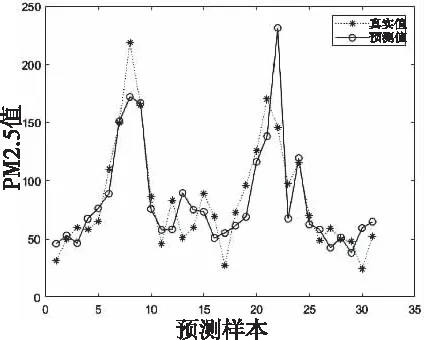
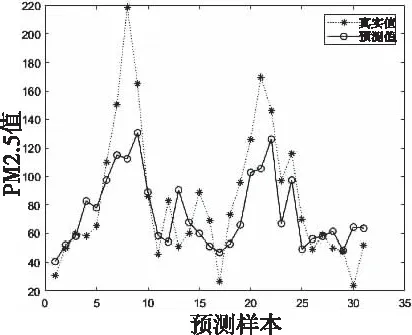
式中:t是当前迭代次数;T为最大的迭代次数;α为(0,1]的随机数;Q为一个正态分布随机数;R2和ST分别为预警值和安全值,预警值和安全值分别属于[0,1]和[0.5,1]。当R2 剩下的麻雀为追随者,为了获取好的适应能力,其位置公式为 (7) 式中:A是一个1*j的矩阵,A+=AT(AAT)-1;XP是发现者在t+1这次迭代时的最优位置,XW是当前最差的位置。当i>n/2时,种群收敛时符合标准正态分布随机数,值会收敛于0,表明适应度值较低的第i个追随者没有获得食物,处于饥饿状态,需要转移地点[22]。i<=n/2时,为当前迭代时的最优位置加上该麻雀与最优位置的每一维距离加减,将总值均分。即为在最优位置附近随机找一个位置,每一维距离最优位置的方差将会变小。 当面临危险时,麻雀会进行反捕食或者撤回,位置更新公式为: (8) 3.2.2 BP神经网络 BP神经网络(Back Propagation Neural Network,BP)是反向传播神经算法。原理是一种基于误差反向传播的多层网络。凭借其复杂模式分类能力和多维函数映射能力取得广泛的应用,BP神经网络分为输入层、隐含层和输出层,采用经验风险最小和梯度下降法来调整权值和阈值计算最优值[23]。 图1 BP神经网络结构 3.2.3 SSA-BP算法 为提高准确度,采用SSA算法对BP神经网络的初始权值和阈值优化来改善BP神经网络的性能。在本文的研究中为了提高BP神经网络的运算精度,隐藏层选择了三层。 基于MRMR-SAA-BP模型算法流程图如图2所示。 图2 MRMR-SAA-BP模型流程图 1)收集济南市的气象数据和历史污染物数据,预处理数据,把因为机器故障缺少的数据,用相邻两日的平均值填充。因为特征值中不同特征取值范围相差较大,对数据进行归一化处理,提升训练速度。 2)通过最大相关最小冗余算法特征选择选出最优的特征子集。根据式(1)算出各项特征值之间的互信息和各项特征值与目标值的互信息。根据式(2)算出特征值与目标值得最大相关性,式(3)算出特征值之间相互的冗余。最后根据式(4)作为整合准则,选出最优的特征子集。 3)确定BP神经网络的拓扑结构。为了提高BP神经网络的运算精度和运算速度,选择合适的隐藏层节点数和层数。 4)根据麻雀搜索优化算法算出适合初始权值和阈值。首先初始化种群和迭代次数,根据式(6)更新发现者的位置描述,为追随者提供觅食方向。追随者为了获得更好的适应度,根据式(7)更新位置,同发现者争夺食物,或围绕在发现者周围觅食。当麻雀的适应度较低,处于种群边缘,容易受到攻击,所以根据式(8)fi≠fg一行,调整位置来躲避攻击,而处在种群中央的麻雀会根据式(8)fi=fg一行,去接近它们相邻的同伴,来尽量减少它们的危险区域。因为适应度越大,得到的优化参数解最优,把相邻GAP代种群的距离小于可接受的最小距离作为判断是否终止的准则,不再依赖最大进化代数,能自动识别[24]。 5)BP神经网络获取参数,在归一化的训练集上训练得到预测模型。 6)把归一化的测试数据输入到预测模型中,得到预测结果,计算出结果的平均绝对误差,当平均绝对误差值小于预设值时为符合要求,输出结果;当平均绝对误差值大于预设值时,重新执行4) 5)计算出BP的权值和阈值进行预测,极大的预防了模型陷入局部最优解的情形。 7)最后根据式(9)(10)(11)算出均方根误差,平均绝对误差,R-square来进行模型评价。 本文用3个评价指标来评估模型,分别为均方根误差RMSE,平均绝对误差MAE,R-square。数学公式为 (9) (10) (11) RMSE,MAE,当预测值与真实值完全吻合时等于0,及误差越大,该值越大。R-square是拟合优度的一个统计量。表示1减去y对回归方程的方差与y的总方差的比值,值越大代表数据拟合度越好。 济南的PM2.5时序图如图3所示,济南市的PM2.5呈现出两头高中间低的U型图像,在1月到3月和11月到12月PM2.5急剧升高。在夏季天气比较热时PM2.5浓度偏低,在冬季时PM2.5曾一度逼近300大关。图中可以看出PM2.5具有季节性分布的特点。贺博文[25]等研究表明,承德市的PM2.5浓度夏季减少的原因可能是因为夏季偏南方较强,加上较大的降水量很大程度上缓解PM2.5的污染,加上冬季的气候条件,导致排放增加,造成PM2.5浓度增加。所以风向是研究预测第二天PM2.5浓度的一个重要指标,所以本文研究中把风向放进了初始的11个研究指标当中。 图3 济南市PM2.5浓度时序图 由表1可知,济南市PM2.5浓度最低时达到了4 μg/m3,远远高出国家环境标准,可以从夏季和冬季的各项指标对比入手,找出夏季冬季PM2.5浓度差距巨大的原因,对PM2.5的管控治理具有现实意义。表1数据中除了风速的标准差较小,表示除了风速以外,其它的指标因子波动性较大,代表指标数值有高度复杂性。 表1 济南市2019年气象和大气污染物数据统计结果 本文对于PM2.5的预测确立了11个特征数据,但是各项特征不仅对PM2.5浓度有相关性,它们互相之间可能也存在紧密的关系。如果直接默认各项特征值之间相互独立而去预测PM2.5的浓度,可能会导致模型预测精确度的下降。互信息是两个变量之间统计相关性的测度,用于表示信息之间的关系。它们相关性越高则它们的互信息值越大。特征值之间的互信息如图4所示,根据图中的互信息,选出与PM2.5(后一天数据)相关性最大的五个特征值是风向,气温,平均气压,相对湿度,O3。但是不能只考虑相关性也得考虑特征之间的冗余度。根据MRMR算法得出最优特征值为:PM10,PM2.5,SO2,风向,气压。可以看出气温和O3相关性特别高,但是它没有被选入最优特征集,因为气温和O3对PM10也有极强的相关性,所以不能入选。证明MRMR算法有一定的合理性,考虑了数据的冗余度。 图4 特征指标之间的互信息 MRMR-SSA-BP模型预测PM2.5时,首先选用了MRMR选择的最优特征集(PM10,PM2.5,SO2,风向,平均气压)作为模型的输入,再根据麻雀搜索优化算法,算出BP神经网络的最优权值和阈值。根据2019.1.1到2019.11.30作为训练集,12.1号到12.31号为测试集,MRMR-SSA-BP模型的预测结果如图5所示。SSA-BP结果误差图如图6所示,根据SSA-BP模型的误差分析,在夏季时预测PM2.5准确度较高误差较小,但是到春,冬两季时误差增多,误差数值也变大。考虑到可能夏季和冬季对PM2.5浓度影响的因子权重在变化,在一整年中,所有的影响因子可能对PM2.5浓度的影响是处于一个动态变化的过程中,再者因为春冬两季北方天气转冷,北方城市会采取集体供暖,导致煤炭排放增加,PM2.5浓度预测的影响因子变得更加复杂,使得春冬两季对PM2.5浓度的预测精度降低。 图5 MRMR-SSA-BP模型预测结果 图6 SSA-BP模型预测结果 为了验证MRMR-SSA-BP模型的优越性,本文采用模型BP、MRMR-BP、SSA-BP来进行比较。采用相同的训练集和测试集,结果如图7-图9所示,模型评价指标如表2所示。从预测结果图来看MRMR-SSA-BP模型的预测效果最好,与真实值拟合度最高。其次是SSA-BP模型,可以看出MRMR算法选出的最优特征值是可以帮助模型提高预测精度。SSA-BP模型较普通的BP模型有了显著的提升,证明麻雀搜索优化算法找出最优的权值和阈值能使BP神经网络的预测提高精确度和拟合度。从预测结果图和三个评价指标中从表2所示各模型的评价指标与模型预测结果图所展示的结果一样,最优的模型为MRMR-SSA-BP模型它较基础的BP模型2种误差分别降低了13.254和19.441。R2也从0.743上升到了0.916。表明本模型具有很大的优势去预测PM2.5浓度。李建新[11]等人根据SVM为基础模型建立得MRMR-HK-SVM模型对赣州市的PM2.5浓度进行预测,MRMR-HK-SVM模型的RMSE为14.891,因此,总体来说本文提出的MRMR-SAA-BP模型对PM2.5有着更高的预测精度。 表2 模型评价结果 图7 MRMR-BP模型预测结果 图8 BP模型预测结果 图9 SSA-BP误差分析图 针对PM2.5浓度预测本文以BP神经网络为基础模型,根据麻雀搜索优化算法确立BP神经网络的最优初始权值和阈值,根据MRMR算法选择输入数据的最优特征值来对济南市PM2.5浓度进行预测,建立了MRMR-SSA-BP模型,该组合模型不是多个模型的预测结果求平均值,它优化了传统BP模型性能上的不足和缺点,根据预测结果和模型评价充分说明了MRMR-SSA-BP模型是一种高效精确的模型。 1)根据已有的研究成果,选择了PM10、PM2.5、SO2、NO2、CO、O3、风向、平均气压、风速、平均气温、相对湿度等11项特征值作为预测PM2.5的影响因子,虽然每个因子都对PM2.5有很强的相关性,但是特征值之间也会有影响。这样会影响模型的预测准确度。用MRMR算法不止考虑特征值之间的相关性,也考虑特征值之间的冗余,来提高模型的运算速度和预测精确度。 2)BP神经网络预测中,初始的权值和阈值都是随机确定的,这个初始的权值和阈值对神经网络训练有很大的影响,但是又没有办法准确的获得,所以运用麻雀搜索优化算法找到最优适应度值得个体,来确立最优的初始权值和阈值,来提高模型预测PM2.5的稳定性和准确性。 3)根据PM2.5的浓度时序图可以看出,PM2.5有着强烈的季节性规律,济南冬季时PM2.5浓度达到278μg/m3,夏季时有时只有4μg/m3,所以对于PM2.5的治理可以根据季节性规律来进行治理调整。根据MRMR-SSA-BP模型进行PM2.5浓度的预测,有很高的的拟合能力,和较为准确的预测度,为空气污染预测,和治理空气污染提供了新的思路和方法。 根据模型运行结果来看,虽然模型具有很好的预测能力,但是夏季和冬季的预测能力偏差较大,如图9所示,根据SSA-BP模型的误差分析,在夏季时预测PM2.5准确度较高误差较小,但是到春,冬两季时误差增多,误差数值也变大。考虑到可能夏季和冬季对PM2.5浓度影响的因子权重在变化,因为冬季北方城市开始集体供暖,煤炭燃烧增加,使得PM2.5的影响因子与PM2.5浓度变化的关系更为复杂。因此未来的研究中,可以把PM2.5浓度的预测进行分季节预测,把每个季节的影响因子进行处理,选出适合每个季节的最优特征值来进行预测,提高模型预测的精确度。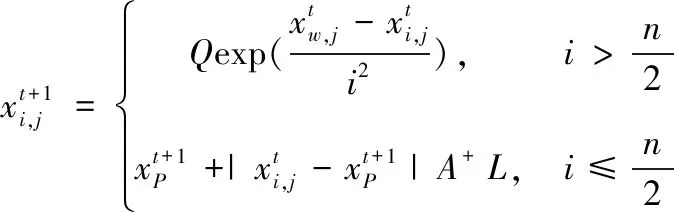

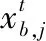
3.3 MRMR-SSA-BP模型

3.4 评价模型



4 结果与分析
4.1 济南市污染情况分析
4.2 基于MRMR算法的特征选择
4.3 MRMR-SSA-BP预测分析

4.4 模型评价
5 结论
