动态邻域粒化方式下的属性约简研究

邓安生,赵梓旭

(大连海事大学信息科学技术学院,辽宁 大连116026)

1 引言

粗糙集[1]是Pawlak提出的一种刻画不确定性的建模方法,但仅能用于处理符号型数据,对于数值型数据[15]而言,经典Pawlak粗糙集不能直接处理。为了弥补这一空缺,出现了许多粗糙集拓展模型[2-4,12]。其中基于邻域关系[14]的粗糙集拓展模型能有效的处理数值型数据。最近,邻域粗糙集在粒度计算[5,6]领域获得了大量的关注,相关的理论研究和方法被广泛应用于属性约简和特征选择[7,8,11,15]。

在邻域信息粒化方式中,通常是借助给定的半径来约束样本之间的相似性,最终确定邻域关系。在这个过程中可以看出半径的大小对最终的粒化结果起到十分重要的作用,若半径选取的过大,很有可能会导致不同标签的样本落在同一个邻域,引起信息粒化的不精确,不足以提供令人满意的判别性能。针对该现象,Liu[9]和Wang[10]等人提出监督邻域粒化策略,在邻域粒化过程中利用了样本的标签,使用两个邻域半径确定邻域关系。该策略可以在一定程度上减缓给定半径不合适时,导致粒化不精确的问题。然而,数据集中的每个样本都是不同的,所需粒化方式也理应是不同的,值得注意的是,该策略视数据集中的所有样本都是相同的,忽略了样本的特殊性;其次当样本量非常巨大时,每个数据集都要通过实验确定邻域半径会十分消耗时间。鉴于此,提出一种动态邻域粒化机制,具体首先根据样本分布初步计算邻域半径,降低因样本分布不均匀导致的负面影响;然后依据属性和标签的关系对第一步计算出的邻域半径进行缩减,以期能提高粒化的精准率,为每个样本设计一个独有的邻域半径;在此基础上给出上下近似算子,进而实现动态邻域粗糙集模型。

目前在基于粗糙集的属性约简方法中,都建立在粗糙集的上近似和下近似随着属性增加呈现单调性的前提下。若邻域半径是动态变化的,则上、下近似不再有单调性的特点。众所周知,下近似的单调性更有利于设置属性约简的迭代停止条件。因此,针对上文提出的动态邻域粒化策略,引入Zhang[13]等人提出的‘样本淘汰’(Sample Elimination)属性约简的方法作为本研究的属性约简策略,该策略在每次迭代选择属性时,仅考虑未被已选属性正确分类的样本,而那些已被正确分类的样本则会被淘汰,保证了下近似的单调性,并在此基础上提出一种多准则属性评估函数,缓解在约简的过程中产生的不一致的问题。

2 基础知识

2.1 邻域关系

给定一个决策系统DS=〈U,AT,d〉,其中U代表样本集合,AT代表条件属性集合,d代表决策属性集合。对于任意xi∈U且任意b∈AT,b(xi)表示在条件属性b下xi的取值,d(xi)表示在决策属性d下xi的取值,也就是通常意义的标签。U/IND(d)={X1,X2,…,XN}表示在决策属性d上诱导出的论域上的划分,∀Xi∈U/IND(d),Xi表示第i个决策类且1≤i≤N。

定义1:给定一个决策系统DS,∀b∈AT,邻域半径δ>0,在条件属性集B下的δ邻域关系定义为

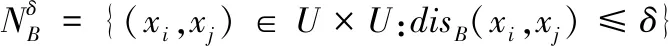
(1)

其中disB(xi,xj)表示在条件属性集B下两个样本之间的距离,为了简便起见,距离度量函数使用欧氏距离。

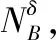
(2)

2.2 邻域粗糙集

定义3:给定一个决策系统DS,∀b∈AT,d关于B的上近似和下近似可以定义为

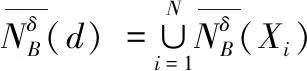
(3)

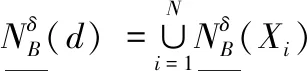
(4)

其中,∀Xi∈U/IND(d)。关于决策类Xi的上近似和下近似定义为

(5)

(6)

定义3中给出的上、下近似描述了目标概念的粗糙程度。为了反映出目标的确定程度,给出如下所示的依赖度(也称作近似质量)的概念。

定义4 给定一个决策系统DS,∀b∈AT,d关于B的依赖度定义如下

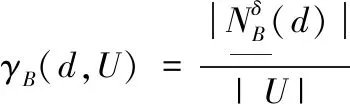
(7)

其中,|X|表示集合X的基数,U表示样本集。显然,0≤γB(d,U)≤1成立。γB表示根据条件属性B,确定属于某一个决策类别的样本在样本集U中的比例。γB的值越接近1,表示确定性程度越高,反之值越接近0,表示确定性程度越低。

3 动态邻域粒化机制和属性约简

3.1 动态邻域粒化机制

在传统的邻域模型中,邻域半径通常由实验分析给出且固定不变,这种粒化方式对有的样本粒化过粗,而对有的样本粒化过细,整体来看粒化效果并不好,所以需要对每个样本找到它适合的粒化方式,也就是适合它的半径。首先根据不同的数据分布初步为每个样本选择半径(下文简称为‘分布半径’)。具体的定义如下所示。

定义5:给定一个决策系统DS,NB(xi)表示距离xi的样本从小到大排序的集合

(8)

(9)

定义6:给定一个决策系统DS,∀B∈AT,则样本xi的分布半径定义为

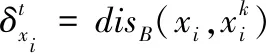
(10)

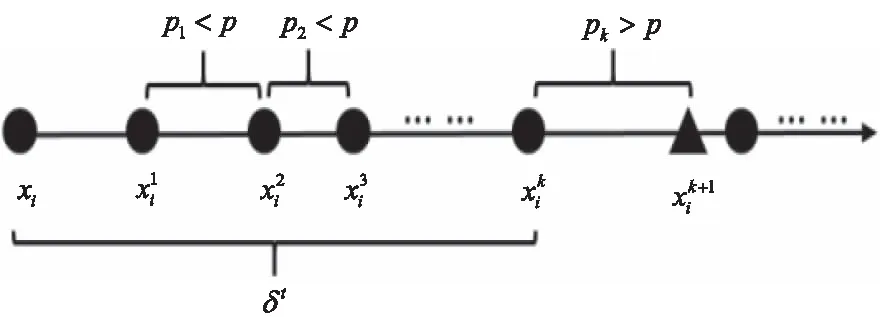
图1 分布半径选取图

图2 属性a1、a2下的样本图

相比于传统邻域粗糙集固定半径的粒化机制,分布半径可以针对每个样本的特点选择一个邻域半径,然而,仍不可避免出现粒化不精确的问题。如图2所示在属性a1、a2下样本的分布情况,假设这两个属性是约简后的最佳属性,然而观察在两类分界处的样本xi和yi,其邻域内仍包含不同类别的样本点,这可能会在属性评估时降低对这两个属性的分数,导致无法选出该属性。

针对这一问题,本研究对邻域半径进行缩减操作,减少邻域内异类样本,以期能提高这类样本的粒化精确度。考虑到不同属性与标签存在不同的关联度,最佳属性在一定程度上会与标签有更高的关联度,遂以此为思想来计算缩减比例,进一步提高粒化精确度。具体先计算每个属性与标签的关联度,然后根据关联程度决定邻域半径的缩减比例,具体定义如下。

定义7:给定一个决策系统DS,∀B∈AT,∀xi∈U,a(xi)表示样本xi在属性a下的取值,d(xi)表示样本xi在决策属性d下的取值,构建矩阵A如下所示

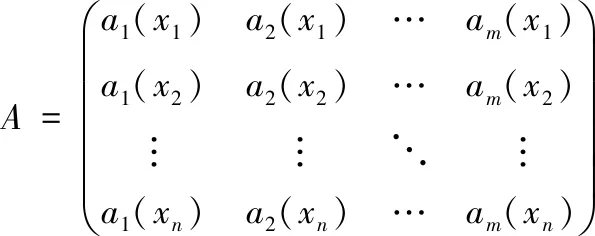
(11)

决策向量可表示为Y=(d(x1),d(x2),…,d(xn))T,条件属性与决策属性的相似度可以用向量表示为v=(v(a1),v(a2),…,v(an))T。则问题转换为

(12)

v=(ATA)-1ATY

(13)

|v(a)|表示v(a)的值,反应属性a与决策属性d的关联程度。|v(a)|的值越大,说明属性a与决策属性d的关联程度越大。接着为每个属性a计算关联度

(14)

其中ω(a)≥0并且∑ai∈ATω(ai)=|AT|。

定义8:给定一个决策系统DS,∀B∈AT,属性关联度向量表示为ω=(ω(a1),ω(a2),…,ω(am)),其中m表示特征的总数,则在条件属性B下,最终的动态邻域半径定义为

(15)

在实验中,设置0.1δt≤δD≤0.9δt,也就是说,若δD≤0.1δt,动态邻域半径为最小值δD=0.1δt,若δD≥0.9δt,动态邻域半径为最大值δD=0.9δt。

3.2 动态邻域关系及其粗糙集

定义9:给定一个决策系统DS,∀B∈AT,对于一个动态邻域半径δD,动态邻域关系可以定义为

DNB={(xi,xj)∈U×U：disB(xi,xj)≤δD}

(16)

根据邻域关系DN,容易得到样本xi的近邻为

DNB(xi)={xj∈U：(xi,xj)∈DNB}

(17)

定义10:给定一个决策系统DS,∀B∈AT,∀Xi∈U/IND(d),d关于B的动态邻域上下近似可以定义为

(18)

(19)

其中V、W∈U,是样本全集的子集。

定义11:给定一个决策系统DS,∀B∈AT,V∈U,在动态邻域关系下,d关于B的依赖度定义如下

(20)

3.3 属性约简

观察动态邻域粗糙集的上下近似发现,下近似并没有随着属性的增加而单调变化,这是因为邻域半径的动态变化,样本邻域中粒子个数并不随着属性的增加而具有单调性。为了方便设置属性约简的迭代停止条件,需要设计的属性约简策略让下近似具有单调性。通过研究样本淘汰(Sample Elimination)的约简策略,发现该方法在属性约简的过程中仅计算部分样本,若结合粗糙集理论,然后重新定义属性约简的过程中上下近似的定义,可以保证下近似的单调性,具体方法如下所示。

定义12:给定一个决策系统DS,B0=∅,并且Bi=Bi-1∪{a},a∈AT-Bi-1,i=1,2…,|AT|。V∈U,∀Xp∈U/IND(d)。属性集B的扩张模拟了属性约简的过程中属性的增加,上下近似计算公式定义为:

(21)

(22)

该策略保证了下近似的单调性,然而,观察算法发现这种迭代算法严重忽略了那些被淘汰的样本,被淘汰的样本可能在新属性加入时再次变的不确定,笔者称这类样本为不一致样本。在属性约简的过程中完全忽略那些淘汰样本的确定性变化会导致最终得到的约简属性集并不是一个最优的约简属性集。综上考虑,笔者提出了一个多准则的属性评估方法,把已确定的样本也纳入属性选择的考虑范围之内而不破坏下近似单调性的特点。具体定义如下所示。

(23)

其中|Q∩W|/|V|表示被淘汰样本中未变化的比例,也就是一致性样本的比例。其中当B=∅时,多准则属性评估函数退化为依赖度评估函数。公式(23)同时兼顾考虑了已被淘汰的样本,故称为一种多准则的属性评估。动态邻域粒化方式下的属性约简如算法1所示。

算法1:动态邻域粒化方式下的属性约简算法

输入:决策系统DS

输出:约简后属性集BR

1)初始化样本子集V=U,属性子集Sk=AT,约简后属性集BR=∅

2)计算每个属性a的关联度ω(a)

3)FOR each aiin Sk：

4)BR=BR∪{ai},Pai=∅

5) FOR each xiinV:

6)计算动态邻域半径δD

7)IF DNB(xi)中的样本是一致的:

8)Pai=Pai∪{xi}

9) End IF

10) End FOR

11)End FOR

12)选择属性ai满足ai=maxφai(d,V)

13)V=V-Pai,Sk=Sk-{a0},BR=BR∪{ai}

14)IF|Pai|/|V|≤θ：

15)输出BR

16) End

17)ELSE:

18)跳转至3)

其中θ是控制迭代算法停止的参数,实验设置θ=0.01。在算法中,首先计算每个属性的关联度,接着计算在每个属性下每个样本的动态邻域,判断邻域中的样本是否一致。最后使用提出的多准则评估函数选择满足条件的属性,直到算法停止。假设样本的个数为|U|,属性的个数为|AT|。上述算法中,需要对每个样本计算它的近邻且排序,时间复杂度为O(|AT|2*log|AT|)。每次迭代选择样本都要计算样本的一致性,所以算法的整体时间复杂度为O(|AT|2*log|AT|*|U|2)。

4 实验与结果分析

4.1 实验设置

为验证动态邻域属性约简(Dynamic Neighborhood Attribute Reduce,DNAR)算法的有效性,从UCI数据集中选取12个数据集,基本信息如表1所示。所有的实验均在Windows 10 PC, Intel(R)Core(TM)i5-6500 CPU 3.20 GHz,16G RAM,Python3.8实验平台进行。首先设置仿真实验验证动态邻域粒化机制的有效性,接着用本研究提出的邻域粗糙集属性约简算法与其他三个邻域粗糙集属性约简算法SNRS[9](SupervisedNeighborhood Rough Set)、NNRS[16](k-Nearest Neighborhood Rough Set)、NRS(δ-Neighborhood Rough Set)比较三个指标。第一个指标是约简后长度,第二个指标是分类精度,即被分类器正确分类的样本比例。第三个指标是Kappa系数,评价分类效果时平衡了随机分类对分类结果的影响。实验中参数采取对应研究中使用的数值,其中NRS算法中的邻域半径设置为δ=0.1,0.2,…,1,取在所有邻域半径下表现的均值。

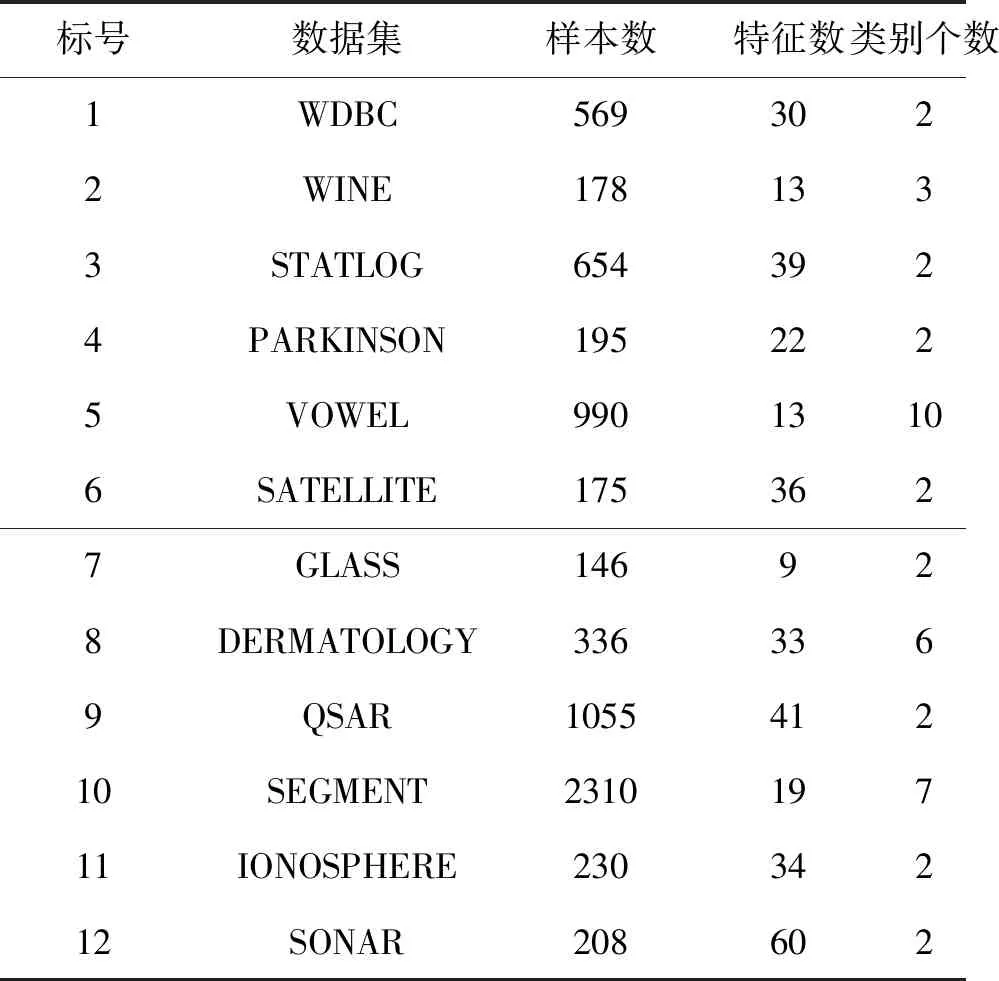
表1 UCI数据集的描述

实验采用了十折交叉验证的方法,即将原始数据集随机的等分为10个部分,其中挑选9组用于训练,1组用于测试,该过程会将重复10次,保证每一组都会作为训练数据和测试数据进行实验,以避免模型的拟合性问题的出现对实验结果产生偏差。另外在实验前均对所有数据集进行了标准化处理,以避免不同属性的取值差异过大对结果产生影响。

4.2 动态邻域粒化机制精确度分析

把12个UCI数据集按属性数量分成10个相等的子数据集,把第一个数据子集作为测试集1,前两个数据子集累加作为测试集2,以此类推得到10个测试子集,在10个测试子集上分别计算在分布邻域粒化机制下,和在其基础上缩减半径的动态邻域粒化机制下的邻域近似质量。在图3中,随着属性数量的逐渐增多,12个数据集的邻域近似质量并没有呈现出单调性变化,这是由于在两种粒化机制下邻域内样本随着属性增多是非单调的。通过观察图3发现,动态邻域较于缩减半径前的分布邻域相比有更高的粒化精确度,提高了信息粒化一致性的比率。

4.3 约简长度对比

表2展示了四种不同的方法在上述介绍的12个数据集上约简长度的比较,且是经过十折交叉验证得到结果的均值,约简长度越小,代表删除的属性越多。观察表2得出以下结论:DNAR算法在所有数据集上都能约简合适数量的属性,而其他三个算法在部分数据集上约简后属性数量过多过少,这反应了DNAR算法能够处理不同类型的数据集。例如,SNRS算法在5个数据集上约简后的平均属性个数都为1,NNRS算法在QSAR数据集上几乎无法约简,这说明对比算法依靠固定的邻域半径不能处理这些数据集。约简长度对比实验说明DNAR算法能处理不同分布的数据集且约简合适的属性长度。在3.3节的分类精度对比也证明了DNAR算法约简后属性的质量比其他算法约简后的属性质量要高。

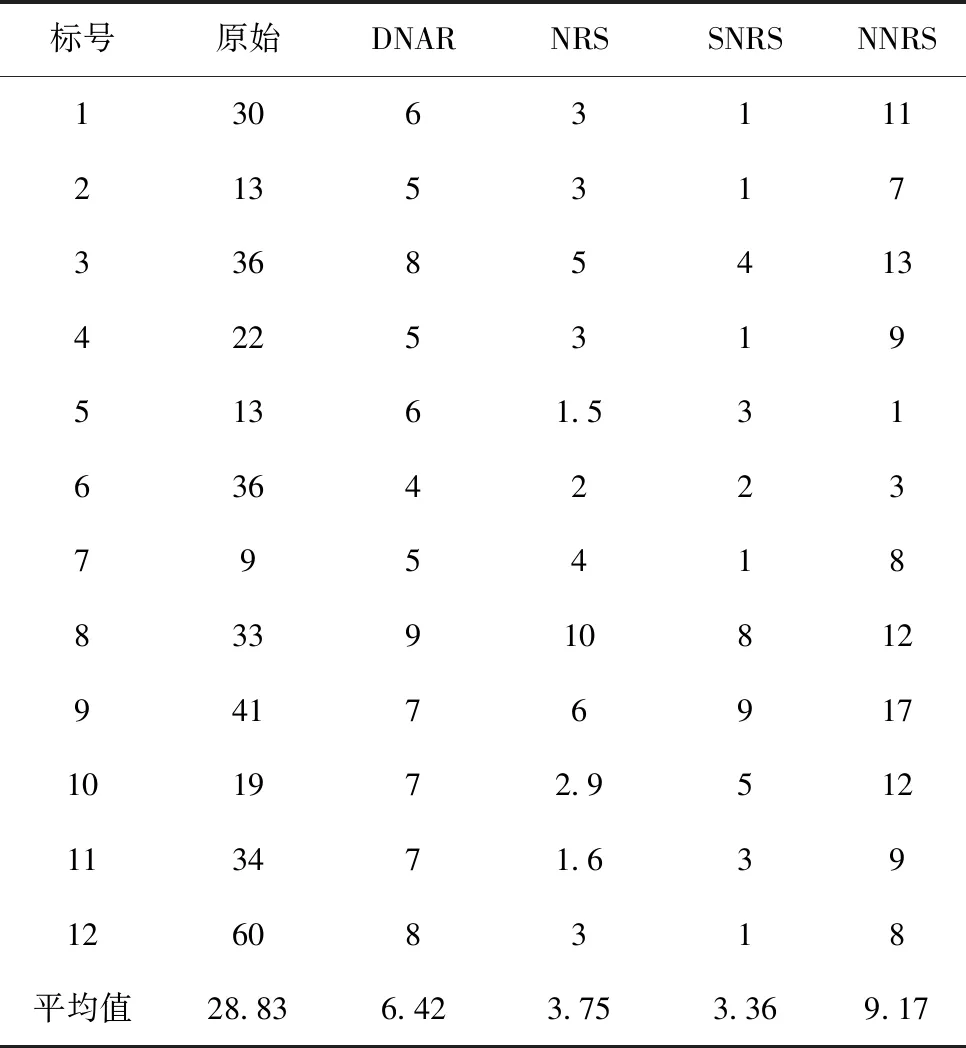
表2 约简长度的对比

4.4 分类准确率对比

在本组实验中,采用KNN分类器和SVM分类器,利用属性约简后的结果对测试数据集进行分类,并且计算分类准确率,最后求出分类准确率的平均值和最大值。分类准确率结果如表3和表4所示,在每个数据集上的效果最好的算法得出的准确率用粗体标出。从表3和表4中可以看出,无论是采用KNN分类器还是SVM分类器,利用DNAR算法所求得的约简,其对应的平均分类准确率,在多数数据集上都优于其他算法。结合3.2节的结果表明,DNAR算法能够有效的删除冗余属性且保留最佳的属性。

表3 在KNN分类器上分类精度的对比

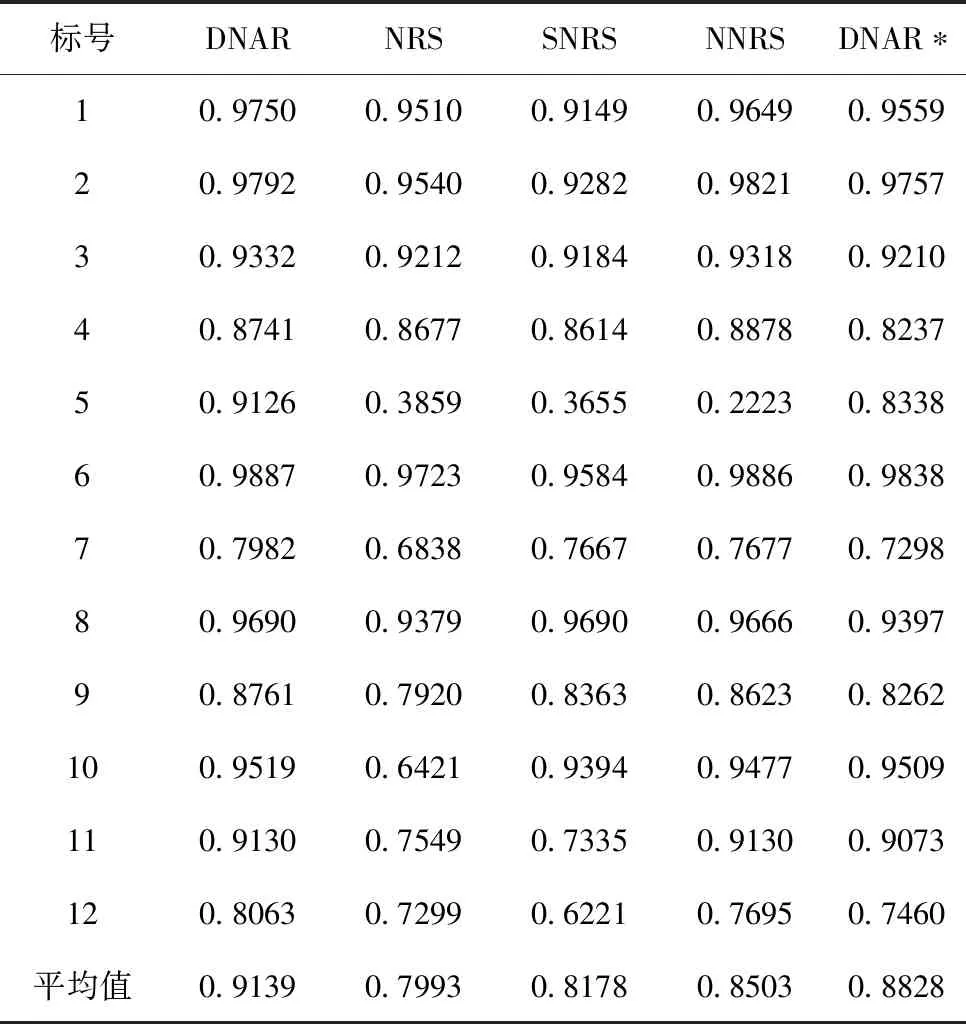
表4 在SVM分类器上分类精度的对比

为了验证2.3中提出的多准则属性评估方法的有效性,设计了一种在DNAR下未使用多准则属性评估而使用近似质量评估属性的算法DNAR*。实验结果表明,加入多准则属性评估的DNAR算法在12个数据集下,分类准确率都要高于DNAR*。注意到在SONAR数据集上,DNAR算法比DNAR*算法准确率提高8%左右。这说明了本研究提出的多准则属性评估方法能有效的减少不一致的样本。

4.5 Kappa值对比

为了进一步了解DNAR算法的性能,在本小节中利用Kappa统计在KNN分类器和SVM分类器下进行分析。Kappa的数值在-1到1之间,数值越大,说明预测的结果越理想,反之说明预测的结果不理想。实验结果如表5,表6所示,最优值用粗体标出。

表5 在KNN分类器上Kappa值的对比

根据表5,表6中的实验结果显示,在KNN分类器下,其中10个数据集上都优于其他算法,且在11个数据集上的值都高于0.8。在SVM分类器下,在10个数据集上都优于其他算法,且也在11个数据集上的值高于0.8。总体来看,DNAR算法的Kappa系数平均取值也优于其他算法。

5 结语

在邻域粗糙集的背景下,针对已有的邻域关系采取固定邻域半径粒化策略导致粒化不精确的问题,提出一个动态邻域粒化的策略,并且定义了动态邻域关系,构建相应的粗糙集模型。与此同时,针对下近似单调性问题,通过融合动态邻域至样本淘汰的属性约简算法中得以解决,并改进了其属性评估方法。实验结果表明,相较于传统邻域关系和其他新型的邻域关系,采用动态邻域关系,计算约简结果,可在不同数据集上都获得一个较优的约简结果,并且所得到的约简在分类准确率上也优于对比算法。