基于可拓展机器学习的失真图像视觉复原仿真

2023-09-20孙国娇李长硕

计算机仿真 2023年8期

孙国娇,李长硕

(1. 吉林建筑科技学院艺术设计学院,吉林长春 130000;2. 长春大学,吉林长春 130000)

1 引言

图像在传递与转换过程中有较大概率造成图像质量下降[1,2],也就是图像产生失真问题。图像的清晰度对于图像对于应用具有重要意义[3],因此失真图像复原问题的研究十分必要。

以往普遍使用的失真图像复原方法多以头脑风暴优化算法或深度强化学习算法为核心[4,5],前者通过头脑风暴优化算法处理多峰高维函数问题,获取BP神经网络初始权值与阈值,提升收敛速度并降低误差,实现失真图像复原。后者将强化学习算法与对抗网络相结合,实现失真图像复原。但上述方法在实际应用过程中需设定正约束条件,或者图像的复原过程需符合广义平稳过程假设,导致上述算法运行过程中需进行海量计算,导致实际应用价值受到约束。针对这一问题,研究基于可拓展机器学习的失真图像视觉复原方法,通过研究机器学习算法的可拓展性,提升机器学习算法的处理效率,实现高效、高质的失真图像视觉复原。

2 基于可拓展机器学习的失真图像视觉复原方法

2.1 基于最小二乘支持向量机的失真图像复原

以s(x,y)表示物体u(x,y)经过光学系统获取的图像,利用式(1)描述s(x,y)失真模型:

s(x,y)=n(x,y)×δ+u(x,y)d(x,y)

(1)

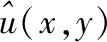
采用最小二乘支持向量机对s(x,y)进行复原,在此过程中选取大量的s(x,y)与初始图像u(x,y)样本实施学习训练,将s(x,y)和u(x,y)分别作为用于失真图像复原的回归模型的输入与目标输出,由此构建两者间的非线性映射关系f(·)

u(x,y)=f(s(x,y)×φ)

(2)

式(2)内,φ表示映射系数。

基于非线性映射关系构建用于失真图像复原的回归模型,通过训练后的回归模型复原s(x,y)。f(·)的构建无需获取图像失真的详细模型,仅仅由学习训练即可实现。值得关注的一点内容为:用于学习训练的s(x,y)与待复原的s(x,y)是在同一状态下获取的[6],也就是两者的d(x,y)和n(x,y)一致。

在构建f(·)时选取邻域对像素方法[7],定义用于失真图像复原的回归模型中u(x,y)内各像素值仅受s(x,y)相应邻域像素值影响。以256×256像素的图像进行说明,以3×3像素的邻域对s(x,y)依行或列的顺序逐点滑动,获取(256-3+1)2=2542=64516个邻域,同时将这些邻域中心作为采样点对u(x,y)实施采样处理,由此获取64156个像素值,也就是对s(x,y)和u(x,y)构建64156个3×3像素对1个像素的映射。依照行或列的顺序配列邻域像素产生9维输入对1维输出的非线性映射,训练数据对为64156。

上述构建f(·)的方法不仅与图像失真的物理过程更加匹配,且在邻域大小为3×3像素的条件下,该方法组建的输出节点显著降低,而训练数据对数大幅提升,也就是利用较多的训练数据训练简单的非线性映射,由此可提升映射性能。

在失真图像复原过程中,利用机器学习算法中的最小二乘支持向量机构建64156个9维输入对1维输出。最小二乘支持向量机就是在支持向量机理论中引入最小二乘原理,构建一个可令间隔达到上限的超平面,令不同类别内距分类线最近的样本间距离达到上限[8,9]。最小二乘支持向量机对各数据点均添加一个令不等式约束转换为等式约束的修正值zi,因此仅计算线性等式方程组即可,由此降低计算量,并无需进行支持向量机内选取惩罚因子的过程。

失真图像复原过程中,对最小二乘支持向量机优化超平面的计算就是对式(3)所示的凸优化问题进行计算

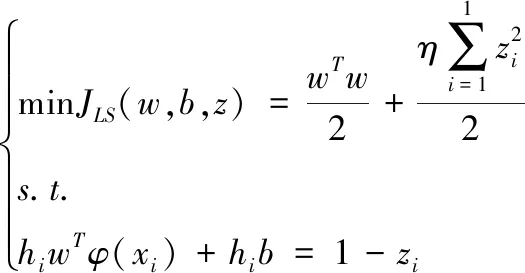
(3)

式(3)内,(w,b)和η分别表示超平面和可调参数。φ(xi)表示第i个样本的输入模式,hi表示类别标签。

利用式(4)描述Lagrange函数:

(4)

式(4)内,ci表示Lagrange乘子。依照KKT条件:忽略不需要计算的w和b,并进行展开处理,得到线性方程组

(5)

将式(6)带入KKT条件内并进行分析能够得到,失真图像复原过程中,样本点的数量对矩阵方程的系数矩阵产生直接影响[11]。由此能够获取最小二乘支持向量机分类器:

h(x)=sign(∑cihiK(x,xi))+sign(b)

(6)

式(6)内,K(·)表示核函数。

2.2 并行化失真图像视觉复原

通过基于映射—规约模型的最小二乘支持向量机可拓展架构,实现并行化失真图像视觉复原,解决失真图像视觉复原的可扩展性。作为一种并行计算模型,利用映射—规约模型可处理基于机器学习中,最小二乘支持向量机的失真图像复原并行化问题及拓展性问题等。此模型通过映射与规约的处理过程体现相关算法[12]。映射处理过程中,基于各输入失真图像能够生成一个对应的输出初始图像,直接完成失真图像复原过程的并行处理;规约处理过程需统计全部输入元素获取输出结果,同时失真图像复原的并行处理过程中选规约处理不同数据块,在此基础上整合不同数据块的结果。通过映射—规约模型描述失真图像复原过程中所使用的最小二乘支持向量机算法,能够自然地获取算法的并行性,将映射至并行架构内。

基于最小二乘支持向量机算法的失真图像复原训练过程采用SMO训练算法[13],训练过程集中在更新修正值zi和参数η与ci,同时在图像样本数量提升的条件下,这两部分的更新运算所占比重越高。为提升失真图像复原的运算效率需对上述两部分更新过程实施并行化处理。利用映射—规约模型描述上述两部分更新过程,通过各训练样本独立更新zi,对映射处理相对应;通过对比整个zi数组内的元素更新参数η与ci,这与规约处理相对应。

针对失真图像复原过程中所使用的最小二乘支持向量机,分析式(6)能够发现核函数与系数相乘的运算针对各支持向量独立实施,与映射处理相对应,相对之下最小二乘支持向量机的求和过程与规约处理相对应。由此最小二乘支持向量机分类过程同样可通过映射—规约模型而完成并行处理。

基于上述分析能够得到采用映射—规约模型能够实现最小二乘支持向量机分类器的可拓展硬件架构,如图1所示。

图1 最小二乘支持向量机分类器的可拓展硬件架构

图1所示的整体结构由一个主控模块和若干个执行映射与规约处理的并行失真图像复原处理模块,各模块间利用具有广播功能的总线结构进行连接[14]。总线上仅存在主设备—主控模块,因此其结构较为简单,易于拓展。硬件的整体运行分为设备配置环节、数据加载环节、训练环节和分类环节等。

主控模块的主要功能为控制失真图像复原过程中最小二乘支持向量机的训练过程,同时发送数据、整合结果与除映射与规约外的剩余运算过程。其中的内存单元能够存储用于训练的64156个失真图像9维输入与Lagrange乘数数组。并行失真图像复原处理模块的主要功能为完成映射与规约处理,在训练环节中若干个并行失真图像复原处理模块共同实现更新值与参数的更新。以最大限度利用数据的局部性防止循环传输数据导致的性能下降,各并行失真图像复原处理模块均在本地存储部分失真图像9维输入样本和与之相对的修正值和相关数组。

训练环节中,进行映射处理前主控模块向不同并行失真图像复原处理模块同时写入对应的图像样本数据与相关信息,并在不同并行失真图像复原处理模块内的输入向量更新修正值[15]。在完成规约处理过程中,不同并行失真图像复原处理模块依照本模块内的修正值与图像相关数据确定各参数中间值,在此基础上主控模块统计不同并行失真图像复原处理模块的结果确定各参数最终结果,并确定是否需要继续更新。

分类环节中,主控模块将图像相关数据传输至各并行失真图像复原处理模块内,在此基础上实施映射与规约处理进行式(6)的运算。主控模块统计各并行失真图像复原处理模块的结果实现失真样本复原过程中最小二乘支持向量机构建64156个9维输入对1维输出,完整输出分类。

3 仿真结果与分析

实验为验证本文所研究的基于可拓展机器学习的失真图像视觉复原方法在实际失真图像复原过程中的应用效果,以某实验室图像数据库为实验对象,该实验对象内包含人像、动物图像和建筑图像三个数据集。针对该实验对象,在FPGA平台中采用本文方法进行仿真测试,所得结果如下。

3.1 主观图像视觉复原结果

在实验对象的三个数据集内分别随机选取一幅图像进行图像视觉复原测试。所选三幅图像的像素均为256×256像素,以方差为3的高斯函数在频域上对所选三幅图像进行失真处理,所得失真图像如图2所示。采用本文方法对三幅失真图像进行视觉复原处理,所得结果如图3所示。

图2 失真图像

图3 本文方法复原图像

分析图2和图3能够得到,在视觉传达效果上,采用本文方法对失真图像进行复原能够显著提升失真图像的清晰度,由此说明采用本文方法对失真图像进行复原是有效的,这是由于本文方法利用最小二乘支持向量机的非线性映射能力构建失真图像与初始图像间的映射关系,由此实现失真图像视觉复原。

3.2 基于视觉传达均方误差的图像失真复原性能判断

参考均方误差与峰值信噪比的定义,结合视觉传达函数,通过二范数计算视觉传达均方误差,以此实现图像失真复原测量。视觉传达均方误差与均方误差相比,主要区别为前者内结合了视觉传达函数,通过视觉传达函数能够体现人眼视觉感知特征对于图像质量分析的影响。通过计算视觉传达均方误差能够客观准确地测量复原后图像质量。

视觉传达函数所描述的是基于人类视觉模型的测量函数。考虑人眼视觉系统的复杂性,当前尚未研究出较为准确的视觉传达函数表达式。根据人眼视觉系统理论框架能够得到人眼视觉系统中模拟了与图像质量相关的视觉传达三大特性:幅度非线性衰减、视觉敏感度带通与视觉检测,由此能够证明视觉传达函数能够描述二维随机域上的视觉传达三大特性。考虑视觉心理生理学的影响,在视觉传达函数的描述种需添加心理生理学函数,其主要功能为计算视觉传达函数时调节部分参数与阈值。将视觉传达函数转换为与图像质量相关的视觉传达三大特性函数,由此提升视觉传达均方误差计算过程中视觉传达函数的应用性。

视觉传达均方误差的取值范围为[0,5],其取值越小说明复原后的图像视觉传达效果越接近原始图像。

基于图2的真实图像和图3本文方法的复原结果,利用视觉传达均方误差判断本文方法图像失真复原性能,所得结果如图4所示。同时为进一步说明本文方法的视觉复原性能,以文献[4]中基于头脑风暴优化算法的方法和文献[5]中基于深度强化学习的方法为对比方法,分析两种对比方法的图像复原结果,所得结果如图4所示。