改进蚁群算法在移动机器人路径规划中的应用

杨树广,董西松

(1 山东交通学院轨道交通学院 山东 济南 250000) (2 中国科学院自动化研究所多模态人工智能系统全国重点实验室 北京 100190)

0 引言

伴随着工业的快速发展,工业设备广泛应用于制造业、建筑业、物流、矿山开采等领域,在各种应用场景中朝着自动化、智能化等方面发展。智能工业设备可以看作一种能自动控制、可重复编程、多功能、高度灵活的多功能机器人,它具备一些与人大脑相似的思考行为,例如:依靠传感设备的感知能力、复杂环境下的路径规划能力、不同动作的协调能力和其他设备的协同能力等。移动机器人的路径规划是指机器人在其工作空间自行规划出最优或者较优的安全路径[1]。目前常被人们使用的路径规划方法有很多种,例如遗传算法、人工势场法、粒子群算法、Dijkstra算法、蚁群算法等,每种算法都有自己的优缺点。在研究经典算法的过程中,发现蚁群算法的鲁棒性强、每次搜索相对独立、有正反馈等特点,但是在复杂环境下也存在寻找最优路径能力较差和容易陷入局部最优等问题。

针对蚁群算法的缺点和问题,很多学者进行了大量的研究。LUO Q等[2]构造了不平等分配初始信息素,采用伪随机状态转移规则进行路径选择,自适应调整确定选择和随机选择的比例,提高了算法的全局最优搜索能力和收敛速度;陈丹凤等[3]提出一种基于强化学习和人工势场改进的蚁群算法,利用强化学习对蚁群算法的参数进行配置,引入人工势场算法的局部优化机制,提升算法避障能力,实现更快更平稳的路径规划效果;刘海鹏等[4]采用一种奖惩机制对路径上的信息素进行更新,还利用拐点优化算法与分段B样条曲线相结合的方法来进行路径优化,有效地改善了路径的平滑性;周敬东等[5]通过改变初始化信息素浓度分配、改变启发式函数、采取蚂蚁回退策略、引入蚂蚁优化排序等方法对蚁群算法进行优化,提高了算法的鲁棒性和寻优能力;钱平等[6]提出了蚁群算法本身参数及融合遗传算法以及加入平滑机制,提高了路径水下机器人路径规划的整体性能。

受到上述研究的启发,针对经典蚁群算法一般容易陷入局部最优和容易出现停滞现象等不足,本文采用以下改进策略。

(1)将当前步长和终点欧氏距离结合起来的方法改进启发函数,并且引用了前位置因子ε和终点位置因子μ,搜索路径的方向性得到了加强。

(2)将信息素挥发程度改为一个动态的更新方式,使算法拥有了较好的收敛性。在与经典蚁群算法比较中得出,改进蚁群算法增大了蚂蚁选择最优路径的可能性,避免出现局部最优解,提高了算法收敛速度的同时,具有较好的全局搜索能力,使原有算法的各项指标都得到提升。

1 移动机器人的环境模型

构建环境地图的目的在于帮助移动机器人在建立好的含有障碍的环境模型中规划出一条从起点到目标点的最优路径。建立适用于移动设备路径规划的环境模型已经有了许多成熟的方法,现有的基本的环境模型主要包括栅格分解图、四叉分解图、可视图、Voronoi图。其中栅格分解图的代表性强,构建方法较为简单和后期维护成本低。栅格分解图就是假设移动机器人的工作环境是在一个二维空间,将空间按照单位大小的正方形划分为大小相同的单元。一般情况下,在栅格分解图建模中,0表示可以自由移动的区域,1表示的是存在障碍物的区域,0和1分别对应了白色和黑色区域。本文不考虑障碍物的形状,如果障碍物所占面积不足一个栅格面积时,也按照一个栅格的面积进行计算。

移动机器人的环境地图建模如图1所示,栅格分解图中的x、y坐标轴和一般的坐标轴递增顺序是一样的。栅格分解图共有i行m列,单个栅格边长为1,则每个栅格中心坐标可以表示为式(1)所示:

图1 移动机器人环境模型

(1)

式(1)中xi、yi表示此点中心位置的横坐标、纵坐标;mod(*)表示除后的余数;ceil(*)表示每个元素四舍五入到大于或等于此元素的最接近的数。

2 经典蚁群算法

2.1 算法基本原理

我们所熟知的蚂蚁在大自然中寻找食物时,会留下类似于信息素之类的物质,其他蚂蚁可能感知到先前蚂蚁留下的这种物质。我们用信息素浓度的表征此路径的长短,所以在较短的路径上的信息素浓度较高。信息素的浓度也会影响蚂蚁选择路径的概率,再加上蚁群在路程中也会留下信息素,最终会形成一个正反馈,不断引导着蚁群寻找出最短的路径。

2.2 算法公式

(2)

ηij=1/dij

(3)

式(2)中,τij(t)表示t时刻i到j上的信息素浓度;ηij(t)为启发函数,表示蚂蚁从i到j的期望程度;allow表示属于可以行进的地图点;α表示信息素重要因子;β表示启发函数重要因子。

在蚁群经过某个路径会留下信息素的同时,原有的信息素浓度也会慢慢下降,设定参数ρ(0<ρ<1)表示信息素的挥发程度。所以,当循环一次后,已经走过的每个路径上的信息素浓度会产生变化,其公式如式(4)所示:

(4)

3 蚁群算法的改进

3.1 改进启发函数

蚁群算法中的启发函数只是将下个节点与终点之间的欧氏距离考虑进去,考虑的因素太单一,容易陷入局部最优解。如果在原有公式加入当前位置到下个选择可选择位置的欧氏距离,路径的搜索的方向性被增强。在计算中加入位置因子可以调整两个距离的权重,这样能使算法的调整变得灵活。其公式如式(5)所示:

(5)

式(5)中,dis表示从当前节点和下一个待选节点之间的欧式距离;djE从下一个待选节点到E终点的距离的欧式距离;ε表示当前位置因子;μ表示终点位置因子。

3.2 改进信息素挥发程度

蚁群算法中的蚂蚁是依靠信息素来做去强化最优路径的选择,随着时间额推移,以前留下的信息素会逐渐消失。信息素的挥发程度会直接影响算法收敛快慢和对全局路径的搜索,它表示了蚂蚁群中的每个蚂蚁之间会相互影响路径的选择,是蚂蚁获取外界信息的途径。将信息素挥发程度改为一个动态的更新方式会让蚁群搜索更多的可行路径,随着迭代次数的增加ρ逐渐减小,蚂蚁将朝着信息素浓度增高的路径集中,因此会增快收敛速度。其公式如式(6)所示:

(6)

式(6)中,T代表总迭代次数;t代表当前迭代次数。

4 仿真实验验证及分析

为了验证改进蚁群算法加快了收敛速度的同时具有较高的全局搜索能力等方面的优化效果,在MTALAB2022a上选用20×20规模和30×30规模的栅格分解图对于改进后的蚁群算法进行仿真。实验运行电脑的操作系统为Windows10,处理器为Intel i7-7700HQ CPU,内存为16 GB,起始点和终点分别设置在栅格分解图的左上方与右下方。算法基本参数:迭代次数K=100次;蚂蚁的数量M=50只;信息素重要程度因子α=1.2;起点位置因子ε=0.4;终点位置因子μ=0.6;启发函数重要因子β=8;信息素的挥发程度ρ=0.6。

4.1 20×20栅格分解图仿真

基于表所给的参数指标,首先使用20×20的固定障碍物的栅格分解图分别对经典蚁群算法和改进蚁群算法进行仿真实验,结果如图2、图3所示,并对结果进行对比。

图2 20×20经典蚁群算法收敛曲线变化趋势和运动轨迹图

图3 20×20改进蚁群算法收敛曲线变化趋势和运动轨迹图

从本次仿真结果得出改进蚁群算法的最优路径长度和迭代次数为31.799 m和15次,比经典蚁群算法的路径长度减少了10.58%,迭代次数减少了51.61%。仿真结果表明,改进蚁群算法的收敛速度远高于经典蚁群算法,同时容易看出其各项指标更加优越。

4.2 30×30栅格分解图仿真

为进一步验证本文算法的优越性,在30×30的固定障碍物的栅格分解图中将两种算法再次进行对比仿真实验,各个参数设置和4.1中保持一致。结果如图4、图5所示,并对结果进行分析。

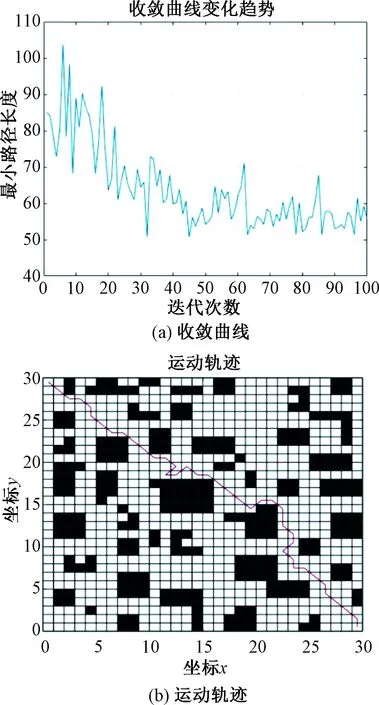
图4 30×30经典蚁群算法收敛曲线变化趋势和运动轨迹图

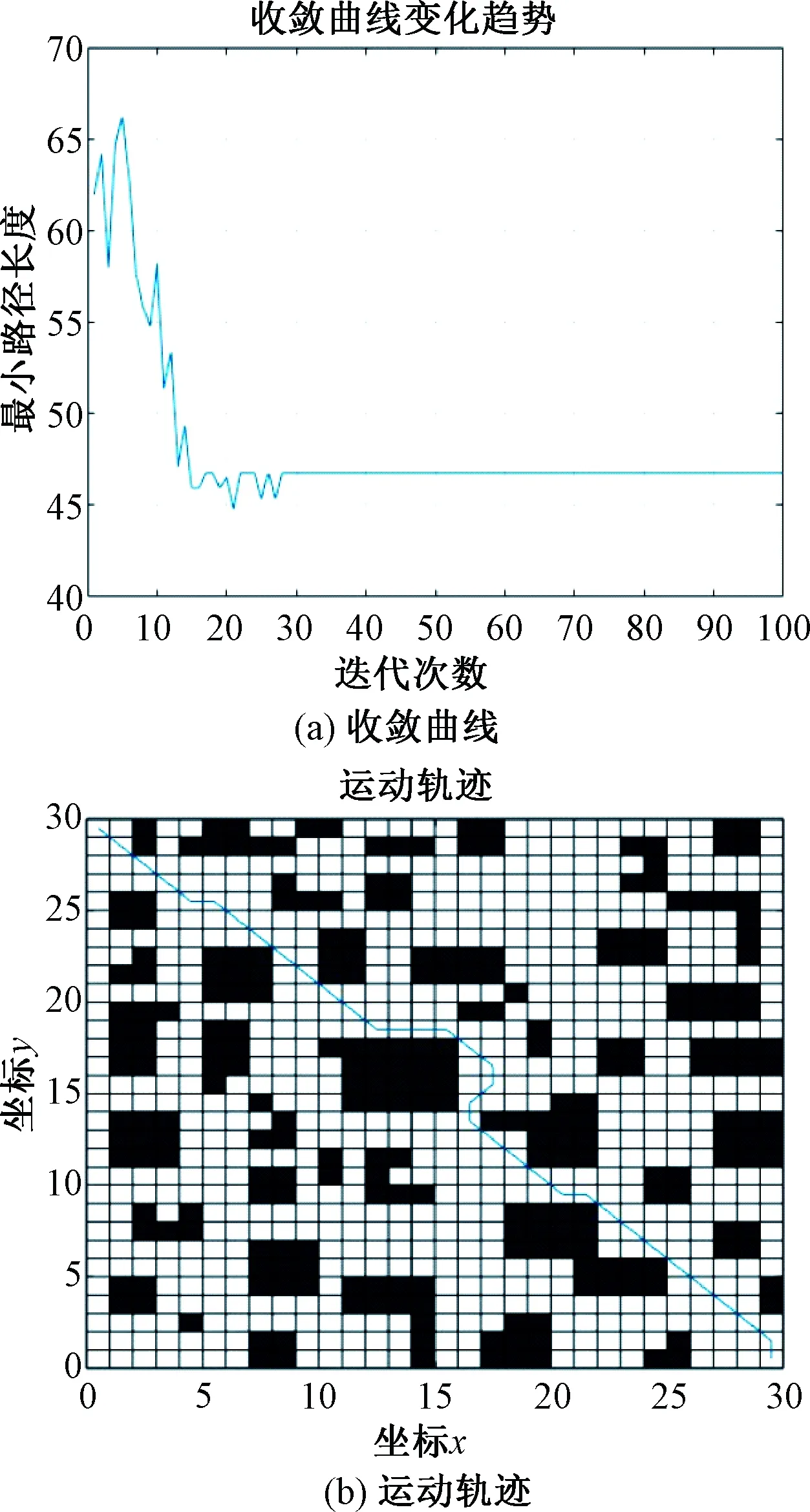
图5 30×30改进蚁群算法收敛曲线变化趋势和运动轨迹图

从本次仿真结果来看经典蚁群算法前期路径搜索方向较差,容易陷入局部最优和选择方向错误,这是因为信息素的挥发程度在迭代开始时分布均匀,信息素的挥发程度的正反馈不强,启发式信息的方向变弱。经典蚁群算法在30×30的仿真实验中稳定性很差,直到最后也没有能迭代收敛,甚至在搜寻路径的过程中还出现了方向的混乱。改进蚁群算法在第28次迭代时就能够收敛,此时的路径长度仅为46.769 6 m,并且没有出现方向混乱。

5 结语

综上所述,本文通过两组对比实验在20×20和30×30的栅格分解图中路径规划的最优路径长度、找到最优路径的迭代次数等数据,说明了改进蚁群算法能有效减少最优路径的迭代次数,加快收敛速度,增加规划轨迹的平滑度等方面均优于蚁群算法,此外经典蚁群算法在处理较为复杂的地图时会出现各种问题,证明本次算法在路径规划问题求解上的实用性。移动机器人属于大型设备,对于路径的平滑程度、稳定性和迭代次数都有较高的要求。改进蚁群算法能满足设备运行的同时也提高了设备的安全性,使用户的使用变得更加高效便捷。