基于颗粒阻塞变刚度驱动器的折纸单元设计

杜静恩，许勇，贾云博，刘凌霄，高美妍

（1.201620 上海市 上海工程技术大学 机械与汽车工程学院；2.201620 上海市 上海工程技术大学 航空运输学院）

0 引言

折纸单元是由二维的纸通过弯曲折叠形成的具有一定功能价值的三维结构，由于其较好的空间可折展性受到了广泛关注。目前折纸原理广泛应用于机械超材料[1-3]、自折叠机器人[4]、食品包装[5]、医疗器械[6]等领域，越来越多的学者研究折纸单元独特的力学性能及其应用场景。Liu 等[7]将折纸单元制成能灵活变换位姿的柔性臂；Waitukaitis 等[8]利用三浦折纸自锁引发的强化效应设计出刚度可编程的机械超材料；Feng 等[9]发现水弹折纸管可以通过非刚性扭转实现变刚度。但是包括折纸单元在内的柔性单元大都存在刚度不足的情况，学界一直都在积极寻找变刚度方案。Amend 等[10]在设计的柔性抓手中加入了固体颗粒，大大加强了负压状态下柔性抓手在抓取与放置重物时的刚度与准确性；Jiang 等[11]制作了基于颗粒阻塞变刚度原理的气动执行器；Zhao 等[12]研究了填充颗粒的空间占用率对颗粒阻塞变刚度的影响。

本文将刚性折纸原理与颗粒阻塞变刚度的原理结合，设计了基于颗粒阻塞原理的变刚度折纸单元，建立了折纸单元的数学模型。

1 基于颗粒阻塞原理的变刚度折纸单元设计

基于颗粒阻塞原理的变刚度折纸单元如图1 所示，由折纸单元和多个变刚度驱动器组成。变刚度驱动器贴合在折纸单元的折痕处，柔性状态时随折痕一起变化，刚性状态时会阻碍折痕弯折。

图1 变刚度折纸单元三维效果Fig.1 3D effect display of variable stiffness origami unit

如图2 所示，图2（a）为由折纸启发的折纸单元的立体结构，折纸单元的上下两平台由折叠单元连接。图2（b）为折纸单元平面展开图，其中实线为山折痕，虚线为谷折痕。

图2 折纸单元三维结构及平面折痕Fig.2 Three-dimensional structure and plane crease of origami unit

基于颗粒阻塞原理设计了变刚度驱动器，如图3 所示。变刚度驱动器由密封袋、颗粒阻塞囊和气孔组成，气孔外接真空泵可改变密封袋内气压，单个颗粒阻塞囊由矩形透气袋和袋内填充颗粒组成。

图3 基于颗粒阻塞原理的变刚度驱动器结构Fig.3 Variable stiffness actuator structure based on particle blocking principle

以主动折痕G2O2处为例，变刚度驱动器对称固定在主动折痕两侧，效果如图4 所示。其余所有主动折痕处的固定方法一致。

图4 折纸单元的主动折痕处的变刚度驱动器Fig.4 Variable stiffness driver at active crease of origami unit

2 颗粒阻塞变刚度驱动器刚度分析

变刚度驱动器的刚度k的计算公式为

为获得颗粒阻塞囊刚度，需分析颗粒阻塞囊的弯曲变形。本文遵循平面内常曲率弯曲假设，如图5 所示，c为弯曲弧段中心O到弯曲轴线的距离，即弯曲部分曲率半径。矩形横截面长、宽为d、L。

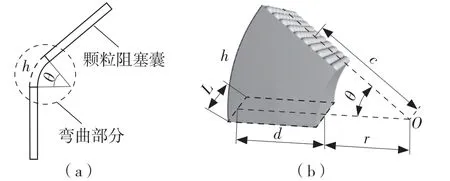
图5 未受载时颗粒阻塞囊高刚度状态弯曲变形模型Fig.5 Bending deformation model of particle blockage capsule under high stiffness without load

密封袋内压强为Pb、袋外压强为Pa，内外压强差为Pa-Pb，在此压强差作用下密封袋会将松散的颗粒挤压成致密的刚体颗粒团，且随着内外压强差的增大，整个驱动器的刚度也增大。当颗粒阻塞囊受到载荷F时，其弯曲角度由未受载时的θ增大至θ+δ，如图6 所示。

图6 受载时颗粒阻塞囊高刚度状态弯曲变形模型Fig.6 Bending deformation model of particle blockage capsule under high stiffness loading

抽真空后颗粒阻塞囊为高刚度状态，填充颗粒在颗粒阻塞囊内的空间占用率定义为

式中：——颗粒阻塞囊中所有填充颗粒的体积总和，由颗粒阻塞囊中填充颗粒的数量N和填充颗粒的半径r决定，其值为

式中：Vc——变刚度驱动器的密封袋容积，由变刚度驱动器最大体积Vmax真空泵抽气速率S和抽气时间t决定，关系式为

且存在边界条件：Vc≥V0，其中V0为颗粒阻塞囊弯曲部分处于立方体状态下占用的空间，其值为

变刚度驱动器为刚性状态且颗粒阻塞囊弯曲角为θ时，填充颗粒在颗粒阻塞囊内的空间占用率Δ1为

颗粒阻塞囊在刚度变化后，在不受外力情况下空间占用率为定值，故弯曲角为θ时弯曲部分占用的空间V1=V2。受到外力F的作用，曲率中心由O转移到O'，此时变刚度驱动器中颗粒在高刚度状态下占用的空间V2为

式中：C'——弯曲中心到矩形横截面形心的距离；γ——中心角；——带增量角的弯曲角，即

此状态下的空间占用率Δ2为

颗粒阻塞囊体积与填充颗粒的空间占用率间有如下关系

此时弯曲角增量与填充颗粒的空间占用率的关系为

颗粒阻塞囊在刚性状态下承受外力时，颗粒与透气袋间摩擦力产生的曲率中心所在的轴的摩擦力矩为Mf。由流体加压模型可知，变刚度驱动器内外壁各部分受到的压力是相等的。施加外力后颗粒阻塞囊会发生一定的变形，因此颗粒阻塞囊内的压强会变大，根据两圆球赫兹接触模型可知，颗粒间的等效压力为

由图7 可知，颗粒阻塞囊与透气袋间的摩擦力提供的锁紧力关于轴线SS'对称，且总的锁紧力为

图7 变刚度驱动器内静态力f1 及锁紧力矩Mf 方向Fig.7 Direction of static force f1 and locking torque Mf in variable stiffness driver

锁紧区域A1上的静态力f1由颗粒与透气袋间的正压力P'决定，故单个颗粒阻塞囊由锁紧力Ff提供的锁紧力矩为

颗粒阻塞囊的刚度即为变刚度驱动器的刚度。

3 变刚度驱动器性能仿真

变刚度驱动器中颗粒阻塞囊的参数设置：弯曲部分的弯曲中心到矩形横截面形心距离C=5 mm，矩形横截面的长L=20 mm，宽d=5 mm，总高H=20 mm，弯曲部分的曲率半径R=2.5 mm，弯曲部分外侧最大长度h=5 mm，填充颗粒半径r=0.5 mm，材质为ABS，弯曲部分能装满该尺寸的颗粒数N=3 819，真空泵抽气速率S=50 mm3/s，变刚度驱动器内压强Pb=0.02 MPa，变刚度驱动器外压强Pa=0.101 MPa。

通过MATLAB 按式（2）—式（5）计算空间占用率，结果如图8 所示。由图8（a）可知，随着真空泵对变刚度驱动器内部抽气，颗粒的空间占用率会逐渐提高，最大占用率约为72%。由图8（b）可知，变刚度驱动器内部压强越小空间占用率越高。

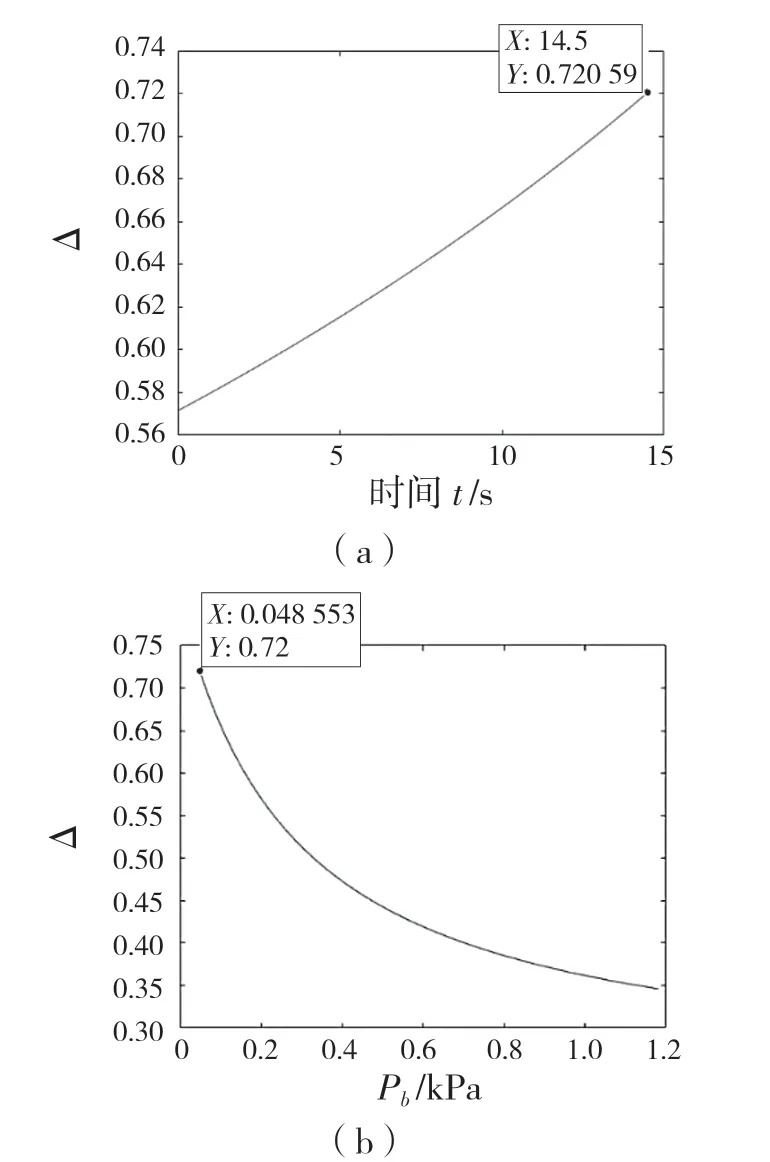
图8 填充颗粒空间占用率Δ 随t 和Pb 的变化Fig.8 Change of space occupancy of filled particles Δ with t and Pb

由式（12）、式（15）可知，变刚度驱动器内压强Pb与颗粒阻塞囊内填充颗粒半径都是影响最终锁紧力矩的因素。由图9 可知，变刚度驱动器内压强越大颗粒阻塞囊的锁紧力矩越小。颗粒阻塞囊的锁紧力矩随着填充颗粒半径的增大而减小，如图10 所示。

图9 颗粒阻塞囊内压强与锁紧力矩的关系Fig.9 Relationship between pressure and locking torque in particle blocking capsule

图10 填充颗粒半径与锁紧力矩的关系Fig.10 Relationship between filling particle radius and locking torque

由式（1）、式（12）、式（15）可知，颗粒阻塞囊的刚度k随着Pb的减小而增大，刚度仿真结果如图11 所示。

图11 颗粒阻塞囊刚度k 随Pb 的变换曲线Fig.11 Transformation curve of particle blockage capsule stiffness k with Pb

4 结论

（1）将折纸原理与颗粒阻塞变刚度原理相结合，提出了全新的变刚度折纸单元的设计方案。

（2）建立了变刚度折纸单元的静力学模型，推导出颗粒阻塞囊刚度的计算方法，以及填充颗粒半径、变刚度驱动器内负压强与颗粒阻塞囊刚度间的关系。

（3）使用颗粒阻塞原理设计的变刚度驱动器通过改变内部的压强实现自身变刚度，改变其填充颗粒的参数，如颗粒半径、颗粒硬度等，可以改变变刚度驱动器的最大刚度。

颗粒阻塞原理可以很好地弥补包括折纸单元在内的柔性单元或柔性关节刚度不足的缺点，后续可利用颗粒阻塞变刚度原理设计变刚度柔性关节，这样可以在保留柔顺性能的同时保证机构的刚度。