基于MPC 和PID 的无人驾驶车辆路径跟踪控制

2023-09-20周义棚杨威

农业装备与车辆工程 2023年9期

周义棚，杨威

（201620 上海市上海工程技术大学机械与汽车工程学院）

0 引言

无人驾驶车辆和车辆部件的电气化是汽车行业的热门话题，许多车辆部件已被电动装置取代，无人驾驶技术有利于提高车辆的通行效率和行驶安全性[1]。控制无人驾驶车辆沿期望路径行驶是最重要的问题，已有多种路径控制方法得以应用，如视觉伺服控制、滑模控制、模糊控制、线性二次调节器（LQR）和模型预测控制（MPC）用于路径跟踪[2-6]。相关研究中，冀杰等[7]构建了多约束模型预测控制（MMPC）系统用于车道变换路径跟踪，可以保证智能车辆在车道变换过程中的路径跟踪性能及操纵稳定性能；章仁燮等[8]提出一种基于条件积分算法的无人驾驶车辆轨迹跟踪鲁棒控制方法，根据车辆相对轨迹的非线性运动学关系，得到有界的车辆期望横摆角速度实现车辆相对轨迹的侧向位移误差的全局渐进稳定；辛喆等[9]针对极限轮胎-路面条件，提出约束车辆的前后轮侧偏角的模型预测控制方法，保证极限工况下无人驾驶车辆的行驶稳定性；张栩源等[10]提出了一种考虑前馈控制和转角补偿的线性二次调节器（LQR）和PID 的横纵向协同控制方法，在泊车和换道工况下验证了该方法的有效性。

本文考虑无人驾驶车辆在变曲率条件下的路径跟踪精度和稳定性，提出一种基于道路曲率车辆模型的MPC 横向控制器和双环PID 纵向速度控制器。MPC 横向控制器得到最优前轮转向角输入到无人驾驶车辆；双环PID 纵向速度控制器根据纵向速度误差环和纵向位置误差环控制无人驾驶车辆稳定快速地达到期望速度。

1 车辆横向动力学模型

本文采用考虑横向运动和偏航运动的改进单轨（自行车）动力学模型设计路径跟踪控制器。车辆动力学示意图如图1 所示。

图1 考虑路径曲率的车辆横向动力学模型Fig.1 Vehicle lateral dynamics model considering path curvature

图1 中：ey——横向误差；eφ——偏航角误差；δf——前轮转向角；θf、θr——前后轮侧偏角；lf、lr——质心到前后轮的距离；φ——横摆角；V——质心速度。

车辆具体参数如表1 所示。

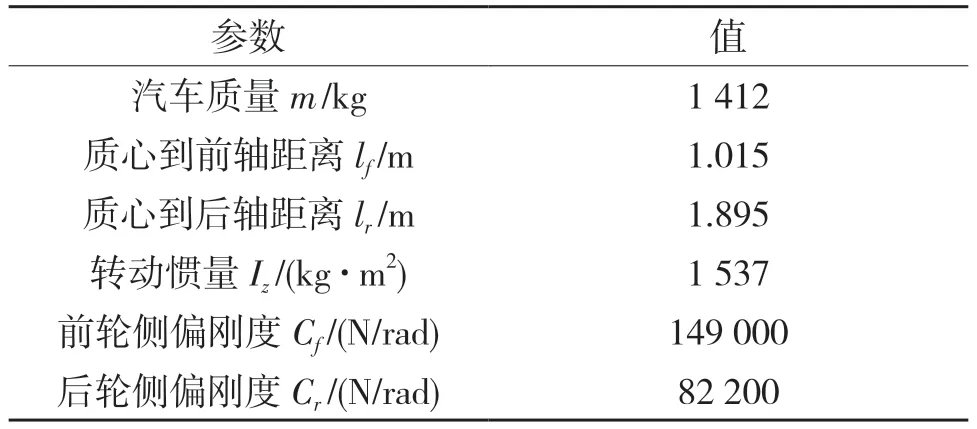
表1 车辆参数Tab.1 Vehicle parameters

2 MPC 横向控制器设计

MPC 常用于路径跟踪控制。基于小角度假设的车辆动力学线性模型，状态空间方程式（1）可以写为

对于MPC 控制器，通过求解满足目标函数以及各种约束的优化问题，在预测时域内求得最优控制序列，并将该控制序列的第1 个元素作为受控对象的实际控制量，重复上述的求解过程，实现对被控对象的持续控制。为了将模型应用于MPC 控制器的设计中，需要对式（2）进行离散化处理

在MPC 控制器中控制变量的变化速度对实际被控系统有较大影响，需要对控制量的增量进行约束限制，将式（3）变换为

可以得到新的状态空间表达式

n——状态量的维度；m——控制量的维度。

目标函数需要加入系统状态量的偏差和控制量作为优化目标，以保证无人驾驶车辆快速且平稳地跟踪参考路径。目标函数可以采用以下形式

式中：Q，R——权重矩阵；Np，Nc——MPC 的预测时域和控制时域。

本文主要考虑控制过程中的控制量极限约束和控制增量约束，控制量极限约束为

控制增量约束为

二次优化问题可用二次规划求解器求解，计算出最优转向角后，仅第1 个输出作为系统下一次采样时间的控制，优化问题在每个步骤内递归求解。

3 PID 纵向速度控制器

除了无人驾驶车辆的横向跟踪精度外，无人驾驶车辆速度控制的精度和平顺性也是自动驾驶的关键性能指标。行驶舒适性要求输出速度和加速度尽可能平稳，无需剧烈的制动/油门操作。速度控制器精度要求无人驾驶车辆的速度误差尽可能小。PID 控制易于实现，不依赖精确的车辆模型，可以降低无人驾驶车辆路径跟踪过程的总体计算量。本文采用纵向位置误差环和速度误差环的双PID 结构，设计无人驾驶车辆的纵向速度控制器，在满足跟踪精度的同时提高车辆行驶的平顺性。

本文在参考路径上建立Frenet 坐标系，如图2所示。车辆的实际位置A投影到Frenet 坐标系B上，本文假设离投影点B最近的离散坐标点C为无人驾驶车辆路径跟踪的参考路径点。

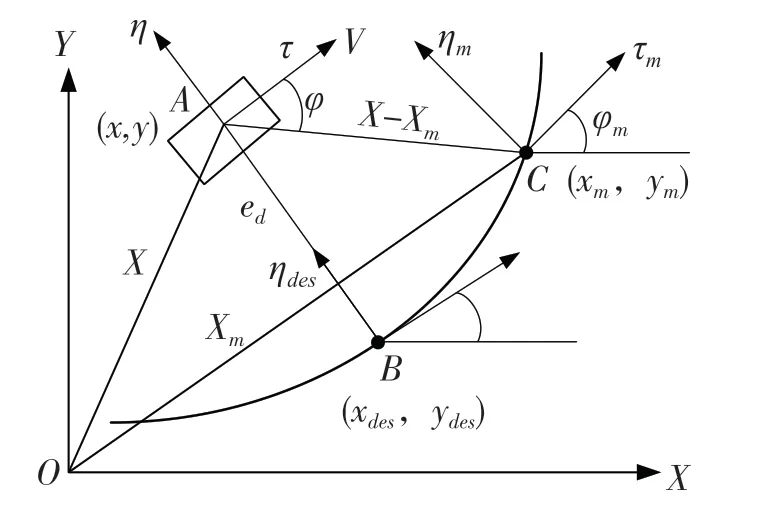
图2 Frenet 坐标系下的车辆误差模型Fig.2 Vehicle error model in Frenet coordinate system

由图2 可得

式中：τm——参考点C的切线单位向量；ηm——参考点C的法线单位向量。

式中：X——车辆实际位置A 的二维向量；Xm——最近参考点C的二维向量；d——车辆实际位置A到路径参考点C的向量之差。

纵向位置误差环中的误差量es和纵向速度误差环中的误差量ev分别为

式中：vref——无人驾驶车辆跟踪的目标速度；vdes——车辆投影到Frenet 坐标系上的速度。

双PID 纵向速度控制器的结构图如图3 所示。

图3 纵向速度控制器的结构图Fig.3 Block diagram of longitudinal speed controller

4 仿真实验与验证

为了验证所提MPC 横向控制器和双PID 纵向速度控制器的有效性和可行性，在CarSim-Simulink 联合仿真平台进行试验仿真和验证。采用双移线方程为参考路径，验证本文的控制方法在变曲率道路的路径跟踪效果，表达式为

图4（a）为双移线的路径位置，其路径点由式（15）求得；图4（b）为路径的参考航向角由式（16）求得。

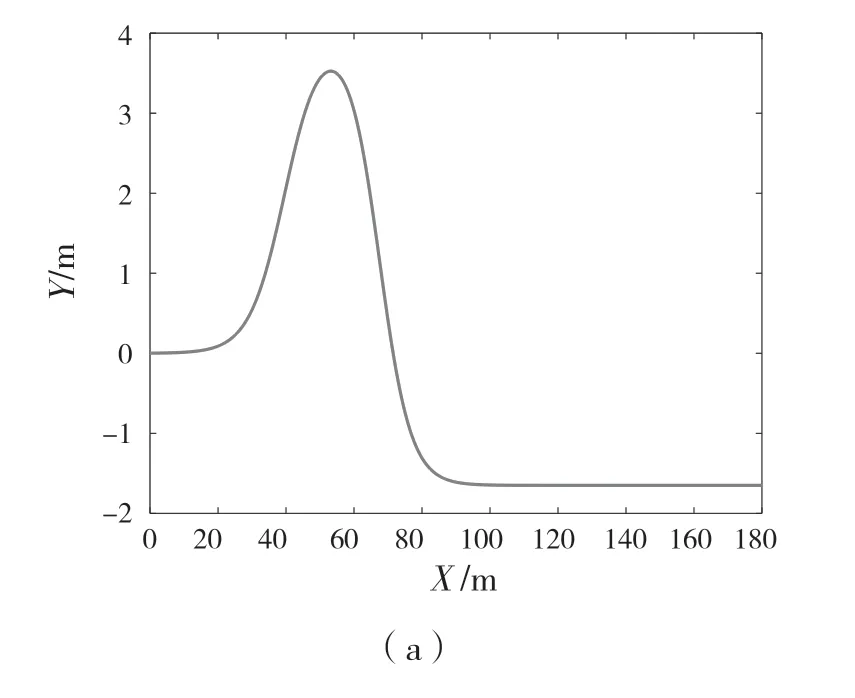
图4 参考路径Fig.4 Reference path

MPC 横向控制器的参数如表1 所示，车辆的基本参数如表2 所示。

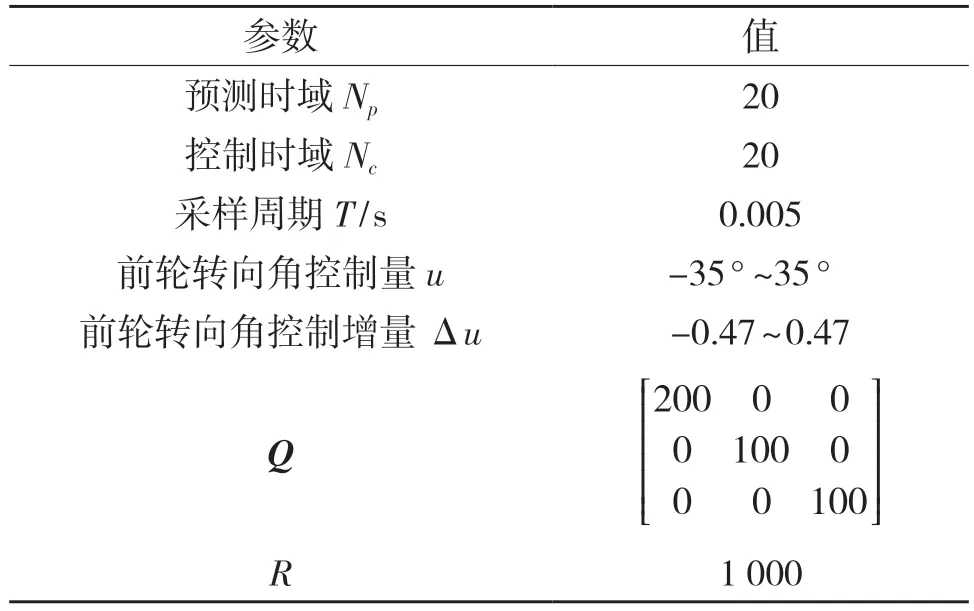
表2 MPC 控制器参数Tab.2 MPC controller parameters

本文在车速为20 m/s 的极限工况下对双移线路径进行路径跟踪仿真，并和LQR 路径跟踪方法进行了对比。LQR 路径跟踪方法可参考Xu 等的研究[11]。无人驾驶车辆在20 m/s 速度下跟踪参考路径（图4）的结果对比、仿真中MPC+PID 和LQR+PID 算法的路径跟踪效果对比如图5 所示，。

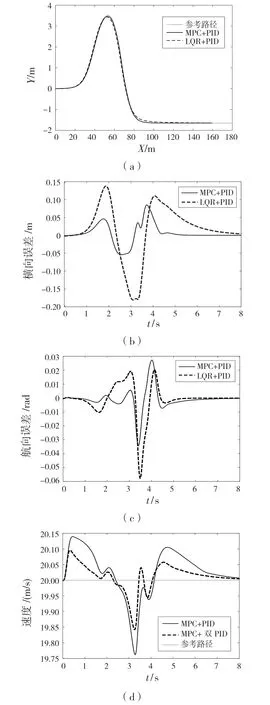
图5 20 m/s 工况下跟踪对比效果Fig.5 Tracking comparison effect under working condition 20 m/s

由图5（b）可知，在20 m/s 的极限速度工况下，无人驾驶车辆采用本文的MPC+双PID 控制方法的横向误差最大为0.085 m，而LQR 方法的最大误差是0.181 m。本文MPC+双PID 比LQR 方法在极限速度工况的横向控制精度可提高53%。在纵向速度控制方面，本文的双环PID 速度控制方法相较于普通PID 控制，在极限速度工况下速度跟踪误差从0.24 m/s 降低到0.16 m/s，速度跟踪精度可提高33%。横向控制精度提高是因为MPC 控制方法是在预测时域范围进行迭代优化的过程，可以在每个控制时域中使车辆的横向控制性能达到最优，而LQR 方法无法实现实时迭代优化。本文的纵向双PID 速度控制器，在考虑纵向速度环的基础上加入纵向位置误差环，可以降低纵向速度跟踪误差。