基于卷积神经网络-长短期记忆的施工期盾构管片上浮过程预测模型
2023-09-19苏恩杰李思翰张宏权
苏恩杰, 叶 飞, 何 乔, 任 超, 李思翰, 张宏权
(1. 长安大学 公路学院,陕西 西安 710064;2. 贝尔福-蒙贝利亚技术大学 信息学院,贝尔福 90000;3. 中铁十二局集团第一工程有限公司,陕西 西安710038)
盾构隧道施工方法具有机械化程度高、对地表扰动小、适用范围广、掘进速度快等优点,该工法在铁路、公路、市政、水力水电等工程的应用越来越广泛[1-2]。我国盾构隧道壁后注浆普遍采用凝结时间较长的单液浆,因此衬砌管片在离开密封刷后经常发生上浮现象,从而导致一系列的问题,包括盾构隧道轴线偏移、管片错台、管片破损及渗漏水等[3-4]。由于管片上浮的影响因素较为复杂,为了探究盾构管片上浮机理,许多学者针对此现象进行了研究。早期黄威然等[5]从地质条件、盾构工法、盾构机掘进姿态、壁后注浆以及设计等5 个方面对盾构隧道管片位移进行研究,并对施工阶段的盾构隧道管片漂移控制提出了建议;叶飞等[6]根据施工期管片上浮的特点,将盾构隧道管片上浮力分为静态上浮力和动态上浮力,分别分析其上浮机理,给出了管片上浮力的具体计算公式;肖明清等[7]使用有限元法对影响盾构管片上浮的地层特性、壁后注浆材料等因素进行了分析,结合管片在施工期的受力状态进行分析,对管片上浮的原因进行了阐述,并提出施工、设计不同阶段控制施工期管片上浮的措施;戴志仁[8]在考虑管片环间的纵向约束作用下,得到了维持盾构隧道管片抗浮稳定需要的浆液最小屈服强度表达式,并明确了浆液屈服强度对盾构隧道管片抗浮的作用;董赛帅等[9]通过现场实测结合理论分析,对施工期管片上浮规律进行研究,将施工期管片上浮分为两个阶段进行分析,并提出相应的对策和针对性措施;针对施工期管片上浮众多影响因素,黄钟晖等[10]采用敏感性分析法计算出各主要影响因素的权重排序,并分析各因素的作用机制,提出了针对性的管片上浮控制措施;吕乾乾等[11]考虑地基回弹的影响,建立隧道开挖动态模型,分析出了软弱地层的地层弹性模量与管片上浮量之间的关系;舒瑶等[12]统计了粉砂-圆砾、砂层、泥岩-粉砂质泥岩及粉质黏土等典型地层区段上浮量值的数学分布特征,分析了各典型地层段隧道上浮的主要原因,并利用纵向等效连续梁模型对各典型地层区段管片上浮量值进行预测;李明宇等[13]对大直径泥水盾构隧道管片在施工期间的上浮、错台以及收敛变形进行了监测,根据监测结果分析了盾构隧道横、纵向上浮分布特征,并提出管片上浮的控制措施;焦建林等[14]针对曲线段盾构隧道管片的上浮规律进行研究,分析不同地质及盾构机掘进姿态对管片上浮的影响,并提出了相应的盾构管片上浮综合控制措施。在盾构管片上浮预测方面,叶飞[15]将沿着隧道纵向隧道的管片环衬砌视为埋置在土层中的等效梁,通过在等效梁上表面设置地基弹簧约束模拟覆土作用地基及覆土对管片环的作用,由此建立了早期的管片上浮预测模型。张建勇[16]基于双面弹性地基梁理论、,修正纵向等效连续化模型以及浆液环向充填理论,在考虑上浮力时变性的基础上,构建了管片上浮预测模型。随着人工智能技术的发展,学者们也将其运用于预测盾构管片上浮,如高玮[17]根据现场监测大数据采用深度信念网络得到了到较为准确的地表沉降和管片上浮预测值。
综上所述,近年来许多学者针对盾构管片上浮问题开展研究,并取得了系列成果。但现有的上浮量计算模型仅考虑有限的数个参数的作用,未能较全面地反映盾构机掘进参数的影响。此外,由于现阶段常用全站仪等传统方法来监测管片上浮的情况,无法精确获得管片连续的上浮数据,故现有的相关成果仅对管片最终上浮量进行预测和对比,缺乏对施工期管片上浮过程的预测研究。基于此,本文采用动力水准仪对施工期盾构管片上浮过程进行自动化监测并提出了基于卷积神经网络-长短期记忆网络(convolutional neural networks and long shortterm memory, CNN-LSTM)深度学习算法的管片上浮过程智能预测方法。研究结果可为盾构管片上浮的现场监测及预防处治提供新思路。
1 管片上浮力学计算模型分析
目前管片力学分析主要分为局部管片竖向运动模型与隧道纵向弯曲变形模型两种。
(1)局部管片竖向运动模型
此类方法假定刚脱出盾尾时的上浮速度为零,此时管片受到的不平衡上浮力最大,上浮加速度也为最大值,管片开始上浮。随着浆液黏滞阻力、地层应力的不断增大,管片达到受力平衡状态后最终会停止上浮,如图1 所示。因此根据牛顿第二定律加速度a与合力F的关系,对时间积分可得到管片上浮速度v表达式,而速度v关于时间积分便可计算出管片竖向位移S,如式(1)—(3)。该方法虽然简单易懂,但由于相关竖向力较多(图中Ff为管片受到的浆液浮力、Fy为同步注浆产生的压力差、Ft为千斤顶推力的竖向分力、G为管片自重、Fn为管片受到的黏滞阻力、Fm为环间摩擦阻力、Fj为环间螺栓剪力),需要进行多处假设且常出现超越方程。此外该方法未能考虑不均匀推力等因素所产生的弯矩以及其对隧道整体纵向变形的影响。
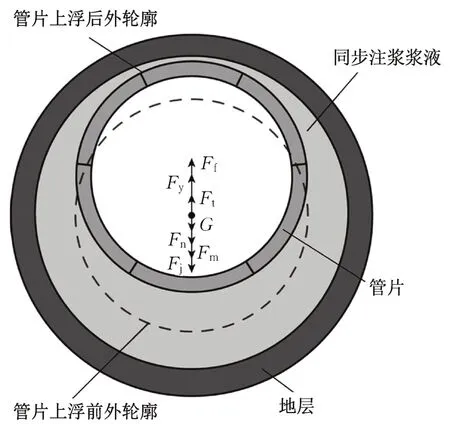
图1 管片受力示意图[18]Fig. 1 Schematic diagram of segment force[18]
(2)隧道纵向弯曲变形模型
基于小泉淳[19]提出的纵向梁-弹簧模型和志波尤纪夫[20]提出的纵向等效连续化梁模型,学者们提出了许多管片纵向上浮计算方法。如叶飞等[21]基于等效连续梁理论式(4)—(5),将隧道和土体的相互作用等效为土弹簧,提出了同步注浆产生的静态上浮力和动态上浮力作用下隧道结构的纵向变形计算模型。朱令等[4]、杨方勤等[22]、舒瑶等[23]、黄旭民等[24]考虑了同步注浆过程中浆液黏度时变性、上覆土体基床系数各异性、动态施工步的影响,进一步完善了隧道纵向变形计算模型(图2)。这类方法将盾构隧道管片复杂的三维受力简化为纵向的一维问题,将纵向弯曲变形视为隧道管片上浮量,虽便于计算但也忽略了盾构掘进参数的影响。此外由于常规的监测手段无法获得管片连续上浮数据,故无论是局部管片竖向运动模型还是隧道纵向弯曲变形模型均未得到有效验证,也无法解释本文所监测到的“阶梯状”上浮规律。鉴于目前上浮力学计算模型的局限性,且管片上浮受众多因素的影响,因此结合华东某盾构隧道掘进数据以及本文提出的管片上浮自动采集方法,采用人工智能中的深度学习算法,建立掘进参数与上浮过程之间的联系。
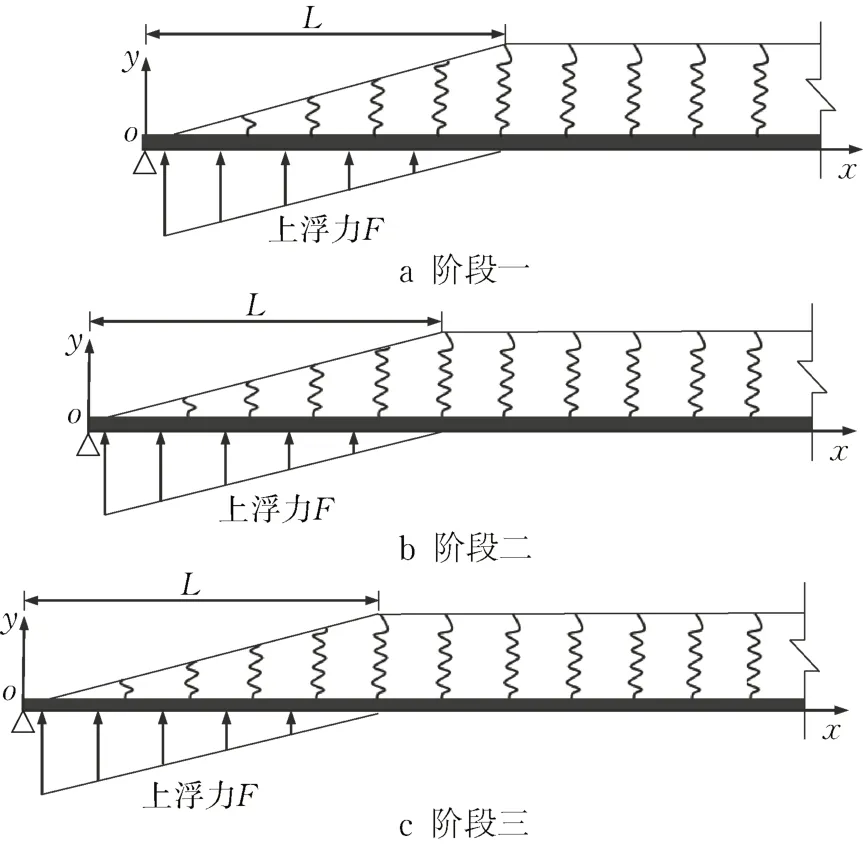
图2 施工动态示意图Fig. 2 Diagram of dynamic construction
式中:φ为弯曲后中性轴的位置角;Kb为连接螺栓的线刚度,Kb=EbAb/lb,Eb为螺栓弹性模量;Ab为螺栓横截面积;lb为螺栓计算长度;n为环间连接螺栓个数;Ic为隧道纵向惯性矩;Ec为管片弹性模量;Ac为隧道横截面面积;lc为相邻两管片环中心线间的距离,其大小近似于管片环宽B。
2 工程概况
华东某盾构隧道为双洞单线隧道,隧道主要穿越泥质砂岩地层,地层富水性及透水性均较弱,基岩裂隙水总体贫乏,地下水总体不发育,各地层物理力学特征见表1。隧道纵坡呈“W”区间,线间距12.0~43.1 m,隧道顶部埋深为6.43~26.74 m,共设5个联络通道,全长3 058.79 m,测试区间地质剖面如图3所示。

表1 地层物理力学特征Tab.1 Physical and mechanical characteristics of strata
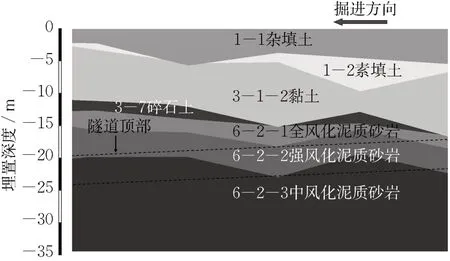
图3 地质剖面图Fig. 3 Geological section map
盾构区间采用刀盘直径 6 440 mm 的土压平衡盾构机,盾构机主要设备参数如表2 所示。盾构机上安装有数据采集系统,每隔1 min采集一次传感器参数和机器运行参数。隧道衬砌采用外径6 200 mm,内径5 500 mm,厚度350 mm 的C50 钢筋混凝土管片。管片环宽有1 500 mm 和1 200 mm 两种规格,均为通用楔形环,楔形量为37.2 mm。环向分块采用一块封顶块、两块邻接块、三块标准块。
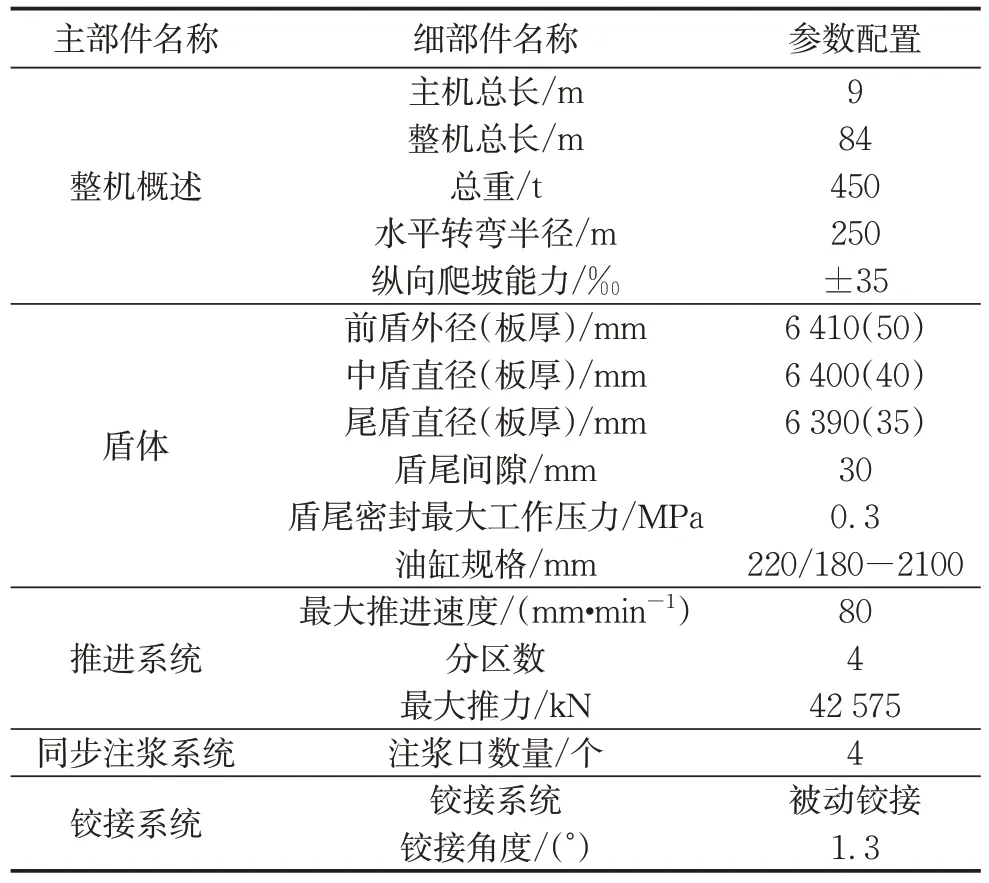
表2 盾构机参数配置表Tab.2 Parameters of shield machine
3 数据获取与处理
3.1 管片连续上浮数据
3.1.1 采集装置
采用AR-SS-SZY01 动力水准仪对管片上浮进行连续的自动化监测,它可在振动和运动环境下能准确地测量出竖向位移,测量精度为±0.5 mm,最高可支持30 Hz 的采集频率。配套的设备及材料有储液罐、网关采集器、水管、气管及电缆线(图4)。为了确保储液罐和基准水准仪安装在稳定的位置,将它们设置于脱出台车的管片上,距离盾尾75 m以上。

图4 试验装置Fig. 4 Test equipment
3.1.2 采集过程
(1)储液罐和基准水准仪安装:将储液罐和基准水准仪安装在不发生上的位置。
(2)装置串联成型:用水管、气管及电缆线将储液罐与水准仪、以及水准仪之间串联。
(3)排出气体:往储液罐中持续注入纯净水,将水管与水准仪中的气体排出,使整个系统处于无气泡状态。
(4)安装测点水准仪:待管片拼装完成后,将测点水准仪固定于待监测的管片内壁。
(5)数据自动采集:用电缆线链接基准水准仪与网关采集器,接通电源,自动采集与记录第269-271三环管片上浮数据。
3.2 掘进参数
盾构机自带的运行监测系统可采集设备倾角、刀盘转速、顶推工作状态、油缸推进压力、总推进力、油缸行程等157个参数,在除掉“人舱CO浓度”等与管片上浮相关性较小的参数后,选取刀盘驱动系统、推进系统、铰接系统等盾构掘进参数,经过筛减后的样本集中参数为36个,如表3所示。

表3 模型样本集中掘进参数Tab. 3 Tunneling parameters of model samples
由于篇幅所限,深度学习数据集以269环数据为主,收集盾构管片从脱出盾尾至稳定过程的掘进参数,样本容量为3 754个。
4 基于CNN-LSTM 的施工期盾构管片上浮预测方法
4.1 CNN算法
卷积神经网络(convolutional neural networks,CNN)是一类包含卷积计算且具有深度结构的前馈神经网络,由卷积层、池化层和全连接层组成,能自动提取数据特征并过滤输入数据噪声,可有效挖掘盾构掘进数据之间的相互关联并从中剔除噪声干扰[25]。
4.2 LSTM算法
长短期记忆网络(long short-term memory,LSTM)是一种时间递归神经网络,适合于处理和预测时间序列中间隔和延迟相对较长的重要事件。LSTM 算法引入存储单元,避免了传统的递归神经网络(recurrent neural network,RNN)的梯度消失和梯度爆炸问题[26]。如图5所示,存储单元由输入门、具有自递归连接的神经元、遗忘门和输出门这4 个主要元素组成(xt指第t个输入序列元素值;c指代记忆单元或称为细胞状态;i指代输入门;f指代遗忘门;ct-1指前一时刻的细胞状态;o指代输出门;ht-1指代在t-1时刻的隐层状态;ht指当前状态的输出)。输入门可允许或阻止输入信号改变存储单元的状态,输出门可允许或阻止存储单元的状态对其他神经元产生影响,遗忘门可以调节存储单元的自循环连接,允许单元根据需要记住或遗忘其先前状态[27]。虽然LSTM 可有效学习时间序列数据,但不能很好地从训练集中提取数据特征[28]
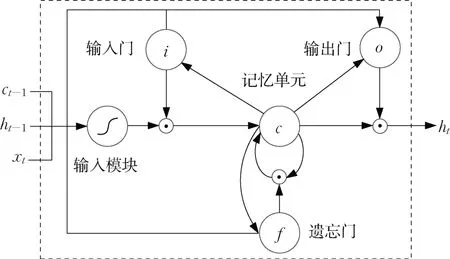
图5 LSTM模型结构图[29]Fig. 5 Structure diagram of LSTM model[29]
4.3 CNN-LSTM混合模型
在处理复杂事件时,单一神经网络算法在运算速度或性能方面往往具有局限性[30],因此多种神经网络结构组合的算法日益受到关注。CNN-LSTM算法既能发挥CNN 算法提取数据的空间特征和降低数据维度的长处,又能突出LSTM 算法擅长获取数据的时间特征、具有长期记忆功能的特点。本文所建立的CNN-LSTM 模型共5 层,包括一维卷积层、池化层、两层LSTM 层和全连接层(图6),模型参数见表4。

表4 CNN-LSTM模型设置参数Tab. 4 Parameters of CNN-LSTM model

图6 CNN-LSTM模型结构图Fig. 6 Structure diagram of CNN-LSTM model
5 验证与分析
5.1 数据划分
将样本集按7:3 的比例进行划分,其中训练集占比7/10,测试集占比3/10。由于盾构运行数据范围差异很大,为提高计算效率将训练和测试集中的36个输入参数和输出管片上浮均归一化至[0, 1]区间内。
5.2 模型评价指标
选用均方误差MSE、平均绝对误差MAE 和决定系数R2作为模型性能评估指标。
(1)均方误差MSE
式中:n为样本的个数;yi为真实值;ŷi为预测值;WMSE表示预测值偏离真实值的距离平方和的平均数。MSE 是一种反映预测值与真实值之间差异程度的度量,MSE值越小,模型的精准度越高。
(2)平均绝对误差MAE
WMAE表示模型预测值与样本真实值之间距离的均值。MAE 值越小,则代表预测模型的效果越好。
(3)决定系数R2
5.3 结果讨论
5.3.1 管片上浮连续规律
相邻的三环管片整体均呈现“上浮-稳定”的趋势,即管片脱出盾尾后先经历上浮增长较快,而后进入稳定状态(图7)。

图7 管片整体上浮规律Fig. 7 Integral floating law of segments
此外,在相同时间段不同管片上浮量变化过程较表现出一定同步性。进一步分析“上浮阶段”连续上浮规律,如图8所示。

图8 管片上浮阶段规律Fig. 8 Law of segments floating stage
图8 中黄色区域(浅灰)为盾构掘进状态,蓝色区域(深灰)为管片拼装状态,白色区域为待机状态。管片在脱出盾尾后呈现出“阶梯状”上浮的规律,即上浮主要发生在盾构掘进期间,上浮曲线为倾斜向上的增长趋势;在管片拼装状态,上浮无明显规律,如269环在前4个拼装期间为增长趋势,在第五和第六个掘进区间为水平趋势,270和271环的最后三个掘进期间为下降趋势;而在待机状态,管片上浮量较小,表现为近水平趋势。同时掘进状态的上浮量最大,其中269 环为27.90 mm,占比为75.24 %;270环为31.07 mm,占比为85.36 %;270 环为27.61 mm,占比为98.29 %(表5)。
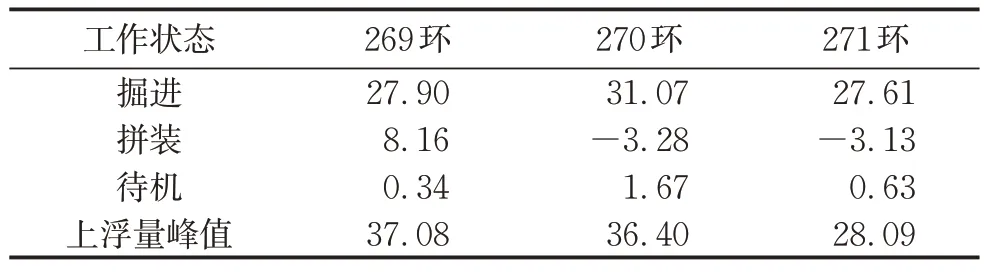
表5 不同工作状态管片累计浮量Tab. 5 Cumulative floating amount of segments under different working conditions
5.3.2 模型预测结果
模型训练使用的计算机环境配置如下:Windows 10(64 位),采用Intel Core I7-12700中央处理器,CPU 频率为2.4 GHz,内存为16 GB,编程语言采用Python 3.9,科学计算库采用Numpy 1.23.4,数据分析库采用Pandas 1.5.3,数据可视化库采用Matplotlib 3.5.2,机器学习库采用Torch 1.8.0,集成开发环境(IDE)为Spyder 5.1.5。
CNN-LSTM 模型及盾构施工领域使用较多的BP 模型(隐藏层神经元个数:64,隐藏层数:5,学习率:0.01,迭代次数:5 000,batch_size:32)在训练集和测试集上的预测效果如图9所示。
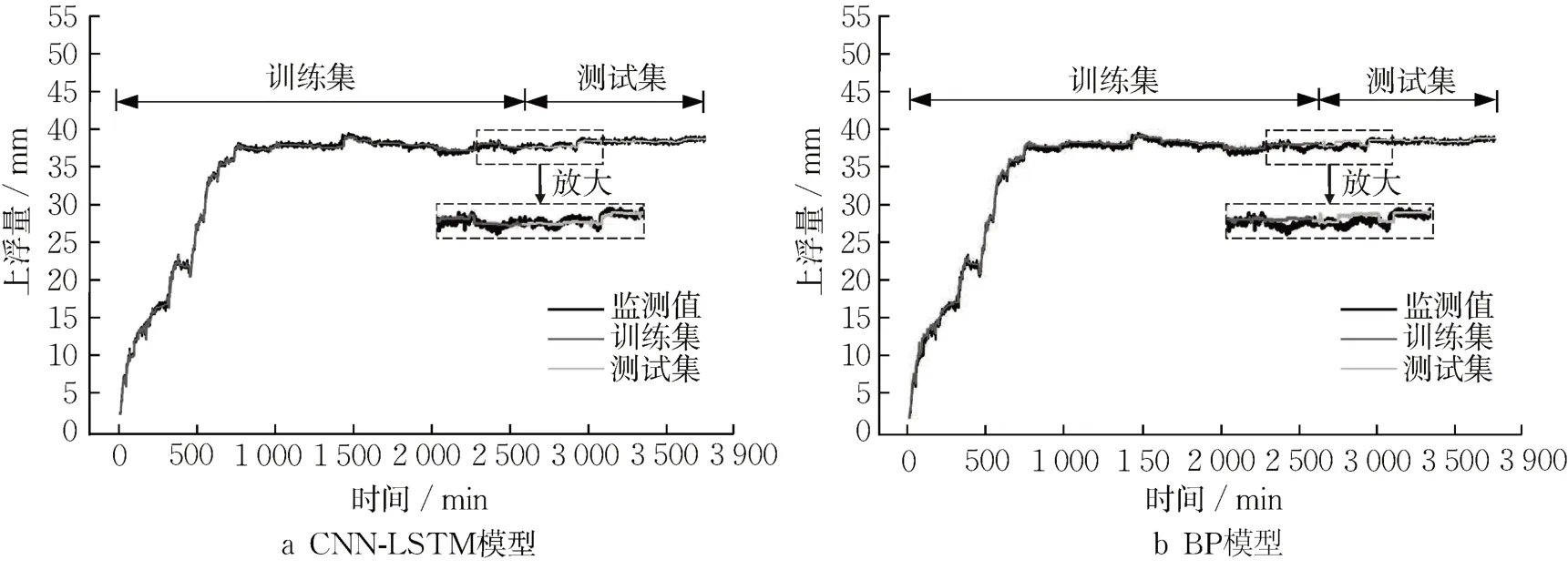
图9 两种模型预测效果对比Fig.9 Comparison of prediction effects of two models
由图9可知两种模型均能较好地实现施工期管片上浮过程的预测,但CNN-LSTM 模型的预测值整体更贴近监测值,所以其预测结果更好。
5.3.3 模型性能评估
选用均方误差MSE、平均绝对误差MAE 和决定系数R2作为模型性能评估指标。两种模型预测性能对比结果如图10所示。
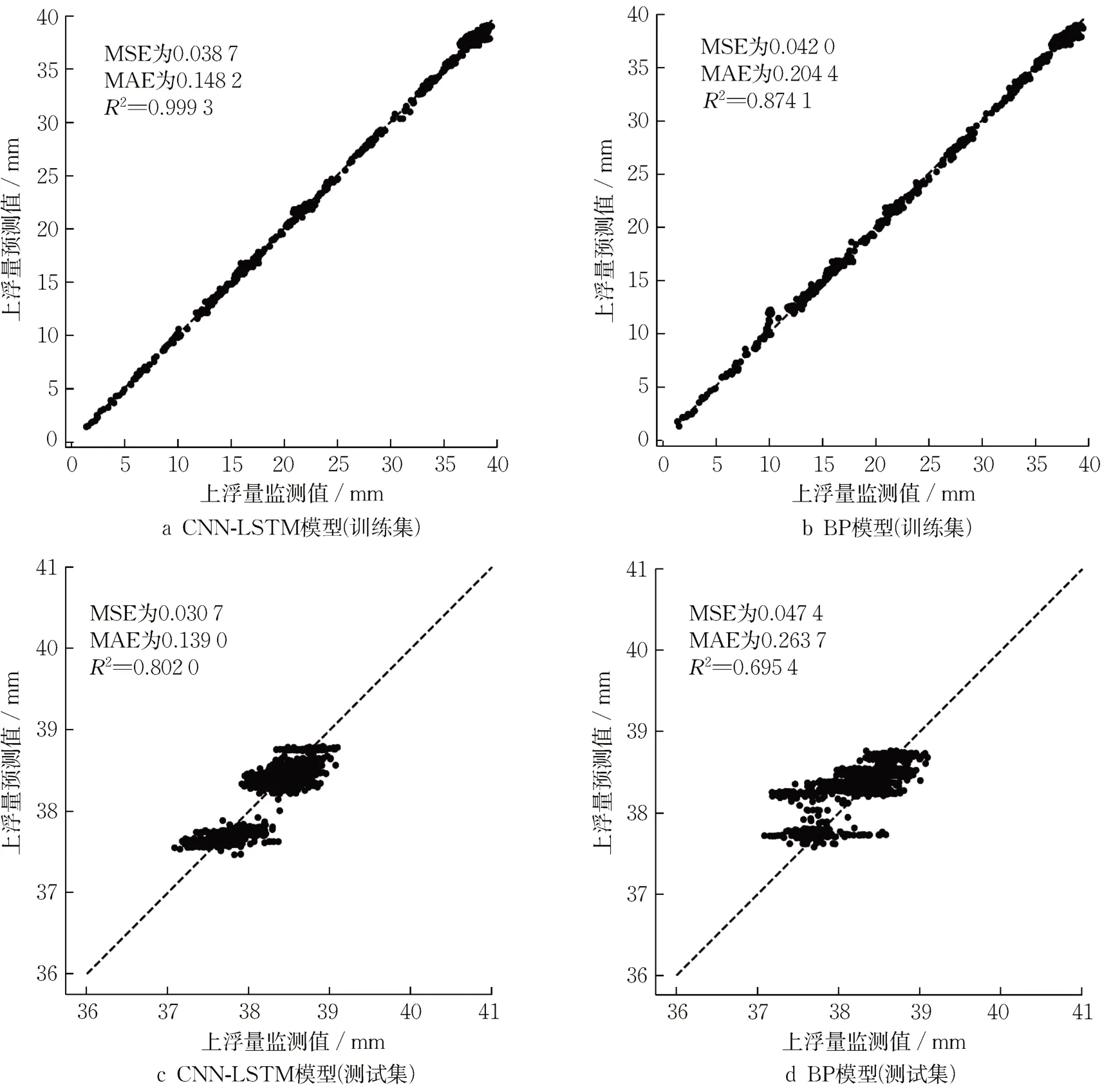
图10 不同模型的预测性能Fig. 10 Prediction of performance of different models
在训练集上,CNN-LSTM 模型的均方误差MSE、平均绝对误差MAE 和决定系数R2分别为0.038 7、0.148 2 和0.999 3,而BP 模型为0.042 0、0.204 4 和0.874 1。CNN-LSTM 模型各参数较BP模型提升8.53%、37.92%、12.53%。在测试集上,CNN-LSTM 模型的均方误差MSE、平均绝对误差MAE 和决定系数R2分别为0.030 7、0.139 0 和0.802 0,而BP 模型为0.047 4、0.263 7 和0.695 4。CNN-LSTM 模型各参数较BP 模型提升54.40 %、89.71 %和13.30 %。由此可知,CNN-LSTM 模型在训练集与测试集上的性能均比BP模型有所提升,且测试集的提升更明显。值得注意的是,训练集和测试集决定系数R2差别较大,其原因可能是测试集的数据近水平分布,预测结果稍有偏差便会对该指标造成较大的影响。
6 结论与展望
针对全站仪等传统方法无法获得施工期管片连续上浮数据的现状,本文采用动力水准仪自动监测施工期盾构管片上浮的完整过程,并建立CNNLSTM 模型对管片上浮进行智能预测。主要结论如下:
(1)管片整体均呈现“上浮-稳定”的趋势,即管片脱出盾尾后先经历上浮增长较快,而后进入稳定状态。上浮阶段呈现出“阶梯状”,即管片上浮主要发生在盾构掘进期间,该阶段上浮曲线为倾斜向上的增长趋势;拼装状态上浮无明显规律;待机状态,管片上浮量较小,表现为近水平趋势。同时掘进状态的上浮量最大,占峰值的75.24 %~98.29 %。
(2)本文所建立的CNN-LSTM 模型能结合CNN算法与LSTM算法的长处,对盾构管片上浮过程具有较好的预测性能。该模型在训练集上的均方误差MSE、平均绝对误差MAE 和决定系数分别为0.038 7、0.148 2和0.999 3,在测试集上为0.030 7、0.138 9和0.801 9。
(3)相较于BP模型,CNN-LSTM模型在训练集与测试集上的性能均有所提升,且测试集的提升更明显,最高可达89.71 %。
作者贡献声明:
苏恩杰:进行现场试验,建立预测模型及撰写论文。
叶飞:提出论文框架,指导论文修改。
何乔:软件调试和大数据分析。
任超:进行现场试验及数据整理。
李思翰:进行现场试验。
张宏权:协助完成论文内容。
