利用蒙特卡洛模拟评估TrueBeam加速器6 MV非均整模式下相空间文件的通用性

陈蕾，唐华南，傅玉川，李长虎，韩纪锋

1.四川大学华西医院 肿瘤中心 放射物理技术中心，四川 成都 610041；2.四川大学原子核科学技术研究所 辐射物理及技术教育部重点实验室，四川 成都 610064

引言

传统的医用直线加速器针对不同能量的X 射线适配了不同的均整器（Flattening Filter，FF）来得到均匀强度的射野。然而，目前常用的调强放射治疗技术是利用很多不同大小的子野叠加来得到更适形的剂量分布[1]，因此在光束的产生过程中均整器不再是必需的[2]。非均整（Flattening Filter Free，FFF）模式是指将加速器机头中的均整器去除后的出束模式。与传统FF 光束相比，FFF 束不仅具有不同的光束轮廓和更高的剂量率，还拥有不同的光子能量光谱和头部散射特性[3]。对单次高剂量的立体定向放射治疗（Stereotactic Radiotherapy，SRT）有较好的剂量学优势[4-5]。关于医用直线加速器FFF 模式下的剂量学特性和临床应用，已有较多基于蒙特卡洛（Monte Carlo，MC）的研究[6-7]。

对于介质内剂量沉积的MC 模拟，一般可分为针对加速器头的模拟和针对模体的模拟两个部分。加速器头中位于次级准直器之上的组件均较为固定，因而有研究者提出可以将其再分为两个部分，从源到次级准直器之上的部分和射束离开次级准直器之后的部分[8]。从源到次级准直器之上的部分只需进行一次模拟计算，获得的粒子相空间文件（Phase Space File，PSF）可作为后续部分的输入源，从而节省模拟计算的时间。目前可直接使用的PSF 均采取了国际原子能机构（International Atomic Energy Agency，IAEA）提出的格式[9]。Varian官方也提供了TrueBeam 型号加速器头的PSF，其可行性已获得了验证[10-11]。

基于此，为验证该PSF 的通用性和可靠性，本文以我院的1 台Varian Edge 加速器中的组件参数为基础，通过MC 程序EGSnrc 分别模拟完整的加速器头模型和使用PSF 作为输入源的部分加速器头模型，在FFF 模式下水模体中的剂量分布，对模拟计算获得的百分深度剂量（Percentage Dose Depth，PDD）、横向剂量离轴比（Off Axis Ratio，OAR）以及能谱进行比较，旨在探讨TrueBeam 的6 MV FFF 模式下PSF 对同类加速器的通用性。

1 材料与方法

1.1 测量数据

虽然Varian Edge加速器相比于TrueBeam有更先进的图像技术、六维治疗床和更精细的多叶准直器叶片，但二者的射束参数和特性基本一致[12]。本研究基于48 cm×48 cm×35 cm的水箱，采用灵敏体积0.125 cc的电离室探测器测量了射野尺寸为5 cm×5 cm、10 cm×10 cm、20 cm×20 cm、30 cm×30 cm，源皮距（Source to Surface Distance，SSD）100 cm时的PDD和深度为10 cm时的OAR。

1.2 MC模拟

1.2.1 完整的加速器机头的模拟

完整的加速器机头模拟（完整FFF 模型）中各组件及参数参考Varian 官方数据库，模型图如图1 所示，包括靶、初级准直器、Be 窗、均整器、监测电离室、灯光野镜和上下两对次级准直器。其中靶材料与几何设置与6 MV FF 模式相同。均整器部分采用1 块0.2 cm 的铜片代替以减少韧致辐射，PSF 在距离辐射源100 cm 处的相空间平面收集。MC 模拟程序为EGSnrc/BEAMnrc。

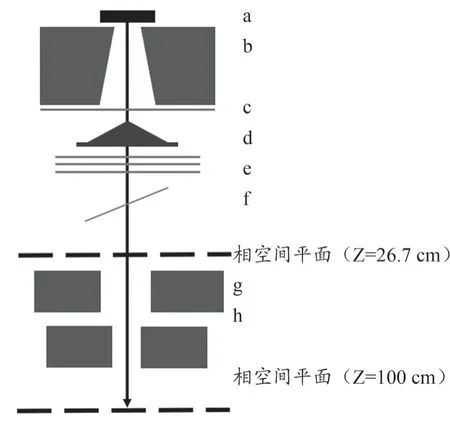
图1 加速器模型示意图

通过不断调整源参数，直至与水箱测量数据具有一致性，模拟PDD 与OAR 结果，最终确定射束入射电子能量为6.1 MeV，半高全宽为0.2 cm。

1.2.2 针对PSF的部分加速器机头的模拟

PSF 的部分加速器机头的模拟（部分FFF 模型）参考Varian 提供的TrueBeam 6 MV FFF 的PSF 在距离源26.7 cm 的相空间数据，每个文件约1 G，包含6.5×108个入射粒子。根据该PSF 的头文件和Varian 虚拟平台的参数，该射束电子入射能量为5.9 MeV，半高全宽为0.18 cm。考虑到计算机的储存能力，本文仅将其提供的前21 个文件组合作为输入源于26.7 cm 处入射。模拟模型包括次级准直器及其之后的部分，同样于距离辐射源100 cm 处的相空间平面收集数据。

1.2.3 模拟的参数设置

在EGSnrc/BEAMnrc 程序上模拟获得上述4 个射野在两种模式下的PSF 文件，然后使用EGSnrc/DOSXYZnrc 程序计算水模体中的剂量分布，计算中设置的水模体大小与测量水箱一致，体素大小为0.2×0.2×0.2 cm3。在BEAMnrc 和DOSXYZnrc 中电子和光子的截止能量分别为ECUT=0.7 MeV，PCUT=0.01 MeV，PRESTA- Ⅱ为电子步长算法，PRESTA-Ⅰ为电子边界算法。采用轫致辐射方向分裂（Directional Bremsstrahlung Splitting，DBS）方法增加计算效率，分裂数设置为1000，以最大化光子通量的效率。在BEAMnrc 中获得的PSF 均包含约109个粒子信息，DOSXYZnrc 的模拟粒子数均为109，且未重复使用PSF，使MC 模拟的不确定性小于1%。模拟在个人计算机上进行，配置如下：操作系统Ubuntu 20.04.5 LTS×86_64，CPU 型号Inter core i7-10700 (16) @ 4.8 GHz，GPU 型号NVIDIA GeForce GT 730.

1.3 差异分析方法

模拟获得的PDD 均在最大剂量点归一化，OAR 在中心轴处归一化。通过计算的测量剂量（Dref）和MC模拟剂量（Dsim）之间的局部百分偏差（Local Dose Difference，ΔD）[13]来评估PDD 和OAR 的差异，该偏差表示为每个点局部剂量差的百分比，具体计算方式如公式（1）所示。同时采用EGSnrc/BEAMdp 对模拟得到的10 cm×10 cm 射野下的PSF 的能谱和能量注量进行分析。

2 结果

2.1 光子线在水模体中PDD比较

4种射野下完整FFF模型和部分FFF模型的PDD和与测量数据相比的ΔD如图1所示，二者在靠近水箱表面处的剂量均与测量数据存在较大的ΔD，最高可达24.93%。完整FFF模型的射野5 cm×5 cm、10 cm×10 cm的PDD均与测量数据有较好的吻合性，ΔD均小于2%；20cm×20 cm除末端0.2 cm的ΔD差异可达5.77%外，均小于5%；30 cm×30 cm的PDD在深度31.7 cm前的ΔD均小于5%，最大差异可达6.27%。部分FFF模型的ΔD均大于完整FFF模型，5 cm×5 cm、10 cm×10 cm、20 cm×20 cm、30 cm×30 cm射野末端差异分别高达6.01%、6.70%、8.99%、9.53%，且20 cm×20 cm和30 cm×30 cm的ΔD分别在28.0 cm和27.7 cm处开始超过5%。

2.2 光子线在水模体中OAR比较

4种射野在深度10 cm处完整FFF模型和部分FFF模型的OAR和与测量数据相比的ΔD如图3所示，完整FFF模型和部分FFF模型的剂量平坦区与测量数据均吻合较好，差异小于1%，但在剂量跌落区存在较大的差异。当射野大小为5 cm×5 cm时，完整FFF模型和部分FFF模型的ΔD均较大，高达21.64%和23.24%。射野较大时，部分FFF模型的ΔD大于完整FFF模型，二者的最大差异分别为14.36%和18.69%（10 cm×10 cm）、15.46%和20.83%（20 cm×20 cm）、13.40%和14.77%（30 cm×30 cm）。

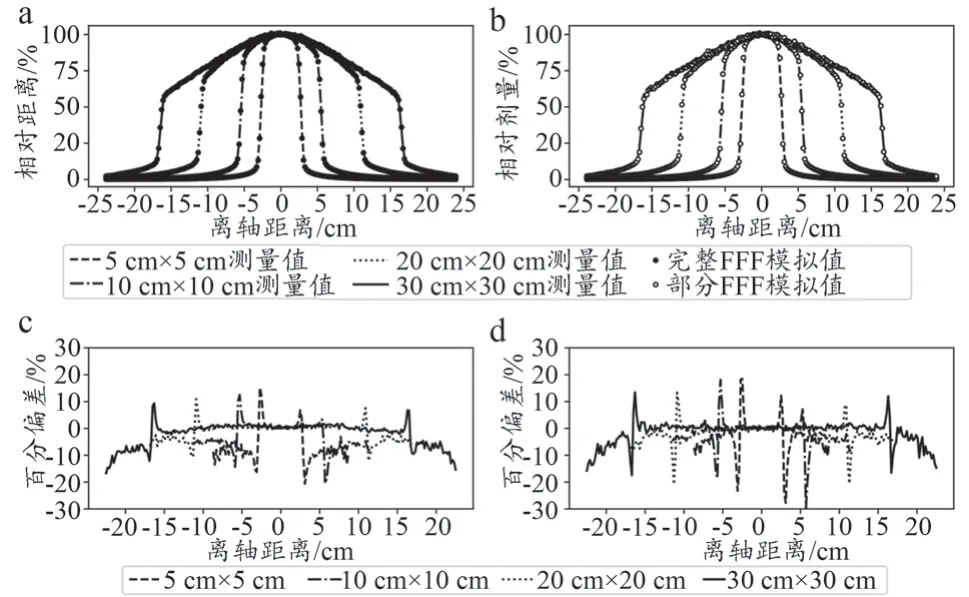
图3 不同射野下完整FFF模型和部分FFF模型的OAR和对应的ΔD

2.3 同一射野内光子线的能谱比较

通过完整FFF 模型和部分FFF 模型在10 cm×10 cm射野的PSF 分析得到的沿中心轴和离轴的能谱和能量注量分布如图4～5 所示。由图4a 和图5a 可知，能谱主要由光子、电子、正电子组成，且三者存在数量级的差异。在图4a 中心轴上的能谱分布中，二者的电子和正电子的能谱基本一致，但部分FFF 模型的低能光子注量略高于完整FFF 模型。由图4b 可知，部分FFF 模型中的低能粒子注量更高，但高能粒子注量低于完整FFF 模型。而在图5a 中，离轴方向上，二者的光子和正电子的能量注量基本一致，完整FFF 模型的电子注量略高于部分FFF 模型。由图5b 可以看出，完整FFF 模型和部分FFF 模型在离轴上的平均能量在中心处分别为1.27 MeV和1.17 MeV，部分FFF 模型整体上均低于完整FFF 模型，且跌落区跌落速度更快。

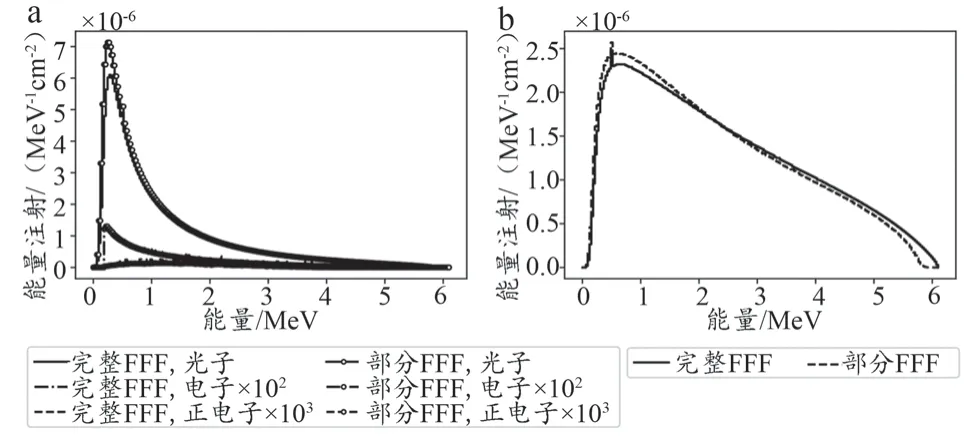
图4 10 cm×10 cm射野下不同粒子的能谱分布和总的能量注量分布

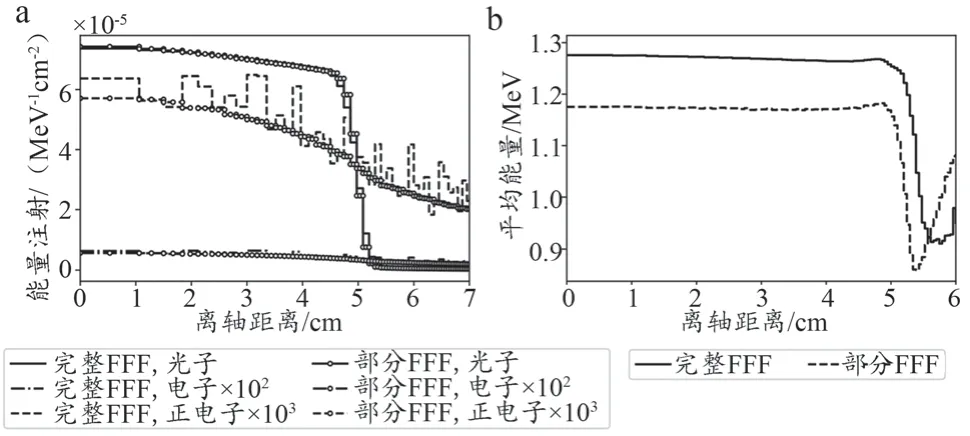
图5 10 cm×10 cm射野下不同粒子的离轴能量注量分布和总平均能量分布

3 讨论

MC 算法能够模拟复杂的加速器模型和患者模型，并且被公认为针对复杂患者几何形状和组织异质性的最准确的剂量计算方法[14]。随着计算速度的提升，MC 可用于临床计划的剂量计算和调强放疗的剂量验证。在放疗计划系统的射束建模中，PDD、OAR 和射线质指数是非常关键的参数，通过MC 模拟值与测量值进行对比验证，才可以得到准确的MC 模型，从而实现准确的剂量计算。

研究表明，部分FFF 模型的PDD 随着深度的增加，存在对测量数据的低估，这可能是因为Varian 提供的6 MV FFF 的PSF 存在对入射粒子能量的低估，入射电子的能量较低时，会出现PDD 尾部的跌落[15]和中心轴平均能量的低估。Belosi 等[10]利用Varian 的PSF 文件模拟时，也发现实验数据随着深度增加差异增大，且射野越大差异越大。有研究发现，MC 模拟中电子入射能量会影响PDD 与测量数据的匹配，而扩散角和半高全宽则会影响OAR 的形状[16-17]。因此，在多次调整入射能量后，将完整FFF 模型的电子入射能量提高到6.1 MeV，可使靠近末端的PDD 与测量数据的差异减小，出现与测量数据更好的匹配效果。

在进行小野（5 cm×5 cm）模拟时，为获取足够的粒子信息以避免计算水模体剂量时重复使用在距离辐射源100 cm处收集的PSF，会重复使用Varian提供的PSF，因而会造成不确定性的增加[18]，使得5 cm×5 cm的PDD差异较大。而在进行大野（20 cm×20 cm、30 cm×30 cm）模拟时，因水模体中的散射随着深度增加[19]，导致末端剂量差异逐渐增加。从能谱分析中，也可看出部分FFF模型中高能粒子不足，从而影响PDD的分布。而在部分FFF模型中，低能光子的占比较高，原因可能是初级准直器的开口较大，对低能光子的屏蔽较少[20]。根据Mamballikalam等[21]利用不同探测器测量的表面剂量和MC模拟数据对比，发现测量数据均存在高估，因此PDD靠近浅表的ΔD均较大。

完整FFF 模型和部分FFF 模型的OAR 在剂量平坦区均表现良好，原因为OAR 主要受到入射射束的半高全宽和平均角展影响[17]，但均在剂量跌落区对测量数据存在低估，尤其是在5 cm×5 cm 时，原因可能是采取传统的电离室探测器，受体积效应影响，在测量剂量跌落区时，其跌落较慢[22]。而在较大射野时，部分FFF模型的剂量跌落区差异略大于完整FFF 模型，可能由于离轴平均能量跌落较快。

本研究结果表明，完整FFF 模型和部分FFF 模型之间存在差异。通过比较两个模型的PDD 和OAR 数据，发现部分FFF 模型的结果略差于完整FFF 模型。此外，能谱分析也表明，部分FFF 模型的较低入射电子能量会对低能光子占比和离轴平均能量产生影响。需要注意的是，PSF 文件与实际加速器的测量数据存在差异，因此应谨慎使用。

4 结论

本研究使用MC 软件对利用Varian 提供的TrueBeam 的6 MV FFF 的PSF 构建部分FFF 模型和完整FFF 模型进行模拟，得到不同射野下水模体的三维剂量分布，并分析10 cm×10 cm 下距离辐射源100 cm 处收集的PSF 的能谱和能量注量，结果显示，采用PSF构建的模型存在PDD 偏低、OAR 偏差大、离轴平均能量低估等问题，主要原因为PSF 存在对高能能量的不足，以及受射野大小的影响。因此，建议采用Varian 提供的PSF 时，应进行验证，并在小野研究时组合足够多的PSF 以提高模拟准确性，在大野研究时应降低散射影响以提高准确性。构建完整的FFF 模型以适配水箱数据更具有灵活性，以适应不同的研究需求，同时能够节约模拟时间，避免数据不确定度的增加和无法匹配具体的水箱数据等问题。因此，为获得更准确的结果，建议在进行放射治疗计划设计时，应优先考虑采用完整的FFF模型。