单通道通信信号盲分离方法的研究进展综述

邓文，黄知涛，王翔

（1.国防科技大学电子科学学院，湖南 长沙 410073；2.国防科技大学电子对抗学院，安徽 合肥 230088）

0 引言

随着电子信息技术的迅速发展，用频设备数量呈爆炸式增长。信息传输系统经常处于时域高度密集、频域严重重叠、空域相互交织且随时间动态变化的复杂电磁环境中，导致各种电磁信号严重混叠。这给信息接收方的信号处理任务带来了巨大挑战。例如，2.4 GHz 频段是国际通信联盟无线电通信局规定的工业、科学和医疗（ISM,industrial scientific medical）频段，允许各个国家开放使用。基于IEEE 802.11 标准的无线局域网设备及蓝牙设备都工作在这一频段，当它们在同一狭小空间范围内同时工作时，二者的接收端都会接收到时频严重混叠的干扰信号[1]。在卫星通信领域，如星载船舶自动识别系统（AIS,automatic identification system）[2]等，转发干扰是很难处理的一种信号，因为它与通信信号频率相同，且统计相关，而功率往往比通信信号大很多，严重影响正常通信[3]。此外，基于成对载波多址（PCMA,paired carrier multiple access）的通信系统允许不同终端基于完全相同的频率、时隙及扩频码相互通信[4]。对该类信号进行侦察时，很难对同一链路中来自不同通信终端的信号进行参数分析及信息提取。面对这些复杂情况，传统的时频域滤波方法无法发挥作用，而在只有一个接收天线的单通道情况下，基于波束成形的空域滤波方法也将失效。因此，迫切需要一种可以有效应对多信号时频混叠场景的新技术，从而提升各类系统对复杂电磁环境的适应能力。

盲信号分离（BSS,blind signal separation）是解决复杂电磁环境下混叠信号处理问题的一种很有前途的技术。BSS 技术可以在传输信道参数未知的情况下，仅基于对期望信号较少的假设条件（如非高斯性、统计独立性、循环平稳性、稀疏性等），实现混叠信号分离[5]。BSS 技术对混叠信号的频谱关系没有要求，信号可以是不同频率的，也可以是同频率的，这对时频域高度混合的信号的处理非常有吸引力。然而，BSS 的理论框架是建立在传感器数目不小于源信号数目的基本假设之上的。在实际应用场景中，一些通信系统由于受到体积、成本等方面的限制，信号接收端往往只有一个接收天线，因此单通道观测条件下的 BSS（SCBSS,single channel BSS）技术研究将更具有现实意义。为此，研究人员在这一领域做了许多探索工作。

此外，随着计算硬件的不断发展和深层网络训练方式的优化，深度神经网络在许多数据处理领域表现出了强大的复杂问题建模能力和优异性能。近年来，深度学习（DL,deep learning）技术[6-7]在语音信号处理、自然语言处理等领域表现出优异性能[8-13]，在通信信号处理领域也出现了基于数据驱动技术的算法[14]，如信号检测[15-16]、调制识别[17-18]、信道估计[19]等。而基于数据驱动的SCBSS研究目前仍处于起步阶段。对于SCBSS 而言，DL技术为突破传统SCBSS 方法模型优化难、计算复杂度高、分离性能差等局限性提供了一种新的手段，即利用海量的数据寻找和建立信号内部特征关系，进而完成问题求解。数据驱动方法不需要考虑通信信号模型，而是将深度神经网络（DNN,deep neural network）视为黑盒，通过大量数据实现非线性拟合，训练完成的网络模型仅需要一次前向计算便可实现分离，弱化了模型失配带来的影响，同时避免了复杂的模型优化和参数选取过程。因此，基于数据驱动的SCBSS 是一个极具应用前景的研究方向。

本文将对单通道观测条件下通信信号盲分离的工作进行分析和总结，并在此基础上，综述现有基于数据驱动的SCBSS 研究现状，并探讨该技术目前亟待解决的问题和解决思路。最后，本文将展望SCBSS 未来的发展趋势，旨在帮助后续研究人员更好地理解基于数据驱动的SCBSS 技术，并为其提供相关思路，以促进该领域的进一步发展。

1 SCBSS 问题模型

其中，A(·) 表示广义混叠信道，决定了各信号与其在观测中对应分量的关系；v(n) ∈C1×1表示观测通道内存在的噪声及扰动成分。

BSS 问题中的“盲”强调的含义如下：1) 参与混叠的信号未知；2) 混叠信道未知。严格意义上的BSS 指的是在这2 个条件下，仅基于混叠观测完成对其中包含的所有信号的分离的过程。具体而言，其核心在于寻找某个分离系统W(·)，使仅以x(n)为输入的该分离系统的输出y(n)是s(n)的良好估计即满足

SCBSS 基本流程如图1 所示。

图1 SCBSS 基本流程

BSS 问题的分类可以根据研究问题的角度和所关注问题场景的不同而灵活设定多种标准。BSS 问题分类框架如图2 所示。现有的BSS 问题分类标准包括接收通道数、混叠信道类型和目标信号类型。多通道BSS 可以根据接收通道数M与信号数N的关系进一步划分为超定BSS（M＞N）、正定BSS（M=N）和欠定BSS（2≤M＜N）。根据是否考虑同一信号到达不同通道的时延差异以及同一信号到达同一通道的多径效应，线性混叠信道可以被划分为3 种：线性瞬时混叠信道、线性时延混叠信道和线性卷积混叠信道。

图2 BSS 问题分类框架

BSS 的目的是从混叠观测中恢复各个期望信号。一般而言，用期望信号的估计值与真实值进行对比，以评价算法的性能。根据应用场景的不同，分离系统输出恢复的信号形式一般分为信号波形和信号符号序列。因此，现有BSS 算法的性能评价指标可分为波形恢复质量评价指标和符号序列恢复质量评价指标两类。表1 展示了BSS 算法的性能评价指标。在不同场景下的分离系统中，需要选择相应的评价指标，以更准确地评估分离算法的性能。同时，也可以结合多种评价指标进行综合评价，以更全面地了解算法的性能表现。

表1 BSS 算法性能评价指标

2 SCBSS 技术研究进展

本节首先介绍基于应用逻辑的BSS 技术分类框架，然后详细梳理SCBSS 技术的研究进展，并分析当前研究中存在的不足。重点关注以时频混叠的数字通信信号为分离目标信号的现有SCBSS技术。

2.1 基于应用逻辑的BSS 技术分类框架

在严格的BSS 问题中，通常要求分离系统输出目标信号的时域波形，其中包含较完整的目标信号信息。然而，在实际BSS 系统中，输出结果的形式会因目标信号类型和具体信号分析/信息提取需求的不同而发生相应的变化。具体而言，一方面，信息的完整性意味着对信号时域波形的精确获取（恢复）往往难度较大；另一方面，实际BSS 应用对输出结果的后续分析或信息提取一般只关注某一方面或某一维度的目标信号信息，例如，参数分析中的谱峰信息或合作通信中的数字通信信号调制符号信息，而时域波形中包含的完整信息将大概率存在冗余或无用的部分。

具体而言，在频谱管理和特定信号检测等应用中，分离系统输出结果中所包含信号的参数信息（如载频、带宽和调制样式等）更受关注。为了满足获取该层次目标信号信息的需求，通常首先获取其时域波形，然后采用经典参数估计算法基于时域波形估计信号参数。而在合作/非合作通信中的一些典型BSS 问题场景下，相较于目标信号参数信息，更多关注的是数字通信信号调制符号信息。上述场景常见于以下三类典型BSS 问题中。

1) 合作通信中的通信抗干扰问题。由于合作通信的重点在于实现通信信息的传输，且目标信号参数均已事先准确获知，因此直接基于混叠观测对目标信号符号序列进行估计（分离）将更具有实际意义。

2) 非合作通信中的公开样式信号侦察问题。在对AIS 信号或其他格式固定且公开的目标信号进行侦察时，对其信号参数的估计无法带来有效信息增量，同时更多情况希望基于已知信号参数及格式对其中加载的调制信息进行解译，因此进行BSS 时的分离输出一般为直接对目标信号符号序列的估计[20]。

3) 非合作通信中的特定信号控守侦察问题。在此类问题中，由于持续关注特定目标信号，且前期已对其开展了充分的参数估计、样式分析等工作，因此在后期对同一目标信号进行BSS 时，往往不再关注其信号参数，而将进一步尝试获取其搭载的调制信息。

因此，分离系统的输出形式应针对不同的应用需求进行定制化处理，而非仅限于获取时域波形，以便更好地提升分离质量和效率。而这一般有助于降低分离难度，同时拓宽问题解决思路。

综上，BSS 技术可以根据分离系统的应用逻辑进行分类。一般而言，分离系统的输出形式应该与后续信号分析/信息提取中主要关注的目标信号信息层次和内容匹配。当目标信号为数字通信信号时，BSS 任务可根据分离输出形式大致分为2 种：波形分离和符号序列分离。前者指分离系统输出时域波形形式的情况，后者则指分离系统直接输出符号序列形式的情况。

基于应用逻辑的BSS 技术分类框架如图3 所示。多通道BSS 算法通常基于信号的统计独立性、稀疏性等假设，对不同类型的信号具有一定的普适性。这是因为多通道观测提供的信息相对充分，可以在关于目标信号的弱先验信息的帮助下完成信号分离。相比之下，SCBSS 算法仅基于单通道观测，因此需要更强的关于目标信号本身的先验信息来支持信号分离。这种先验信息可以作为对单通道观测条件下缺失的空间信息的补充。因此，在SCBSS中，对目标信号特性的分析和利用更重要。此外，SCBSS 算法在适用的目标信号类型方面具有更强的针对性，但也意味着较难从基于先验信息/假设角度对SCBSS 算法进行系统性的划分。

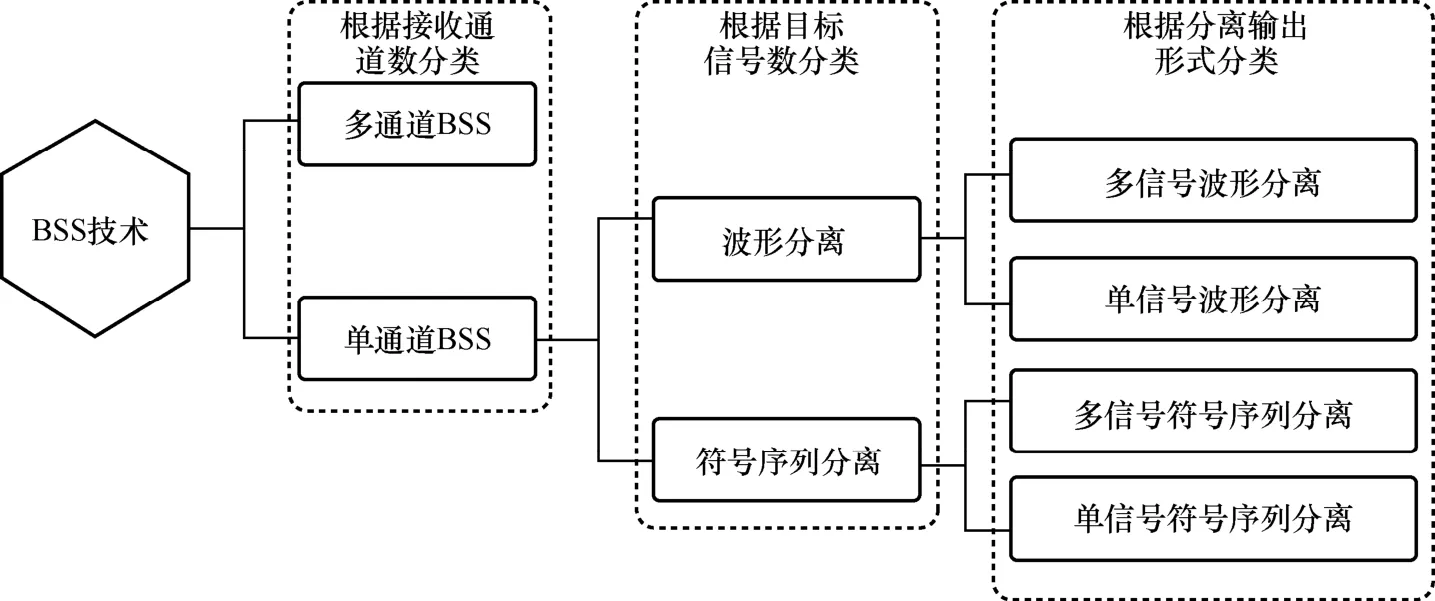
图3 基于应用逻辑的BSS 技术分类框架

本文主要关注单通道观测条件下的BSS 问题。根据新的分类框架，SCBSS 问题可被分为四类子问题，分别为：单通道观测条件下的多信号波形分离、单通道观测条件下的单信号波形分离、单通道观测条件下的多信号符号序列分离、单通道观测条件下的单信号符号序列分离。综合前述，可知此四类子问题分别关注单通道条件下混叠观测中包含的多个目标信号时域波形的分离、某一特定目标信号时域波形的分离、多个目标信号符号序列的直接分离及某一特定目标信号符号序列的直接分离。

为了满足不同SCBSS 问题场景下的需求，本文在接下来的内容中主要对这四类问题进行了深入的分析和总结，以期为后续研究提供有益参考。

2.2 SCBSS 技术研究进展

本节将分别介绍不同分离任务的现有SCBSS算法，并分析现有研究存在的不足。具体将围绕以下四类分离任务展开：多信号波形分离、单信号波形分离、多信号符号序列分离、单信号符号序列分离，并重点关注针对通信信号的SCBSS 研究现状。SCBSS 任务及其技术研究情况如图4 所示。

图4 SCBSS 任务及其技术研究情况

2.2.1多信号波形分离

如2.1 节所述，多信号波形分离的任务是对混叠观测中包含的多个目标信号时域波形进行分离。由于多信号波形分离可以解决大部分BSS 应用场景下的问题，因此是SCBSS 中研究较多的一类分离任务。目前，已经有两大类SCBSS 算法完成了该分离任务，分别为基于伪多通道观测构建的算法和基于参数估计与波形重构的算法。

1) 基于伪多通道观测构建的算法

相对于SCBSS，多通道BSS 算法已经较为成熟，尤其是超/正定BSS 的研究。因此，解决SCBSS问题的一种重要思路是通过某种方式构建伪多通道观测，然后利用成熟的多通道BSS 算法实现多信号波形分离。

由于相对SCBSS 而言，关于多通道BSS 尤其是超/正定BSS 的研究已经较成熟，故解决SCBSS问题的一类重要思路是首先通过某种途径基于单通道混叠观测构建伪多通道观测，随后借助成熟的多通道BSS 算法实现多信号波形分离。

针对时频混叠数字通信信号的多信号波形分离，文献[21]提出了一种将奇异值分解（SVD,singular value decomposition）技术与独立分量分析（ICA,independent component analysis）技术结合的方法。其基本思路是通过时延和SVD 将单通道混叠观测转换为伪多通道观测，然后迭代地使用ICA对伪多通道观测矩阵进行处理，最后通过频谱分析和组合得到多信号波形分离结果。然而，该方法存在一些不足之处。首先，对多次ICA 分离结果的组合依赖人工分析，尤其是在各数字通信信号频谱混叠较严重时，对分离结果中分属于不同信号的分量较难区分，容易产生虚假信号。其次，多次ICA 过程及必需的后期处理使算法整体较烦琐，且分离结果可靠性降低。文献[22]提出了一种逐次提取的方式来分离多个数字通信信号波形。对于每个目标信号，首先，有针对性地设计时延参数，并基于时延将单通道混叠观测转换为伪多通道观测；然后，基于ICA 对伪多通道观测进行分离，并对存在冗余的分离结果进行波形及频谱的人工分析，确定属于同一目标信号的成分，将其组合得到该目标信号波形分离结果。然而，该方法对各目标信号载频差异度要求较高，且对分离结果的分析及后期处理要求较多的人工干预，分离可靠性不高。此外，其逐次提取各目标信号的过程较烦琐，需多次运用ICA 算法。文献[23]提出了一种基于连续小波变换（CWT,continuous wavelet transform）实现伪多通道观测构建的方法，利用ICA对伪多通道观测中的分量进行分离，通过频谱能量门限筛选从ICA 分离结果中确定与目标信号相关的部分，作为多信号波形分离结果。然而，该方法的不足在于ICA 分离得到的分量数多于实际目标信号数，需要经过后期筛选，筛选门限的确定主观性较强，从而导致其分离结果可靠性降低。

针对具有恒模特性的时频混叠数字通信信号波形分离，文献[24]提出了一种基于集合经验模态分解（EEMD,ensemble empirical mode decomposition）将单通道混叠观测分解为初始伪多通道观测的方法，并通过主成分分析（PCA,principal component analysis）对初始伪多通道观测进行降维，随后通过多次ICA 对降维后的伪多通道观测进行分离，每次均基于目标信号恒模特性提取分离分量中能量最大的部分作为某一目标信号的波形分离结果。然而，该方法分离过程较烦琐，且仅适用于具有恒模特性的数字通信信号。为应对信号分量存在能量差异的混叠信号，文献[25]通过人工设置谱相关系数和中心频率双重门限的方式来添加约束，提出了一种改进的EEMD 方法。

文献[26]在建立伪多通道观测时，初步尝试了贴合目标信号特性的方法。该方法基于数字通信信号的自回归（AR,autoregressive）特性，提出了时域阵列（TA,temporal array）的概念，实现了仅基于时延的伪多通道观测构建。随后，利用各目标信号间统计独立的特点，直接采用经典ICA 算法实现多信号波形分离。然而，该算法建立TA 的前提是混叠观测中各目标信号的载频不能相同。若混叠观测中存在载频相同的情况，该算法的分离性能会显著下降，甚至失效。此外，构建TA 的时延矢量对结果影响较大，需要根据测试数据进行人工确定。

从上述总结分析中可以看出，基于伪多通道观测构建的多信号波形分离算法存在2 个关键问题：如何构建伪多通道观测以及如何基于多通道BSS算法分离结果获取目标信号波形。然而，现有面向时频混叠数字通信信号的该类算法在这两方面存在不足。

首先，在伪多通道观测的构建过程中，现有算法对数字通信信号特性的挖掘与利用尚不充分，更多地依赖于通用数学工具，如SVD、CWT、EEMD等，导致构建过程的物理可解释性不强且效率较低。因此，构建的伪多通道观测未能很好地拟合实际多通道观测，从而导致一般无法基于多通道BSS算法直接实现多信号波形分离。

其次，在通过多通道BSS 算法对伪多通道观测进行分离后，分离结果往往存在冗余，需要依靠额外的人工分析与后期处理才能获取目标信号波形，使整个分离过程较烦琐且分离结果可靠性降低。对于多个目标信号波形的分离，一般需要多次运用多通道BSS 算法，从而降低了分离效率。

2) 基于参数估计与波形重构的算法

对于可以基于参数化模型进行精确建模的目标信号，若能获取其模型参数，则理论上可以直接对其信号波形进行重构。实现多信号波形分离的关键在于预先建立目标信号的准确参数化模型。对于通信信号，由于其具备明确的数学表达形式，因此基于参数估计的波形重构为时频混叠通信信号的多信号波形分离提供了另一有效思路。

文献[27]针对幅度时变及相位连续的通信信号，提出利用三阶多项式对目标信号瞬时相位进行拟合，将多信号波形分离问题转化为多个相位序列与信道参数的联合估计问题，并基于逐留存路径处理（PSP,per-survivor processing）技术进行求解，最后利用相位与信道参数的估计值对各个信号进行重构，实现多信号波形分离。针对窄带或慢变化目标信号，文献[28]提出在短时间内将其建模为单频信号，并利用能量算子及差分能量算子对其瞬时频率及瞬时幅度进行估计，并最终重构各目标信号。文献[29]提出了基于时变系数自回归模型对瞬时频率变化的非平稳信号进行建模，并假设该模型时变系数可由已知基函数加权获取，利用递归的方法对该系数进行估计，并最终对多目标信号波形进行重构。但上述算法主要适用于对模拟通信信号的分离，其对于数字通信信号尚不具备适用性。文献[30]提出了一种基于数据辅助信道估计的PSP 方法，通过将长序列分割成多个片段，选择检测可靠性最高的片段拼接在一起，有效应对了采样频率偏移不相同导致的时间滑移和符号滑移问题。

文献[31]利用时分多址（TDMA,time division multiple access）移动通信系统中参与混叠的数字通信信号具有显著功率差异的特点，提出首先对较大功率信号进行解调及波形重构，随后从混叠观测中抵消该重构信号而获取较小功率信号波形。该算法在各目标信号功率较接近时，性能将明显恶化，因而适用的场景较有限。

2.2.2单信号波形分离

单信号波形分离的任务是从混叠观测中分离得到某一特定目标信号时域波形。此时，除该目标信号外，其余参与混叠的信号均可被视为干扰。在通信抗干扰、特定信号检测等应用中，进行单信号波形分离对于高效获取目标信号、提升分离质量均具有重要意义。现有基于单通道观测实现单信号波形分离的算法主要包括基于广义谱维纳滤波的算法与基于信号子空间投影的算法。

1) 基于广义谱维纳滤波的算法

为了解决传统时/频域滤波对于时频混叠信号的失效问题，Hopgood 等[32]提出了广义谱域的概念。该概念假设存在某一谱域，使各信号在其中不存在混叠。在将混叠观测转换至该谱域后，可基于线性维纳滤波分离目标信号。Gardner[33]在该思路的基础上，假设各信号在循环频域内不存在混叠，利用数字通信信号循环平稳特性，提出了一种线性共轭-线性频移（LCL-FRESH,linear-conjugate-linear frequency shift）滤波器（简称FRESH 滤波器），成功实现了多个时频混叠数字通信信号中特定目标信号的分离。其基本原理是通过对混叠观测的不同频移分量的滤波结果进行加权求和，在增强目标信号的频移分量成分的同时减弱干扰信号的频移分量成分。以目标信号为QPSK 信号的情况为例，设其循环频率族为ψ={θ1,θ2,…,θr,θr+1,θr+2,…,θl}（前r个循环频率为非共轭循环频率，后l-r个循环频率为共轭循环频率），则将混叠观测输入FRESH 滤波器进行单信号波形分离的过程为

FRESH 滤波器的主要不足在于其对目标信号的先验信息要求较高。具体而言，其要求目标信号循环频率族已知且与干扰信号循环频率族不存在重合，同时需要获取目标信号波形本身作为训练信号以对各支路线性时不变滤波器系数进行优化调整。这在很大程度上限制了其实用性，尤其是在非合作通信场景下。为了降低FRESH 滤波器对训练信号的要求，文献[34]提出了一种盲自适应FRESH（BA-FRESH,blind adaptive FRESH）滤波器，直接以混叠观测的某一频移分量取代目标信号本身作为训练信号，因此相较 FRESH 滤波器而言，BA-FRESH 滤波器实用性显著提升。然而，BA-FRESH 滤波器仍要求对目标信号循环频率族的精确先验知识，其性能在循环频率存在误差时将显著下降[33]。同时，BA-FRESH 滤波器在分离性能上较标准的FRESH 滤波器存在一定的差距。

2) 基于信号子空间投影的算法

除了上述基于广义谱维纳滤波的算法外，还有一种重要的单信号波形分离技术思路，即信号子空间投影。其基本原理是首先基于已有的数学变换或基底学习过程构建子空间基底集，使目标信号与干扰信号在该基底集张成的子空间内尽可能正交；然后，通过将混叠观测投影到该信号子空间，实现单信号波形分离。

针对通信中抗同信道干扰的问题，文献[35]基于目标信号符号速率信息，确定合适的小波基底，使其张成目标信号在小波域内的零空间；然后，将混叠观测投影到该小波基底上，并基于干扰信号脉冲成形函数先验信息获取干扰信号估计；最后，通过将干扰信号估计结果从混叠观测中抵消，实现目标信号波形分离。需要注意的是，该方法要求目标信号为基带信号，且目标信号与干扰信号符号速率差异极小，对一般的时频混叠数字通信信号适用性不强。针对雷达信号处理中存在的非平稳信号分离问题，文献[36]提出了一种基于压缩感知的单信号波形分离算法。该算法假设目标信号可以由傅里叶基底稀疏表示，在通过短时傅里叶变换（STFT,short time Fourier transform）将混叠观测投影至时频域后，利用目标信号与干扰信号在时频域内的正交性及时频谱分析技术将其中包含干扰信号能量的时频点移除，并最终基于压缩感知对目标信号波形进行分离。需要注意的是，该方法要求目标信号与干扰信号在时频域内具有较高的正交性，这对于时频混叠较严重的数字通信信号而言难以成立。

除了上述基于已有通用数学变换的基底构建方式，还可以通过基于训练数据的学习过程构建更具有针对性的基底集。例如，在语音信号分离中，文献[37-39]提出首先以纯净目标信号为训练样本学习“字典”（即基底集），并保证目标信号可在该基底集张成的子空间内得到稀疏表示；然后，通过将混叠观测在所学得的基底集上进行稀疏编码（SC,sparse coding），即投影在基底集张成的子空间，实现目标信号波形分离。然而，现有基于训练数据进行基底学习的方法主要存在以下不足：1) 其要求以纯净目标信号作为构建基底的先验，这在常见的SCBSS 应用场景下难以得到满足；2) 传统的字典学习算法（如文献[37]中采用的K-SVD 算法[40]、贪婪自适应字典学习算法[41]和并行码字优化算法[42]）均需要基于对大量训练样本的迭代优化，一般而言计算量较大，例如，K-SVD算法需要对全局误差矩阵进行ηK次SVD 运算，其中，η为字典更新迭代次数，K为字典总原子数；3) 现有算法主要面向语音信号分离，尚不能较好地适用于数字通信信号单信号波形分离任务，尤其是如何利用数字通信信号的特性提升分离质量和分离效率仍然是值得深入研究的问题。文献[43]提出了一种基于稀疏编码和模板匹配的单信号波形分离算法。该算法假设混叠观测中存在目标信号单信号区域（SSR,single signal region)，首先，基于数字通信信号符号集的有限性，利用SC 实现目标信号SSR 检测；然后，直接以SSR 检测结果为模板构建目标信号子空间基底，通过模板匹配过程实现混叠观测非 SSR 部分的目标信号子空间投影，从而完成目标信号波形分离。该算法不依赖纯净目标信号波形的先验信息。但是，由人工参数设置的限制，该算法难以应对干扰信号强度较大、环境噪声水平变化等场景。文献[44]则基于数字通信信号的AR 特性，提出了一种基于字典学习及约束条件下稀疏编码的单信号波形分离算法。该算法同样假设混叠观测中存在目标信号的SSR，通过伪多通道观测构建和基于信息论准则的信号个数估计实现SSR 检测；然后，以SSR 检测结果为训练样本，利用经典DL 技术构建目标信号子空间基底；最后，通过在传统SC 中加入目标信号特性约束项的CSC 过程实现混叠观测非SSR 部分的目标信号子空间投影，从而完成目标信号波形分离。该算法同样不需要纯净目标信号波形的先验信息，同时人工参数明显减少。但是，当混叠信号中不存在SSR 时，这2 种算法的性能会急剧下降，且二者的处理过程较烦琐。

综合以上分析可以看出，现有实现单信号波形分离的SCBSS 算法主要存在以下不足。

首先，现有算法对目标信号的先验信息依赖较强，例如，FRESH 滤波器中对目标信号循环频率甚至信号波形的先验要求，以及基于字典学习与SC 的算法中对纯净目标信号训练样本的要求。在实际应用中，这些先验信息难以得到充分满足，尤其是在非合作通信条件下，这限制了现有算法的实用性。

其次，现有算法中基于字典学习构建基底集的过程计算复杂度较高，需要研究更高效的基底集构建方式。

最后，现有算法尚未充分挖掘发挥目标信号特性在单信号波形分离中的作用，需要针对数字通信信号开发更具有针对性、更高效的分离算法。

2.2.3多信号符号序列分离

多信号符号序列分离的任务是对混叠观测中包含的多个目标信号符号序列进行直接估计。这种任务通常出现在数字通信信号的分离中。当前完成这一分离任务的主流思路是对多信号参数、信道参数及符号序列进行联合估计，具体采用的技术主要包括粒子滤波（PF,particle filtering）与PSP。

粒子滤波是指通过确定一组在状态空间中传播的随机样本来近似地表示概率密度函数p(xn|zn)，其中，xn为系统在n时刻的状态，zn为n时刻的观测，通过计算样本均值来代替积分运算，进而获得对系统状态的最小方差估计的过程，这些随机样本被形象地称为“粒子”[45]。其具体数学过程如下。对于一个平稳随机过程，设n-1时刻系统的后验概率密度为p(xn-1|zn-1)，在n时刻可对选取的k个粒子进行观测及状态更新，并假设更新后k个粒子的后验概率密度为p(xn|zn)。随着粒子数目的增加，粒子的后验概率密度将逐渐趋近系统状态的真实概率密度，PF将可达到最优贝叶斯估计的效果[46]。针对符号速率相同的两数字通信信号的符号序列估计问题，文献[47]引入PF 技术，首先对单通道混叠观测进行符号速率采样，将两目标信号符号序列与信道参数等作为状态变量进行联合建模；经过粒子重要性采样及权值更新，对状态变量后验概率分布进行估计，以符号序列后验概率分布期望为多信号符号序列估计结果。文献[48]进一步对文献[47]算法在数学上进行了完善，使粒子重要性采样及权值更新的公式更完备准确。但早期基于PF 的多信号符号序列估计方法受限于各目标信号符号速率相同的场景。针对符号速率不同的两数字通信信号符号序列估计问题，文献[49]对单通道混叠观测的建模进行调整优化，给出了新模型下的状态空间转移方程，并推导了信号符号速率不同条件下的重要性采样及权值更新公式，实现了各目标信号符号速率不同场景下的多信号符号序列估计。除此之外，为解决基本PF 中难以避免的粒子数匮乏问题，研究者还提出了诸多改进PF 算法[50-52]，以进行更高质量的重采样。

但实际应用中，由于需基于大量粒子才能实现对系统状态后验概率密度的良好近似，故PF 主要受限于其极高的计算复杂度。为建立更高效、更具实用性的问题解决框架，文献[53]针对符号速率相同的两四相相移键控（QPSK,quadrature phase shift keying）信号的符号序列估计问题，首次提出了基于PSP 的解决方案。该方法仍基于目标信号符号序列与信道参数联合估计的思路，主要包括基于最小均方（LMS,least mean square）准则的参数更新及判决反馈。基于PSP 算法的多信号符号序列估计技术提出后引发广泛关注，研究者在文献[53]基础上提出了一系列改进算法。例如，为降低截断信道冲激响应对PSP 算法性能的影响，文献[54]提出基于Viterbi 检测获取预判决，并以其为基础合成信道冲激响应尾部造成的符号串扰。针对两高斯最小频移键控（GMSK,Gaussian minimum shift keying）信号的符号序列估计问题，Wu 等[20]提出将目标信号特性约束项引入传统LMS 算法中，有效提升了PSP 算法收敛速度及符号序列估计质量。文献[55]在基本PSP 算法基础上，分析了采用“判决-反馈”序列估计技术对符号序列估计性能的影响，并通过优化采样时刻提升了基本PSP 算法性能。文献[56]在原有PSP 算法的基础上，通过跟踪或估计载波残余带来的相位变化，提升了其在存在载波残余条件下的性能。在此，将两目标信号混叠场景下的基本PSP 算法步骤归纳如下[53]。

步骤1将经符号速率采样的单通道混叠观测建模为

步骤5在步骤3 和步骤4 经过充分迭代后（一般是符号序列候选路径已延伸至观测结束时刻），最终选择总体最优的符号序列候选路径，作为目标信号符号序列估计结果。

从式(5)可以看出，PSP 算法采用联合估计的方式对多个目标信号符号序列进行估计，即各目标信号符号序列的估计是相互耦合且相互影响的。在度量各符号序列延伸分支时，PSP 算法基于所有目标信号下一可能符号的组合来进行，这个组合数等于所有目标信号可能符号数的乘积，即调制阶数的乘积。这意味着，在每一步更新中，需要考虑的分支数与目标信号数及目标信号调制阶数都有关，而且随着它们的增加呈指数级增长。因此，尽管PSP 算法相对于PF 算法来说计算得到简化，但在目标信号数较多或调制阶数较高的情况下，PSP 算法的计算复杂度仍然很高。另一方面，现有的PSP 算法只能应对各目标信号符号速率相同的场景，对于各目标信号符号速率不同的多信号符号序列估计问题，PSP 算法尚不能有效解决，这极大地限制了其实用性。

除了基于PF 及PSP 的算法外，还有一些基于数字通信信号特性或其他先验信息的多信号符号序列估计算法，适用于目标信号被限定为（准）基带信号的特殊场景。例如，文献[57]通过对混叠观测进行过采样并矩阵化，利用目标信号脉冲成形函数先验信息，提出了直接通过矩阵求逆的方式求解各目标信号符号序列的方法。文献[58]针对目标信号为二元基带信号的特殊场景，提出了基于非监督聚类及目标信号二元取值特性的混叠系数估计方法，并基于混叠系数估计结果利用LMS 算法对多信号符号序列进行估计。文献[59]针对具备有限字符特性的基带信号，首先基于混叠观测差分直方图进行混叠系数估计，然后以最小重构误差为准则对目标信号可能符号组合进行遍历搜索，实现多信号符号序列估计。需要注意的是，上述算法仅适用于基带通信信号，对于一般时频混叠数字通信信号的适用性有限。

综上所述，现有单通道观测条件下的多信号符号序列估计算法主要在以下方面存在不足。

1) 现有主流基于模型的多信号符号序列估计算法（PF、PSP）均采用多信号符号序列联合估计的思路。这一思路决定其计算复杂度将随目标信号数及调制阶数的增长呈指数级增长，在参与混叠目标信号数较多或目标信号调制阶数较高的场景下，其算法实用性将因较低的计算效率而受到限制，尤其是基于PF 的多信号符号序列估计算法将因极高的计算复杂度而难以适用。

2) 现有基于PSP 的多信号符号序列估计算法在对目标信号参数的适应能力方面存在不足，主要是不能应对各目标信号符号速率不同的场景，导致其实用性受限。

2.2.4单信号符号序列分离

单信号符号序列分离是基于混叠观测对其中包含的某一特定数字通信信号的符号序列进行估计的过程。与单信号波形分离类似，这一分离任务主要出现在通信抗干扰等应用场合。如前文所述，现有进行目标信号符号序列估计的单通道BSS 算法多采用联合估计的方式，即耦合的同时估计多个目标信号符号序列，尚没有单独对某一特定目标信号符号序列进行估计的传统模型算法。对此类算法的研究对于高效、高质量地获取某一受干扰目标信号符号序列具有重要意义。

3 人工智能与SCBSS

本文第2 节中所述算法都是基于对目标信号、信道等先验信息建立的数学模型，因此属于基于模型的方法。与之不同的是，深度学习是一种数据驱动技术，依靠的是深度神经网络对输入/输出端数据间的复杂映射关系的强大建模能力，而不是基于先验信息建立数学模型。DNN 作为一种以数据驱动为主的网络结构，由输入层、多个隐藏层和输出层等组成，通过隐藏层的特征学习实现输入和输出的实时转换。目前，研究者已经开发了许多 DNN 架构，包括卷积神经网络（CNN,convolutional neural network）[60]、循环神经网络（RNN,recurrent neural network）[61]、自注意力（SA,self-attention）网络[62]等。

对于SCBSS 技术而言，DL 提供了一种离线训练的模型优化模式，以代替传统的在线更新优化模式。这种新颖的方法利用网络训练的方式学习输入信号到信号高质量恢复结果的精确映射。网络输入数据可以是直接接收的混叠信号波形数据，也可以是经过后处理提取的信号特征序列。目前，基于数据驱动的SCBSS 可分为2 种，一种是基于数据驱动的SCBSS，另一种是模型驱动和数据驱动相结合的SCBSS。

3.1 基于数据驱动的SCBSS

完全基于数据驱动的SCBSS 旨在特定域（时域、频域、时频域等）内实现混叠信号中期望信号的端到端分离。分离后的信号形式可以是波形序列，也可以是解调后的符号序列。该方法的优点在于它可以自适应地学习信号的特征，从而提高分离效果。

针对多信号波形分离问题，目前基于数据驱动的SCBSS 大多采用“编码器-分离器-解码器”的分离架构，其处理思路与传统基于伪多通道观测建构的算法相似。首先，通过一个浅层编码器网络将单通道混叠观测变换至高维表示；然后，分离器利用深层网路建模该高维表示获取各个期望信号的表示，并完成期望信号在高维空间的分离；最后，通过解码器将高维表示变换回时域，实现时域上端到端的多波形分离。例如，文献[63]首次将全卷积时域语音分离网络（Conv-TasNet,full convolutional time-domain audio separation network）[64]和双路径循环神经网络（DPRNN,dual-path recurrent neural network）[65]应用于SCBSS 领域，并提出了2 种SCBSS算法：基于Stacked-TCN 的SSCBSS 算法[66]和基于Stacked-LSTM 的SSCBSS 算法[67]。在不考虑频偏、相偏和定时偏差的情况下，这2 种SCBSS 算法均成功地完成了由BPSK、8PSK、16QAM、64QAM和PAM4 这5 种调制类型信号组成的10 种两两线性瞬时混合的混叠信号在时域上的端到端信号波形恢复任务。这初步验证了Conv-TasNet 和DPRNN在通信信号SCBSS 领域应用的适用性。文献[68]通过加深“编码器”以及添加通道注意力模块提出了一种改进的Conv-TasNet 方法，在BPSK 和QPSK两类调制信号混叠而成的数据集上取得了一定的性能增益。文献[69]提出了一种联合CNN 和双向长短期记忆（Bi-LSTM,bidirectional long short-term memory）网络的SCBSS 方法，能够有效地分离由雷达、通信及干扰信号三类信号组成的混叠观测。混叠观测中包括4 个信号，分别是2 个带宽不同的LFM 信号、一个BPSK 通信信号和一个SMSP 干扰信号，这些信号在时频域上具有明显的差别。该方法的提出为雷达和通信信号分离领域带来了新的思路和方法。文献[70]提出了一种基于注意力机制的端到端深度分离网络（ETEAMSN,end-to-end deep separation network based on the attention mechanism），该网络主要由带残差连接的注意力卷积单元组成。ETEAMSN 能够有效地分离由调制类型相同或者不同的期望信号组成的混叠信号，当信噪比（SNR,signal to noise ratio）为22 dB 时，成功地分离了BPSK/BPSK、QPSK/QPSK、BPSK/QPSK、BPSK/8PSK 和QPSK/8PSK 混合信号。但是，该网络无法有效地分离由高阶调制信号组成的混叠信号，如8QAM/8QAM 和8PSK/8PSK。随着信号调制阶数的增加，分离性能下降明显，而且分离性能容易受到期望信号之间的相对时延和相对能量比的影响。当时延相差较小或能量比相差较大时，分离性能下降明显。

针对多个同信道数字通信信号符号序列估计问题，文献[71]提出了一种基于CNN 的深度卷积网络解调器（DCND,deep convolutional network demodulator），其含两层CNN。在DCND 中，将单通道混叠观测直接输入CNN 中，以网络分类层输出作为多信号符号序列估计结果。该方法的不足之处在于，由于输入为原始混叠观测，未经过特征提取等预处理，因此在对某一目标信号符号序列进行估计时，仍将在相当程度上受到来自其他信号的干扰。这使该算法不能很好地应对各目标信号功率差异较显著的场景，因为功率较大的目标信号将对其余目标信号的符号序列估计带来较严重的干扰。

文献[72]针对PCMA 信号，提出了一种基于反向传播（BP,back propagation）神经网络的SCBSS方法。该方法首先构造包含不同比特信息的样本波形（3 个符号)；然后截取每个样本在末尾符号不同时的时频图；最后将时频图的特征数据作为输入数据，每个样本中前2 个比特序列作为训练的输出数据，网络对这些数据进行反复训练，直至完成分离模型的构建。在测试时，对PCMA 信号数据的时频图进行窗口截断，然后送入训练好的模型实现比特序列的恢复。该算法的复杂度比PSP 算法低，但损失了精度。

文献[73]针对两路QPSK 信号混叠的信号，提出了一种基于RNN 的SCBSS 分离网络。该网络包含两层RNN 层和一层全连接层，将符合序列检测视为分类任务，将混叠信号输入训练好的网络得到期望信号符号序列预测。与传统PSP 算法相比，该算法在计算复杂度降低的同时，取得了更好的性能，但其性能易受信号参数（时延差、相移差、采样率等）影响。

文献[74]将符号序列估计建模为序列标注问题，基于RNN 实现序列标注，构建了可进行多信号符号序列并行估计的单输入-多输出（SIMO,single-input multi-output）符号序列估计器。与DCND 直接以单通道混叠观测为输入不同，该方法首先基于单通道观测进行并行符号序列估计特征（FPSSE,feature for parallel symbol sequence estimation）提取，主要包括差分运算及特定时刻抽取，以获取分别包含各目标信号符号信息的特征序列。在对基于RNN 的符号序列估计器的离线训练及在线测试中，均以该特征序列为对各目标信号符号序列进行估计的网络输入。与现有基于模型的多信号符号序列估计算法不同，该方法采用的是多信号符号序列并行独立估计的思路，而非多信号符号序列联合估计，因此其计算复杂度不随目标信号数的增加而指数级增长。同时，其突破了PSP 算法对目标信号符号速率关系的限制，可以适用于各目标信号符号速率相同或不同的场景。此外，由于通过FPSSE 提取抑制了各目标信号相互间的干扰，在各目标信号功率差异较显著的情况下，估计性能较DCND 具有显著优势。但该方法存在以下不足：1) 各个期望信号的FPSSE 提取需要各个信号满足符号速率不同或者速率相同但存在相对时延；2) FPSSE 提取易受成形滤波器类型的影响，码间串扰的存在会使在没有符号速率、信号调制类型等先验信息下提取的FPSSE 表征能力下降，且随着期望信号数量的增多，码间干扰逐渐严重。

针对单信号符号序列估计问题，文献[75]从通信抗干扰的典型场景出发，主要关注对所提取特征中干扰信号成分的抑制，尤其是实际中常见的强窄带干扰信号。与文献[74]相似，其仍将符号序列估计建模为序列标注问题，并基于RNN 实现序列标注，构建了可进行特定目标信号符号序列估计的单输入-单输出（SISO,single-input single-output)符号序列估计器。该方法通过特定时刻抽取与差分运算，基于混叠观测提取了一种抗干扰符号序列估计特征（IRFSSE,interference-robust feature for symbol sequence estimation)，然后基于RNN 完成了典型的通信抗干扰场景下特定信号符号序列的估计任务。但该方法除了存在与文献[74]方法相似的缺陷外，还需要满足干扰信号存在时间远小于期望信号，仅考虑了窄带干扰信号的场景，方法普适性较差。

3.2 模型驱动和数据驱动相结合的SCBSS

与传统基于模型驱动的SCBSS 算法不同，另一种方法是将模型驱动和数据驱动相结合的SCBSS 方法。这种方法将SCBSS 模型中的矩阵求逆和参数优化等计算压力转移到数据驱动层面，利用数据驱动的计算效率高的优势，用其替代传统BSS 方法中计算复杂度高或优化难的处理模块，以此降低算法总体计算复杂度。同时，简化模型优化和参数选取过程，以提高算法整体性能。

文献[76]提出了一种基于 BP 神经网络的PCMA 信号盲分离模型，该方法利用预处理模块指导神经网络批处理梯度算法训练过程，进而联合神经网络分离模块与最优路径判决模块实现PCMA信号有效分离，相较于传统PSP 算法需遍历两路发送符号重构信号的过程，该算法仅需遍历一路发送符号用于重构信号，具有复杂度低的特点。文献[77]为解决传统PSP算法无法准确跟踪信道而导致的后续序列符号恢复效果差的问题，针对PCMA 信号，提出了一种基于RNN 的信道插值与估计算法。该算法利用最小二乘（LS,least square）算法计算出导频符号处的信道初始估计值；然后，将其送入RNN得到信道插值估计值；最后，通过最大似然序列估计（MLSE,maximum likelihood sequence estimation）信号分离算法得到两路信号的符号估计值。与传统信道插值估计方法相比，该方法在计算复杂度降低的同时，取得了更好的估计性能。

4 结束语

4.1 挑战与解决思路

综上所述，无论是基于数据驱动的SCBSS 技术，还是模型驱动与数据驱动相结合的SCBSS 技术，在改善信号恢复性能、提高计算效率、降低模型优化难度等问题上都具有显著的优势。然而，深度学习本身可解释性较差，其进行信号建模分析的逻辑类似于黑盒。再加上现有算法尚未充分挖掘发挥目标信号特性，对信号分离背后对应的机理问题并未完全解决。因此，尽管基于数据驱动的SCBSS方法在分离效果上有明显的优势，但是很容易陷入过拟合，面对新数据针对新情景的分离效果往往不尽如人意。这也限制了基于深度学习的SCBSS 方法向实际应用系统的转化。

针对此类问题，现阶段主要有3 种解决思路。

1) 深度学习联合传统基于模型的SCBSS，利用深度学习强大的数据表示能力，将其作为自适应模块替代传统方法中某些需要大量人工设置的环节，以提升算法性能。此时的神经网络结构属于浅层网络，具有清晰的数学计算可解释性。

2) 深度学习联合人工知识库，即利用专家知识去掉干扰信息，剥离出特定信号的知识规则，通过对学习过程添加知识规则约束，引导神经网络结构学习可解释的信号知识。

3) 深度学习联合信号特性，数字通信信号具有良好的数学建模逻辑，其特有的信号特性（如自回归特性、周期性、独立性、稀疏性等）可作为神经网络结构设计的依据，联合信号特性构建的网络结构具有清晰的计算逻辑，为网络学习过程提供机理支撑。

总体而言，数据驱动与模型驱动协同驱动的SCBSS 方案将更具实际应用价值。通过数据驱动技术挖掘数据含义，以数据打破模型局限，学习潜在规律，激发内生智慧；同时，结合模型驱动，克服数据困境，以模型补偿数据不足，定量刻画系统，促进分离性能提升。数据/模型联合驱动的处理示意如图5 所示。此外，与以往的端对端方法相比，结合信号特性来提高基于深度学习的SCBSS 系统性能的思路对信号分析和机理理解都提出了更高的要求。

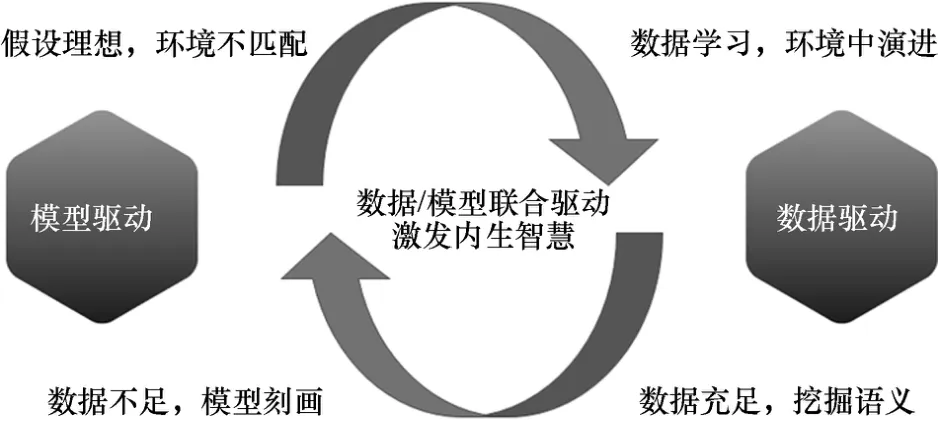
图5 数据/模型联合驱动处理示意

4.2 发展趋势分析

SCBSS 问题经过多年的研究，相关的技术应用逐步成熟。现阶段，传统的SCBSS 算法在很大程度上依赖于期望信号的部分或全部先验信息，且其涉及的信号种类、建模的分析角度、依据的理论知识也各不相同。然而，随着通信技术的发展，新体制信号层出不穷，用频设备数量爆炸式增长，接入设备的多样化，电磁环境将更加复杂，实现期望信号有效分离的难度越来越大。因此，今后SCBSS技术的相关方法，特别是信号的先验信息获取方法、新体制信号的建模方法和多源信号的联合建模方法，仍需要深入研究以下几个方面。

4.2.1智能SCBSS 模型

智能学习的方法能够在一定程度上摆脱对专家知识的依赖，改变传统的人工预定义处理流程，实现自动学习SCBSS 模型，从而提高分离方法的适应能力。利用DL 方法建模电磁信号中蕴含的数字通信信号特性信息，未来能在SCBSS 问题上发挥更大的作用。然而，目前基于数据驱动的SCBSS方法在智能化、自动化分离数字通信信号方面还处于尝试摸索阶段。特别是如何结合专家经验和数字通信信号本身的特性，更好地发挥智能计算的优势，真正实现稳定有效的分离模型学习等问题需要更加细致深入的研究。

4.2.2模型方法的综合利用

目前存在大量不同种类的模型，但单一模型的适用范围和表征能力有限，不同模型的关注点和侧重点也存在差异。因此，综合利用多种模型的方法可以从更多的角度刻画目标信号特性，为SCBSS问题提供更全面的信息。在SCBSS 领域中，模型的综合利用不仅包括模式识别中的多模型融合问题，更强调对信号的理解和认识，发挥不同种类SCBSS 模型对目标信号特性不同角度刻画能力的优势。这既避免了冗余，又防止了缺漏。针对SCBSS 问题，未来多模型综合利用的基本思路应该以提高SCBSS 模型对不同信号的适应能力、增强对特定信号的针对性、促进原有模型的优势互补为出发点。换句话说，今后SCBSS 的相关研究应该在定义和提取新模型的同时，提高对原有优异模型的利用。

4.2.3模型适应性和扩展性

目前，大部分模型只能适应有限的信号类型，而且其适用范围和条件并不明确。当出现新的信号形式时，通常需要结合专家知识进行模型的筛选和摸索，但面对新的场景，原有的识别效果往往会大打折扣，甚至失效。如今，电磁环境日益复杂，雷达通信乃至物联网设备信号的类型和样式不断增多，这考验着SCBSS 模型的适应性和扩展性。此外，SCBSS 模型的边界特性同样值得关注。随着SCBSS 技术的应用越来越广泛，对SCBSS 模型也提出了越来越高的要求。无论是依赖专家知识人工定义，还是基于数据驱动技术自动学习，未来的SCBSS 技术模型需要向更加精细化、智能化、复杂化和深层次的方向发展。