超埋深高应力复杂地层巷道围岩损伤分区与承载结构特征研究
2023-09-19雷显权刘福春严庆文张帅帅郭奇峰王勇兵汪小东
雷显权 刘福春 严庆文 张帅帅 郭奇峰 王勇兵 汪小东
(1.长沙有色冶金设计研究院有限公司,湖南 长沙 410019;2.深井矿山安全高效开采技术湖南省工程研究中心,湖南 长沙 410019;3.中南大学资源与安全工程学院,湖南 长沙 410083;4.云南驰宏锌锗股份有限公司会泽矿业分公司,云南 曲靖 654200;5.北京科技大学土木与资源工程学院,北京 100083)
随着浅部矿产资源的日益枯竭,我国矿产资源开发即将全面进入第二深度空间(1 000 ~2 000 m),深部资源开采逐渐成为矿产资源开发新常态[1-3]。进入深部开采后,地应力显著增大,地质环境复杂多变,矿岩非线性力学特征显著,开采扰动强烈,巷道变形、片帮、塌方、冒顶、岩爆等灾害问题突出,给深部巷道围岩稳定性控制与矿山生产安全防控造成巨大挑战[4-6]。为了应对深部高应力复杂环境条件下巷道失稳致灾问题,相关学者开展了大量研究,在深部开采岩体力学特性、围岩变形破坏机理、岩层稳定性控制方法、巷道支护技术和地压灾害监测预警等方面取得了长足进展[7-12]。
巷道围岩的损伤分区和承载结构特征是巷道稳定性评价的重要内容,也是巷道岩层控制与支护设计的重要依据。康红普[13-14]于1997 年首次提出巷道围岩关键承载圈概念,分析了围岩承载圈的分布特征及其影响因素,阐述了关键承载圈对巷道支护的工程意义。李树清等[15-16]采用弹塑性理论分析和数值模拟方法研究了巷道围岩的承载结构特征,分析了深部巷道与浅部巷道围岩承载结构的差别,探讨了支护阻力对深部巷道围岩承载结构的影响。赵光明等[17-18]通过理论分析和数值模拟,将软弱破碎巷道围岩的承载结构划分为浅支撑层、深支撑层和关键支撑层,分析了各支撑层对围岩变形的控制作用以及岩体残余强度和支护作用对围岩承载结构演化和巷道变形的影响。Qin 等[19]采用理论分析和数值模拟相结合的方法研究了动压作用下深部软岩巷道围岩的承载结构,分析了不同支护方式对围岩承载结构的控制效果。Zhang 等[20]采用理论分析、数值模拟和现场试验相结合的方法研究了巷道开挖空间效应产生的应力调整和重分布对围岩力学特性及承载结构的影响,揭示了岩石破裂发展状态对围岩承载结构的调节机制。王玺等[21]通过理论计算和数值模拟实验,研究了不同岩体质量等级巷道围岩的承载结构特征,分析了岩体质量等级对各承载区主应力分布和塑性破坏的影响。这些研究深化了对巷道围岩承载结构特征及其作用机理的认识,对巷道围岩稳定性控制与支护具有重要指导作用。
充分发挥围岩的自身强度和自承能力以达到采矿工程的稳定是矿山岩石力学最基本的原理[22-23]。为了实现这一目的,首先就要了解和掌握围岩的损伤分区和承载结构特征。虽然前人对巷道围岩承载结构相关问题进行了大量研究并取得了丰富成果,但由于深井矿山开采环境的复杂性,还存在许多问题需要作进一步研究和探讨,比如超埋深高应力复杂地层巷道围岩承载结构的差异性及稳定性问题。针对该问题,本研究以云南某深井开采矿山1 500 m 埋深中段石门巷道为例,采用弹塑性理论分析、松动圈现场测试和数值模拟计算相结合的方法,研究了超埋深高应力条件下不同地层巷道围岩的损伤分区和承载结构特征,分析了不同地层围岩损伤区和承载结构的差异及其原因,探讨了不同地层围岩承载结构与巷道稳定性的关系,提出了一种确定深部巷道锚杆支护长度的新方法,为该矿山深部巷道围岩稳定性控制与支护提供理论指导。
1 工程概况
云南某矿山是目前国内已建成投产的开采深度最深的矿山,最低开采中段埋深超过1 500 m。矿山地层、构造条件复杂,深部巷道埋深大、地应力高,开采扰动强烈,具有典型的“三高一扰动”特征。现场调查结果显示,在深部复杂环境条件下,巷道围岩变形、喷层开裂和支护破坏现象多见,发生片帮、冒顶和大规模失稳的安全风险突出,给巷道稳定性控制造成极大挑战。
以该矿山深部某中段石门巷道为研究对象(图1)。该中段埋深约1 500 m,巷道断面形状为三心拱形,断面规格为3.40 m×3.20 m。巷道从竖井马头门往SE 方向开拓掘进,依次穿越震旦系陡山沱组、灯影组、寒武系筇竹寺组,泥盆系宰格组,石炭系大塘组、摆佐组、威宁组、马坪组,二叠系梁山组、栖霞—茅口组等多组地层以及多条断层。
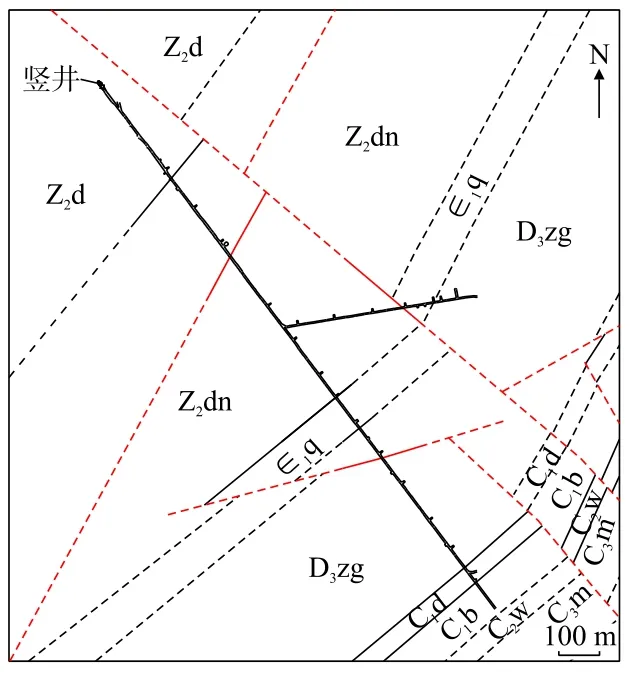
图1 研究区巷道布置Fig.1 Roadway layout in research area
根据巷道埋深和上覆岩层重度估算垂向应力约为42 MPa。矿山1 500 m 深处的地应力测量结果显示,最大主应力为42.34 ~45.95 MPa,平均43.78 MPa,最大主应力方向为NNW-SSE[24]。现场节理裂隙调查和岩体质量评价结果显示,巷道围岩的岩体质量等级以Ⅲ~Ⅳ级为主。通过室内基础岩石力学试验,获得了不同地层岩块试样的力学参数。以此为基础,结合岩体节理裂隙调查和岩体质量评价结果,采用等效Hoek-Brown 强度准则与Mohr-Coulomb 强度准则的岩体力学参数估算方法[25-26],获得了深部巷道围岩的岩体力学参数,见表1。

表1 深部岩体力学参数Table 1 Mechanical parameters of deep rock mass
2 深部巷道围岩损伤分区与承载结构模型
假设巷道围岩为均质各向同性连续介质,本构关系为弹塑性软化模型。基于圆形开挖断面和小孔扩张理论,建立如图2 所示的巷道围岩受力分析模型。巷道开挖后,围岩应力发生二次重分布,并产生应力集中,导致围岩发生不同程度的损伤破裂。根据围岩应力分布特征和损伤破裂程度,围岩变形损伤区由表及里依次划分为破碎区(或松动区)、塑性软化区、弹性区和原岩应力区[8,17-18]。其中,破碎区和塑性软化区为塑性变形区,即广义上的塑性区;弹性区和原岩应力区为弹性变形区。
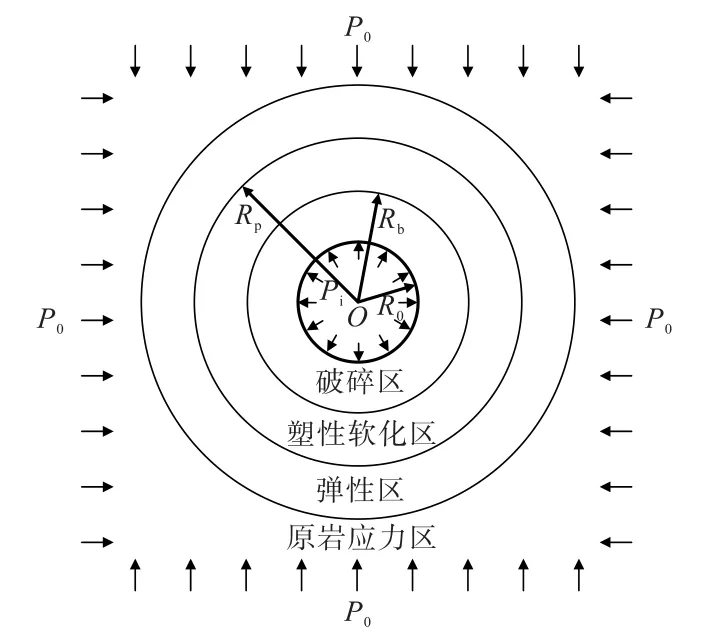
图2 巷道围岩受力分析模型Fig.2 Mechanical model of roadway surrounding rock
根据巷道开挖后围岩二次应力分布规律,并结合围岩变形损伤分区特征,建立如图3 所示的深部巷道围岩承载结构模型。将σθ>P0的区域定义为承载区。如图3(a)所示,破碎区(A-B)为应力降低区(σθ<P0);塑性软化区(B-C)虽然发生了塑性屈服,但仍具有较高的承载能力,将其划为塑性承载区;弹性区(C-D)强度几乎没有受到损伤弱化,承载能力很高,将其划为弹性承载区;在塑性承载区和弹性承载区范围内,存在一个相对高应力区(σθmax>σθ>kP0),是承受围岩压力的关键区域,将其划为关键承载区(EF)。研究表明,k值范围一般为1.2 ~1.5[17-18,21]。综合考虑计算得到的巷道围岩二次应力分布特征及其与最大峰值应力和原岩应力的关系,本研究k值取1.3。图3(b)显示了深部巷道围岩承载区与变形损伤区的对应关系。
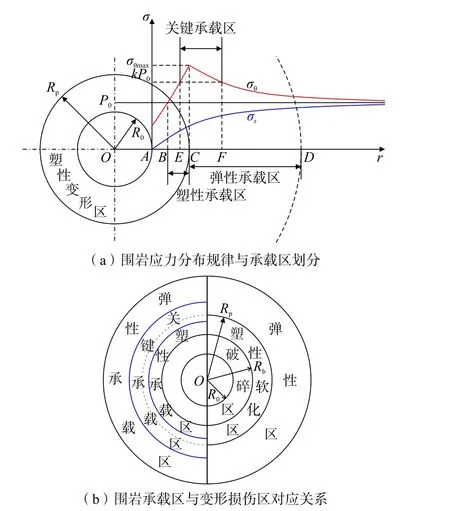
图3 深部巷道围岩承载结构模型Fig.3 Load-bearing structure model of deep roadway surrounding rock
3 深部巷道围岩损伤分区与承载结构特征
3.1 弹塑性理论计算塑性区深度
基于圆形巷道力学模型和Mohr-Coulomb 屈服准则,通过弹塑性力学理论分析,可求得巷道围岩塑性区半径Rp的计算公式,即卡斯特奈(H.Kastner)公式或修正芬纳(R.Fenner)公式[27]:
原岩应力可通过地应力实测获得,或采用下式进行估算:
式中,γ为岩体容重;H为巷道埋深。
当支护阻力Pi为0,即巷道开挖未支护时,围岩塑性区半径Rp计算公式为
为了便于计算,基于最小外接圆原则,采用几何作图法得到矿山深部三心拱形巷道的等价圆形断面,以获得巷道等效半径,即2.08 m。然后根据研究矿山深部巷道围岩的岩体力学参数(表1)及其所处的地应力环境(原岩应力P0取42 MPa),计算得到不同地层巷道围岩的塑性区深度,见表2。计算结果显示,不同地层围岩塑性区深度范围为1.62 ~3.03 m,平均2.16 m。
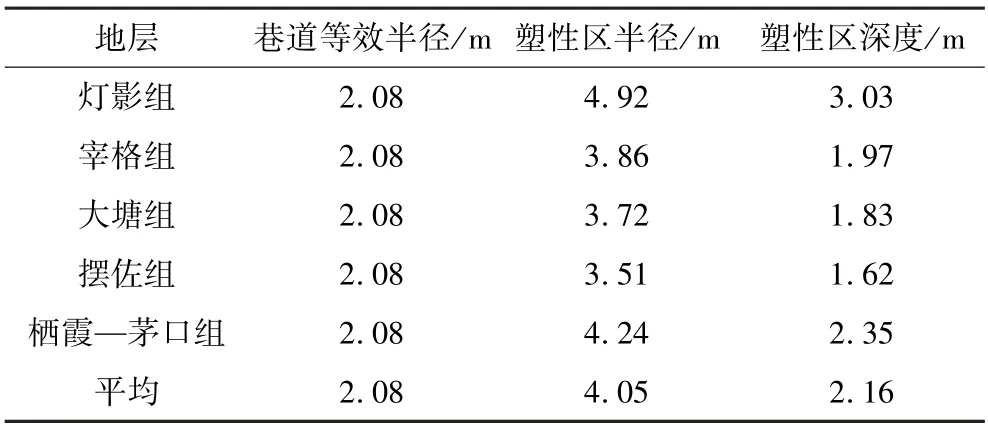
表2 不同地层围岩塑性区理论计算结果Table 2 Theoretical calculation results of plastic zone of surrounding rock in different strata
3.2 声波法现场测试松动圈深度
根据巷道围岩松动圈支护理论[28-29],巷道开挖后,原岩应力在围岩中发生重分布并产生应力集中,当集中应力超过围岩强度时,巷道周边围岩发生破坏,形成一条环向破裂带,该破裂带被称为围岩松动圈。松动圈的范围通常采用现场实测方法获得,作为巷道支护分类和参数设计的依据。
本研究采用声波法进行松动圈测试。声波在岩体中的传播速度与岩体的结构及其物理力学性质密切相关。在裂隙发育、低密度、高声阻抗岩体中,声波传播速度较慢;在高应力、高密度岩体中,声波传播速度较快。因此,通过测试超声波在巷道围岩钻孔内的传播速度,绘制波速—孔深曲线,分析波速沿孔深的变化规律,就可以判断围岩松动圈的范围。
现场测试采用武汉中科智创生产的RSM-SY5 型智能声波检测仪以及与之配套的一发双收探头。该检测仪具备自动判读功能,使得首波声时、声幅读取更为准确。测点布置在巷道侧壁,针对不同地层巷道围岩,共完成了11 个点的松动圈测试,结果见图4 和表3。实测结果显示,不同地层围岩松动圈深度范围为0.9~1.9 m,平均1.38 m。
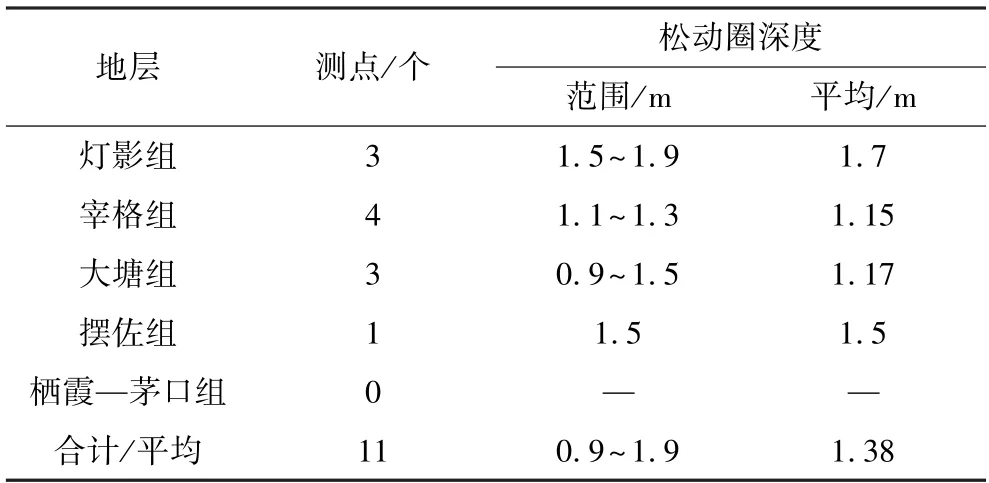
表3 不同地层围岩松动圈测试结果Table 3 Test results of rock loose circle in different strata

图4 松动圈测试波速—孔深曲线Fig.4 Wave velocity-hole depth curve of rock loose circle test
3.3 数值模拟分析塑性区特征
根据研究矿山深部巷道几何特征,采用FLAC3D软件,建立巷道开挖数值计算模型。采用8 节点六面体单元划分网格,为了提高计算精度,对巷道周边网格进行了加密,划分后的网格模型包括46 820 个单元和52 030 个节点。模型几何尺寸和网格划分情况如图5 所示。
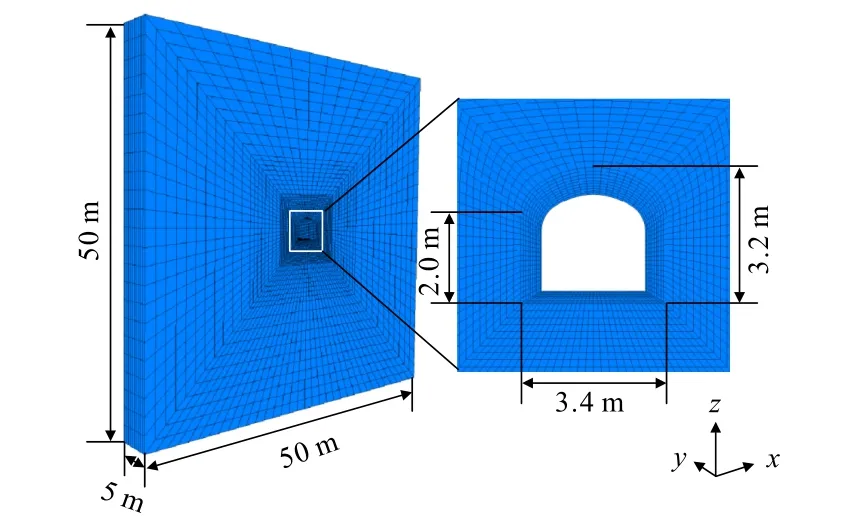
图5 巷道模型网格Fig.5 Mesh grid of roadway model
巷道围岩的变形破坏行为采用耦合张拉屈服准则的Mohr-Coulomb 强度准则来描述,屈服函数如下:
式中,σ1和σ3分别为最大和最小主应力;Fs和Ft分别为剪切和张拉屈服函数。
模型物理力学参数见表1。根据地应力实测和理论估算结果,并考虑巷道走向与最大主应力方向近似平行的关系,在模型x、y方向上分别施加42 MPa和43.78 MPa 的水平应力,在模型z方向上施加42 MPa 的垂向应力和9.8 m/s2的重力加速度。
采用FLAC3D软件计算模拟巷道开挖过程。根据数值模拟结果,绘制了不同地层巷道开挖后的围岩塑性区分布结果,见图6。在此基础上,根据上述深部巷道围岩损伤分区理论模型,获得了不同地层巷道围岩的损伤区(破碎区和塑性区)深度,见表4。数值模拟结果显示,不同地层围岩破碎区深度范围为0.92~1.63 m,平均1.20 m;不同地层围岩塑性区深度范围为1.48~2.50 m,平均1.87 m。
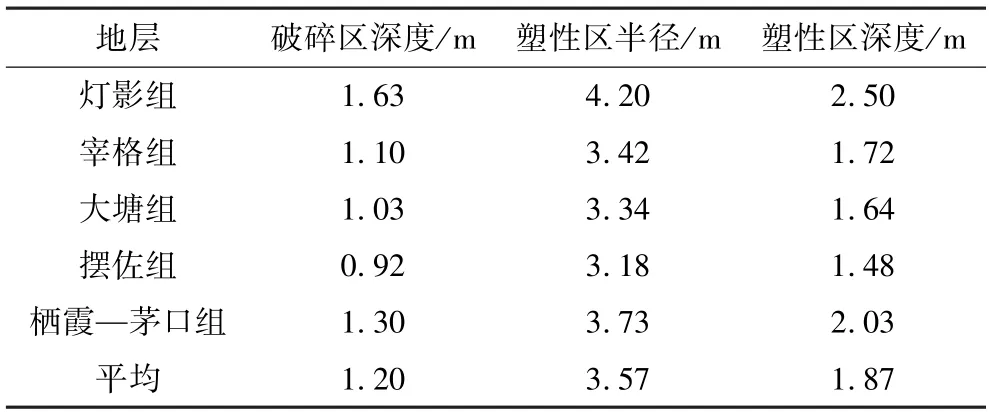
表4 不同地层围岩损伤区数值模拟结果Table 4 Numerical simulation results of damage zone of surrounding rock in different strata

图6 不同地层围岩塑性区分布特征Fig.6 Distribution characteristics of plastic zone of surrounding rock in different strata
3.4 深部巷道围岩承载结构划分
基于数值模拟得到的巷道围岩应力分布规律和损伤区分布结果,根据上述深部巷道围岩承载结构理论模型,划分了不同地层巷道围岩的承载区,见图7,并获得了不同承载区的结构参数,见表5。研究结果显示,巷道围岩塑性、弹性和关键承载区平均深度范围分别为1.20~1.88 m、1.88~8.09 m 和1.58~2.86 m,平均厚度分别为0.68 m、6.21 m 和1.28 m。
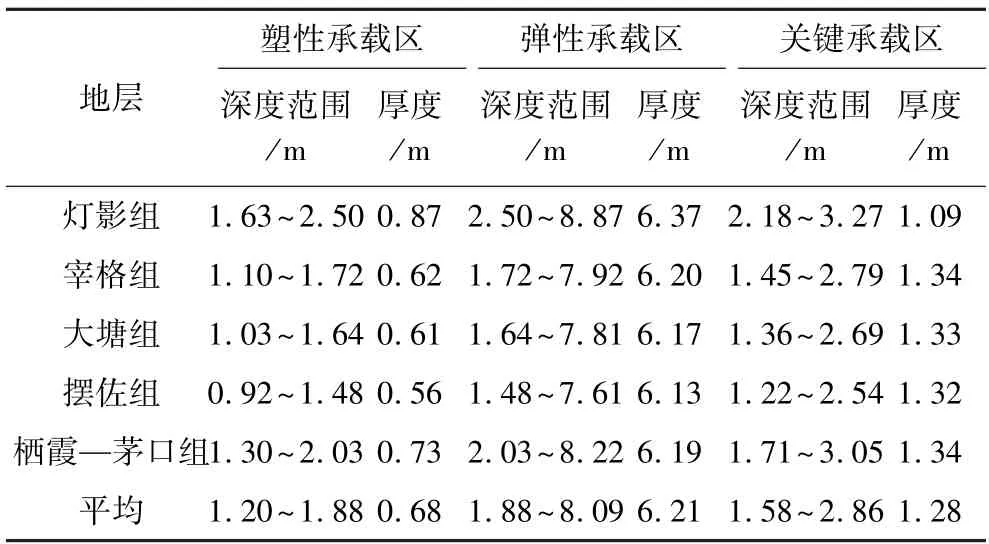
表5 不同地层围岩承载区划分结果Table 5 Results of load-bearing zone division of surrounding rock mass in different strata
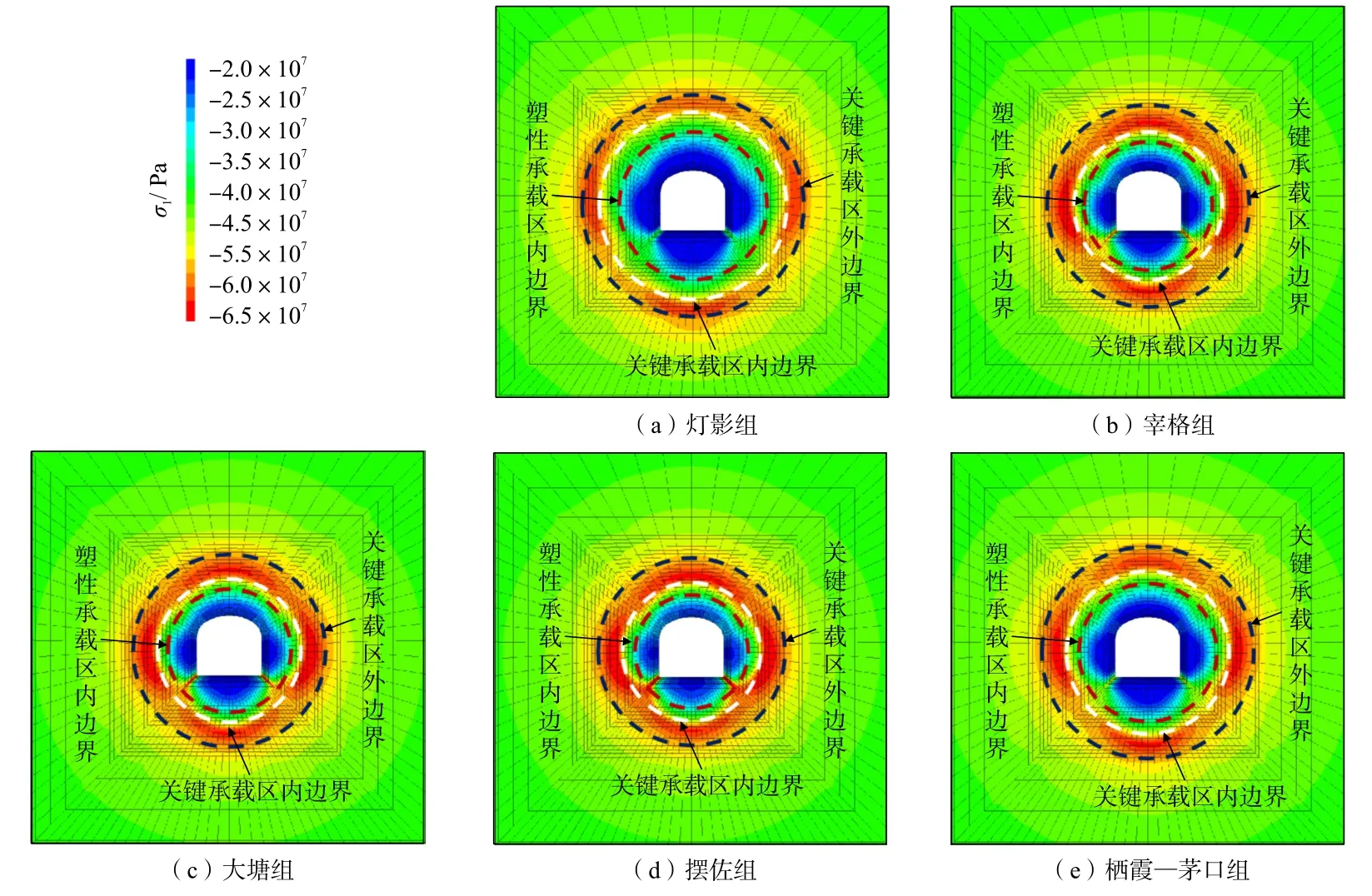
图7 不同地层巷道围岩最大主应力分布特征Fig.7 Distribution characteristics of maximum principal stress in surrounding rock of different strata
4 分析与讨论
4.1 不同围岩损伤区与承载结构的差异
4.1.1 不同地层围岩损伤区深度对比
图8 所示为采用上述3 种方法得到的不同地层巷道围岩损伤区深度对比。从图8 可以看出,不同地层围岩的损伤区深度存在明显差异,塑性区及破碎区深度由大到小排序为:灯影组>栖霞—茅口组>宰格组>大塘组>摆佐组。不同方法得到的损伤区深度虽有差异但变化趋势基本一致。由图8(a)可以看出,对于同一地层,围岩塑性区深度理论计算结果比数值模拟结果偏大,主要原因是理论计算没有考虑巷道围岩的三维结构。由图8(b)可以看出,对于同一地层围岩,灯影组、宰格组和大塘组的破碎区深度数值模拟结果略小于松动圈实测平均结果,但都在松动圈实测结果(表3)范围内;摆佐组破碎区深度数值模拟结果与松动圈实测结果相差较大,主要是因为摆佐组只进行了1 次松动圈实测,没有反映松动圈深度的统计特征。上述3 种方法研究结果的对比分析也表明,数值模拟方法能够较为客观准确地揭示深部巷道围岩的损伤破坏特征。
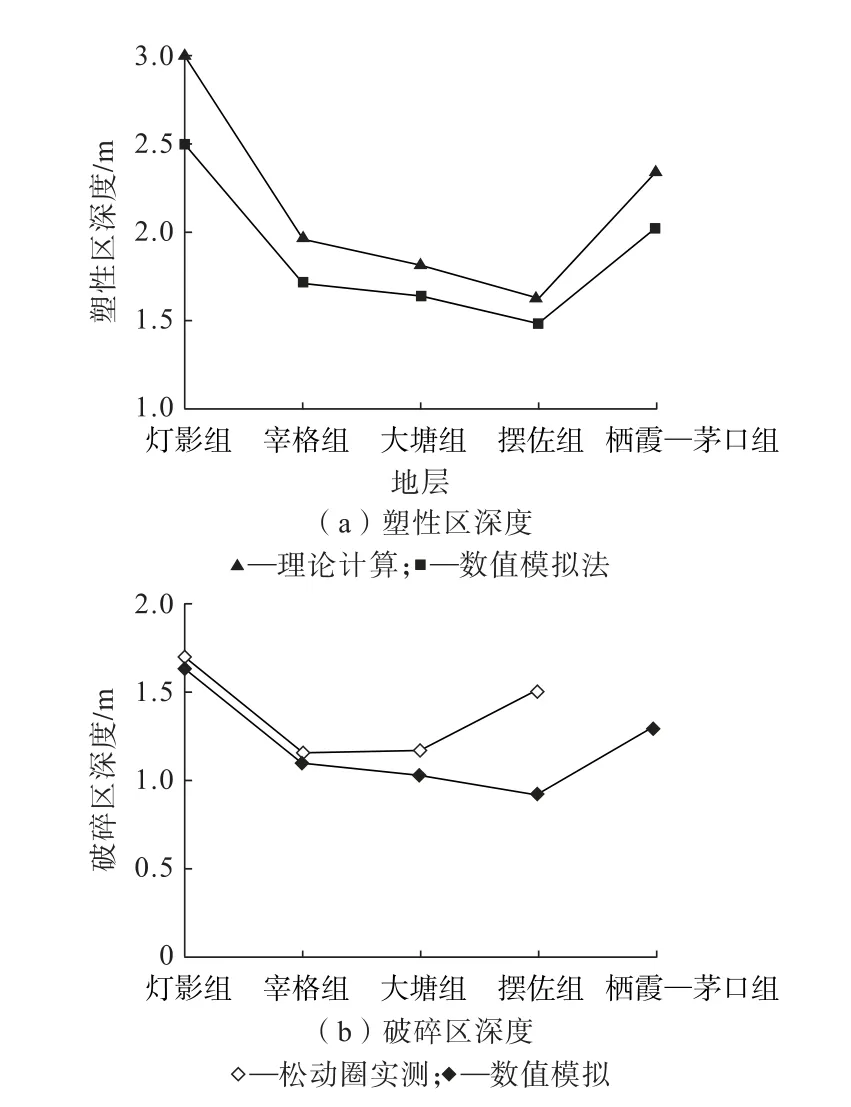
图8 不同地层围岩损伤区对比Fig.8 Comparision of damage zone of surrounding rock in different strata
图9 所示为巷道围岩损伤区深度与岩体强度的关系。由图9 可以看出,围岩塑性区、破碎区深度均与岩体抗压、抗拉强度呈负线性相关关系。总体而言,岩体抗压、抗拉强度越大,围岩损伤区深度越小。这表明,在相同的地应力条件下,巷道围岩的损伤破坏程度主要取决于岩体强度。虽然这一结论早已从理论上得到预测,但本研究进一步基于深井矿山高应力巷道实例并通过围岩松动圈现场实测和三维数值模拟实验验证了这个结论。
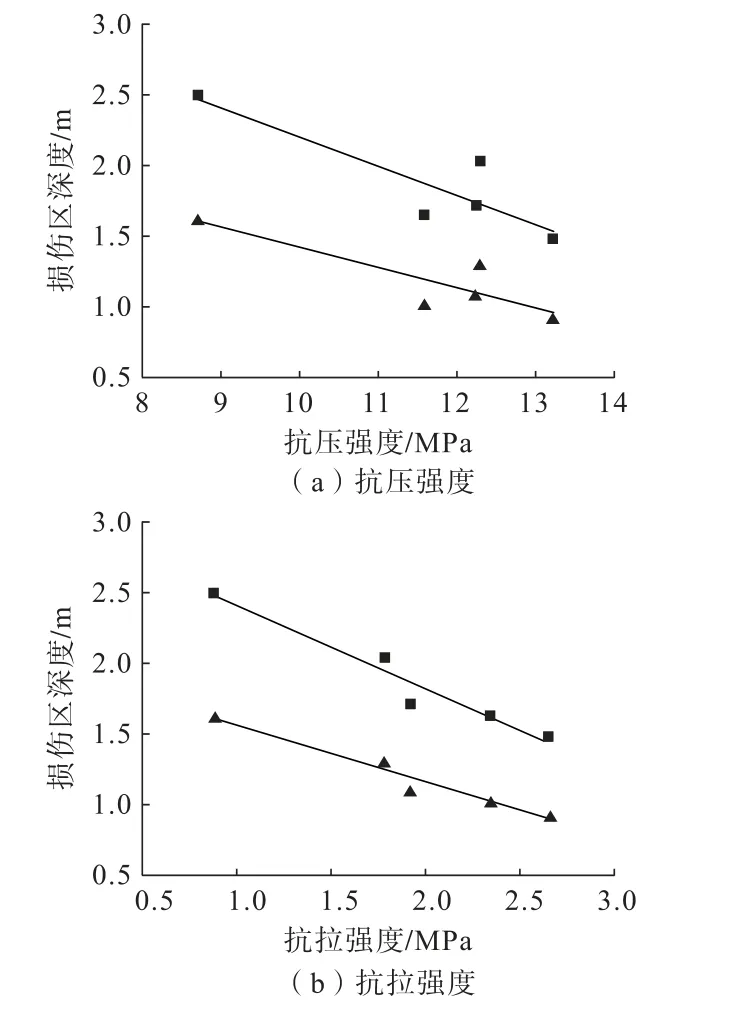
图9 围岩损伤区与岩体强度关系Fig.9 Relationship between damage zone and strength of surrounding rock
4.1.2 不同地层围岩承载结构对比
图10 所示为不同地层巷道围岩承载结构参数对比。由图10(a)可以看出,不同地层围岩的承载区厚度没有明显差异,除灯影组外,宰格组、大塘组、摆佐组和栖霞—茅口组围岩的塑性、弹性和关键承载区厚度均非常接近。由图10(b)可以看出,不同地层围岩的承载区深度存在显著差异,但塑性、弹性和关键承载区深度变化趋势一致,由大到小排序为:灯影组>栖霞—茅口组>宰格组>大塘组>摆佐组。这也与上述不同地层围岩损伤区深度排序相一致。

图10 不同地层围岩承载结构对比Fig.10 Comparison of load-bearing structures of surrounding rock in different strata
图11 所示为巷道围岩承载结构参数与岩体强度的关系。从图11 可以看出,围岩塑性、弹性和关键承载区深度均与岩体抗压、抗拉强度呈负线性相关关系。总体而言,岩体抗压、抗拉强度越大,围岩承载区深度越小。
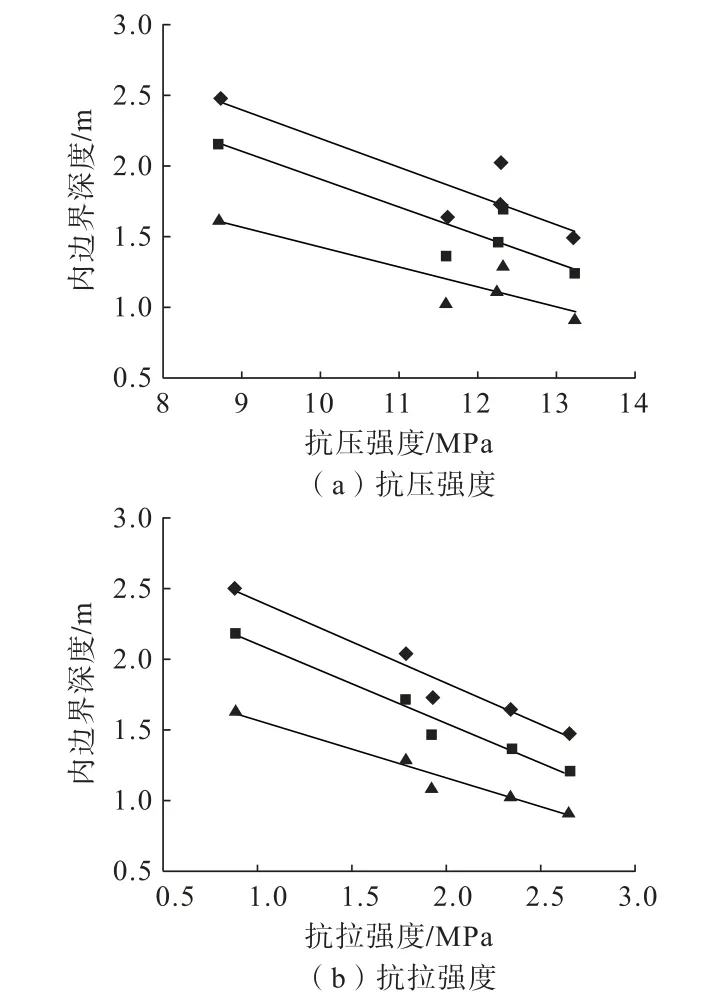
图11 围岩承载结构与岩体强度关系Fig.11 Relationship between load-bearing structures and strength of surrounding rock mass
4.2 围岩承载结构与巷道稳定性的关系
图12 所示为不同地层巷道开挖后围岩变形特征对比。从图12 可以看出,不同地层围岩的总体变形特征相似,但位移量存在明显差异,顶板、巷帮最大位移由大到小排序为灯影组>栖霞—茅口组>宰格组>大塘组>摆佐组。

图12 不同地层围岩变形特征对比Fig.12 Comparison of deformation characteristics of surrounding rock in different strata
图13 所示为巷道开挖后围岩位移、损伤区深度与关键承载区深度的关系。从图13 可以看出,顶板、巷帮位移量以及围岩塑性区、破碎区深度均与关键承载区深度呈正线性相关关系。总体而言,关键承载区深度越大,围岩位移量和损伤区深度越大。
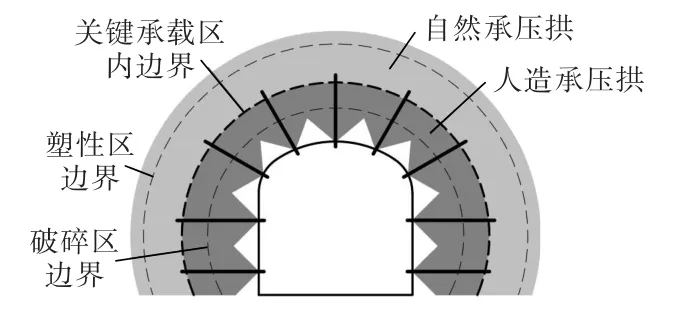
图14 深部巷道锚杆支护示意Fig.14 Schematic of rockbolt support in deep roadway
4.3 对深部巷道围岩稳定性控制的启示
了解和掌握巷道围岩的损伤分区和承载结构特征对巷道稳定性控制具有重要意义。研究结果显示,在深部高应力条件下,不同地层围岩的损伤区和承载区结构具有显著差异,而且关键承载区深度对围岩损伤变形具有明显控制作用。这就要求在制定深井矿山高应力巷道支护方案时,需要根据各类围岩的实际损伤破坏特征,有针对性地选择恰当的支护方法和确定合理的支护参数。
以目前矿山常用的锚杆支护为例,锚杆长度是锚杆支护最重要的技术参数,但如何确定锚杆长度是锚杆支护设计的难点。通常做法是将锚杆端头锚固到围岩深部稳定岩层,或取锚杆有效长度大于塑性区深度,但研究和实践表明这2 种方法确定的锚杆长度都偏安全,容易造成支护浪费。另一种工程实践性很强的方法是根据围岩松动圈深度来确定锚杆长度,但松动圈测试现场实施难度大,而且很多测量结果并没有明显的松动圈界线。根据承压拱(或压力拱)支护理论[30-31],锚杆支护的主要作用是在围岩损伤区内重建人造承压拱,提高损伤围岩的整体强度和自承能力,以此来抵抗围岩变形压力和维护巷道稳定。这也符合深部巷道围岩稳定性控制的基本原理[23]。结合承压拱支护理论和本文研究结果,综合分析认为较为合理的做法将锚杆锚固到围岩关键承载区内,即取锚杆有效长度等于围岩关键承载区的内边界深度(图14)。这样既避免了锚杆过长浪费,也避免了因锚杆支护长度不足所导致的围岩控制不稳。
5 结 论
针对深井矿山高应力巷道围岩稳定性控制问题,以云南某深井开采矿山1 500 m 埋深中段石门巷道为例,采用弹塑性理论分析、松动圈现场测试和数值模拟计算3 种方法,研究了深井高应力复杂地层巷道围岩的损伤分区和承载结构特征及其对巷道稳定性控制的意义。
(1)根据巷道开挖后围岩损伤分区特征和应力分布规律,建立了深部巷道围岩承载结构理论模型,将深部巷道围岩承载区划分为塑性承载区、弹性承载区和关键承载区3 个部分,提出了确定各承载区范围的方法。
(2)围岩松动圈现场实测结果显示,该矿山深部巷道围岩松动圈深度总体变化范围0.9~1.9 m,平均1.38 m。其中:灯影组松动圈深度范围1.5 ~1.9 m,平均1.7 m;宰格组松动圈深度范围1.1 ~1.3 m,平均1.15 m;大塘组松动圈深度范围0.9 ~1.5 m,平均1.17 m;摆佐组松动圈深度1.5 m。
(3)通过3 种不同方法的综合研究和对比分析,揭示了该矿山深部巷道围岩的损伤区发育特征。数值模拟结果显示不同地层围岩的破碎区深度范围为0.92~1.63 m,平均1.20 m;塑性区深度范围为1.48~2.50 m,平均1.87 m。虽然所处的地应力环境相同,但不同地层围岩的损伤区深度存在明显差异,由大到小排序为:灯影组>栖霞—茅口组>宰格组>大塘组>摆佐组。
(4)基于深部巷道围岩承载结构理论模型和数值模拟计算结果,划分了该矿山深部巷道围岩的承载结构。不同地层围岩的承载区厚度差别不大,但承载区深度存在显著差异。关键承载区厚度范围为1.09~1.34 m,平均1.28 m;关键承载区内边界深度范围为1.22~2.18 m,平均1.58 m;不同地层关键承载区深度由大到小排序为:灯影组>栖霞—茅口组>宰格组>大塘组>摆佐组。
(5)在巷道规格和地应力环境相同条件下,岩体强度是影响围岩承载结构和巷道稳定性的最主要因素。总体而言,岩体强度越大,关键承载区深度越小,围岩损伤区深度越浅,围岩变形量越小,巷道越稳定。
(6)巷道围岩损伤分区和承载结构研究结果为矿山深部高应力巷道稳定性控制与支护参数选取提供了理论依据。针对锚杆支护,提出锚杆有效长度等于巷道围岩关键承载区的内边界深度是比较合理的取值。
