Co3Sn2S2 单晶的磁性和电-热输运性能*

祝鑫强 王剑 朱璨 罗丰 陈树权 徐佳辉 徐峰 王嘉赋 张艳 孙志刚†

1) (武汉理工大学,材料复合新技术国家重点实验室,武汉 430070)

2) (武汉理工大学理学院,武汉 430070)

3) (太原科技大学材料科学与工程学院,太原 030024)

Co3Sn2S2 是一种磁性外尔半金属,具有特殊的磁性和电子结构,其独特的能带结构使其拥有反常霍尔效应、负磁阻效应和反常能斯特效应等多种物理性质.本文采用自熔剂法合成了高质量的Co3Sn2S2 单晶,并研究了Co3Sn2S2 低温下的电输运行为(磁阻效应与霍尔效应等)和热输运行为(塞贝克效应).热磁曲线表明,在居里温度点(TC=178 K)以下140 K(TA)处存在特殊的磁结构,为铁磁态与反铁磁态共存的磁性过渡态.研究发现,在100—160 K 出现负的反常“凸形”磁阻,且在TA 附近出现最大临界磁场B0,为1.41 T,同时霍尔电阻率ρyx 也在TA 处取得最大值约20 µΩ·cm.这可能是由于铁磁态与反铁磁态之间会相互竞争形成非平凡的自旋织构,导致TA 附近独特的电输运行为.Co3Sn2S2 在低温下的散射机制为声学波散射和电子-声子散射的共同作用,在60—140 K 时,自旋无序的增强会引起电子-声子散射增强,使得的塞贝克系数S 出现平台特征.研究表明,Co3Sn2S2 在低温下的特殊磁结构和电子自旋对其电-热输运行为有着重要影响.

1 引言

磁性Weyl 半金属Co3Sn2S2是一种具有kagome网状结构的拓扑材料,这种低维结构会导致其具有高结构态密度N(E),此外,其奇异的电子结构[1,2]也引起了人们的研究兴趣.其还具有一些其他的特殊性质,例如半金属性,其中,在费米能级(EF)处,自旋极化能带结构在自旋方向向上呈现半金属间隙,而另一个自旋方向则是金属性的,这是其自旋电子学应用的关键.其特殊的磁性和电子结构使它具有诸如反常霍尔效应[3−7]、反常能斯特效应[8−11]、巨磁光响应[12]等多种物理性质,目前已成为研究特殊磁性结构的重要平台.研究发现,Co3Sn2S2在低温下存在反常的磁性过渡态.其在居里温度以上为顺磁态,随着温度降低,磁序重排形成ab平面内的三角状反铁磁序;温度继续降低,磁序趋向于沿着c轴排列形成铁磁序,形成铁磁序与反铁磁序共存的反常的磁性过渡态;而当温度进一步降低时,完全转化为铁磁序[13−18].Guguchia 等[19]通过µ子自旋实验,发现了Co3Sn2S2存在竞争磁序的证据并对其进行定量分析,结果发现Co3Sn2S2在低温下表现为沿c轴的平面外铁磁态,但在90 K 以上会出现平面内反铁磁态,且随着温度升高反铁磁态的比例不断增大,在170 K 左右时达到80%,随着温度继续升高,在TC以上Co3Sn2S2表现为顺磁态,此外他们还发现Co3Sn2S2中的磁竞争以及磁有序分数与反常霍尔电导之间具有密切关系.

Weyl 半金属常伴随有巨磁阻效应,负磁电阻等磁输运行为[20].研究者使用Co3Sn2S2单晶、微带等不同样品[6,20−22]进行实验,在B⊥I,2 K,9T的条件下,获得了30%—150%范围的磁阻,磁阻范围较大的原因可能与晶体质量的不同有密切关系[23].一些研究者发现在100—150 K 存在异常的负磁阻,将其归因于自旋无序散射的作用[24].在Weyl 半金属中,当施加的外加电场与磁场平行时,倒空间中不同手性间的散射由于正负手性Weyl点间的距离增大而导致相应的谷间散射减弱,从而产生负磁阻效应[25].同时Co3Sn2S2具有显著的反常霍尔效应,其反常霍尔电导率和反常霍尔角分别达到1130 Ω–1·cm–1和20%,这比典型的磁系统要大1 个数量级.其巨大的反常霍尔电导与反常霍尔角来源于Co3Sn2S2的低载流子浓度和拓扑能带结构增强的贝里曲率[6].Co3Sn2S2的能带结构计算表明,费米能级附近区域主要由Co 3d 态组成,来自Sn 5p和S 3p 态的贡献较小,由此产生的EF处DOS 尖峰可能导致相对较高的塞贝克系数,而其表现为金属导电性,这引发了研究者对其热电性能的兴趣[26].

研究表明,Co3Sn2S2的许多物理性质如磁阻等都与晶体质量密切相关,获得质量较高的单晶对于物理性能的研究至关重要.本文通过自熔剂法制备得到了质量较高的Co3Sn2S2单晶(归一化电阻率ρ3 K/ρ300 K=0.08),并对其低温磁性以及低温下的磁阻性能、反常霍尔效应和塞贝克效应进行研究.发现Co3Sn2S2在140 K 附近存在特殊的磁结构,为铁磁态与反铁磁态共存的磁性过渡态,这种反常磁态使得在100—160 K 大范围出现“凸形”磁阻特征,且在TA附近出现最大临界磁场B0,为1.41 T,同时其霍尔电阻率ρyx也在TA处取得最大值约20 µΩ·cm.其竞争的磁性对其电输运性能产生了明显的影响.Co3Sn2S2在低温下的散射机制主要分为3 个区域,在60 K 以下为声学波散射和电子-声子散射共同作用;在60—140 K 时,随着自旋无序的增强,使得电子-声子散射增强,电子-声子散射占总散射的比重开始增大;当温度升至140 K 以上时,以声学波散射为主.这种散射机制的变化使得的塞贝克系数S在60—140 K 附近出现平台,功率因子PF 在60 K 取得最大值,值为18.1 µW/(cm·K2).

2 实验

2.1 材料制备

采取自熔剂法制备Co3Sn2S2单晶[22,27,28].首先,按照化学计量比称重高纯的Co 粒、Sn 粒、S粒放入圆柱形氧化铝坩埚中,再置于石英玻璃管中,随后抽真空进行密封.将密封好的石英管缓慢加热至400 ℃,保温2 h;接着在6 h 内升温至1000 ℃,保温10 h,然后在4 d 中,缓慢降温至800 ℃,随后缓慢冷却至室温.采用金刚石线切割机将材料切割成规则形状,用于磁性/电输运性能/热电性能的测量.

2.2 结构与性能表征

为研究所制备样品的相组成,采用德国布鲁克公司D8Advance 粉末衍射仪,在Cu Kα 辐射(λ=1.5418 Å)及室温条件下,获得了粉末测试样品(过200 目筛)的XRD 谱图.通过GSAS 软件对XRD数据进行精修[29].为观测样品的微观形貌,采用日本电子株式会社JSM 7500F 扫描电子显微镜(SEM)得到样品的二次电子图像(SE),并用该仪器配备的英国牛津仪器公司X-Max N80 型能量色散X 射线能谱仪(EDS)对样品进行成分分析.

采用Versalab 测量了H∥c轴,50—300 K 时场冷(FC)和零场冷(ZFC)下Co3Sn2S2单晶样品的磁热(M-T)曲线,并在8000 Oe 磁场下对H∥c轴,50—300 K 范围内的样品的磁化(M-H)曲线进行了测量,其中在50 K,100 K,150 K 下测量施加3 T 磁场,H∥c轴与H⊥c轴下样品的M-H曲线.对于ZFC 和FC 曲线的测量,分别在0 磁场下和50 Oe 磁场下从300 K 降至50 K,再在50 Oe磁场下进行升温测量.采用PPMS-9 测量了样品7 T 磁场下,3—300 K 的磁阻性能,施加的电流为400 µA.此外,还对3 K 下的样品进行了转角测量(磁场B与电流I的夹角范围为0°—90°).利用电输运性质测量系统(ET9000,东方晨景公司)测量了样品的霍尔效应与低温下的塞贝克效应,霍尔测量过程中分别施加了0.5 T 的正向和反向磁场.使用四探针法测量霍尔效应,但由于测量霍尔效应时能斯特效应,爱廷豪森效应等副效应也会对测量的结果造成影响,为了获得准确的霍尔数据,进一步应用对称化处理来获得准确的霍尔信号,ρyx=[ρyx(+B)–ρyx(–B)]/2.由于Co3Sn2S2在50 K以上都是以单一载流子为主[6],所以通过nH=1/(eRH)与µH=σRH计算得到霍尔载流子浓度nH与霍尔迁移率µH.

3 结果

图1(a) 为使用GSAS 软件进行Rietveld 精修拟合的X 射线衍射数据.使用R-3m空间群对数据进行精修,仅存在Co3Sn2S2对应的峰,这表明样品是单相的.通过Rietveld 精修得到的菱形结构六方设置下的晶格参数a,b,c,其中a=b=5.3691 Å和c=13.1765 Å,晶体的a,b和c值与文献[6]一致 (a=b=5.3689 Å和c=13.1762 Å).其中wRp=4.01%,Rp=2.38%,均小于10%,这说明样品的精修程度令人满意,证明形成了结晶性较好的纯相.图1(b) 为Co3Sn2S2的晶体表面XRD结果.在X 射线衍射数据中观察到3 个峰,可与六方晶体结构中的ab平面对应,Co3Sn2S2的其他晶面所对应的峰的缺失表明样品具有良好的单晶性质.插图显示的是所制备的片状单晶,尺寸约为8 mm×7 mm×0.5 mm.

图1 (a) Co3Sn2S2 的粉末XRD 结果,黑×表示测量的衍射峰强度,红线为计算的衍射峰强度,蓝色的线条表示计算计算数据与测量数据之差,绿色的线条表示Bragg 衍射峰的位置;(b) Co3Sn2S2 的晶体表面XRD 结果,XRD 的峰对应于六方晶格的ab 平面,插图为Co3Sn2S2 晶体的光学影像Fig.1.(a) Powder XRD results of Co3Sn2S2,black × represents the measured diffraction peak intensity,the red line represents the calculated diffraction peak intensity,the blue line represents the difference between the calculated data and the measured data,and the green line represents the position of the Bragg diffraction peak;(b) XRD results of the crystal surface of Co3Sn2S2.The peak of XRD corresponds to the ab plane of the hexagonal lattice.The insert shows the optical image of Co3Sn2S2 crystal.

图2(a)为Co3Sn2S2在2000 倍下SEM 图像.单晶自由面表现出明显的层状生长特征,这说明Co3Sn2S2晶体是沿着c轴方向生长的[30],与图1(b)中XRD 结果一致.图2(b)为EDS 面扫区域的样品形貌,图2(c)—(e)为EDS 的面扫描图像.其中Co,Sn,S 三种元素在材料中均匀分布,Co∶Sn∶S=2.751∶2.022∶2,与化学计量比大致相当.

图2 (a) Co3Sn2S2 样品在2000 倍下的表面SEM 结果;(b) EDS 面扫区域形貌;(c)—(e) Co3Sn2S2 样品的EDS 面扫描结果Fig.2.(a) Surface SEM results of Co3Sn2S2 sample at 2000 times;(b) EDS surface scanning area morphology;(c)–(e) EDS surface scan results of Co3Sn2S2 sample.

图3(a)为零场下Co3Sn2S2单晶样品的电阻率随温度变化的曲线.电阻率随温度的升高而升高,表现出明显的金属行为,在178 K 处出现一个尖锐的扭折,这与其铁磁相变对应,178 K 为其居里温度.图3(b)为以300 K 下的电阻率为基准的归一化电阻率ρ/ρ300 K随温度的变化曲线,虚线为报道文献中的数据[6,7,15,31].同一材料的归一化电阻率会由于杂质的数量和其他晶体缺陷而表现出较大的差异.材料的杂质与晶体缺陷越少,其归一化电阻率越小,归一化电阻率可以作为判断晶体质量的一个标准.将归一化电阻率ρ/ρ300 K与文献中的样品进行对比[6,7,15,31],在约120 K 以上,归一化电阻率的值都基本一致,当降至120 K 以下时,归一化电阻率曲线开始呈现出不同的下降速率,在3 K下样品的归一化电阻率的值较小,ρ3 K/ρ300 K=0.08,较其他研究测量的归一化电阻率值0.19 小1/2 以上,说明样品的晶体质量处于较高水平.

图3 (a) 零场下Co3Sn2S2 的电阻率ρ 随温度变化的曲线,插图为电阻率测量原理图;(b) 以 300 K 下的电阻率为基准的归一化电阻率 ρ/ρ300 K 随温度的变化曲线,虚线是文献[6,7,15,31]中报道的样品的归一化电阻率Fig.3.(a) Temperature dependence of resistivity ρ of Co3Sn2S2 at zero field,the insert is diagram of resistivity measurement;(b) temperature dependence of normalized resistivity ρ/ρ300 K based on resistivity at 300 K.The dotted line is the normalized resistivity of the sample reported in Ref.[6,7,15,31].

首先对其磁性能进行研究.图4(a)为50 Oe磁场下,H∥c时Co3Sn2S2的ZFC 和FC 曲线.磁化强度在居里温度处突然降低,这与报道的铁磁相变相对应[32].插图为磁化强度的一阶微分随温度的变化关系,可以明显看出在178 K 处取得最小值,对应于居里温度TC.在居里温度以下时,ZFC与FC 曲线出现一个比较大的分岔.对于FC 曲线,磁化强度随着温度的升高不断降低;对于ZFC 曲线,50—130 K 时磁化强度随温度升高而增大,在130 K 出现极大值,随着温度继续升高,磁化强度开始下降,在140 K 附近ZFC 曲线出现极小值点TA,在140 K 以后磁化强度随温度升高继续增大,到TC附近时,与FC 曲线重合.TA附近磁化强度的反常降低表明Co3Sn2S2在居里温度以下可能存在着特殊的磁结构[13−15,33,34].Guguchia 等[19]通过µ子自旋实验,指出Co3Sn2S2的kagome 晶格中存在竞争磁序的证据.他们的实验结果表明在Co3Sn2S2在90 K 以下为铁磁态,磁矩沿着c轴有序排列;随着温度升高,部分磁矩重排形成ab平面内的三角状反铁磁序,形成铁磁序与反铁磁序共存的反常磁性过渡态;温度继续升高至居里温度TC以上,磁矩在热驱动下趋于无序排列,表现出顺磁态.他们还发现铁磁序的体积分数与反常霍尔电导呈负相关的关系.Zhang 等[15]进一步利用非弹性中子散射和密度泛函理论(DFT)计算并证明了Co3Sn2S2中铁磁序与反铁磁序两相共存的理论模型的可行性.Liu 等[33]通过弹性中子散射发现Co3Sn2S2在居里温度以下面内磁序的存在,这也对Co3Sn2S2单晶在TA附近存在铁磁序与反铁磁序共存的磁性过渡态提供支持.此外,一些研究[16,18]通过磁光谱学、磁显微镜以及磁性测量等手段提供了Co3Sn2S2中磁性过渡态可能存在的证据.图4(b)为Co3Sn2S2的H∥c与H⊥c时的M-H曲线.当H∥c时,M-H曲线在2000 Oe 磁场以内就可以很快达到饱和,且随着温度降低,饱和磁化强度不断增大;而当H⊥c时,M-H曲线在30000 Oe 磁场下仍然没有饱和的趋势,在50 K,100 K,150 K 的曲线比较接近.在相同温度下,H∥c与H⊥c时,M-H曲线表现出较大的差异,这说明样品具有强磁晶各向异性.图4(c)为2000 Oe 磁场以内H∥c时不同温度下Co3Sn2S2的M-H曲线.在50—120 K下,M-H曲线表现出明显的矩形特征,且随着温度的升高,矩形的面积不断减小.当温度升到140—175 K 之间时,磁化曲线不再是矩形.磁化强度随磁场增大而线性增大,在饱和磁场处磁化强度达到饱和,然后随磁场增大缓慢上升.此时的磁滞很小.在200 K 时,磁化曲线转化为线性,表明此时的样品为顺磁态.由图4(c)可以得到H∥c时Co3Sn2S2的饱和磁化强度MS与矫顽力HC随温度变化的曲线,见图4(d).图中也标出了TA和TC.在TA以下,样品处于铁磁态,随着温度升高,MS与HC线性降低;当温度升至TA附近时,其MS不为零,而HC几乎降为零;当温度继续升至TC时,MS急剧降低,这是由铁磁相变引起的.在50 K 时,饱和磁化强度MS为11.54 A·m2/kg,矫顽力HC为840 Oe.

图4 (a) H∥c 轴,磁场为50 Oe 时,Co3Sn2S2 样品的磁化强度M 随温度的变化曲线,插图展示的是磁化强度的一阶微分dM/dT随温度变化曲线;(b) H∥c 轴,H⊥c 轴,在50 K,100 K,150 K 下磁化强度M 随磁场H 的变化曲线: (c) H∥c 轴,在50—300 K 下的磁化强度M 随磁场H 的变化曲线;(d) H∥c 轴,饱和磁化强度MS 和矫顽力HC 随温度的变化曲线Fig.4.(a) H∥c axis,the magnetic field is 50 Oe,the temperature dependence of the magnetization M of Co3Sn2S2.The insert shows the dM/dT with T;(b) H∥c axis,H⊥c axis,magnetic field dependence of magnetization at 50 K,100 K,150 K;(c) H∥c axis,M-H at 50–300 K;(d) H∥c axis,the temperature dependence of the saturation magnetization MS and coercivity HC..

图5(a)给出B∥I时,7 T 磁场下单晶Co3Sn2S2磁阻随磁场的变化曲线.磁阻由公式RM=[ρxx(B)–ρxx(0)]/ρxx(0)来计算得到,ρxx(B)表示在磁场B下的电阻率,ρxx(0)表示零磁场下的电阻率.在温度低于60 K 时,磁阻为正磁阻,其与磁场表现为抛物线形关系.当温度达到60 K 附近时,出现正负磁阻的转变,在60 K 处表现为抛物线形的负磁阻.在100—160 K 时,磁阻呈现出“凸形”特征,磁阻曲线由两段不同曲率的负抛物线组成.当磁场较小时,抛物线曲率较大,负磁阻随磁场的增大迅速增大;到达某个临界磁场以后,抛物线曲率大幅降低,负磁阻随磁场的增大而缓慢增大.我们称磁阻曲率变化的转变磁场为临界磁场B0.当温度进一步上升至TC以上时,磁阻重新转化为抛物线形的负磁阻.图5(b)为B∥I时,B=7 T 下磁阻随温度变化的曲线.在约60 K 以下,呈现明显的正磁阻,在60 K 处出现正负磁阻的转变,此后一直表现为负磁阻,在居里温度以上,磁阻几乎消失.这种正负磁阻的转变主要归因于洛伦兹力对磁阻的正贡献和自旋无序的负贡献的相互竞争.Shivam 等[23]在研究晶体质量对Co3Sn2S2的电输运行为影响时,发现两个不同晶体质量的样品的正负磁阻的转变温度分别约为22 K (ρ2 K/ρ300 K=0.18)与67 K (ρ2 K/ρ300 K=0.06).其中晶体质量较高样品的正负磁阻的转变温度与本文测量得到的转变温度值相近.图5(b)插图为临界磁场B0随温度的变化关系.可以看出临界磁场B0随温度升高先增大后减小,在TA(140 K)处取得最大值1.41 T,与此对应其负磁阻大小也有相似的变化,在TA处取得最大的负磁阻约–3.1%,这与TA处特殊的磁结构所对应,其平面内三角状反铁磁矩与铁磁矩的相互竞争可能是造成这种特殊磁阻现象的原因.为了更好理解磁阻RM随磁场的变化规律,图5(c)中给出了3 K 时的磁阻曲线以及使用MR=aB2+cB对该曲线拟合的结果.拟合结果得到a=0.4246,c=1.7112,这说明磁阻随磁场的变化由线性贡献和抛物线贡献共同组成[35].为了进一步理解磁阻与磁场的关系,对图5(d) 中3 K 时不同角度下的RM-B曲线都进行拟合,结果如表1 所示.随着B与I夹角从0°增至90°,a,c都不断增大,但它们的比值都在0.25 左右,这说明B与I的夹角的变化不会对其磁阻来源的贡献造成影响.进一步研究了磁阻随温度变化的一阶导数与温度的关系,见图5(c)的插图.发现dMR/dB随磁场B的增大线性增大,没有观察到饱和的现象,这说明在7 T 磁场以内,磁阻的贡献由洛伦兹力对电子的偏转占主导地位.Nagpal 和Patnaik [20]对B⊥I,2 K 下,0—12 T 的Co3Sn2S2单晶的磁阻效应进行研究,发现在8 T 以上出现线性磁阻.在Abrikosov[36]提出的理论中,在费米能级附近表现出线性体带交叉的系统中,线性磁阻发生在量子区,其中所有电子都被限制在最低朗道能级,带电粒子表现为相对论性狄拉克费米子.Nagpal 和Patnaik[20]认为当受到外加磁场作用时,由于电荷载流子轨道运动的量子化,形成了具有线性能量色散关系的量子化朗道能级,所有载流子填充在最低朗道能级上,表现为狄拉克费米子,导致Co3Sn2S2产生线性磁阻.目前的研究认为,在Weyl 半金属中,当施加的外加电场与磁场平行时,由于手性反常而产生负磁阻效应[25].为了验证Co3Sn2S2中的手性反常,测量了3 K 下B与I在不同夹角下的磁阻MR,如图5(d)所示.研究发现,在不同角度下的磁阻曲线都表现为抛物线形的正磁阻.Nagpal 和Patnaik [20]以及Shama等[24,37]通过研究也发现在不同角度下磁阻曲线均表现为抛物线形的正磁阻.他们认为可能是Co3Sn2S2中较大的正磁阻会掩盖负磁阻的存在,此外样品内部不均匀电流分布引起的电流喷射效应[38]也会使得难以观察到负磁阻现象.在3 K,7 T 磁场作用下的MR 随角度的变化如图5(d)插图所示,当B⊥I时,磁阻取得最大值约35%,随着B转向I,磁阻不断减小,在B∥I时,取得最小值约8%.这是因为Co3Sn2S2是一种具有强磁晶各向异性的材料,其易磁化轴是c轴.使用正弦函数对磁阻随B与I夹角变化的曲线进行拟合,拟合程度很高.磁阻随B与I夹角θ的变化具有反转对称性与C2x对称性.反转对称性指Co3Sn2S2的磁阻在当B⊥I时取得最大值,随着B转向I,磁阻则不断减小,磁阻大小关于θ=+kπ(k为整数)对称.C2x对称性指MR(θ)=MR(π+θ).Shen 等[14]通过对Co3Sn2S2的磁晶各向异性性能进行研究,得到了在2 K,500 Oe 磁场下的磁化强度随B与c轴角度的变化关系,同样呈现出反转对称性与C2x对称性.

表1 使用公式MR=aB 2+cB 拟合B 与I 在不同夹角下的MR-B 曲线得到的拟合值Table 1.The fitting values of the MR-B curve according to the formula MR=aB2+cB at different angles between B and I.

图5 (a)当B∥I 时,3—220 K 的磁阻曲线;(b) 当B∥I 时,B=7 T 下磁阻MR 随温度变化曲线,插图为100—160 K 的“凸形”磁阻的临界磁场B0 随温度变化曲线;(c) 当B⊥I 时,3 K 下磁阻MR 随磁场的变化,黑色的实线表示根据公式拟合的值(MR=aB2+cB),插图为3 K 下dMR/dB 随磁场的变化;(d) 3 K 下,磁场B 与电流I 在不同夹角下的磁阻变化曲线,插图为MR 随夹角变化的曲线,红色实线为使用正弦函数拟合的值Fig.5.(a) B∥I,the magnetoresistance(MR) curve of 3–220 K;(b) B∥I,the curve of MR versus temperature at B=7 T,the insert is the critical point B0 of “convex” MR versus temperature at 100–160 K;(c) B⊥I,the MR versus the magnetic field at 3 K,the black solid line represents the value fitted according to the formula (MR=aB 2+cB),and the insert shows the dMR/dB versus the magnetic field at 3 K;(d) the MR of different angle between the B and I versus the magnetic field B at 3 K,and the insert is the MR versus different angles,the red solid line represents the value fitted according to sine function.

为了对电输运行为有更深入的理解,测量了20—300 K 下Co3Sn2S2的霍尔电阻率ρyx随磁场的变化曲线,如图6(a)所示.与磁化强度的曲线相似,在居里温度以下表现出明显的磁滞现象.ρyx随着磁场增大迅速趋于饱和,并随着磁场继续增大,继续缓慢增大.此时霍尔系数为正值,空穴载流子在输运过程中占主导地位,Liu 等[6]通过对霍尔效应的研究也得到Co3Sn2S2在高于50 K 时空穴载流子主导输运过程.当温度升至居里温度以上时,磁滞消失,ρyx表现为一条平滑的曲线.矫顽力HC随温度升高而降低,为明显的铁磁材料特征.图6(b)为Co3Sn2S2的反常霍尔电导和霍尔电阻率ρyx随温度变化的曲线.反常霍尔电导通过来计算.发现霍尔电阻率ρyx随温度的升高先增大后减小,在TA=140 K附近取得最大值约20 µΩ·cm,Wang 等[7]在对Co3Sn2S2的反常霍尔效应进行研究时在5 K下获得了约21 µΩ·cm 的饱和霍尔电阻率,与本文测量值相近.在100 K 以下随温度变化不大,约1.4×103Ω-1·cm-1,这是由于其是由内禀的Berry 曲率产生的,受到拓扑保护,具有鲁棒性[6],在较低温度下的热激发不足以对其造成影响,而随着温度升高,热激发加剧,使得拓扑保护被破坏,急剧降低.计算的反常霍尔角如图6(c)所示.Co3Sn2S2的反常霍尔角随着温度的升高先增大后减小,在140 K 取得最大值约为16%.Liu 等[6]通过研究发现,Co3Sn2S2中存在较大的反常霍尔电导与反常霍尔角,其数值分别达到1130 Ω–1·cm–1和20%,这与我们测量的值相近.图6(d)和图6(e)为通过霍尔电阻率ρyx获得的Co3Sn2S2载流子浓度n和载流子迁移率µ随着温度的变化曲线.发现随着温度升高,载流子浓度n单调上升,这是因为随着温度升高,热运动加剧,电子与空穴受激发而挣脱共价键而使得载流子浓度增大,Nagpal 和Patnaik [20]研究发现在50 K 以下时,Co3Sn2S2的载流子浓度随温度的升高不断增大,与我们的研究结果一致.而在居里温度之后的载流子浓度斜率较低温时减小,这可能是因为铁磁相变的影响.如图6(e)所示,载流子迁移率µ则随着温度的升高而单调降低,在20 K 时,载流子迁移率µ取得最大值,约2.7×103cm2/(V·s).可以根据lnµ-lnT曲线的斜率对材料的散射机制进行分析,可以看到曲线在60 K 和140 K 处的斜率发生了改变,分别对其进行线性拟合,如图6(e)插图所示.对于处于绝对零度以上的晶体,其不可避免地存在着晶格本身的热振动,载流子在晶体中的运动偏离晶格的周期性,导致散射的发生.晶体振动对载流子的散射可以归结于各个格波对载流子的散射,包括声学波和光学波.对于单晶化合物材料,其散射机制主要以声学波散射为主.其中简并态材料的声学波散射的迁移率µ与温度的关系为µ-T–1[39].Fivaz 等[40]对层状材料进行研究,发现电子与声子之间会发生相互作用.根据电子和晶格之间耦合的强度,这种涉及短程力的相互作用会导致载流子被束缚或被释放,从而使得迁移率µ与温度的关系为µ-T–β,其中GaSe 的β值可以达到2.2,而MoS2的β值可以达到2.4,较声学波散射的值大很多.我们得到了lnµ-lnT曲线在60 K 以下的斜率约为–1.7,处于声学波散射与电子-声子散射的值之间,这说明此时Co3Sn2S2的散射机制为声学波散射和电子-声子散射共同作用;在60—140 K 时斜率降低至–2.2,此时Co3Sn2S2的自旋无序增强,使得电子-声子散射增强;当温度升至140 K 以上时,斜率升高至–1.3,与–1 接近,–1 对应于简并态材料声学波散射的散射因子大小,这说明此时Co3Sn2S2的散射机制以声学波散射为主.

图6 (a) 不同温度下Co3Sn2S2 的霍尔电阻率ρyx 随磁场变化的曲线,插图为霍尔电阻率测量原理图;(b) 反常霍尔电导率 与霍尔电阻率ρyx 随温度变化的曲线;(c) 反常霍尔角/σ 与随温度变化的曲线;(d) 载流子浓度n 随温度变化曲线;(e) 载流子迁移率µ随温度变化曲线,插图为ln µ随ln T 的变化曲线Fig.6.(a) Hall resistivity ρyx versus the magnetic field of Co3Sn2S2 at different temperatures,the insert is the diagram of Hall resistivity measurement;(b) the temperature dependence of abnormal Hall conductivity and Hall resistivity ρyx;(c) the temperature dependence of abnormal Hall angle /σ;(d) the carrier concentration n versus the temperature;(e) the carrier mobility µversus the temperature,the insert is the ln µ versus ln T.

接下来对Co3Sn2S2的热电输运行为进行研究,图7(a)—(c)分别是单晶Co3Sn2S2的电导率σ,塞贝克S,功率因子PF 随温度变化的曲线.我们发现σ随温度升高单调降低,且随着温度升高其下降速率不断减慢.在图6(c)—(d)中得到,载流子浓度n随着温度升高单调增大,而载流子迁移率µ随着温度的升高不断降低.根据σ=neµ,电导率σ的变化规律与载流子迁移率一致,这说明载流子迁移率对电导率σ的贡献占主导地位.其塞贝克系数S在整个温度区间都是负值,说明Co3Sn2S2中电子在输运过程中占主导地位,这与霍尔测量得到的结论不一致,这是可能是由于其是由多种载流子共同调控输运的[41].在300 K 时,塞贝克的值约为–45 µV/K,这与文献[8,42,43]中的值–35—–60 µV/K 接近.S随着温度的降低而减小,在居里温度处出现扭折点,对应于铁磁相变[42].在60—140 K 处S基本保持不变,在低于60 K 时S继续减小,在20 K 处取得最小值,为–11 µV/K.图7(c)给出了功率因子PF=S2σ随温度的变化关系.当温度低于60 K 时,PF 随温度升高而急剧上升,并在60 K 取得最大值约18.1 µW/(cm·K2).在60—140 K 时,PF 随温度的升高而降低,随着温度的继续上升,PF 呈缓慢上升趋势.由PF=S2σ,可得到PF 的变化由塞贝克系数S与电导率σ的变化共同调控.在60 K 以下,塞贝克系数S大幅提升,而电导率σ降低,塞贝克系数的变化占主导,PF大幅提升;在60—140 K,塞贝克系数S基本保持不变,而电导率σ降低,PF 急剧降低;在140 K 以上,塞贝克系数S缓慢提升,电导率σ缓慢降低,塞贝克系数的变化占主导,PF 缓慢提升.

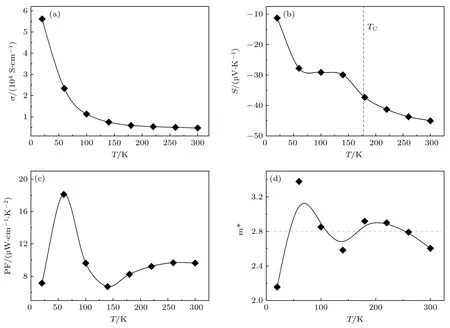
图7 (a) Co3Sn2S2 的电导率σ 随温度变化的曲线;(b) 塞贝克系数S 随温度变化的曲线;(c) 功率因子PF 随温度变化的曲线;(d) 使用载流子输运的能带模型计算获得的有效质量m* 随温度变化的曲线Fig.7.Temperature-dependent (a) conductivity σ,(b) Seebeck coefficient S,(c) power factor PF of Co3Sn2S2;(d) effective mass m*calculated according to the energy band model of carrier transport.

通过载流子输运的能带模型[44],使用 (1)—(3)式计算了Co3Sn2S2的有效质量m*,如图7(d)所示.

其中kB为玻尔兹曼常数,约为1.38×10-23J/K;e为电荷量,约为1.6×10-19C;h为普朗克常数,约为6.63×10-34J·s;λ为散射因子;η=EF/(kBT)为简约费米能级,x=E/(kBT)是简约载流子能量,n可取整数或者半整数.

通过计算得到20—300 K 的有效质量m*.Co3Sn2S2的m*在300 K 以下随温度的变化不大,在约2.8m0附近波动.这说明m*对热电输运的影响不大,热电输运过程主要受载流子浓度与散射机制的影响.Liu 等[6]通过对Co3Sn2S2的Shubnikovde Haas(SdH)量子振荡进行研究,得到Co3Sn2S2的有效质量为3.9m0,与本文测量值相近.

通过 (1)—(3)式,可以得到材料的塞贝克系数S与载流子浓度n的关系式:

对于Co3Sn2S2单晶,其有效质量在300 K 以下随温度的变化不大,材料的塞贝克系数主要受温度T、载流子浓度n以及散射因子λ的影响.Co3Sn2S2的载流子浓度n随温度的升高不断增大.当散射因子不变时,塞贝克系数S受温度和载流子浓度的共同作用,其中塞贝克系数变化与温度变化呈正相关,与载流子浓度变化呈负相关.在60 K 以下时,温度的贡献占主导地位,塞贝克系数随温度升高而增大;在60—140 K 时,受自旋无序的影响,电子-声子散射增强,温度对塞贝克系数的提升受到抑制,温度与载流子浓度的贡献基本相近,产生平台状特征;随着温度的继续升高,温度对塞贝克系数的贡献重新占据主导地位,塞贝克系数随温度升高而增大.

为进一步阐明Co3Sn2S2的磁性和电-热输运性能的联系,我们将在本文中获得Co3Sn2S2的磁性能曲线(磁热曲线、MS曲线和HC曲线)、电输运性能曲线(曲线、ρyx曲线和MR 曲线)和热电输运性能曲线(S曲线)进行归一化处理,并重新绘制在一起,见图8(a)和图8(b).图8(a)中通过对磁热曲线进行分析得到Co3Sn2S2的居里温度TC为178 K,并在TA=140 K 附近发现了特殊的磁结构,为沿着c轴的铁磁态与ab面的反铁磁共存的磁性过渡态,其中在TA处其铁磁态与反铁磁态可能形成一种特殊的临界状态,使得在MT曲线中呈现极小值点.受其磁结构影响,当温度升至TA附近时,Co3Sn2S2的矫顽力HC几乎降为零,霍尔电阻率ρyx取得最大值约20 µΩ·cm;当温度继续升至TC时,Co3Sn2S2发生铁磁相变,其饱和磁化强度MS,反常霍尔电导以及霍尔电阻率ρyx急剧降低,当温度继续上升时,其饱和磁化强度MS,反常霍尔电导以及霍尔电阻率ρyx继续降低,直至趋近于0.如图8(b)插图所示,通过霍尔电阻率ρyx的测量,得到载流子迁移率µ随温度的变化曲线,通过分析得到Co3Sn2S2在低温下的散射机制主要分为3 个区域,在60 K 以下为声学波散射和电子-声子散射共同作用;在60—140 K时,随着自旋无序的增强,使得电子-声子散射增强,电子-声子散射占总散射的比重开始增大;当温度升至140 K 以上时,以声学波散射为主.在图8(b)中,对Co3Sn2S2的磁阻曲线和塞贝克曲线进行协同分析.由于自旋无序的作用,在约60 K 附近时发现了正负磁阻的转变,同时塞贝克系数S开始出现平台状特征.在温度升至140 K 以上时,自旋无序的作用减弱,此时散射机制以声学波散射为主,塞贝克曲线的平台特征消失,塞贝克系数随温度升高而增大.其中在居里温度TC附近塞贝克曲线出现扭折,这是由于铁磁相变的影响.此外,在100 K以下时,样品呈现铁磁态,其磁阻与磁场表现为抛物线形关系;而在100—160 K 之间时,样品呈现铁磁态与反铁磁态共存的磁性过渡态,呈现“凸型”磁阻特征,其中在TA处特殊的磁性临界状态会使得“凸型”磁阻的临界磁场B0取得最大值;而当温度升至居里温度以上时,样品呈顺磁态,其磁阻与磁场表现为抛物线形关系.分析认为,当样品为单一磁态时,磁阻仅受洛伦兹力作用,磁阻随磁场变化呈抛物线型特征.而当样品为铁磁态与反铁磁态共存时,磁阻可能会受到自旋无序散射的影响,磁阻在自旋无序散射和洛伦兹力的竞争下而呈现出“凸型”磁阻特征.研究发现,Co3Sn2S2的磁结构和电子结构能通过控制材料的散射机制对其电-热输运性能进行调控.

图8 (a) Co3Sn2S2 的归一化饱和磁化强度MS,归一化矫顽力HC,归一化反常霍尔电导,归一化霍尔电阻率ρyx 随温度的变化曲线及归一化ZFC 与FC 曲线;(b) 归一化塞贝克系数S,归一化磁阻MR 随温度的变化曲线,插图为lnµ随lnT 的变化曲线Fig.8.(a) Temperature-dependent normalized saturation magnetization MS,normalized coercivity HC,normalized anomalous Hall conductivity ,normalized Hall resistivity ρyx and normalized ZFC and FC curves of Co3Sn2S2;(b) temperature-dependent normalized Seebeck coefficient S and normalized magnetoresistance MR,the insert is the lnµ versus lnT.

4 结论

本文通过自熔剂法制备了高质量的尺寸为8 mm×7 mm×0.5 mm 的Co3Sn2S2单晶.研究发现Co3Sn2S2的居里温度为178 K,在TA=140 K附近发现了特殊的磁结构,为沿着c轴的铁磁态与ab面的反铁磁共存的磁性过渡态,这种特殊磁结构导致在TA附近产生独特的电输运行为: 在100—160 K 的大范围出现负的反常“凸形”磁阻,且在TA附近出现的临界磁场B0最大,为1.41 T;同时霍尔电阻率ρyx也在TA处取得最大值约20 µΩ·cm.在约60 K 时发现了正负磁阻的转变,这种正负磁阻的转变主要归因于洛伦兹力对磁阻的正贡献和自旋无序的负贡献的相互竞争.其自旋无序的增强会引起电子-声子散射增强,使得温度对塞贝克系数的提升受到抑制,塞贝克系数S在60—140 K 附近出现平台特征.目前对于低温下磁结构和电子自旋的特征尚未完全解析清楚,其对于输运性能的影响还有待更深入的研究.