融合GA-CART和Deep-IRT的知识追踪模型
2023-09-18何廷年李爱斌毛君宇
郭 艺,何廷年,李爱斌,毛君宇
(西北师范大学计算机科学与工程学院,甘肃 兰州 730070)
1 引言
在线教育系统通过练习和考试来收集学生学习过程中的交互信息,并利用收集的数据提供个性化教育。在这其中,教育数据挖掘是在线教育系统中不可或缺的一部分,而知识追踪又是此领域中重要的研究方向。
知识追踪的目标是通过分析学生的知识储备以及知识状态来预测学生对知识的掌握水平。知识追踪问题可以描述为[1]:在练习集合Q={q1,q2,…,qn}中,通过学生与练习集合的交互操作,得到学生的观测序列{x1,x2,x3,…,xn-1},通过对观测序列的分析预测下次表现xn,通常xn={qn,rn},其中,qn表示回答的问题成分,也就是练习标签;rn表示对应的回答是否正确,通常rn∈{0,1},0表示回答错误,1表示回答正确。
近年来,深度学习强大的表征能力,促使大量基于深度学习的知识追踪模型涌现,极具代表性的有深度知识追踪模型DKT(Deep Knowledge Tracing)[2]、动态键值记忆网络DKVMN(Dynamic Key-Value Memory Network)[3]和深度项目反应理论Deep-IRT(Deep Item Response Theory)[4]等。DKT以循环神经网络RNN(Recurrent Neural Network)为基础结构[5],利用RNN中的隐藏状态表示学生的知识状态。DKVMN实现了对记忆增强网络MANN(Memory-Augmented Neural Network)的优化,提出了使用键值对矩阵作为内存结构,键(key)矩阵是一个静态矩阵,用来存储题目的知识成分,值(value)矩阵是一个动态矩阵,用来存储学生动态练习的知识状态。
根据教育心理学中的成败归因论,学习者答题过程中会因为努力程度、身心状态和心情等主观因素而对答题结果产生一定的影响。传统DKVMN模型未考虑到学生答题过程中的心理或行为特征对练习以及预测结果的影响,如答题过程中尝试答题的次数越多,学生可能产生的消极情绪越复杂,因此对答题的正确率影响越大,甚至影响之后所有的学习行为。相反,答题过程中尝试答题的次数越少,学生可能产生的积极情绪越多,因而答题的正确率越高。Sun等人[6]提出的加入决策树的方法对行为特征进行预处理,有效提升了模型的预测概率,但分类与回归树CART(Classification And Regression Tree)所使用的分类规则容易导致算法的预测结果陷入局部最优的“陷阱”,遗传算法GA(Genetic Algorithm)作为全局最优搜索算法之一[7],基于遗传算法的CART优化算法(GA-CART)[8,9]可以有效改进传统CART出现的局部最优问题,所以本文提出一种在Deep-IRT模型的基础上加强对学习者行为特征预处理的方法,以提高模型的预测性能。
本文的主要工作有:
(1)使用基于遗传算法的CART优化来对行为特征进行处理。这种方法可有效地对学生的行为特征进行个性化建模。
(2)将预处理优化后的模型与Deep-IRT模型相结合,提出了一种融合GA-CART和Deep-IRT的知识追踪模型DKVMN-GACART-IRT。
(3)将DKVMN-GACART-IRT模型在3个公开数据集上与DKT、DKVMN、Deep-IRT以及DKVMN-DT模型进行对比实验,实验结果表明DKVMN-GACART-IRT模型预测性能具有优势。
2 相关工作
2.1 DKVMN
在深度知识追踪模型的发展历史中,极具代表性的是DKT模型,但是其出现的可解释性差、长期依赖问题和学习特征少的问题[10-18],使得大量基于DKT模型的改进方案不断涌现。其中就有Zhang等人[3]提出的动态键值记忆网络DKVMN,该模型使用一对键值矩阵作为内存结构。静态键矩阵存储的是潜在知识概念,而动态值矩阵存储的是学生对概念的掌握程度。DKVMN采用离散的练习标记qt,输出响应概率p(rt|qt),然后使用练习和响应元组(qt,rt)更新内存,其中x1(q1,r1)表示一次交互信息,一次交互信息中包含有学生的练习标签q1以及答题情况r1。在每道题中包含有与之相对应的概念信息,即知识成分。一道题中可能有许多的知识成分,而这些知识成分在题目中的权重各不相同,这就需要用到注意机制来对每道题中的知识成分进行处理。这种采用键值对矩阵以及简单的注意机制的知识追踪模型,缓解了DKT因隐藏层单一向量空间导致的无法准确确定学生擅长或不熟悉的知识成分KC(Knowledge Component)的缺点。
2.2 Deep-IRT
Yeung等人[4]受贝叶斯深度学习的启发,综合了学习模型和心理测试模型对DKVMN模型进行改进,提出了Deep-IRT模型。Deep-IRT模型利用DKVMN模型处理输入数据,并返回IRT模型中有心理意义的参数。DKVMN模型执行特征工程任务,从学生的历史交互问答中提取潜在特征。然后,提取的潜在特征用于推断随时间变化的每个KC的难度水平和学生能力。基于对学生能力的估计和KC难度水平,IRT模型预测学生正确回答KC的概率[19]。Deep-IRT模型保留了DKVMN模型的性能,同时利用IRT模型为学生和题目难度提供了直接的解释。Deep-IRT模型使基于深度学习的知识跟踪模型具有可解释性。
2.3 DKVMN-DT
CART决策树具有不需要进行对数运算、计算开销相对较小、适合大数据等特点,Sun等人[6]受其启发,选用CART算法作为学生做题行为特征的预分类方法,提升了DKVMN模型行为特征预处理能力。
3 DKVMN-GACART-IRT
DKVMN-GACART-IRT模型结构如图1所示,该模型将GA-CART与Deep-IRT相融合,即结合行为特征预处理和心理测量学模型,预测学生正确答题的概率。
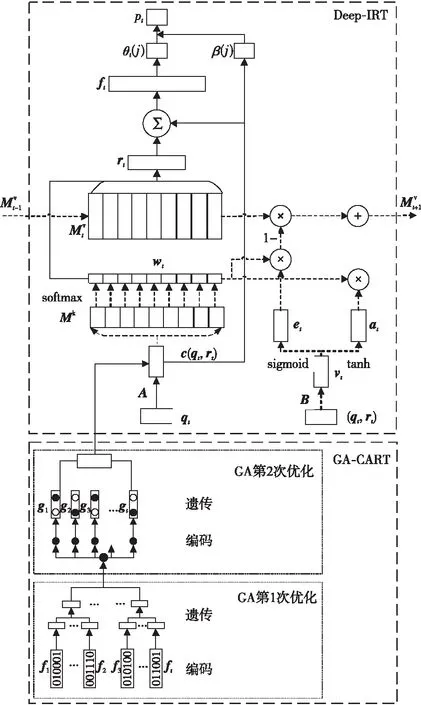
Figure 1 Structure of DKVMN-GACART-IRT model
3.1 行为特征预处理
数据预处理阶段主要对尝试次数、第1次响应和第1个动作等学生的行为特征进行基于遗传算法的CART分析。本文基于遗传算法的CART优化主要分为2步:第1步是对CART算法的上层进行GA优化,即将遗传算法应用到特征分类中,从而找到最优的特征来提高分类精度;第2步是对CART进行GA双层优化,即使用遗传算法替代二分法,从而找到决策树中的最优分叉点。
3.1.1 CART算法的上层GA优化
基于GA的CART上层优化主要是将遗传算法应用到特征分类中,从而找到最优的特征来提高分类精度。
(1)编码。本文采用二进制对所有个体进行基因编码,基因串位数等同于特征数,即将特征表示为由0与1组成的二进制基因序列,相当于一个二进制一维数组,其中1表示个体中的某一特征被选中,相反,0表示个体中的某一特征未被选中。多个这样的基因串组成初始种群,如图2所示,a、b、c、d为一个种群,a表示一个染色体,即一串基因序列,1或0表示基因编码。
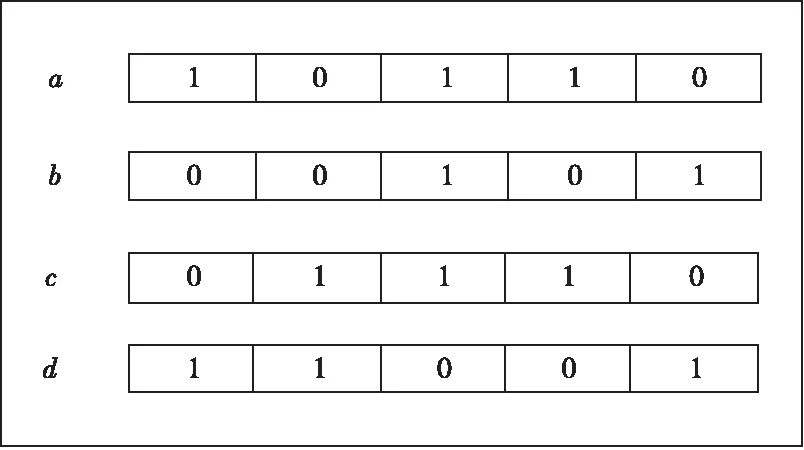
Figure 2 Population
(2)适应度函数。遗传算法通过适应度函数评判筛选个体,具有强适应性的个体中包含的高质量基因具有较高概率遗传给后代,而具有适应性弱的个体的遗传概率较低。本文中目标函数是以分类精度最大值为目标,故可直接利用目标函数值为个体的适应度值,准确率高的个体为最优个体。基于CART算法上层GA优化的适应度函数如式(1)所示:
fitness_s(xi)=acc_s(xi)
(1)
其中,xi表示种群中第i个个体,acc_s(xi)表示第i个个体xi在特征属性中的分类精度。
(3)遗传操作。遗传算法的操作包括选择、交叉和变异操作,选择操作先计算每个个体的个体适应度值,然后计算每一代遗传到下一代的概率以及累积概率,最后使用轮盘赌算法,被选中的个体进入子代种群。例如,通过计算图2中4个个体的适应度值,根据式(2)得到每个个体的选择概率{0.56,0.12,0.87,0.24},适应度值越大,该个体被选择的概率也越大。
(2)
(3)
其中,L(xi)表示xi的累积概率,N表示种群的大小。
在选择操作完成后,GA对选择的个体进行交叉操作,如图3所示,本文使用随机多点交叉法,随机选择个体与另一个个体进行多点配对,并基因互换得到新个体。最后在个体中随机挑选一个或者多个基因位的基因值完成变异操作,如图4所示,其中,1表示保留特征,0表示舍弃特征。
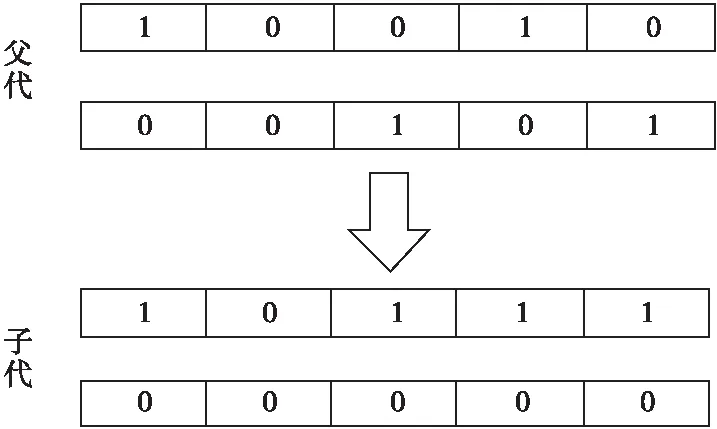
Figure 3 Random multipoint intersection
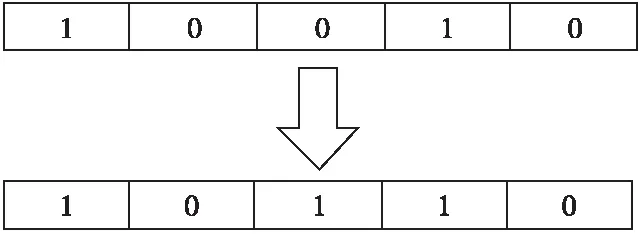
Figure 4 Gene mutation
(4)迭代终止。本文算法的迭代终止条件设置为100次。最终得到最优染色体。并通过该染色体确定其对应的最优特征。
3.1.2 CART算法的双层GA优化
遗传算法是全局优化算法,对于决策树模型来说,它能够找到最优的分裂点,取得最优的分类规则,从而进一步提升模型的分类精度。所以,本文利用双层遗传算法持续优化CART分类过程,以避免因CART算法中二分类过程所带来的局部最优风险。基于GA的CART双层优化主要是使用遗传算法替代二分法,从而找到决策树中的最优分叉点。根据基于GA的CART上层优化所得最优染色体,可以找到数据集的最优特征,即利用了较少的特征数据实现了高精度的样本分类。而在第2次遗传算法优化过程中,主要是针对经最优染色体选择后的特征进行权重赋值,然后利用同样的遗传算法更新特征权重,并根据特征权重选取最靠前的3个特征,最后基于所选择的3个备选分裂点进行建树分类,实现样本分类。
CART算法的双层GA优化过程的适应度值定义为决策树分类精度,如式(4)所示:
fitness_d(Dj)=acc_d(Dj)
(4)
其中,Dj表示数据集中的第j个特征,acc_d(Dj)表示利用第j个特征进行分类后的分类精度。
然后同样通过选择、交叉和变异操作,在决策树的第1层特征中迭代寻优,迭代完成之后输出最优的个体和最优的适应度值,算法终止。通过上述过程可以找到第1层的最优分裂点,之后每一层重复此操作便能生成决策树。
本文利用基于遗传算法的CART优化算法依据尝试次数、第1次响应和第1个动作等特性对数据进行预处理[20]。将基于遗传算法的决策树分类器与知识追踪模型DKVMN相结合,以提升底层模型对行为特征的处理能力。
3.2 交叉特征
通过预处理阶段,学生的行为响应特征被转化为决策树的响应,如图1所示,利用练习标签qt与决策树响应gt得到输入向量,它表示每个学生的练习以及练习时行为特征信息的输入,如式(1)所示:
c(qt,gt)=qt+max(q+1)*gt
(5)
其中,q表示最大练习数,qt表示学生t阶段的练习标签,gt表示学生的决策响应,即决策树预测的结果,c(qt,gt)表示练习及其决策响应的交叉特征。
3.3 相关权重
相关权重主要体现在注意力权重wt上,即使用嵌入向量kt来查询DKVMN模型中的Mk,查询结果是对每个知识点关注程度的加权,表示练习和每个潜在概念之间的相关性,这个注意力权重wt是求得Mk和kt的内积后借助softmax函数激活得到的,如式(6)~式(8)所示:
wt=softmax(Mkkt)
(6)
kt=c(qt,gt)×A
(7)
(8)
其中,静态矩阵Mk大小为N×dk,其存储的数据为潜在的概念信息,也就是整个知识空间中N个知识点的嵌入表示,每个行向量对应一个知识点的嵌入表示;kt为嵌入向量;A为嵌入矩阵。
3.4 读过程
读过程主要通过分析概念信息对答题情况进行概率预测,如式(9)~式(13)所示:
(9)
(10)
θt=tanh(wθft+bθ)
(11)
β=tanh(wβc(qt,gt)+bβ)
(12)
pt=σ(3.0×θt(j)-β(j))
(13)
其中,γt为学生对练习的掌握程度的总结;将阅读内容γt和输入的练习特征Kt连接起来,通过tanh激活来获得一个摘要向量ft,摘要向量内容包含学生对知识的掌握水平和问题的难度以及学习特征,矩阵W1和向量b1分别表示全连接层的权重与偏置;θt表示学生在t阶段对所有知识点的能力,β表示所有知识点的难度,知识点难度通过交叉特征c(qt,gt)的嵌入计算得出,即题目中的学生能力水平越高,其解决问题的能力越强,反之,学生能力水平越低,其解决问题的能力越弱;wθ和wβ分别表示学生能力和知识点难度的权重矩阵,bθ和bβ表示对应的偏置向量。σ(·)是sigmoid函数,本文将学生的能力扩大3倍,这样做是为了更加精确地预测,具体实验细节见4.4节。最后得到标量pt,即正确回答qt的概率。
3.5 写过程
根据艾宾浩斯遗忘曲线规律,人们对掌握的知识概念在一定的时段后会出现一定程度的遗忘。写过程主要是根据学生回答问题后,对答案的正确性进行更新值矩阵操作。先将(qt,rt)嵌入一个矩阵B中,以获得学生在完成本练习后的知识增长vt。写过程主要包括2个主要操作,即擦除内存和增加内存。擦除内存表示学生对知识概念遗忘的过程,如式(14)~式(16)所示:
et=sigmoid(ETvt+be)
(14)
(15)
(16)
其中,et表示擦除内存向量;E表示变换矩阵;be表示偏置向量;vt表示学生在完成本练习后的知识点增长;动态矩阵Mv大小为N×dv,每个行向量表示学生对于知识点的掌握情况。
增加内存表示学生通过练习和回答问题对相关概念的知识掌握的更新,如式(17)~式(19)所示:
at=tanh(DTvt+ba)T
(17)
(18)
(19)
其中,at是一个行向量,即增加内存向量,D表示变换矩阵,ba表示偏置向量。
这种先擦除后添加的机制符合学生在学习过程中遗忘和强化概念的知识变化状态。
4 实验
4.1 数据集
本文在3个公开数据集ASSIST2009[21]、ASSIST2012[21]和Algebra 2005-2006[22]上对知识追踪模型进行对比实验。数据集详情如表1所示。数据集ASSIST2009和ASSIST2012均来自ASSISTMENTS在线辅导系统,数据集Algebra 2005-2006来自KDD(Knowledge Discovery and Data mining)杯2010年教育数据挖掘挑战赛,其中分为开发数据集和挑战数据集,本文使用的是开发数据集。

Table 1 Statistics of datasets
(1)ASSIST2009。由于存在重复记录问题,官方发布了更新版本,本文使用更新后的版本进行实验。实验中的记录数量使用的是Zhang等人[3]处理后的数据,共计4 151名学生回答325 637个练习以及110个不同的练习标签。使用技能标签作为模型的输入。其中选择做题次数、第1次响应、第1个动作和尝试次数作为预处理阶段的特征输入。做题次数指学生完成一道题提交系统的次数。第1次响应指学生第1次响应的时间,单位为ms。第1次动作指学生第1次是否请求帮助。尝试次数指学生尝试练习的次数。
(2)ASSIST2012。由于该数据集较大,本文删除了记录数小于3的学生数据和技能标签为空的数据,并从中抽取5 000名学生信息,最终处理后的数据包括5 000名学生回答940 179个练习以及242个不同的练习标签,并用技能标签作为模型的输入。其中选择是否要求提示、第1次响应、第1次动作和尝试次数作为特征输入。是否要求提示指学生做题过程中是否要求所有提示。
(3)Algebra 2005-2006。此数据集是从卡内基学习平台收集的,包含574名学习者、210 527个练习标签和8 008 465次学习交互。本文选择提示响应、更正次数和机会次数作为特征输入。提示响应指学生为步骤请求的提示总数。更正次数指学生对该步骤的正确尝试次数,仅当多次遇到该步骤时才增加。机会次数指每次学生遇到具有所列KC的步骤时增加1次的计数。具有多个KC的步骤将有多个计数,由~~来分隔。
4.2 实验参数及评价指标
4.2.1 实验参数
模型中的学习率初始化为0.005,批处理大小为32,采用Adam优化器。此外,使用均值和标准偏差为0的高斯分布随机生成的方法对参数初始化。迭代次数设置为100。遗传算法中的参数设置如表2所示。

Table 2 Parameter settings in genetic algorithm
对于DKT模型,隐藏层大小从{10,50,100,200}中选择。对于DKVMN、Deep-IRT、DKVMN-DT以及DKVMN-GACART-IRT模型,静态键矩阵和动态值矩阵的维数也从{10,50,100,200}中选择。本文还从{5,10,20,50,100}中选择DKVMN、Deep-IRT、DKVMN-DT以及DKVMN-GACART-IRT模型的内存维度。为了减少参数数量,设置dk=dv。最后,在训练集上使用5重交叉验证法验证模型准确度,并在测试集上评估模型性能。
4.2.2 评价指标
本文使用AUC指标来对知识追踪模型的预测表现进行评估。AUC取值在0~1。其中AUC为0.5时表示其模型性能与随机猜测一样。AUC值越大,表示模型的性能越好。
4.3 实验结果与分析
本文将数据集划分为测试集、验证集和训练集3个部分,分别占30%,20%和70%,其中验证集从训练集中抽取得到。
参加比较的5个模型如下所示:
(1)DKT:以循环神经网络为基本结构,将隐藏状态解释为学生的知识状态。该模型成为知识追踪领域使用最广泛的模型之一。
(2)DKVMN:通过对MANN的改进,加入动态键值记忆矩阵来追踪学生的知识状态。
(3)Deep-IRT:以DKVMN为基础模型,将IRT与深度学习相结合。
(4)DKVMN-DT:将CART应用于DKVMN知识追踪模型预处理。
(5)DKVMN-GACART-IRT:将基于遗传算法的CART优化算法和IRT项目反应理论与DKVMN模型相结合,提高了模型的预处理能力和预测准确率。
因决策树对噪声数据的易敏感,在这3个数据集上DKVMN-GACART-IRT和DKVMN-DT均出现了过拟合现象,通过剪枝后的实验数据如图5~图7所示。
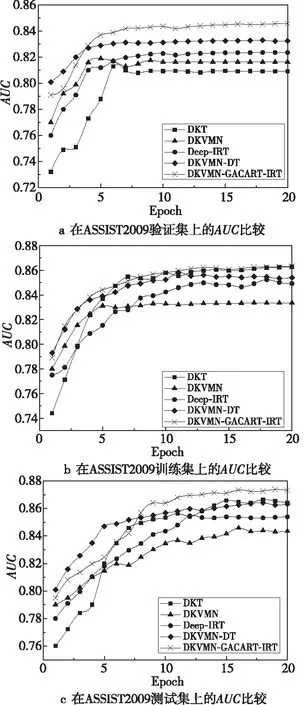
Figure 5 AUC comparison on ASSIST2009 dataset
4.3.1 ASSIST2009实验结果
从ASSIST2009数据集中抽取30%数据组成测试集,其余70%数据组成训练集,从训练集中抽取20%数据组成验证集,比较各个模型在该数据集上的AUC表现。如图5a所示,DKVMN-GACART-IRT模型的AUC相比其他模型的虽无明显提升,但曲率平滑,具有较好的稳定性。而在训练集上,如图5b所示,DKVMN-GACART-IRT模型随着迭代次数的增加AUC表现较好。如图5c所示,DKVMN-GACART-IRT模型的AUC表现稳定并与其他原始模型的相比有略微的优势。
4.3.2 ASSIST2012实验结果
从ASSIST2012数据集中抽取30%数据组成测试集,70%数据组成训练集,从训练集中抽取20%数据组成验证集,比较各个模型在该数据集上的AUC表现。如图6a所示,由于该数据集较大,所有对比模型前7轮迭代情况相近,而随着迭代次数的增加,Deep-IRT模型与DKVMN模型的AUC表现相近,而DKVMN-GACART-IRT模型的AUC为77.08%,优于其他模型的。在训练集上,如图6b所示,DKVMN-GACART-IRT模型的AUC比Deep-IRT模型的高出3.1%、较DKVMN-DT模型的高出1.2%。如图6c所示,DKVMN-GACART-IRT模型呈现出较大优势,比DKVMN-DT模型的AUC高出1.48%,比DKVMN模型的AUC高出2.53%。
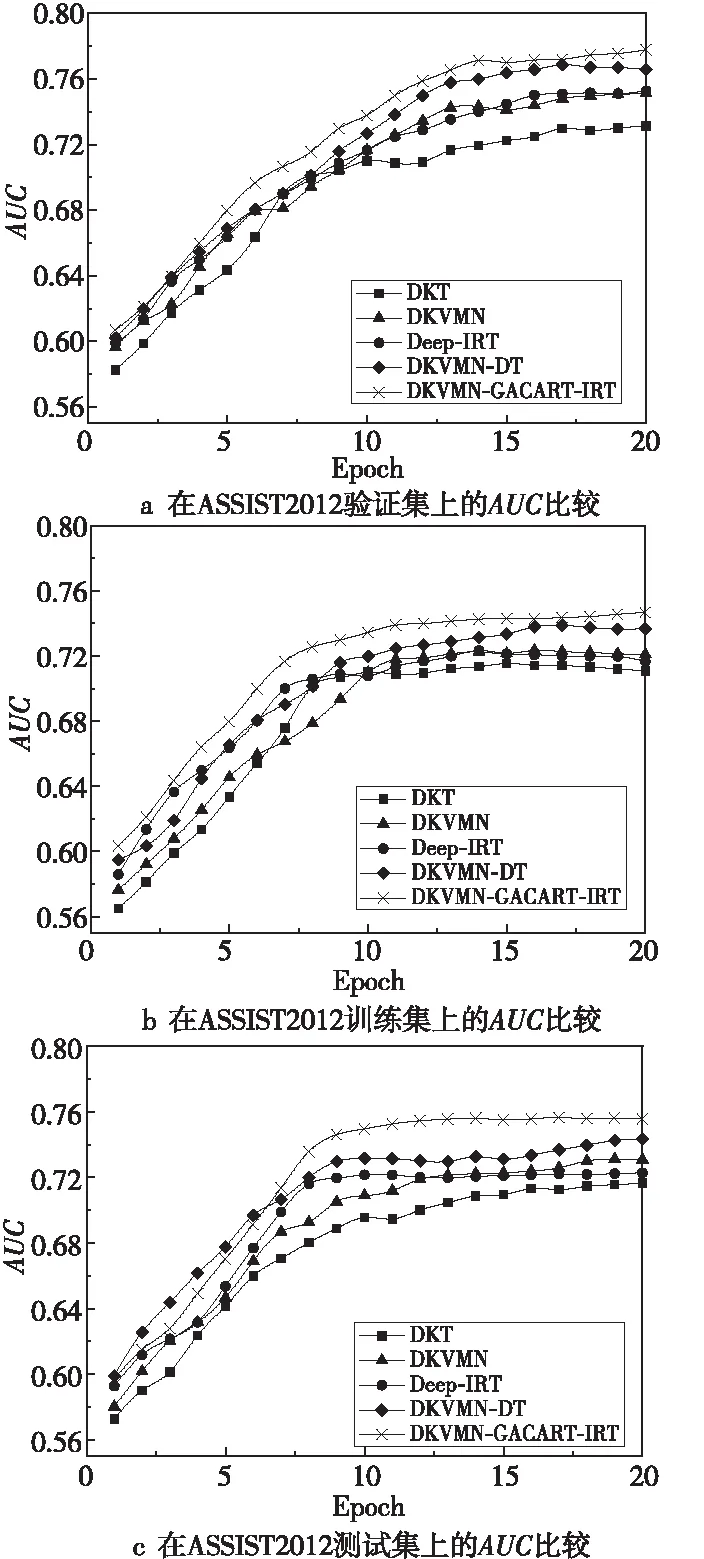
Figure 6 AUC comparison on ASSIST2012 dataset
4.3.3 Algebra2005-2006实验结果
从Algebra 2005-2006数据集中抽取30%数据组成测试集,其余70%数据组成训练集,从训练集中抽取20%数据组成验证集,比较各个模型在该数据集上的AUC表现。如图7a所示,DKVMN-DT模型的AUC表现更好,而DKVMN-GACART-IRT模型与DKVMN-DT模型均优于其他模型。在训练集上,如图7b所示,DKVMN-GACART-IRT模型的AUC比Deep-IRT模型的高出3.8%、较DKVMN-DT模型的高出0.7%。如图7c所示,DKVMN-GACART-IRT模型与DKVMN-DT模型具有相似的AUC性能,且都高于其他模型的AUC,但DKVMN-GACART-IRT具有更好的稳定性。
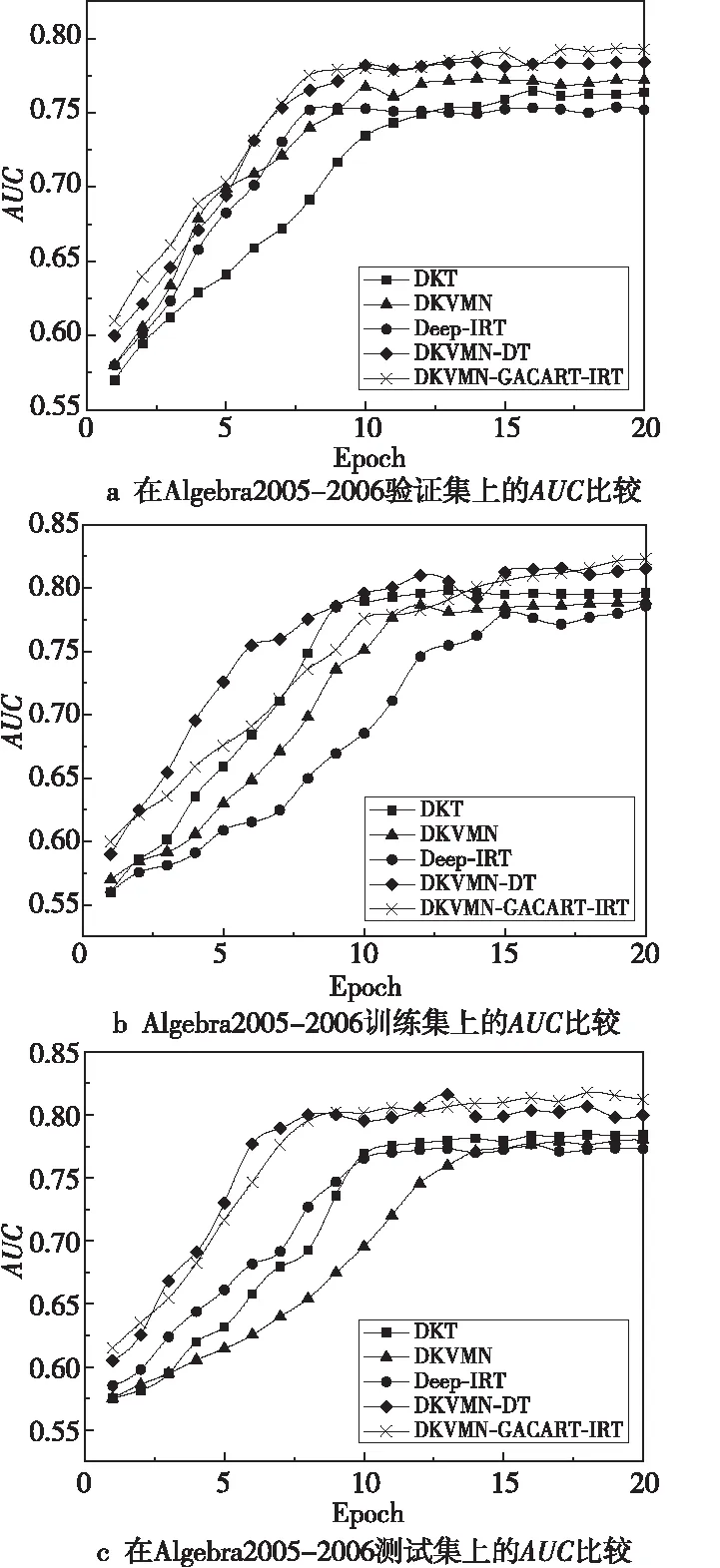
Figure 7 AUC comparison on Algebra2005-2006 dataset
DKVMN-GACART-IRT与经典模型DKT、DKVMN、Deep-IRT和DKVMN-DT的对比实验结果如表3所示,可以看出,本文的DKVMN-GACART-IRT模型在ASSIST2009数据集上的AUC性能指标高达84.57±0.08,而作为基线的DKVMN模型的AUC达到81.63±0.07。DKVMN-DT模型的AUC达到83.23±0.1。DKVMN-GACART-IRT的AUC比DKVMN的高出2.84%,比DKVMN-DT的AUC高出1.34%。在ASSIST2012数据集上,本文模型的AUC达到77.01±0.06,比DKVMN的AUC高出3.9%,比Deep-IRT的AUC高出3.37%。而相较于DKVMN-DT模型的AUC高出1.99%。在Algebra2005-2006数据集上,DKVMN-GACART-IRT模型的AUC达到78.66±0.12。而DKVMN模型的AUC达到77.36±0.12,DKVMN-DT模型的AUC达到78.42±0.1。DKVMN-GACART-IRT的AUC比DKVMN的高出1.3%,比DKVMN-DT的高出0.24%。从以上数据可以客观得出,本文所提出的DKVMN-GACART-IRT模型在3个公开数据集上均优于DKT模型、DKVMN模型、Deep-IRT模型及DKVMN-DT模型,表明本文所提出的DKVMN-GACART-IRT模型通过对学习者行为特征的预处理以及加入心理测量学IRT模型,提升了预测性能。

Table 3 AUC comparison of DKT,DKVMN,Deep-IRT,DKVMN-DT and DKVMN-GACART-IRT
4.3.4 消融实验
本文模型包括基于GA的CART预处理模块和心理测量学模块2个主要部分,为了分析不同部分对知识追踪预测性能的影响。本节在ASSIST2009数据集上进行消融实验。本节设置以DKVMN为底层模型,与分别加入基于GA的CART预处理模块和心理测量学IRT模型进行对比实验,分析2个模块对预测性能的影响,在ASSIST2009数据集的上实验结果如表4所示。从表4可以看出,相较于DKVMN基线模型,加入基于GA的CART预处理模块和心理测量学IRT模型的预测准确率都有一定提升。通过心理测量学IRT模型,增加底层模型读操作中的可解释性,预测准确率相较于DKVMN基线网络有大约0.14%的提升。基于GA的CART预处理通过对学习者的不同行为特征进行分析,将预处理后的行为特征与学习特征交叉,相较于基线模型有 1.69%的提升。基于GA的CART预处理与心理测量学IRT模型的共同作用相较于基线模型提高了3.01%的准确率,说明本文模型在预测性能上更优。

Table 4 Ablation experimental results on ASSIST2009 dataset
4.4 参数解析
本文3.4节中,在对学生答题情况进行概率预测时,将学生的能力扩大3倍,如式(13)所示,θtj的取值为(-1,1),βj的取值为(-1,1)。为了得到更加精确的预测,本节针对不同扩大倍数的学习能力在ASSIST2009数据集上进行实验。在实验中设置学习最小能力θtj≈-1,习题最大难度βj≈1,使pt逼近于0。设置学习最大能力θtj≈1,习题最小难度βj≈-1,使pt逼近于1。
实验结果如表5所示。当学习能力扩大倍数为1时,预测最小概率pt≈0.119,最大概率pt≈0.881,AUC值为81.937%。当学习能力扩大倍数为2时,预测最小概率pt≈0.0474,最大概率pt≈0.953,AUC值为83.328%。从表5的结果中可以看出,pt的取值范围过小。一方面,pt归缩范围较窄,不符合模型预测范围;另一方面,这会导致预测结果模糊,使不同学生的学习能力无法精确拉开差距。

Table 5 Experiment of the expansion of learning ability
当学习能力扩大倍数为4时,预测最小概率pt≈0.0067,最大概率pt≈0.993,AUC值为82.965%。从表5的结果中可以看出,pt的取值范围过大。原因有2个方面:一方面,学习能力是动态变化的,当学生学习能力产生微弱波动时,在较大倍数作用下会导致预测结果发生很大改变;另一方面,学生答题过程中难免会出现猜测和失误的情况,参数倍数过大也会使结果与实际产生较大偏差。这些都会造成预测结果不精确。
综上所述,本文通过针对学习能力扩大不同倍数的实验后,在式(13)中使用扩大3倍的学习能力,使预测结果更加精确。
5 结束语
本文针对行为特征预处理对整个模型的影响,提出了一个将基于遗传算法的CART优化算法与Deep-IRT相结合的优化模型。该模型通过GA-CART决策树对学习者的行为特征进行预处理,即对特征信息分类筛选后再将特征向量融合到DKVMN底层模型中,而在DKVMN的读过程中加入了IRT项目反应理论,保留了DKVMN模型的性能,同时能够评估KC难度和学生的能力水平。本文所提出的DKVMN-GACART-IRT模型在3个数据集上分别与DKT、DKVMN、Deep-IRT和DKVMN-DT进行了对比实验,在预测的预处理阶段和读过程中,既提升了预测性能又保留了对难度水平和学生能力的分析,也表明了本文模型在公开数据集上的有效性和可解释性。在未来的工作中作者将从2个方向进一步开展研究:一方面,将不同年龄或者领域的学习者用户画像与知识追踪相融合;另一方面根据教育心理学中的成败归因论,通过分析学习者的动态心理状态提高模型预测能力。
