融入重心反向学习和单纯形搜索的粒子群优化算法

张文宁,周清雷,焦重阳,梅 亮

(1.信息工程大学数学工程与先进计算国家重点实验室,河南 郑州450001;2.中原工学院软件学院,河南 郑州 450007;3.郑州大学信息工程学院,河南 郑州 450001)

1 引言

粒子群优化PSO(Particle Swarm Optimization)[1]算法因其易理解、参数少等优点受到研究人员的关注并得以广泛应用,但存在群体多样性下降迅速、易早熟收敛、全局寻优和局部寻优能力难以平衡等问题。为此,人们开展了参数及拓扑结构优化[2]、学习模式改进以及与其他智能优化算法融合等方面的研究[3]。

在学习模式改进方面,反向学习已成为提升粒子群优化算法性能的常用有效策略之一[4]。Wang等[5]首次将反向学习引入粒子群优化算法;周新宇等[6]提出了精英反向学习模型来提升对精英解的开发能力;喻飞等[7]提出了透镜成像反向学习策略的粒子群算法;邵鹏等[8]基于折射原理提出反向学习的统一模型。然而,已有研究工作大多基于变量所在维度的取值上限及下限计算反向个体,缺少对群体搜索经验的充分利用。

Rahnamayan等[9]提出基于种群的重心反向学习策略,并将其应用于差分进化算法。周凌云等[10]以邻域重心为参考,利用不同邻域的搜索经验保持粒子种群的多样性。罗强等[11]在粒子进化中引入对全局最优粒子的逐维重心反向学习变异策略,降低了维度间的干扰。这些方法选用种群内的所有个体或历史最优个体反向学习,忽略了个体与最优个体的关联关系,造成了一定的计算资源浪费。

受重心反向学习[9]启发,本文提出基于选择性重心反向学习和单纯形搜索的粒子群优化COLS-PSO(Centroid Opposition based Learning and Simplex search PSO)算法。首先,在混沌初始化基础上,计算个体与最优个体关联关系;然后,选择需要反向学习的个体,避免计算资源消耗,提高种群变异能力;进一步提出局部单纯性搜索方法,通过反射和扩张操作探索有益优化方向,增强对最优解邻近区域的局部开发能力,以提高搜索精度。

2 粒子群优化算法分析

2.1 粒子群优化算法

(1)

(2)

(3)

其中,c1和c2为学习因子,r1和r2为0～1的随机数,wt为随迭代过程线性递减的惯性权重,wmax和wmin分别为惯性权重最大值和最小值,t表示当前迭代次数,T表示最大迭代次数。

2.2 粒子个体行为分析

在一维连续空间中,粒子在单位时间内的位置更新过程可通过合并式(1)和式(2)得到简化的粒子更新方程,这样不仅可以减小速度项参数的影响,还可以降低算法的难度,如式(4)所示[12]：

(4)

进一步,令φ1=c1r1,φ2=c2r2,φ=φ1+φ2,则粒子在一维空间中的位置变化过程可用式(5)所示的二阶微分方程来表示:

(5)

根据李亚普诺夫意义下对离散时间系统稳定性判定的分析可知,粒子群优化算法在wt<1,φ>0,2wt-φ+2>0取值范围内,粒子保持正弦运动轨迹。

2.3 粒子群体行为分析

粒子群体具备正向反馈的增强学习机制,遵循择优保留策略,前期收敛速度较快,后期收敛速度较慢。若粒子位置的更新过程按其期望值进行观察,胡旺等[12]通过严格的数学推导证明了粒子群优化算法在参数满足稳定性条件下将收敛于p*,如式(6)所示:

(6)

3 改进粒子群优化算法COLS-PSO

3.1 混沌初始化

从粒子个体行为分析可以看出,单个粒子的运动轨迹由初始位置和初始速度决定。相比于随机初始化方法,基于混沌序列生成的初始化种群有更好的多样性,有助于算法在进化初期探索尽可能广的搜索空间。

本文采用Logistic映射,按照式(7)产生混沌序列,并根据式(8)将其映射到搜索空间。

(7)

xid=Ld+chk*(Ud-Ld)

(8)

式(7)中,k表示迭代时间步,chk表示第k次混沌演化后的取值,rand()表示0～1的随机数,α表示控制参数,一般取值为4;式(8)中,xid表示混沌序列映射到搜索空间中第d维的位置,Ud和Ld分别表示第d维搜索空间的取值上界和下界。

种群规模为30时,种群的随机初始化和混沌初始化在二维空间中的个体分布如图1所示。从图1可以看出,混沌初始化相较于全随机初始化有较好的分散性,为初始搜索的良好探索能力奠定了基础。

Figure 1 Initial population

采用混沌策略生成初始种群的具体操作步骤如算法1所示。

算法1采用混沌策略生成初始化种群

输入：种群规模N,搜索空间维度D,D维搜索空间的取值下界L和上界U。

输出：N个粒子组成的初始种群。

步骤1随机生成D个0～1的随机数,作为Logistic映射的初始取值。

步骤2根据每个维度的搜索空间取值上下界,基于式(8)生成D个维度的位置坐标,形成初始种群内第1个粒子的位置X0。

步骤3逐个生成N个粒子的位置,形成初始种群。

步骤3.1对D个Logistic映射的初始取值,基于式(7)进行混沌演化,生成新的D个混沌演化值。

步骤3.2基于式(8)将混沌演化值映射为第2个粒子的位置。

步骤3.3以此类推,每进行一次混沌演化,都可以将其映射为一个粒子的位置。

3.2 选择性重心反向学习

(9)

(10)

Spearman相关系数用于衡量2个随机变量的依赖程度,对原始变量的分布特性无要求,具有较强的适应性。

2个D维随机变量Xi=(xi1,xi2,…,xiD)和Xj=(xj1,xj2,…,xjD) 的Spearman相关系数定义如式(11)所示:

(11)

其中,di表示Xi和Xj的等级差。等级是将D维随机变量的所有值从小到大排序后形成的等级,依次为1,2,…,D,如d1表示xi1和xj1在各自排序后所处等级的等级差。rs的取值在[-1,1]。rs>0表明2个随机变量正相关,其变化方向相同;rs<0表明2个随机变量负相关,其进化方向相反;rs=0表明两者不相关。

将Spearman相关系数应用于粒子群优化算法时,采用Spearman相关系数度量个体与gbest的关系,选择那些与gbest相关系数不大于0的个体进行反向学习。对于原个体及其重心反向学习后的个体,通过比较2个粒子的适应度函数值进行贪婪选择,将其中的优秀个体作为参与下一代进化的粒子,以提高种群变异能力。

3.3 局部单纯形搜索

作为一种典型的局部搜索方法,单纯形法SM(Simplex Method)通过构造n维单纯体空间并采用反射、扩展和压缩等操作改善个体质量[13]。近年来,研究人员常将其与全局寻优算法相结合,多数研究成果通过运用单纯形搜索方法改善较差个体,以提升种群质量,但较少用于精英解质量的提升。

为了加强最优个体邻近区域的开发,本文提出一种改进的局部单纯形搜索方法,其步骤如下所示:

输入：粒子种群。

输出：群体最优位置Xbest。

步骤1确定粒子种群中的最优个体位置Xbest、次优个体位置Xbetter和第3优个体位置Xgood,按照式(12)计算Xbest和Xbetter的重心Xcenter：

Xcenter=(Xbest+Xbetter)/2

(12)

步骤2按照式(13)对Xgood进行反射,生成反射个体Xreflection：

Xreflection=Xcenter+α′(Xcenter-Xworst)

(13)

其中α′为反射系数,取值为1。

步骤3如果Xreflection优于Xbest,则进一步按照式(14)进行扩张,生成扩张个体位置Xexpansion：

Xexpansion=Xcenter+γ(Xreflection-Xcenter)

(14)

其中γ为扩张系数,取值为2。若Xexpansion优于Xbest,则用Xexpansion代替Xbest,否则用Xreflection代替Xbest。

该方法以粒子群优化算法优化结果作为单纯形搜索的输入,以单纯形搜索指导最优粒子的搜索方向。优化过程中将种群内质量最好的前3个粒子位置组成初始单纯形,形成小型搜索空间,然后执行反射和扩张,在单纯形搜索结束后采用贪心策略选择和保留优秀个体位置。

为验证局部单纯性搜索方法对粒子群优化算法最优解的有效性,以Sphere函数为例,观察在不同种群规模和不同维度下单纯形搜索对种群最优解的平均改进次数,结果如表1所示。从表1可以看出,局部单纯形搜索方法能较为稳定地发挥其对最优粒子的开发能力。

Table 1 Efficiency of local SM

单纯形搜索方法无需考虑优化目标的梯度信息,仅通过目标函数值比较就可进行多点信息搜索。如果全部个体参与单纯形搜索,则需要很长时间才能进行个体质量的改善。如果组成初始单纯形的顶点为粒子群的优秀解,则可以在不增加算法复杂度的情况下,集中精英解的搜索经验,强化算法对潜在区域的开发。从搜索步骤来看,反射使得第3优粒子向重心反方向搜索,在进化方向正确的情况下,进一步向距离第3优粒子更远的方向扩展,以提高最优解的质量。粒子群优化算法全局搜索能力与单纯形的局部搜索方法有较强的互补性,两者的结合能丰富算法的搜索方向。

3.4 COLS-PSO算法

具备重心反向学习和单纯形搜索的粒子群优化算法如算法2所示。

算法2COLS-PSO算法

输入：种群规模N,搜索空间维度D,最大迭代次数T,惯性权重wmax和wmin,学习因子c1和c2,重心反向概率p。

输出：种群最优解。

步骤1利用算法1,基于Logistic混沌映射产生规模为N的初始化种群并计算相应的适应度值。

步骤2种群最优值gbest初始化为种群最优粒子位置。

步骤3根据式(4)更新每个粒子在每个维度的位置。

步骤4更新pbest和gbest。

步骤5对寻优的每一代执行以下操作:

步骤5.1产生一个随机数rand;

步骤5.2若随机数rand小于反向学习概率p：

步骤5.2.1按照式(9)计算种群重心M;

步骤5.2.2计算粒子与gbest关联系数rs;

步骤5.2.3若rs≤0,则按照式(10)产生反向个体;

步骤5.2.4贪心选择粒子或反向个体进入下一代;

步骤5.3采用单纯形方法对gbest深度开发。

4 数值实验与分析

4.1 算法及参数设置

本文选取与改进相关的若干有代表性的算法进行比对。这些算法分别为基于惯性权重线性调整的标准粒子群优化SPSO(Standard Particle Swarm Optimization)算法、采用约简粒子群优化算法并对权重进行自适应调整的RAPSO(Reduced Adaptive Particle Swarm Optimization)、基于邻域重心反向学习变异策略的NCOPSO(Neighborhood Centroid Opposition based Particle Swarm Optimization)、使用混沌策略的混沌粒子群优化CSPSO(Chaotic Search Particle Swarm Optimization)算法和引入单纯形搜索的单纯形粒子群优化NM-PSO(Nelder-Mead based Particle Swarm Optimization)算法。以上算法均涉及多种优化策略,算法参数尽量与原文保持一致,COLS-PSO中的参数与传统粒子群优化算法保持一致,重心反向学习概率参考NCOPSO等的研究结果,取值为0.3,算法具体参数设置如表2所示。

Table 2 Parameters setting of algorithms for comparison

4.2 测试函数

本文采用常见的基准测试函数对算法的寻优能力进行评价。其中,f1～f4为常用单峰函数,分别为Sphere、Rosenbrock、Duadric和Powersum函数,一般用来检验算法的收敛速度和求解精度;f5～f8为常用多峰函数,分别为Griewank、Rastrigin、Schwefel和Acley函数,用于评估算法跳出局部极值的全局搜索能力;f9～f10为CEC’2013中的偏移单峰函数,f11和f12为CEC’2013中的偏移多峰函数,用于评估算法在更复杂的最优解偏移(非0值)情况下的寻优精度。

本文选取参考文献中较为严格的实验参数,如表3和表4所示,4列分别表示测试函数(Function)、取值范围(Range)、最优解(Opt)和目标精度(Goal)等。

Table 3 Benchmark test functions

Table 4 CEC’2013 test functions

本文利用6种算法分别对表3和表4中的常见基准测试函数和CEC’2013中的偏移测试函数进行测试,以验证算法的寻优性能。为公平起见,设定所有算法运行的终止条件为达到150次的最大迭代次数。执行环境为Intel i7 CPU 2.6 GHz.RAM 8 GB,Windows 10 操作系统,Anaconda3。实验结果取20次独立运行的平均值,结果如表5和表6所示。

Table 5 Average optimization results of test functions(N=20,D=30)

Table 6 Average optimization results of test functions(N=30,D=100)

4.3 求解精度

从表5函数平均优化结果来看,在单峰测试函数求解中,COLS-PSO在测试函数f1和f2上均得到了精度最高的解;在测试函数f3上,RAPSO、NM-PSO和COLS-PSO取得最优解精度的数量级相同,其中COLS-PSO最优解质量略低于RAPSO找到的最优解;在测试函数f4上,NM-PSO取得最高精度的解;在多峰测试函数的求解中,f5测试函数的变量关系复杂,f6测试函数中存在大量局部极值,但NCOPSO和COLS-PSO都能找到最优解,显示了较好的跳出局部极值的能力;测试函数f7是连续平滑多峰函数,存在很深且远离全局最优的局部极值,COLS-PSO解的精度高于其他算法,显现了良好的突变能力;测试函数f8存在多种寻优方向,维度越大寻优方向越多,NCOPSO解的质量高于其他算法,COLS-POS解的质量略差于NCOPOS;在偏移测试函数的求解中,各算法在偏移单峰测试函数f9和f10上的寻优精度明显下降,原因在于PSO在求解最优解为0的优化问题时性能较好,求解最优解偏离0的优化问题时性能有所下降,即偏移函数中最优解的偏移加大了寻优难度。相比较而言,NCOPSO和COLS-PSO采用重心反向学习机制以种群的几何重心为参考对种群进行变异,受坐标搜索偏向的影响较小,这使得两者的寻优精度在f9和f10上优于其他算法的。f11和f12均为解空间复杂的偏移多峰测试函数,NCOPSO和COLS-PSO略优于其他算法,但整体上各算法的寻优精度差别不大。

从表6可以看出,在维度为100的情况下,COLS-PSO能在f1、f2、f3和f7上取得最优结果,NCOPSO和COLS-PSO在f5和f6上均能找到最优解,COLS-PSO在高维度优化函数上性能较好。结合表5和表6的数据进行综合分析可以发现,NCOPSO在维度提升时解的精度没有受到太大影响。

以上实验结果表明,COLS-PSO在求解优化函数时表现出了较好的稳定性和良好的寻优能力。主要原因是简化的粒子群优化算法一定程度上加快了算法收敛速度,重心反向学习策略能在充分利用群体经验的情况下帮助粒子跳出局部最优解,同时增强的局部开发能力进一步提高了算法的收敛精度。

4.4 收敛曲线

算法收敛速度直接决定了算法的可用性和实用性,是衡量算法性能的重要指标。在种群规模为20、变量维度为30的条件下,每个测试函数在给定最大迭代次数情况下能达到的适应度情况如图2所示,横坐标为迭代次数,纵坐标为函数适应度值的对数函数值lg(f(x))。为防止纵坐标范围过大,限定函数适应度的最小值为10-15,即纵坐标的最小值为-15,纵坐标的最大值由各优化函数的适应度值自行采用合适的范围。

Figure 2 Fitness evolutionary curves of functions

从图2中各测试函数的收敛曲线来看,COLS-PSO和NCOPSO相较于其他算法来说,在大部分函数上具有较快的收敛速度;单峰测试函数的求解过程中,在测试函数f1上,COLS-PSO收敛曲线快速下降,RAPSO和NCOPSO收敛速度相当,体现了简化粒子群优化算法的正确性和高效性;在测试函数f2上,COLS-PSO快速收敛,RAPSO收敛速度稍有缓慢,NM-PSO收敛速度次之,NCOPSO收敛速度不太理想,但高于CSPSO和SPSO;在测试函数f3和f4上,RAPSO、NCOPSO、COLS-PSO和NM-PSO等的收敛曲线均能快速下降,体现了重心反向学习策略较好利用群体搜索经验的能力以及单纯形搜索良好的局部开发能力;多峰测试函数的求解过程中,在测试函数f5和f6上,NCOPSO和COLS-PSO收敛速度明显快于其他算法的,RAPSO和NM-PSO收敛曲线较为一致,体现了较好的跳出局部极值能力;在测试函数f7上,COLS-PSO具有最快收敛速度,体现了算法进行选择性重心反向学习的较强极值扰动性能,NCOPSO算法在该测试函数上的搜索空间略显不足,容易陷入局部极值;在测试函数f8上,NCOPSO收敛曲线下降速度最快,高于其他算法。

综上,对于精度要求不高的连续优化问题,COLS-PSO能够取得最佳的收敛速度。究其原因,在于COLS-PSO在迭代过程中对最优解进行的增强式局部学习、较强的全局搜索和局部搜索间的平衡能力,在保持种群多样性的同时提高了算法的求解精度。除f8函数外,COLS-PSO都能以最快的速度收敛,说明了该算法的正确性和高效性。

4.5 有效性

算法有效性通过达到目标精度的运行次数占实验总次数的比例(成功率)表示。根据表3中测试函数设定的取值范围及目标精度,部分优化函数在20次独立运行过程中达到目标精度的迭代统计数据如表7所示。

Table 7 Number of iterations for the goal of benchmark functions

从表7可以看出,SPSO对所有优化函数均未能在150次迭代内达到预定精度。结合图2来看,SPSO的收敛曲线平稳,收敛速度慢;在单峰测试函数f1、f2和f4上,RAPSO和COLS-PSO均能以较少迭代次数达到目标精度,NCOPSO除f2外均能达到目标精度;在多峰测试函数方面,除测试函数f7外,NCOPSO和COLS-PSO均能在迭代次数内达到目标精度,其中NCOPSO在测试函数f8上的平均迭代次数低于COLS-PSO,COLS-PSO在f6和f7测试函数上达到目标精度所需平均迭代次数最小;从平均迭代次数上看,COLS-PSO所需要的平均迭代次数在17～45次,表明COLS-PSO能在较低迭代次数内满足实验要求,有较高的实用价值。

4.6 时间复杂度

假设种群规模为N,搜索空间维度为D,最大迭代次数为T,COLS-PSO迭代过程中更新个体位置的时间复杂度为O(ND),种群进行重心反向学习改变了学习对象但并未增加时间开销,时间复杂度为O(ND),对最优解开展局部学习的时间复杂度为O(D)。由此,整体时间复杂度为O(T*(2ND+D)),略去低阶项后的时间复杂度为O(TND)。

标准粒子群优化算法迭代优化部分的时间复杂度为O(TND)。RAPSO基于粒子和种群平均适应度值为个体赋予不同惯性权重,其迭代部分的时间复杂度为O(T*(N+ND))。CSPSO采用混沌策略加强对个体局部开发能力,相应的时间复杂度为O(T*(ND+D))。NCOPSO需要持续更新粒子邻居矩阵,其时间复杂度为O(T(4ND+N2))。NM-PSO中每个粒子受其他随机粒子吸引合力的影响,其迭代部分的时间复杂度为O(T(3ND+N2D))。

综上所述,COLS-PSO算法的时间复杂度优于NCOPSO和NM-PSO的,与RAPSO和CSPSO的相当,次于标准粒子群优化算法的。

4.7 收敛性分析

王晖[16]证明了一般反向学习群体搜索算法的收敛性,本文基于其结论对COLS-PSO收敛性作简要证明。

定理1若基于一般反向学习的PSO算法收敛,则COLS-PSO算法也是收敛的。

(15)

根据式(9)产生的种群重心M在第d维的变量Md,有:

(16)

当t→∞时,根据式(10)重心反向学习产生的反向个体的收敛情况如式(17)所示:

(17)

综上,当粒子收敛于Xbest时其重心反向学习产生的反向解也收敛于Xbest。因此,基于一般反向学习的PSO收敛,则COLS-PSO也是收敛的。

□

5 应用于测试数据生成问题

5.1 实验设置

为测试算法在测试数据自动生成方面的表现,本节选取若干基准测试程序进行测试,如表8所示。选取的目标路径为程序中较难覆盖的路径,判定条件较为严格。实验中相关参数保持一致,最大迭代次数为500,种群规模为50,执行环境为Intel i7 CPU 2.6 GHz.RAM 8 GB,Windows 10 操作系统,Anaconda3。

Table 8 Benchmark test programs

5.2 实验结果分析

在算法的评价指标方面,本文选取找到目标解的迭代次数及其成功率进行度量。在种群规模为50的情况下,对于每个被测源程序,分别统计算法找到满足目标路径所需测试数据的最小迭代次数、最大迭代次数、平均迭代次数和成功率。实验结果取20次独立运行的平均值,具体如表9所示。

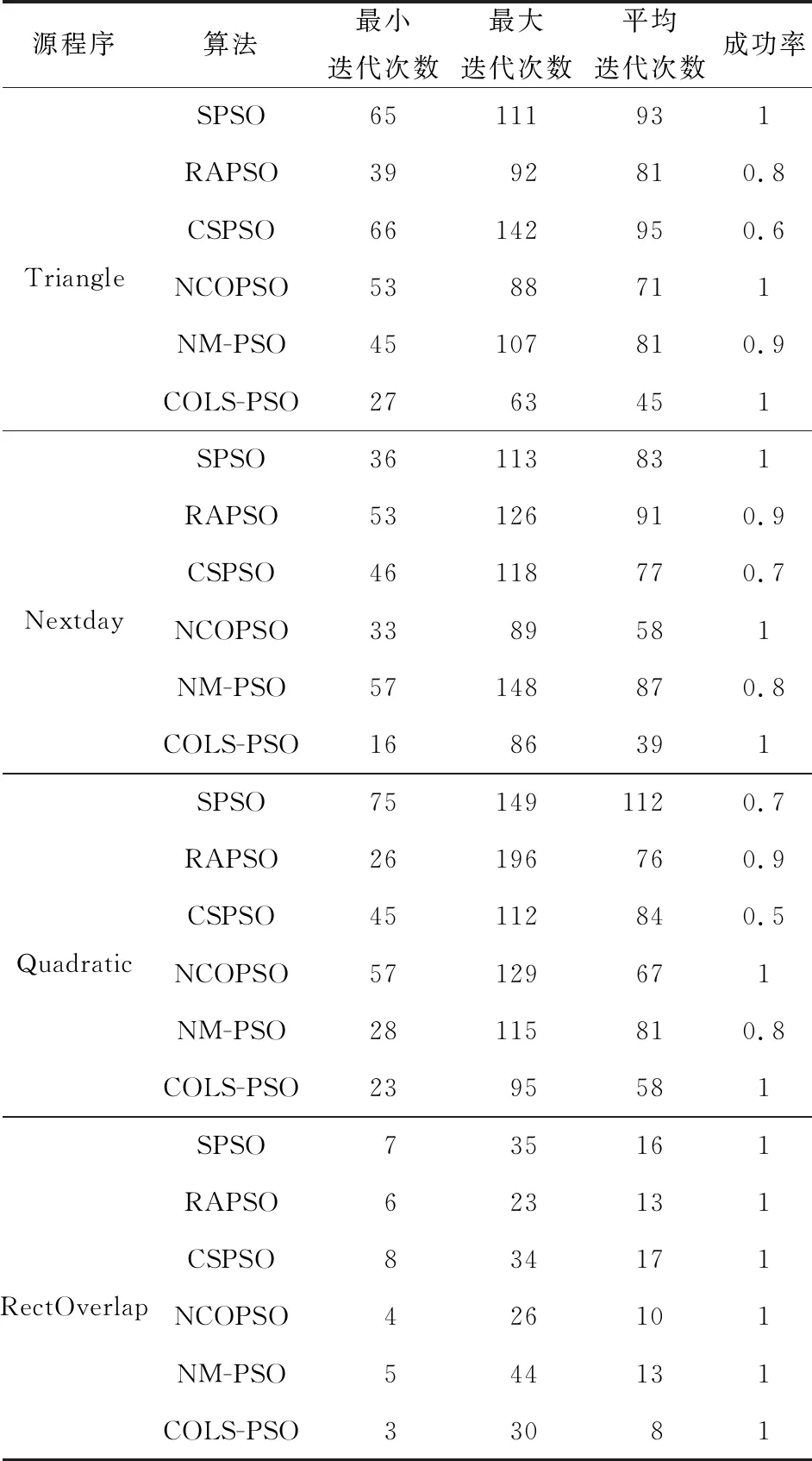
Table 9 Iterations for benchmark programs

从表9数据可以看出,在RectOverlap测试程序中,所有算法都能以较少迭代次数找到测试数据,原因在于参数保留小数后2位的机制提高了矩形交叉的概率;在Triangle、Nextday和Quadratic程序中,NCOPSO和COLS-PSO算法均能找到目标测试数据。相对来说,SPSO和CSPSO的收敛迭代次数较大,RAPSO除在Nextday程序中收敛迭代次数较大外,在其余3个程序上收敛迭代次数较小,NCOPSO和COLS-PSO收敛迭代次数最小,表现出了良好的稳定性。

6 结束语

本文提出具有选择性重心反向学习和单纯形搜索的COLS-PSO算法。初始时,基于Logistic映射产生混沌序列生成个体初始位置。进化过程中群体以一定概率进行重心反向学习,以便跳出局部极值。根据Spearman相关系数选择部分粒子进行重心反向学习,在不增加时间复杂度的情况下改变粒子运动轨迹。还进一步通过局部单纯形搜索增强对最优粒子潜在区域的开发,提高搜索精度。实验结果表明,所采用的策略能够提高算法的寻优性能。

本文所提COLS-PSO算法可以较为方便地应用到其他智能算法的优化中,后续将探索其在测试数据生成求解问题中的优化策略,并与其他智能优化算法相结合展开研究。