基于遗传算法的两阶段应急物流配送中心选址研究

程元栋,闫 俊,杨齐威

(安徽理工大学 经济与管理学院,安徽 淮南 232000)

近年来,我国地震、旱涝、公共卫生事件等各种自然灾害频频发生,给社会发展和人民生命财产带来了巨大损失。而应急事件具有突发性的特性,救援活动环节复杂且物资来源广泛,因此为避免灾害进一步的扩大,在灾后及时制定合理有效的物流配送中心选址及配送路径方案,具有重要理论意义和实践价值。

目前众多国内外科学家对应急物流选址问题做了大量研究。Hakimi S. L[1]最先对选址问题进行探讨,随后很多学者对其进行不断的深入研究,逐渐完善成理论体系。其中郭鹏辉[2]等针对灾害发生后资源受限的情况下,建立了以运输时间最短、各个需求点的综合满意度最大以及满足度差异最小为目标的应急物流选址-路径-配给优化模型。郑琰[3]等针对城市应急物流选址问题,建立了考虑覆盖率、总时间成本的多目标0～1整数模型,并利用深度优先搜索法和模糊神经网络法进行求解。以上的研究往往直接采用模型进行问题求解,却忽略了宏观因素对选址问题的影响,因此,部分学者采用因素评价法与算法相结合进行选址研究。其中Trivedi A、Singh A[4]提出一种综合运用层次分析法、模糊综合分析法和目标规划法的一种混合算法进行物流选址设施问题的研究。姚红云、牛凯[5]将选址与路径问题结合研究,构建了基于模糊层次分析法的算法模型,通过案例仿真证明了模型的可靠性。倪卫红[6]构建了考虑受灾地区受灾程度、地理坐标、需求量以及成本等多个目标,并采用聚类-重心法求解的应急物流配送中心选址模型。上述文献在构建模型时,通常只对成本目标进行优化,却未满足应急物流中对物资时效性的要求。针对此问题,部分学者在模型中引入时间窗约束以提高整体物资配送效率。赵建有等[7]构建了时间窗、物资需求紧迫度、载重约束下考虑总运输成本最小化的应急物流选址模型,并采用遗传算法对模型进行求解。杨郑[8]根据受灾情况构建了需求紧迫度评价体系并以此对配送车辆时间窗进行了调整,结合遗传算法进行算例求解,验证了考虑需求紧迫度的车辆路径规划模型的正确性和有效性。

目前众多学者在应急选址问题上已有一定基础的研究,但使用多阶段法进行研究的仍然较少。在选择综合因素评价法时,通常采用层次分析法、德尔菲法、模糊综合评价法等相对较为主观的评价方法,从而导致评价结果说服力不强;在考虑模型优化目标时,大多忽略了区域灾情程度的差异化,使得应急救援方案缺少侧重性和公平性[8]。鉴于此,采用两阶段法开展研究,第一个阶段构建备选中心优先级评价体系,采用改进的灰色关联分析和TOPSIS法相结合进行量化评价;第二阶段考虑到各受灾点不同的物资需求紧迫度,引入时间窗参数作为选址模型的影响因子,以最大限度地满足救援时间的要求,实现精准救援,为自然灾害下的物流选址问题提供新思路。

1 应急物流配送中心优先级评价体系

1.1 指标体系构建

应急物流配送中心是应急管理系统中重要的组成部分,主要负责救援物资的储备和配送,合理科学化的选址能够保证需求点及时接收物资并降低综合救援成本。许多学者在研究中常忽略了选址问题还受运输环境、道路地质、物资需求量和历史灾害风险等多种宏观因素的影响[7]。2009年,民政部发布《救灾物资储备库建设标准》,指出救灾物资储备库的规划应考虑地形、交通、地质等因素,不得选择对地质有直接危害的地区作为库址。同时根据已有的应急灾害救援经验和现有文献的研究结果,将以经济能力、物流运输能力、医疗供给能力、应急环境四个方面构建应急物流储备中心优先级的评价指标层[8],将其综合应急能力进行量化评价,对选址地点进行初步筛选,具体应急物流配送中心评价指标体系模型如图1所示。

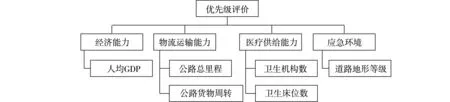
图1 物流配送中心优先级评价体系

具体指标选取原因为:

(1)经济能力:主要包括地区的人均GDP指标,备选中心的经济发展水平越高,在一定程度上其相应的物资筹备速度以及储备中心的建设速度越快。

(2)物流运输能力:主要包括公路总里程和公路货物周转量。公路总里程越大,反映地区物流建设能力越强;公路货物周转量是运输业生产总成果的指标之一,一定程度反映了地区的物流规模与运输能力。

(3)医疗供给能力:包括卫生机构数和卫生床位数,它能够反映地区的卫生医疗水平。在灾害发生后,地区医疗水平越高,应急医疗保障工作开展越快,能最大程度减少灾害死伤人数。

(4)应急环境:主要指地区道路地形等级,分为平原、盆地、高原三种地形情况,其中最理想的是平坦开阔的地形环境,可提高车辆运输物资速度。地形一般给定系数为:平原为1,盆地为0.5,高原为0.4[9]。

1.2 基于灰色关联分析-TOPSIS法的优先级评价模型构建

将灰色关联分析法与TOPSIS法相结合,从正负理想解和曲线相似性两个角度对指标进行双重评价,构造新的贴近度计算方法,确定最接近理想方案的物流备选配送中心点。具体步骤如下[10]:

(1)假设有m个受灾点样本,有n个评价指标,第i个样本的第j个指标值用Sij表示,可构建评价优先级指标矩阵Z表示为:

Z=(Sij)m×n(i=1,2,…,m;j=1,2,…,n)

(1)

(2)为消除指标间类型和维数不同的影响,使用向量度换法标准化处理,可得到一个标准化矩阵H表示为:

H=(xij)m×n(i=1,2,…,m;j=1,2,…,n)

(2)

式(2)中,

(3)

(3)熵权法确定各个指标的权重W=(w1,w2,w3,…,wn)。

(4)

(5)

(6)

(5)计算欧式距离。

(7)

(6)计算灰色关联系数,式(8)-式(9)中p为分辨率,在这里值取0.5。

(8)

(9)

(7)计算灰色关联度。

(10)

(11)

(8)对欧式距离和灰色关联度进行无纲量标准化处理。

(12)

(13)

(14)

(15)

(9)根据欧氏距离和灰色关联度的定义,对单一评价模型进行加权合并,式(16)-(17)中λ1+λ2=1,λ表示决策者偏好程度。

(16)

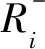
(17)

(10)计算综合评价相对贴近度Mi。这里Mi的值越大,说明物流配送中心点的综合物流能力越高。

(18)

2 模型建立

2.1 问题描述

常规物流问题的经济属性较重,通常以总系统成本最小为优化目标。通常算法模型的时间窗设置为最早开始时间和最晚满意时间,若是车辆超出规定的时间窗范围,会相应地产生等待和惩罚成本。但是应急物流具有不确定性和时效性的特点,其首要目标是对灾区的快速反应,经济属性相对较弱,因此将结合应急物流的特性对模型进行合理的调整。首先,依然将总选址成本最小化作为首要优化目标,但为了进一步提高救援效率,将增加时间窗约束。其次,将取消时间窗的最早开始时间和等待时间惩罚成本,只设置最晚满意时间约束,根据受灾点物资需求量和综合灾情需求紧迫指数进行灾情分级,灾情越严重的需求点灾情需求紧迫指数越高对应的时间窗约束越短,以保障重灾区域优先救援目标的实现[11]。

2.2 基本假设

应急物流配送中心选址是一个非确定性问题,因此为简化问题需要作出以下假设:

(1)备选配送中心和需求点的位置已知,需求点之间距离采用欧式距离计算得出;

(2)备选配送中心的最大储存量和需求点的物资需求量已知;

(3)物资运输方式采用公路运输,不考虑道路损坏程度对车辆速度的影响;

(4)每个需求点只能由一个配送中心满足物资需求;

(5)配送中心点由足够的车辆数目可满足需求,所有车辆类型与速度一样。

2.3 考虑需求紧迫度选址模型构建

根据模型描述,物流选址网络中假设有M个备选物流配送中心,备选物流配送中心集合M={i/i=1,2,3,…,m},物资需求点有N个,需求点集合为N={j/j=1,2,3,…,n},配送中心选址总费用设定包括选址建设成本、物资储备成本和物流配送成本。这时的物流选址问题属于多目标优化问题,将目标函数进行整合优化后,以下为构建的考虑需求紧迫度的应急物流配送中心选址模型为:

(19)

式(19)为总目标优化函数表达式。式(19)中ci为备选物流配送中心i的固定建设成本;wij表示为备选物流配送中心i至需求点j的物资运输量;Ri表示为备选物流配送中心i的单位储备成本;h表示为运输物资的单位距离成本;dij表示为备选物流配送中心i到需求点j的距离;xi表示当xi=1时,表示备选物流配送中心i被选中,当xi=0时,则表示备选点未被选中;yij表示为当yij=1时,表示物流配送中心i将为需求点j提供服务,yij=0时,则表示不提供服务。

(20)

式(20)为需求点物资响应时间计算公式,式(20)中tij表示为救援物资到达需求点j的响应时间;v表示为车辆行驶速度。

约束条件如下:

tij≤Tj,∀i∈M,∀j∈N

(21)

式(21)表示为各需求点的响应时间不得超过其时间约束,Tj表示为需求点j可接受的最晚响应时间约束。

(22)

式(22)表示为备选配送中心至需求点的运输物资量等于后者的需求量,sj表示为需求点j的物资需求量。

(23)

式(23)表示为配送中心对应需求点的物资需求量之和不得超过其最大储备量,ki表示为备选配送中心i的最大储备量。

(24)

式(24)表示受灾点有一个备选中心提供服务。

yij≤xi

(25)

式(25)表示备选配送中心只有在被选中时,才能对受灾点进行物资配送服务。

(26)

式(26)表示为备选物流配送中心数量限制,p表示为备选物流配送中心i被选中的数量。

2.4 算法设计

2.4.1 算法描述

应急物流选址问题是属于NP-hard问题。遗传算法是一种通过模拟自然进化过程寻找最优解的启发式算法,与其他算法相比,在求解这一类问题上具有很好的稳定性和全局搜索能力,求解算法设计过程如图2所示。

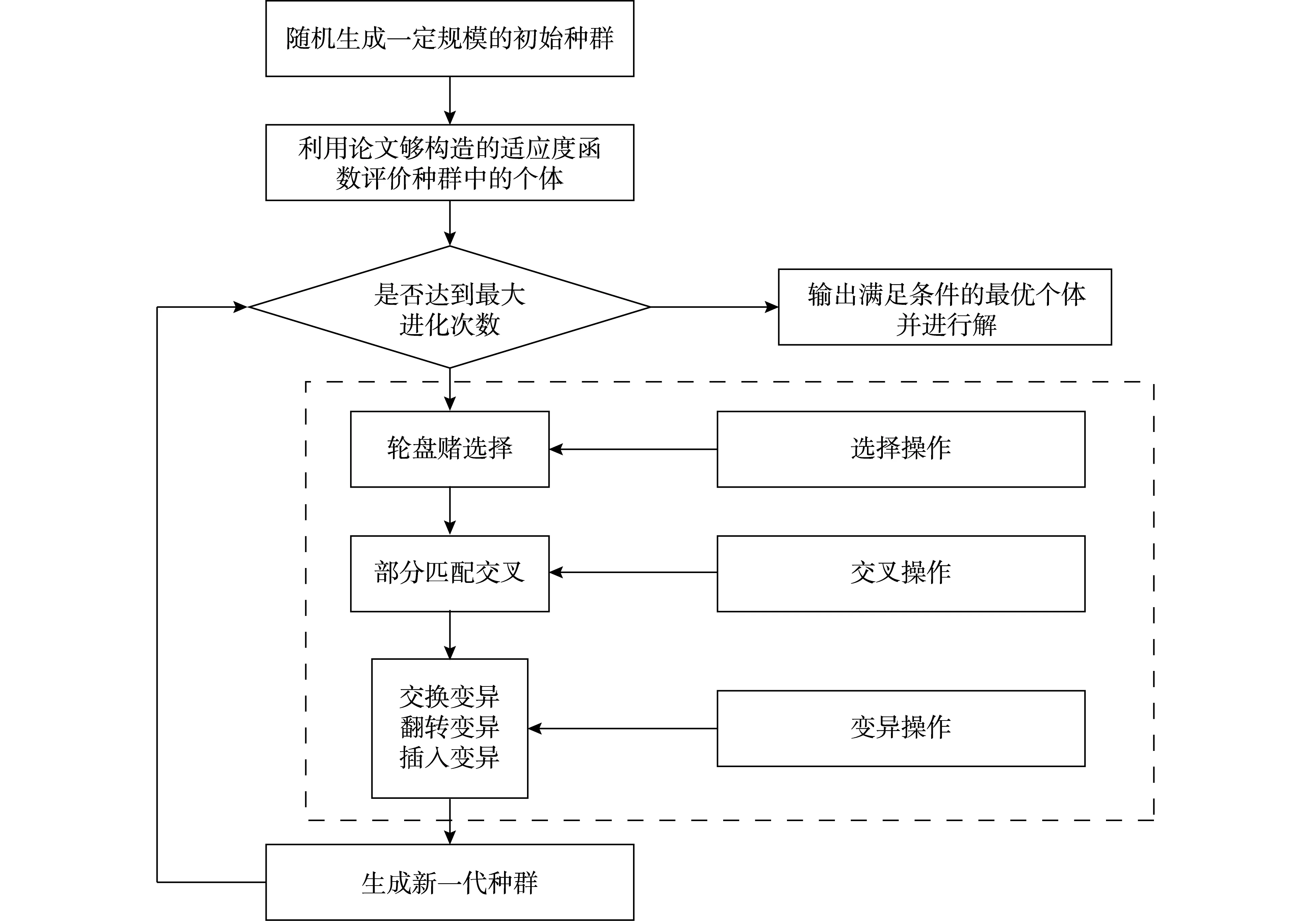
图2 遗传算法运算流程图

2.4.2 遗传算法运算流程

(1)编码和解码

遗传算法的首要过程是对染色体的编码和解码。二进制编码方式与其他编码方式相比,不仅具有广泛性,操作简单,并且更加符合生物进化规律,所以选择二进制方式进行编码。根据一定规律性,将选址的信息编码成由若干个三位二进制组成的“染色体”,编码的染色体长度和数量是由所要求的精确度决定的[11]。

(2)构造适应度函数

所构造的目标函数是为了使成本最小化,因此目标函数值最小的解就是最优解。由于是二进制编码方式,因此通常会选择线性函数作为目标函数。但是选择不当时,就会出现局部最优解,导致无法得到整体最优解的情况[12]。式(27)表示为适应度函数表达式。

(27)

(3)遗传算子的选取、交叉和变异

选择算子的目的是为了筛选出适应性较好的个体,作为亲代参与子代的繁衍,从而得到最优解。这里将使用轮盘赌法作为选择算子的方法,轮盘赌选择是根据个体适应度值与种群中所有个体适应值的比值来决定能否进入子代,从中选择出适应度大的个体。由于部分匹配交叉会进一步提高算法的收敛速度,因此遗传算子的交叉部分将选择对部分匹配交叉。变异算子是模仿染色体基因突变的现象,主要通过控制变异概率达到改变个体染色体的基因链[13]。

3 案例仿真

3.1 配送中心优先级

案例仿真对象选取地质灾害中较为典型的汶川地震。选取震中附近的10个城市作为备选应急配送中心,根据上述所建立的优先级物流配送中心评价指标体系,可对每个选址中心进行数据搜集。表1中C1为人均生产总值(元)、C2为公路总里程(km)、C3为公路货物周转量(万吨公里)、C4为卫生机构数、C5为卫生机构床位数、C6为地形系数,其信息数据来源于《2008年四川省统计年鉴》。通过计算可得到各个指标的权重为C1=0.0737、C2=0.1111、C3=0.2456、C4=0.2168、C5=0.2941、C6=0.0588,其中GDP和地形系数两个指标占比最重,其他指标占比较为接近,基本符合应急物流中对选址中心的评价要求。根据建立的优先级评价模型,可得到备选中心综合评价排序如表2所示。德阳市和眉山市综合指数较低,将这两个物流配送中心点进行筛除,得到初步的物流配送中心点。

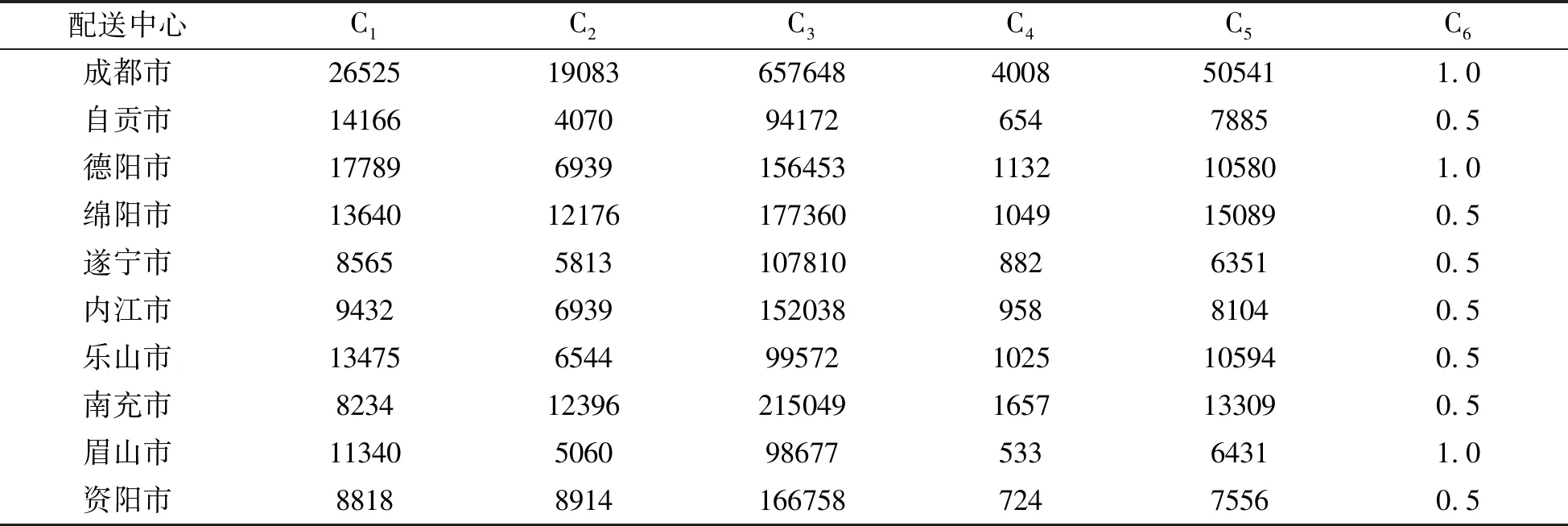
表1 物流中心点数据

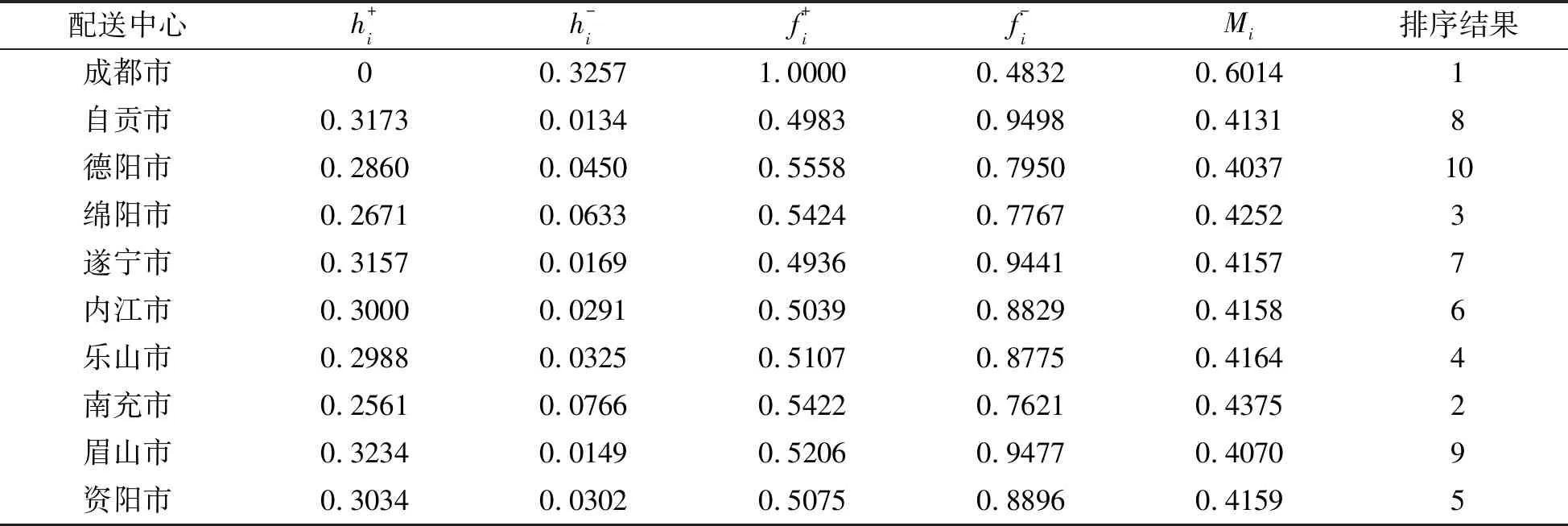
表2 备选中心优先级综合排序表

3.2 应急物流配送中心选址

在物流配送中心选址模型中,将在8个备选中心中选出6个作为最终的应急物流储备中心,各类选址成本参数设置如表3所示。选取《汶川地震灾害综合分析与评估》[14]中综合灾情指数较高的20个城市作为物资需求点,《救灾物资储备库建设标准》中储备库内仓库堆垛高度建议为3米;我国救灾物资储备规模分类表中市级的物流配送中心建设总建筑面积要求在2900～4100m2[15];因此,将案例中各市级物流备选中心分为两个等级,一类等级城市储备中心建筑面积为4100m2,二类等级城市储备中心建筑面积为3900m2,可计算出案例储备中心体积范围为11700～12300m3,其各个选址中心最大储备量和固定建设成本参数如表4所示[14]。根据杨洋[15]的研究,对于特别重大突发事件通常选取常住人口的0.04作为受灾群体,假设每个受灾人口需要一个单位的救援物资,其中包括生活物品(0.06m3)、医用物品(0.03m3)、防汛物品(0.04m3)、其他物品(0.05m3)组成,所以一个单位的物资体积合计为0.18m3;依据需求点的综合灾情等级设定时间窗参数,将灾情指数前五名的需求点设为重灾区域,其时间窗参数设置为4小时,其余的需求点时间窗设置为5小时;则各个需求点的物资需求量及时间窗参数如表5所示。从高德地图获取每个需求点的经纬度坐标,采用欧式距离法将经纬度坐标转化得到两点的距离矩阵如表6所示[16]。

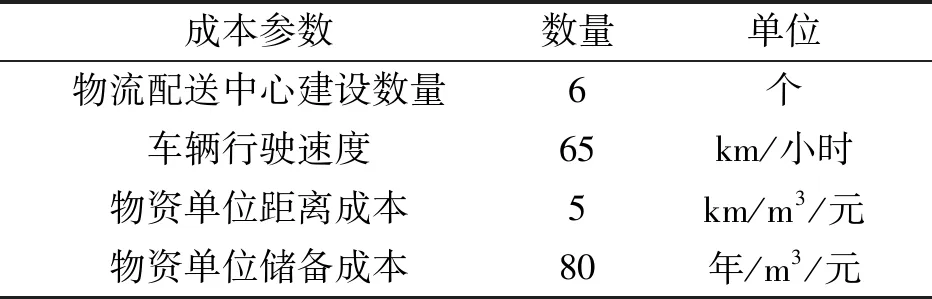
表3 各类成本参数

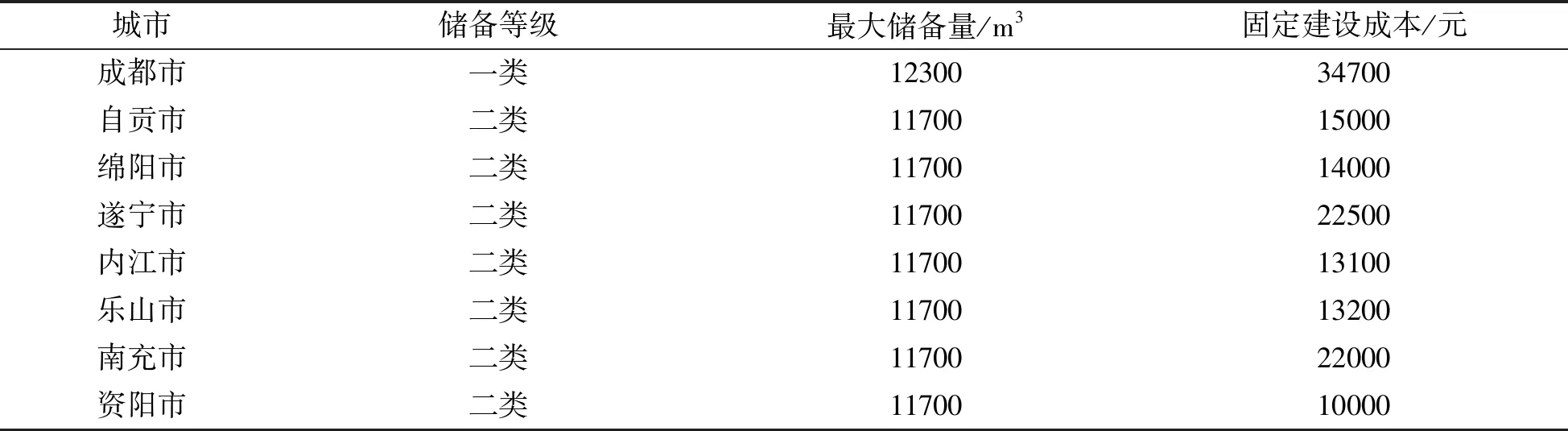
表4 各配送中心建设成本及储备量

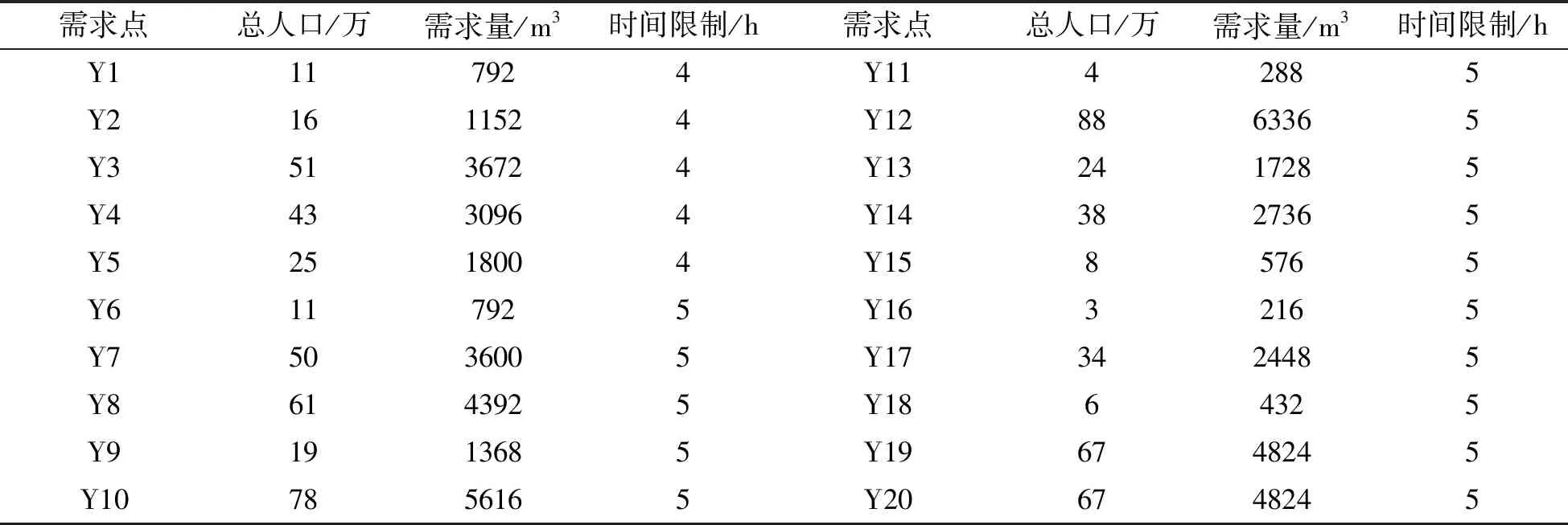
表5 各需求点需求量及时间限制

表6 各需求点到各配送中心距离矩阵 km

3.3 仿真结果分析

模型求解运行环境在1.80Ghz的Intel(R)Core(TM)i5-8250U CPU、内存为4.00GB的Windows10系统的计算机中进行[17]。遗传算法各参数设置如下:交叉概率Pc=0.8,变异概率Pm=0.05,初始化种群大小为150,最大迭代次数为200代。根据上述数据及相关参数,对模型进行求解[18]。

考虑需求点紧迫度的选址方案如表7所示,算法运行时间为7.03秒,可得到物流储备中心为成都市、自贡市、绵阳市、遂宁市、内江市、乐山市六个城市,其中南充市和资阳市将不再考虑。图3为算法迭代200次后的适应度进化曲线图,从100代后算法开始收敛,可见算法寻优能力较强。具体分配方案描述如下:成都市负责绵竹市、什邡市、理县、梓潼县、罗江县的物资,应储备超过170万个单位的物资;自贡市负责彭州市、崇州市的物资,应储备超过145万个单位的物资;绵阳市负责青川县、平武县、江油市、文县的物资,应储备超过156万个单位的物资;遂宁市负责北川县、茂县、安县、宁强县、黑水县的物资,应储备超过86万个单位的物资;内江市负责汶川县、都江堰市、小金县的物资,应储备超过80万的单位物资;乐山市负责剑阁县的物资,应储备超过67万个单位的物资[19]。

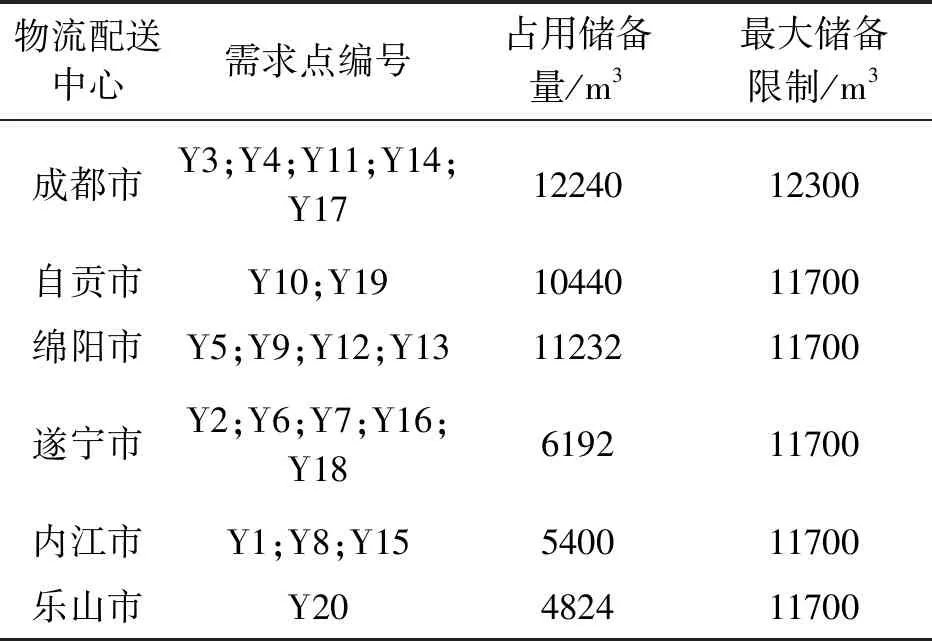
表7 考虑需求点紧迫度的应急物流选址方案

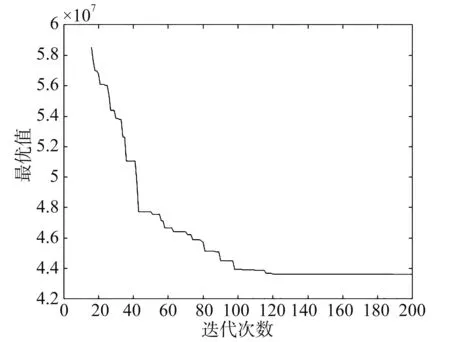
图3 算法迭代运行图

在求解不考虑需求点紧迫度的选址模型时,将忽略需求点灾情程度差异对选址中心的影响,将所有时间窗参数均设置为10小时。算法运行时长为7.88秒,具体分配结果如表8所示。具体分配方案描述如下:成都市负责什邡市、安县、理县、崇州市的物资,应储备超过164万个单位的物资;自贡市负责都江堰、彭州市、小金县的物资,应储备超过147万个单位的物资;绵阳市负责青川县、文县、梓潼县、宁强县、剑阁县的物资,应储备超过157万个单位的物资;遂宁市负责北川县、茂县、平武县、黑水县的物资供应,应储备超过52万个单位的物资;内江市负责汶川县、绵竹县的物资供应,应储备超过62万个单位的物资;乐山市负责江油市、罗江县的物资,应储备超过122万个单位的物资。

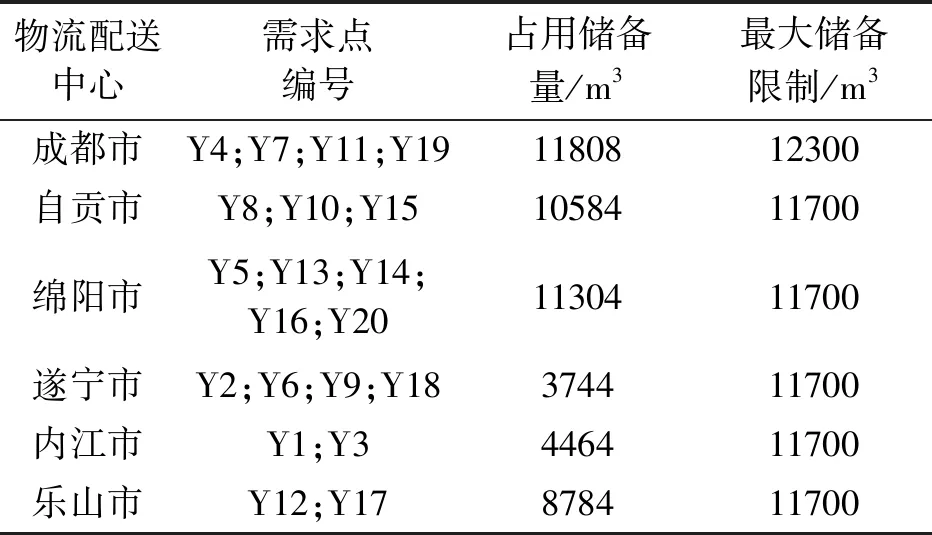
表8 不考虑需求点紧迫度的应急物流选址方案

如表9所示,整个选址配送方案中,在被选中的物流配送中心点相同的基础上,考虑时间窗的物流选址方案在需求点所花费的总物资配送时间相对优化了8.07%;尤其对需求紧迫度较高的汶川县、北川县、绵竹市、什邡市和青川县受灾点的物资等待时间相对缩短了16.65%;同时,物流配送过程中所花费的总成本相对减少了222686.80元。这表明在选址问题中增加需求紧迫度的约束,会对产生的目标函数值产生显著影响,可有效缩短总应急物资配送时间,并确保重灾区域优先得到物资保障,使得选址方案更加具有公平性和针对性,最大化程度利用有限资源,表明考虑需求紧迫度选址模型和算法更具效用性。

表9 考虑和不考虑需求急迫度选址方案对比结果

4 结论

综合研究了应急物流的特性,指出了对备选配送中心进行优先级评价的重要性,构建了以四个因素为主的评价指标体系,运用改进的灰色关联分析-TOPSIS法对备选配送中心的应急物流综合能力进行评价。分析了常规物流与应急物流的目标差异化需求,构造了单边时间窗的约束条件,并根据受灾点需求紧迫度对时间窗的设定进行合理调整。构建了由固定建设成本、储备成本和物资运输成本组成的总成本函数下带容量时间窗约束的选址模型,通过实际案例仿真与未考虑需求紧迫度的选址方案进行对比,其结果表明:时间窗约束下的选址方案不仅减少了总选址费用,而且在优化物资配送时间目标上具有明显的对比效果,能有效实现了重灾区域物资优先配送的目标。