基于频谱地图的辐射源指纹定位方法研究

杜逸潇，王红军，李修和

（国防科技大学 电子对抗学院，合肥 230037）

0 概述

随着电子通信、移动互联、计算机网络等现代科技的发展，基于无线通信的位置服务（Location Based Service，LBS）得到了越来越多的部署和应用［1］。通信基站或用户终端的地理位置信息是LBS的核心组成内容，可以为频谱资源管控、电磁态势感知、无线网络优化等提供必要的支撑［2］。高质量的LBS 依赖于精确的位置信息，而位置信息通过定位技术获取。因此，研究人员对LBS 中的定位技术进行广泛而深入的研究。

常用的定位技术分为测距定位技术和指纹定位技术。测距定位技术通过测量电磁信号的到达角度（Angle Of Arrival，AOA）、到达时间差（Time Difference Of Arrival，TDOA）、接收信 号强度（Received Signal Strength，RSS）等参数建立数学模型，进而对位置进行求解［3-5］。其中，数学模型的建立需要依靠经验公式推算和环境先验信息。在复杂环境中，经验公式往往无法正确描述环境的电磁特性且难以获取先验信息，此时建立的定位数学模型不够准确，导致定位精度降低。指纹定位技术的基本思想是利用电磁信号的某些参数在地理空间中的分布特征实现匹配定位。指纹定位过程通常包括离线阶段和在线阶段。离线阶段采集空间中信号的某些参数构建信号指纹数据库，并设计信号指纹与空间位置的定位匹配规则。在线阶段测量待定位点的信号指纹，利用指纹数据库和匹配规则实现定位［6-7］。与测距定位技术相比，指纹定位技术对存在多径效应和阴影衰落的复杂电磁环境有较好的适应性［8］，是定位技术中的研究热点之一。

在指纹定位中，通常使用接收信号强度指示（Received Signal Strength Indication，RSSI）或信道状态信息（Channel State Information，CSI）作为信号指纹，并借助机器学习算法设计指纹定位匹配规则［9］。文献［10］提出一种可变权值室内指纹定位算法，以RSSI 和欧氏距离作为权值参考计算待测节点的位置坐标，可满足室内高精度定位的需求。文献［11］将指纹定位转化为逻辑回归问题，提出一种基于深度学习框架的定位技术，在室内环境中实现亚米级定位精度的同时减少在线阶段的计算开销。文献［12］针对信号波动和多径干扰问题，采用堆叠式去噪自编码器提取噪声RSSI 中的鲁棒特征，通过信号指纹的后验概率权重和几何关系相组合的方法计算待定位点坐标，并使用约束卡尔曼滤波和隐马尔可夫模型对定位结果进行优化，进一步提高定位的精度和稳定性。为加快室外环境中的定位速度，文献［13］提出一种优化的K-means 聚类算法，用于处理信号指纹数据库，通过实验验证了所提算法的有效性。文献［14］提出一种基于半监督深度卷积生成对抗网络的指纹数据库构建算法，用于解决室外环境中建立指纹数据库所需的测量工作量较大的问题，实验结果表明，该算法显著降低了指纹数据库的构建成本。综上所述，当前对指纹定位技术的研究主要集中于指纹数据库的构建和定位匹配规则的设计。

关于指纹定位的研究已经取得了大量成果，然而多数研究人员关注的内容是在用户终端上实现接收端自定位，忽略了对信号发射端定位方法的研究。在通常情况下，接收端的定位需要采集来自多个辐射源的电磁数据，使信号指纹的特征更具多样性和复杂性，进而提高定位精度。若考虑对发射端进行指纹定位，则信号指纹仅能从单个辐射源采集，包含的信息维度较单一，在此情况下为接收端设计的指纹定位方法不再适用。针对上述问题，本文研究一种基于频谱地图的辐射源指纹定位方法。该方法使用频谱地图作为信号指纹，通过蛇优化（Snake Optimizer，SO）算法改 进的随 机森林（Random Forest，RF）空间插值算法构建指纹数据库，采用基于深度学习的神经网络算法实现匹配定位，将指纹定位技术应用到对信号发射端的定位中。

1 定位模型

本文提出的辐射源指纹定位模型包括离线阶段和在线阶段2 个部分。辐射源指纹定位模型如图1所示。

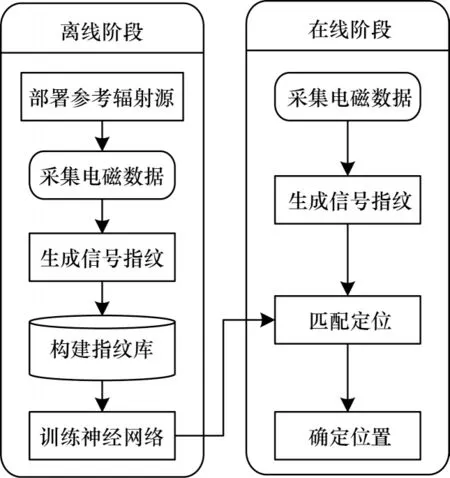
图1 辐射源指纹定位模型Fig.1 Fingerprint positioning model of radiation source

在离线阶段，首先在待测区域内部署一定数量的参考辐射源，记录参考辐射源的位置坐标；然后，在区域内投放传感器节点，组成无线传感器网络（Wireless Sensors Network，WSN），用于采集、传输和汇总参考辐射源的电磁数据。假设WSN 已对采集的原始数据完成了滤波、降噪、平滑等处理，将采集的电磁数据上传到计算中心，分别为每个参考辐射源生成对应的信号指纹。本文提出的定位模型将频谱地图作为信号指纹，用于构建指纹数据库和定位未知辐射源。

频谱地图又称无线电环境地图（Radio Environment Map，REM）、电磁环境地图等，是对电磁环境综合信息的可视化定量描述［15］，可用于接收信号强度指示、接收信号码功率（Received Signal Code Power，RSCP）等表征信息。频谱地图能够结合实际的地理环境描述电磁信号在特定区域中的覆盖情况，可以反映辐射源的数量和分布，因此其本身涵盖了一定的辐射源位置信息［16］。

在参考辐射源的信号指纹生成后，与对应的位置坐标存储在一起，共同构成指纹数据库。最后，利用该数据库中的信号指纹和位置坐标，通过监督学习方法训练一个神经网络模型，用于后续过程的匹配定位。

在线阶段基于待定位辐射源的信号指纹估计出其位置。首先，通过WSN 采集待定位辐射源的电磁数据；然后，利用采集的数据构建频谱地图，得到信号指纹；最后，使用离线阶段训练好的神经网络模型，将待定位辐射源的信号指纹作为输入，得到估计的位置坐标，完成定位。

2 算法设计

2.1 信号指纹生成算法

在本文提出的定位模型中，信号指纹的生成过程就是对区域内频谱地图的重构。空间插值法是构建频谱地图的常用方法。由于空间插值法仅需要传感器测量的数据，而不依赖任何先验信息，因此可用于生成信号指纹。经典的空间插值法包括克里金（Kriging）插值法、反距离加权（Inverse Distance Weighted，IDW）法、自然邻点插值（Natural Neighbor Interpolation，NNI）法等确 定性算 法，其中，Kriging 插值法具有最高的构建精度［17-18］。除此之外，部分机器学习算法也可以实现空间插值，相较于经典插值算法有更优的性能表现［19］。本文使用蛇优化算法改进的随机森林空间插值算法构建频谱地图。

2.1.1 随机森林空间插值算法

随机森林算法是一种集成学习算法，对非线性和高维数据有较好的处理能力，可用于分类或回归任务。空间插值可以被视为一种多变量回归问题，因此能够通过RF 回归算法实现。基于RF 的空间插值算法已在气候学、地质学等领域的空间数据建模中获得广泛应用［20-22］。

RF 的基础是决策树（Decision Tree，DT）算法。DT 算法通过一系列优选分割规则，将原始的输入特征空间划分为有限个子空间，当预测时由输入数据在各个子空间上的取值共同决定输出结果。RF 采用bagging 方法集成了大量DT 模型，与DT 算法相比减少了过拟合现象的发生，具有更优的稳定性。在训练过程中，RF 通过bootstrap 重采样方法从数据集中抽取子集，并使用随机选择的特征为每个子集训练DT 模型。对于回归问题，RF 的输出结果取各DT模型输出结果的平均值得到。随机森林回归算法示意图如图2 所示。

图2 随机森林回归算法示意图Fig.2 Schematic diagram of random forest regression algorithm

当训练数据为测量点的属性特征，回归目标为待插值点的属性特征时，RF 回归可用于空间插值中。文献［23］提出一种随机森林空间插值（Random Forest Spatial Interpolation，RFSI）算法，该算法基于RF 回归，使用待插值点附近测量点的观测值和它们之间的距离作为特征，估计待插值点处的观测值。RFSI 可表示为：

其中：s0为待插值点；sn(n=1,2,…,Np)为待插值点附近最近的Np个测量点；z(sn)和d(sn)分别为对应的测量值和距离；为待插值点的估计值；F为RF 回归模型。文献［23］的实验结果表明，RFSI 优于多数经典的确定性空间插值算法。

2.1.2 蛇优化算法

蛇优化算法是一种高效的元启发式算法，通过模仿蛇的交配行为寻找搜索空间中的最优解［24］。蛇的交配行为受食物和温度因素的共同影响。如果食物充足且温度较低，蛇群发生交配行为，否则蛇只会寻找食物。SO 算法分为勘探阶段和开发阶段，分别模拟在食物充足和食物不足2 种条件下蛇种群的行为模式。

SO 算法首先进行初始化，生成均匀分布的随机蛇种群，如式（2）所示：

其中：Gi为第i个蛇的位置；Gmax和Gmin分别为搜索空间的上边界和下边界；r为介于0 和1 之间的随机数。SO 算法将种群分为雄性组和雌性组，设雄性组的数量为Nm，雌性组的数量为Nf，则：

其中：Ntotal为种群的总数量。在生成蛇种群后，根据适应度函数计算每个个体的适应度值。

食物数量和温度的定义如式（5）和式（6）所示：

其中：d为当前迭代次数；D为最大迭代次数；c1为一常数，令c1=0.5。

若Q<0.25，即食物不足时，蛇种群处于勘探阶段，个体搜索食物并更新位置：

若Q>0.25，即食物充足时，蛇种群处于开发阶段。此时，如果Temperature>0.6，蛇种群只会寻找食物，位置更新方式为：

其中：Gi,j为雄性或雌性个体的位置；Gfood为当前适应度值最优的最佳个体位置；c3为一常数，令c3=2。如果Temperature<0.6，蛇种群将处于战斗或交配模式。

在战斗模式下，个体位置更新的方式为：

其中：Mm和Mf分别表示雄性和雌性的交配能力。Mm和Mf定义为：

SO 算法在达到最大迭代次数或设定的适应度阈值后，返回位置最优的个体，得到搜索空间中的最优解。

2.1.3 改进的随机森林空间插值算法

在RFSI 算法中，邻近测量点数量Np的选取直接影响插值估计的精确度。在文献［23］中Np的取值需要依靠人为设定，不同的场景下不能确保Np总是取到最优。同时，DT 模型的数量Nt也是一个重要的参数，对RFSI 的拟合和泛化能力有着重要的影响。本文提出一种蛇优化算法改进的随机森林空间插值算法（SO-RFSI），利用SO 算法对RFSI 算法中的参数Np和Nt进行优化。SO-RFSI算法的流程如图3 所示。

图3 SO-RFSI 算法流程Fig.3 Procedure of SO-RFSI algorithm

SO-RFSI 算法具体步骤如下：1）通过随机抽取的方式将测量点的数据划分为训练数据和验证数据；2）初始化SO 算法的种群；3）使用训练数据和初始化蛇种群训练RF 回归模型；4）根据适应度函数计算蛇种群中个体的适应度值；5）找出蛇种群中位置最优的个体；6）判断是否满足迭代停止条件，若最优个体的适应度值满足设定的阈值或迭代达到最大轮次，则停止迭代，转入步骤8），否则转入步骤7）；7）SO 算法更新种群位置，并使用新种群训练RF 回归模型，转入步骤4）；8）保存最优个体赋值的RF 回归模型，该模型为具有最佳参数的最优化模型；9）利用最优RF 回归模型计算待插值点的估计值。

在SO-RFSI 算法中，由L只蛇组成的种群表示为：

其中：Np1,Np2,…,NpL和Nt1,Nt2,…,NtL分别为参数Np和Nt在搜索空间内的具体取值。适应度函数定义为：

其中：z表示测量点的实际值；表示训练或验证过程中测量点的预测值；si和sj分别为训练数据点和验证数据点；Strain和Sval分别为训练数据和验证数据的数量为训练 数据的 均方根误差，反 映RF 回归模 型的拟 合能力；为验证 数据的均方根误差，反映RF 回归模型的泛化能力。

SO-RFSI 算法的伪代码表示如算法1 所示。

算法1SO-RFSI 算法

假设RFSI 算法中训练RF 回归模型的复杂度为O(f(m1))，使用模型插值估计的复杂度为O(g(m2))，则RFSI的复杂度为O(f(m1)+g(m2))。对于SO-RFSI，若种群的个体数为L，最大迭代次数为D，算法步骤中划分数据集和SO 初始化的执行时间为δ1，计算适应度值和寻找最优个体的执行时间为δ2，SO 更新种群位置的执行时间为δ3，则算法的复杂度为O(δ1+DL(f(m1)+δ2)+(D-1)δ3+g(m2))。由于D和L为已知常数，且δ1、δ2和δ3通常较小，因此SO-RFSI 算法的复杂度表示为O(f(m1)+g(m2))。由此可见，SO-RFSI 算法的复杂度相对于RFSI 算法并未增加。

2.2 指纹匹配定位算法

指纹匹配定位算法基于深度学习框架实现。深度学习建立于人工神经网络和反向传播算法基础上，擅长获取样本数据内在的复杂变化规律。在线阶段利用深度学习框架进行定位，无需查询指纹数据库，能够缩短计算时间，有利于提高定位效率。

卷积神经网络（Convolutional Neural Network，CNN）是一种重要的深度学习模型，已经在图像处理和计算机视觉领域取得了巨大成功［25］。CNN 可以直接将二维图像数据作为输入，避免了复杂繁琐的人工特征工程。频谱地图作为一种特殊的二维图像数据，能够通过CNN 进行处理。本文使用频谱地图和辐射源位置坐标作为样本和标签训练神经网络，基于CNN 模型完成匹配定位，具体网络结构如图4 所示。该网络分为输入层、卷积层、平均池化层、全连接层和输出层。输入层对频谱地图做归一化等预处理操作，避免因初始化权值过大导致梯度爆炸，同时加快网络收敛。经过预处理后，将频谱地图输入到卷积层。卷积层共有4 层，使用的卷积核由浅层到深层的数量分别为64、64、128、256，尺寸大小均为3×3，卷积计算的步长均为1。在每个卷积层后连接一个平均池化层，以步长为2、大小为2×2 的窗口对卷积层的输出数据进行降采样处理。卷积层与平均池化层的组合能够在提取频谱地图特征信息的同时减少网络中的超参数量。平均池化层的尾部连接3 个全连接层，神经元个数分别为64、8、2。全连接层对提取的特征信息做非线性映射，将其关联到目标输出。最后，输出层对全连接层的映射结果进行反归一化处理，得到辐射源的二维空间坐标。网络中卷积层的激活函数为ReLU，全连接层的激活函数为Sigmoid 函数，采用Dropout策略防止过拟合现象的发生。

图4 基于CNN 的匹配定位网络结构Fig.4 Structure of matching positioning network based on CNN

3 仿真实验

为验证本文所提定位模型与算法的有效性，本文使用MATLAB R2020b 软件进行仿真实验与分析。

3.1 实验环境与评估指标

本文以4G-LTE 移动通信基站为实验对象，选取面积为4 km×4 km 的某室外地区作为目标区域进行仿真实验。通过射线追踪法［26］对无线电波的传播进行建模，模拟基站在不同位置时目标区域的电磁环境，利用WSN 采集测量点的电磁数据，用于生成信号指纹。实验环境示意图如图5 所示。离线阶段和在线阶段均以随机投放的方式部署传感器节点。本文实验共收集了392 组数据，其中50%划分为训练集，50%划分为测试集。

图5 实验环境示意图Fig.5 Schematic diagram of experimental environment

理想的频谱地图是连续的曲面，但是在实际应用时通常用离散数据点组成的二维数组表示。仿真实验在x轴和y轴以20 m 为间隔，对目标区域进行网格化处理。本文使用网格点处的RSSI 值表征频谱地图。令Nmeas为测量点总数，Ngrid为网格点总数，则测量点占比为：

采用均方根误差（Root Mean Square Error，RMSE）衡量频谱地图的构建质量，RMSE 计算式为：

其中：RSSI(si) 为网格点si处的实际RSSI 值；为si处插值得出的RSSI 估计值。

本文采用平均定位误差和累积分布函数（Cumulative Distribution Function，CDF）评估定位性能。假设(xj,yj)为某基站的实际位置，为该基站的估计位置，定位误差为两者之间的欧氏距离，如式（26）所示：

CDF 通过计算变量小于或等于某值的概率来描述变量的概率分布，定义如式（28）所示：

CDF 越早趋于平滑，说明定位性能更稳定。

3.2 实验结果与分析

图6 所示为Kriging 算法、RFSI 算法和SO-RFSI算法在不同测量点占比条件下的频谱地图构建质量。RFSI 算法的参数Np设为5，Nt设为75。从图6可以看出：随着测量点比例的增加，3 种插值算法的RMSE 均下降。其中，SO-RFSI 算法的RMSE 始终最低，表明该算法构建的频谱地图准确度最高。由于人为设定的参数无法取到最优，因此RFSI 算法在测量点占比较低时的性能表现最差。在测量点占比较高的情况下，用于训练RF 回归模型的数据增加，RFSI 算法能够充分发挥机器学习技术的优势，此时的性能优于Kriging 算法，与SO-RFSI 算法相近。图6 的实验结果验证了RFSI 算法中参数选取的重要性，同时表明本文提出的SO-RFSI 算法是对RFSI 算法的有效改进。

图6 不同空间插值算法的性能对比Fig.6 Performance comparison among different spatial interpolation algorithms

本文通过消融实验进一步分析SO-RFSI 算法的性能，设置2 组对照算法，分别命名为SO-RFSI-1 和SO-RFSI-2。SO-RFSI-1 算法利用SO 算法优化RFSI算法的参数Nt；SO-RFSI-2 算法利用SO 算法优化RFSI 算法的参数Np。RFSI、SO-RFSI-1、SO-RFSI-2和SO-RFSI 构建的频谱地图质量对比如图7 所示。从图7 可以看出：RFSI算法的RMSE 最高，SO-RFSI-1算法的RMSE 低于RFSI 算法但高于SO-RFSI-2 算法，SO-RFSI 算法的RMSE 最低。上述实验结果表明，通过合理设置RFSI 算法中的参数Nt或Np均可以提高频谱地图的构建质量，且Np的改善效果更为明显。

图7 RFSI、SO-RFSI-1、SO-RFSI-2 和SO-RFSI 构建的频谱地图质量对比Fig.7 Comparison of spectrum map quality constructed by RFSI，SO-RFSI-1，SO-RFSI-2 and SO-RFSI

图8 所示为使用不同的空间插值算法作为信号指纹生成算法的平均定位误差。本文分别采用Kriging 算法和SO-RFSI 算法生成信号指纹，然后基于CNN 模型完成离线阶段训练和在线阶段定位，并计算平均定位误差。随着测量点占比的增加，2 种定位算法的平均定位误差均下降，SO-RFSI-CNN 始终优于Kriging-CNN。从图8 与图6 的实验结果对比可以得出：采用空间插值构建的频谱地图准确度越高，则越有利于减小定位误差。因此，通过SO-RFSI 算法生成信号指纹具有合理性。

图8 信号指纹生成算法对平均定位误差的影响Fig.8 Influence of signal fingerprint generation algorithms on average positioning error

图9 所示为当测量点占比为0.1 时，本文算法与文献［13-14］中定位算法的误差CDF。表1 所示为在该条件下3 种算法的平均定位误差。从图9 可以看出：本文算法在误差为20 m 时的置信概率约为84.5%，而文献［13］算法和文献［14］算法的置信概率分别约为2.69%和23.35%。本文算法的累积定位误差明显小于其他2 种算法，定位性能更稳定。从表1可以看出：本文算法的平均定位误差最低且定位精度最高。综合图9 和表1 的实验结果可以得出，本文算法在定位精度和稳定性方面均有优势，取得了最优的定位效果。

表1 3 种定位算法的平均定位误差 Table 1 Average positioning errors of three positioning algorithms 单位：m

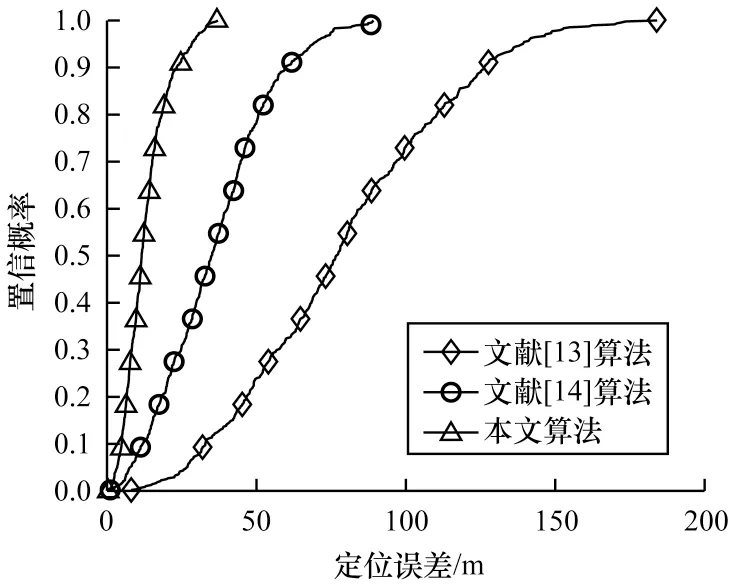
图9 不同算法的定位误差累积分布函数对比Fig.9 Positioning error cumulative distribution function comparison among different algorithms

4 结束语

本文提出一种针对信号发射端的辐射源指纹定位方法。该方法使用频谱地图作为信号指纹，基于深度学习神经网络算法实现指纹匹配定位。通过SO-RFSI 算法构建待测区域的频谱地图，同时生成信号指纹，建立指纹数据库并训练卷积神经网络模型，将待定位辐射源的信号指纹输入到卷积神经网络模型中，得到估计的位置坐标。本文研究指纹定位方法的实质是利用卷积神经网络学习频谱地图中蕴含的辐射源位置信息，频谱地图的构建质量越高，则越有利于提高定位性能。实验结果表明，本文所提的定位模型与算法具有较优的定位精度和定位稳定性，可用于对信号发射端进行指纹定位。后续将经典空间插值算法与机器学习技术相结合，改善在低测量点占比时的频谱地图构建质量，进一步提高指纹定位的性能。