基于改进ORB特征提取的快速三维重建算法

罗庆 唐清善

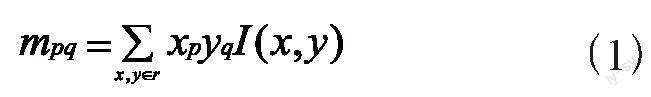
摘  要：鉴于多视图三维重建算法的特征检测和匹配能力较差，文章提出一种基于改进ORB特征提取的快速三维重建算法。该算法针对传统算法在建筑数据采集中的重建效果差和运行效率低的问题进行了优化，首先运用改进的ORB算法进行特征点提取，采用GMS算法进行特征匹配，得到匹配结果后利用全局式SFM对场景相机位姿进行估计，之后再进行光束法平差，最后利用PMVS算法得到稠密重建的结果。实验结果表明，该算法在三维重建运行效率上有所提升，能够满足快速的三维重建要求。

关键词：全局式SFM；ORB算法；GMS算法；光束法平差

中图分类号：TP391.4；TP312 文献标识码：A 文章编号：2096-4706（2023）15-0083-05

A Fast 3D Reconstruction Algorithm Based on Improved ORB Feature Extraction

LUO Qing， TANG Qingshan

（School of Physics & Electronic Science， Changsha University of Science & Technology， Changsha  410114， China）

Abstract： In view of the poor feature detection and matching ability of multi view iterative reconstruction algorithm， this paper proposes a fast iterative reconstruction algorithm based on improved ORB feature extraction. This algorithm has been optimized to address the issues of poor reconstruction performance and low operational efficiency of traditional algorithms in building data collection. Firstly， the improved ORB algorithm is used for feature point extraction， and the GMS algorithm is used for feature matching. After obtaining the matching results， the global SFM is used to estimate the camera pose of the scene， followed by bundle adjustment. Finally， the PMVS algorithm is used to obtain the dense reconstruction results. The experimental results show that the algorithm improves the running efficiency of iterative reconstruction and can meet the requirements of fast iterative reconstruction.

Keywords： global SFM; ORB algorithm; GMS algorithm; bundle adjustment

0  引  言

多視图三维重建技术是指通过三维物体的二维投影来恢复三维形状的技术[1]，目前基于运动恢复结构（Structure From Motion， SFM）的算法是多视图三维重建研究的热点方向[2]。

图像特征提取和匹配是三维重建流程研究中较为重要的内容，目前多视图三维重建大多是基于特征提取算法SIFT（尺度不变特征变换）[3]来实现。该算法能够在不同尺度和旋转的情况下得到较好的匹配结果，但由于使用了128维描述符，计算过于复杂导致匹配效率低下。针对这一问题，以下研究者给出了不同的解决办法。文献[4]提出基于Bicular算法的自适应尺度结合Harris算法改进SIFT算法，具有更强的特征点检测与匹配能力；文献[5，6]提出基于AKAZA算法的多视图三维重建改进方法，以AKAZA算法为基础一定程度上提高了重建的效率，但使用单应性矩阵迭代随机采样一致算法模型耗时较长。传统ORB特征提取算法提取特征点数较多且提取速率快，但所提取的特征点分布不均匀且存在误匹配较多的情况，为此，通过四叉树原理[7]对图像进行分区域特征提取得到均匀分布的特征点后，使用GMS（Grid-based Motion Statistics）[8]算法对特征点进行匹配。结合GMS特征匹配和ORB特征点提取算法的效果较传统ORB算法和其他同类特征匹配算法更好[9]。Tamilarasi[10]提出的增量式SFM重建算法，通过挑选基准图像再叠加新的图像并进行光束法平差优化后得到点云，文献[11-13]在增量式方法的基础上提高了重建效率，但该方法只有在序列图像较少的情况下才能获得较好的重建效果和运行效率，当图像增多时耗时和误差也会骤然变大。

针对上述问题，提出基于四叉树和改进ORB特征提取的快速三维重建算法，运用ORB算法进行特征提取和暴力匹配后引入GMS算法对粗匹配点进行筛选，采用全局式SFM[14]算法得到稀疏点云后再使用PMVS算法得到稠密点云，从而完成多视图几何三维重建。

1  基于ORB特征提取的全局式SFM算法

1.1  特征检测与匹配

1.1.1  ORB特征提取

1.1.1.1  特征点提取与筛选

首先对图像特征点进行粗提取，通过机器学习的方法筛选粗提取的匹配点，运用基于四叉树的划分[15]算法来筛选最优的FAST角点。设置自适应阈值，在提取的特征点达到期望值后结束提取以减少算法运行时间，从而避免了传统ORB算法的冗余扎堆现象，得到均匀的特征点，有利于匹配精度的提升。

1.1.1.2  计算特征点的灰度质心

ORB算法借助矩法来确定FAST特征点的方向，通过矩来计算以特征点为中心r半径范围内的质心，特征点和质心之间的向量作为该特征点的方向。矩的定义为：

其中，I （x， y）表示图像灰度，该矩质心为：

根据质心坐标得到特征点方向：

1.1.1.3  BRIEF算法描述

经过上一步我们可以确定图像的关键点，现在需要通过BRIEF算法将这些关键点转化为特征向量。该算法的主要思想是比对特征点与周围邻域多个点对之间的灰度大小，得到0或1两种结果，算式为：

其中，I （x）与I （ y）分别表示该点的像素值，得到结果形成二进制编码串，该编码串的长度通常为128～512，代表着该描述子的属性和周围邻域信息，这一特性使得BRIEF的运算速度非常快。通过下式将每点得到的τ （ p; x， y）构成此目标点的BRIEF特征描述子：

1.1.2  GMS算法图像匹配

假设IA和IB为输入图像，IA到IB图像的最近邻匹配集合为T ={t1，t2，…，ti，…，tN}，ti表示其中的一个图像匹配对，假定正确的匹配点邻域内还有Si个匹配点支持它，其中Si = | λ | - 1，由于每个特征点之间相互独立，其邻域内支持量Si服从二项式分布，如式（7）所示：

其中，Pt和Pf分别表示正确匹配和错误匹配时邻域窗口支持的概率，R表示邻域内匹配对的数量。Si的数学期望及标准差为：

根据期望Ef和标准差Sf可以确定正确匹配和错误匹配的可区分度：

ε=Ef+aSf（10）

Ef的大小可以忽略不计，统计网格中对所有特征匹配对的邻域支持量为Si，保留Si＞ε作为正确的匹配点对。

1.2  SFM算法

1.2.1  求解基础矩阵

设第一帧下P点空间位置为[X， Y， Z]，根据针孔相机模型得到像素点位置分别为KP、K （RP + t），其对极几何关系为：

PT2K（-T）T^PK-1P1=0（11）

其中，P1和P2表示不同图像的对应特征点对，该式简洁描述了匹配点之间的空间位置关系。

1.2.2  相机旋转和平移向量求解

三维旋转变换可以用3×3的正交矩阵T表示，相机i和j之间的旋转关系可以表示为：

Tij=TjT-1i（12）

相机平移求解以相机旋转结果作为输入，相机相对于全局坐标系的平移向量可通过式（13）求得：

Eij=TTi（[ti]x-[tj]x）Tj（13）

2  仿真实验与分析

2.1  全局式SFM三维重建流程和实验环境

改进的基于ORB特征提取的全局式SFM三维重建算法主要流程如下：

1）輸入图像序列，提取图像信息，生成EXIF文件。

2）使用改进的ORB算法提取特征点和暴力匹配算法后得到特征粗匹配对，使用GMS算法进行特征匹配筛选得到均匀的匹配点对。

3）根据匹配的特征点计算序列图片之间的空间位置关系，并计算出相机的全局旋转矩阵和全局平移矩阵。

4）利用光束法平差优化重投影误差，得到稀疏点云。

5）使用基于面片的多视图立体算法得到稠密点云。首先利用稀疏点云特征点与其相邻点结合图像信息得到面片并进行扩展，过滤掉错误面片后得到稠密点云。

本系统是在Ubuntu 16.04平台上开发的，仿真依赖库为OpenMVG、OpenMVS和OpenCV，硬件环境为Intel Core i5-8250U（1.6 GHz），开发语言为C++。

2.2  图像配准实验

在多视图三维重建中，图像特征点的提取和匹配作为最基础的部分，其匹配效率和匹配精度也影响着整个三维重建流程的效果。本次实验将使用序列建筑图像作为输入，检验图像特征匹配的数量、精度和时间复杂度。其中相机焦距为35 mm，图像分辨率为2 592×3 872。实验中使用的部分序列图像和不同算法匹配结果如图1和图2所示。

在图像配准实验中分别利用SIFT、ORB和本文算法进行图像特征提取和匹配，对如表1所示的匹配结果进行分析可知，本文算法在粗匹配点数和精匹配点数上都取得了很好的结果。其中精匹配是由粗匹配经过随机抽样一致算法得到的，精匹配点数达到2 727，匹配准确率也高于SIFT算法和传统ORB算法，达到了98.7%，匹配效率即单位时间精匹配点，本文算法为1 934点/秒，SIFT和传统ORB算法分别为295点/秒和1 293点/秒。在特征检测与匹配耗时上本文算法分别为SIFT和传统ORB算法的15.25%和66.85%，而在特征点匹配能力上较之两种算法均有所提高。

将本文特征匹配算法应用到多视图三维重建的流程中，其中使用数据集序列图像数量为543张，以下实验将三组不同图像特征匹配算法在三维重建中的时间复杂度进行对比。如表2所示。

表2描述了不同特征提取算法在三维重建流程中的时间复杂度，在特征提取和匹配过程中，SIFT平均每张图片耗时7.9秒，传统ORB单张耗时2.47秒，改进ORB算法单张耗时为1.96秒，改进ORB算法耗时为SIFT的24.8%，是传统ORB算法的79.35%。从该组实验可以看出，基于改进ORB算法的特征提取和匹配的耗时更少，提高了三维重建流程的运行效率，进一步实现了快速的三维重建。ORB特征提取算法的主要特点是提取速度快，但特征点的鲁棒性较差，容易产生错误的匹配点。基于GMS算法的运动统计特性（即一个正确的匹配点周围也一定存在足够多的匹配点来支撑匹配），结合改进ORB和GMS两种算法可以得到一种速度快且质量好的特征匹配方法。得到特征匹配的结果后，继续往下进行完成实验。

2.3  SFM三维重建试验

图3和表3分别给出不同算法的三维重建可视化结果和重建数据，从可视化的角度来看，在稠密点云上全局式ORB算法得到的结果拥有更加清晰的边缘，孔洞也更少，可视化效果最佳。

仅从增量式三维重建数据上分析，基于改进ORB算法的三维重建所能得到的稀疏点云比基于SIFT算法增加了24.27%，比基于传统ORB算法增加了39.62%，稠密点云数分别增加17.49和27.27%。采用全局式ORB算法得到的稀疏点云相较于前三种算法分别增加35.23%、51.94%、8.82%，而稠密点云分别增加28.28%、38.96%、9.18%，重建效率相较于增量式ORB算法提升28.56%，可以看到全局式ORB算法得到的稠密点云具有更加丰富的纹理信息。综上，基于本文算法的三维重建系统在该数据集中表现出更加优异的性能，不仅得到了更加丰富的点云信息，在三维重建效率上也比增量式重建有所提升。

通过二维图像生成三维模型后，由于受噪声等因素的干扰，所生成的三维模型再反投影至二维图像，初始位置与该投影点并不会完全重合，假设将所有投影点与该点原始位置之间距离平方和均值的平方根作为重建的均方根误差，可表示为：

基于ORB算法的全局式三维重建最终得到的均方根误差为0.28，在增量式重建中本文算法得到的重建误差低于其他重建算法，表示基于改进ORB算法的三维重建模型在一定程度上减小了重投影误差，这是因为该算法得到的匹配点对更加准确，误匹配率更低，在通过特征点生成三维空间点时因误匹配带来的干扰也更小，而增量式和全局式三维重建算法所产生的重建误差的差异主要是因为增量式三维重建会随着图像的加入不断进行光束法平差而产生误差的累积，而全局式三维重建考虑了相邻相机之间的空间关系，不会导致重建结果的漂移，并且这种差距会随着序列图像数量的增加而变大。

3  结  论

针对传统增量式三维重建算法存在重建效率和重建精度低的问题，提出一种基于改进ORB算法的三维重建，实验结论如下：

1）基于改进ORB算法得到的特征点更精确，在匹配能力上要高于其他同类算法，并且提高了匹配效率。

2）将改进的ORB算法运用到三维重建系统中能够获得更加稠密的点云，降低了重建误差，验证了改进ORB算法应用于三维重建系统的可行性。

3）使用全局式三维重建算法能够改进增量式重建产生的误差累积问题，有效减小了均方根误差，提升了重建效率，在可视化角度上得到的稠密点云边缘更加清晰，孔洞更少。

参考文献：

[1] 郑太雄，黄帅，李永福，等.基于视觉的三维重建关键技术研究综述 [J].自动化学报，2020，46（4）：631-652.

[2] 王巧丽，徐增波，张玲.基于运动恢复结构三维重建的应用与研究进展 [J].毛纺科技，2021，49（7）：95-98.

[3] LOWE D G. Distinctive Image Features from Scale-Invariant Keypoints [J].International Journal of Computer Vision，2004，60（2）：91-110.

[4] 普阳光.改进ASIFT算法的PMVS三维重建 [J].计算机时代，2018，312（6）：69-71.

[5] 周泩朴，耿国华，李康，等.一种基于传统AKAZE算法的多视图几何三维重建方法 [J].计算机科学，2018，45（S2）：180-184+207.

[6] 郝豪杰，李朝奎，方军，等.改进的传统AKAZE特征提取的全局式SFM三维重建算法 [J].测绘科学技术学报，2021，38（5）：492-498.

[7] 倪翠，王朋，孙浩，等.一种基于四叉树划分的改进ORB算法 [J].应用科学学报，2022，40（2）：266-278.

[8] BIAN JW，LIN WY，MATSUSHITA Y，et al. GMS： Grid-based motion statistics for fast， ultra-robust feature correspondence [C]//2017 IEEE Conference on Computer Vision and Pattern Recognition （CVPR）. Honolulu：IEEE，2017：2828-2837.

[9] 潘峰，沈建新，秦顺，等.融合GMS的ORB特征点提取与匹配算法 [J].计算机工程与设计，2022，43（8）：2244-2251.

[10] TAMILARASI M，DURAISWAMY K. Genetic based Fuzzy Seeded Region Growing Segmentation for Diabetic Retinopathy Images [EB/OL].[2023-02-02].https：//www.zhangqiaokeyan.com/academic-conference-foreign_meeting-294498_thesis/0705018999867.html.

[11] SNAVELY N，SEITZ S M，SZELISKI R. Modeling the world from Internet photo collecting [J].International Journal of Computer Vision，2008，80（2）：189-210.

[12] WU C C. VisualSFM： A visual structure from motion system [EB/OL].[2023-02-04].http：//ccwu.me/vsfm/index.html.

[13] RAMMALINGAM S，ANTUNES M，SNOW D，et al. Line-sweep： Cross-ratio for wide-baseline matching and 3D reconstruction [C]//2015 IEEE Conference on Computer Vision and Pattern Recognition （CVPR）. Boston：IEEE，2015：1238-1246.

[14] MICHELETTI N，CHANDER J H，LANE S. Structure from motion （SFM） photogrammetry [EB/OL].[2023-01-25].https：//www.researchgate.net/publication/293108194_Structure_from_motion_SFM_photogrammetry.

[15] 彭智東，宣士斌.融合最小生成树和四叉树的图割图像分割方法 [J].计算机技术与发展，2018，28（12）：102-105+126.