轴向柱塞泵的空穴流动特性分析与优化
2023-09-17贠振刚刘沛汉李资
贠振刚,刘沛汉,李资
(新疆工程学院 能源工程学院,乌鲁木齐 830091)
轴向柱塞泵作为液压系统的核心元件,以其可控性、结构紧凑、灵活性等优点,广泛应用于工程机械、船舶、航空、军事、机器人等领域中[1]。但由于在高压高转速工况下,容易产生振动和高噪声,导致泵中配流盘、滑靴等零部件磨损,进而导致机械发生故障,给国家和人民生命财产安全带来了严重威胁[2]。首要任务是优化柱塞泵结构、提高自吸能力、减少磨损等因素[3]。为降低柱塞泵中的源级噪声,主要处理方法有一次降噪和二次降噪,其一次降噪是减少流体脉动和泵振动。二次降噪是使用阻尼材料,消除流体脉动并阻断泵内部振动的传递路径,以此影响流体传播(FBN)和结构传播噪声(SBN)。
Ganesh 和Ivantysynova[4]采用CASPAR 研究了配流盘结构对压力流量脉动、斜盘上力矩和容积效率的影响,介绍了柱塞腔内增压和减压速率与压力流量波动和斜盘上力矩等因素的相关性。Pelosi和Ivantysynova[5]基于一完全耦合计算模型,研究传热和热弹性变形问题,讨论液压油弹性变形、温度效应对柱塞泵摩擦副润滑机理的影响。Ye 等[6]为捕捉空气释放和空化现象,利用阻尼孔的新型阀板开发了动态泵模型,基于该模型和多目标遗传算法研究阀板参数对噪声源影响,降低了轴向柱塞泵的噪声。Zhou 等[7]以轴向柱塞机械滑靴/斜盘界面润滑油膜厚度为测量参数,对滑靴在不同负载压力、转速和充油压力下的姿态进行了实验研究。Ye 等[8]建立了弹性流体力学模型,分析了不同转速和载荷压力下的滑靴承载能力,研究了倾斜角度、面积密度、凹坑深径比和操作条件等因素的综合影响。
任博等[9]采用Kriging 和蒙特卡洛方法,分析柱塞泵结构系统可靠性,并建立各部件故障模型,基于累积分布函数计算其误差。叶绍干等[10]重点考虑配流盘油膜特性的影响,采用多目标遗传算法对油膜润滑相关参数进行分析计算。郭一谚等[11]通过T-S 模型和大数据得到PID 控制算法的模糊控制,提高系统的动态控制性能,实现高精度和快控制柱塞泵排量的目的。徐孜等[12]为能够精确识别轴向柱塞泵中发生的气穴等级,采用粒子群算法,对泵出口压力信号采集进行预评估,通过对采集信号迭代处理获取重点信号分量,将其重新构造实现空穴等级的识别,同时实验验证了该理论的有效性。张延君等[13]为解决轴向柱塞泵在工作过程中产生的振动、噪声等问题,将配流盘的阻尼结构改为三角槽,计算该结构不同时刻的过流面积,并对泵进行可视化数值研究,分析三角槽结构参数对柱塞腔内压力流量脉动的影响。索晓宇等[14]为验证流量脉动与流量谷值和峰值的相关性,分析柱塞腔内压力腔内流量倒灌对流量谷值和峰值的影响,并改变配流盘减振槽来降低流量倒灌、腔内压力的发生,从而达到抑制空穴的目的,同时增加了柱塞泵的容积效率。黄家海等[15]将线性化与降阶方法相结合,通过试验和AMESim 验证了对VDAAPP 频响和斜盘力矩的影响因素计算。姜晓天等[16]运用多目标算法和iSIGHT 优化平台,计算并优化阀板中U 型槽的相关参数对柱塞腔内压力和出口流量脉动的影响。
本研究基于正交试验、Kriging 曲面插值以及遗传粒子群算法结合,得到柱塞泵多影响因素的最优参数,最终将最优解导入多学科计算平台AMESim,根据柱塞泵进油口处气穴的产生,评价优化过程的可靠性。
1 计算模型
1.1 柱塞运动
图1所示的是轴向柱塞运动示意图。
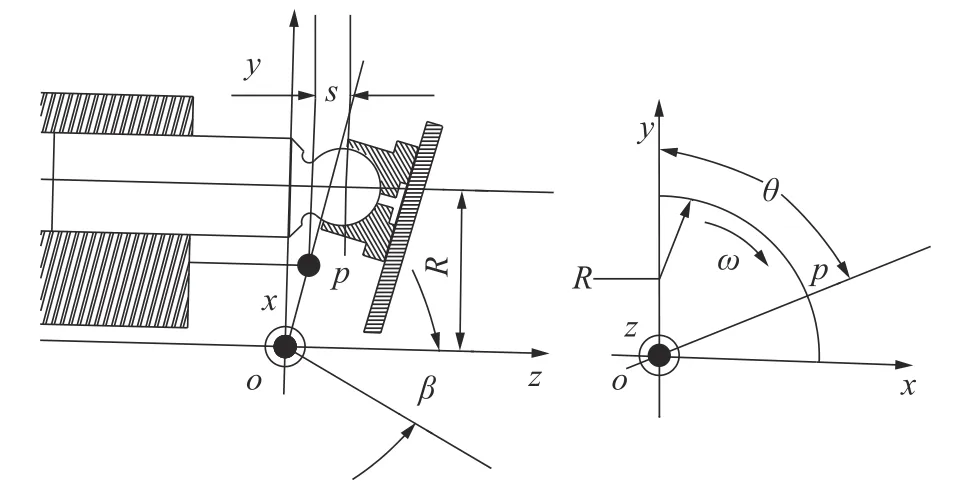
图1 轴向柱塞运动示意图Fig.1 Schematic diagram of axial plunger movement
当柱塞随轴在z轴上以恒定的角转速 ω旋转时,柱塞在z轴方向的速度为
式中:R为柱塞分布圆半径;β为斜盘倾角;θ 为缸体转角。
1.2 柱塞腔压力
轴向柱塞泵腔内压力Pi是由各柱塞腔控制容积中进入和排出的流量叠加所得,其表达式[17]为
式中:βe为油的体积模量;Vpci为柱塞腔的控制体积;Qlpi和Qhpi分别为柱塞腔与进出口间的流量;Qli为柱塞腔的泄漏流量。
柱塞腔压力与进出口间的流量可表示为:
式中:C为流量系数;Pl和Ph分别为进出口中的压力;Alpi和Ahpi分别为柱塞腔与进出口间的过流面积;ρ为油液密度。
1.3 泵的进出口流量
为了解泵中流量脉动,通过将各柱塞腔内进入或排出流量相加,得出进出口流量表达式分别为:
1.4 斜盘力矩
轴向柱塞泵的振动来自于内部的压力流量脉动和斜盘力矩,斜盘上受力如图2所示。
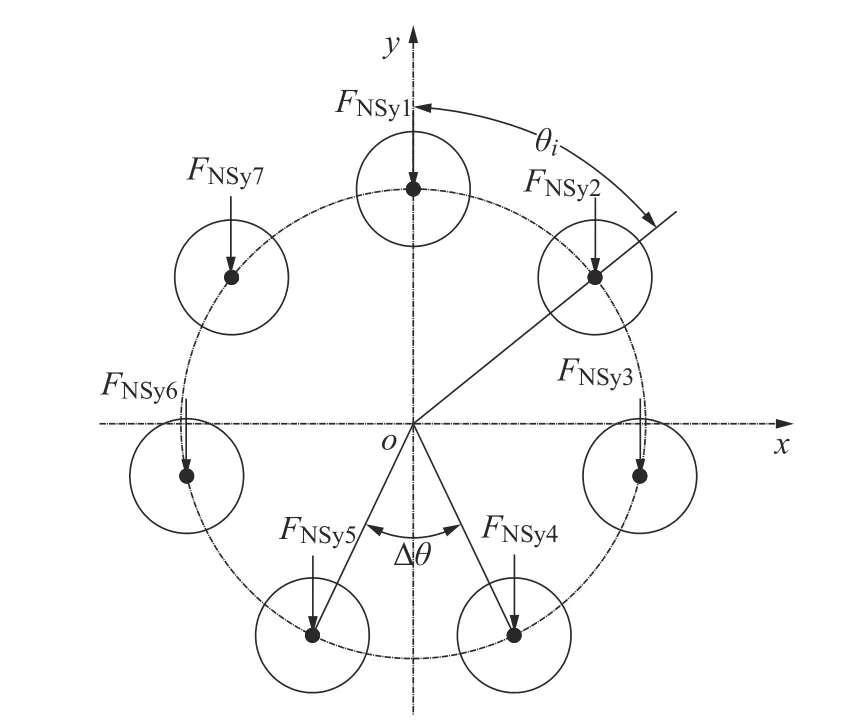
图2 施加在斜盘上的外力Fig.2 External force on swashplate
其中斜盘力矩是通过将各柱塞腔内压力作用在斜盘上叠加而得,其中惯性力和摩擦力远小于Pi而忽略不计,表达式为
式中:Z为柱塞数量;FNSy为柱塞腔内压力。
2 正交试验分析工艺参数
2.1 柱塞泵的气穴影响因素
正交试验的目的是对柱塞泵中进油口处气穴成形问题进行研究。本研究将柱塞转速、柱塞直径、油液中含气量和进油口压力梯度这些因素作为结果输出,得到正交试验评价指标。在优化过程中,设计变量的取值关系到最优解或者次优解,完成影响因素取值范围确定,因素水平表表1所示。
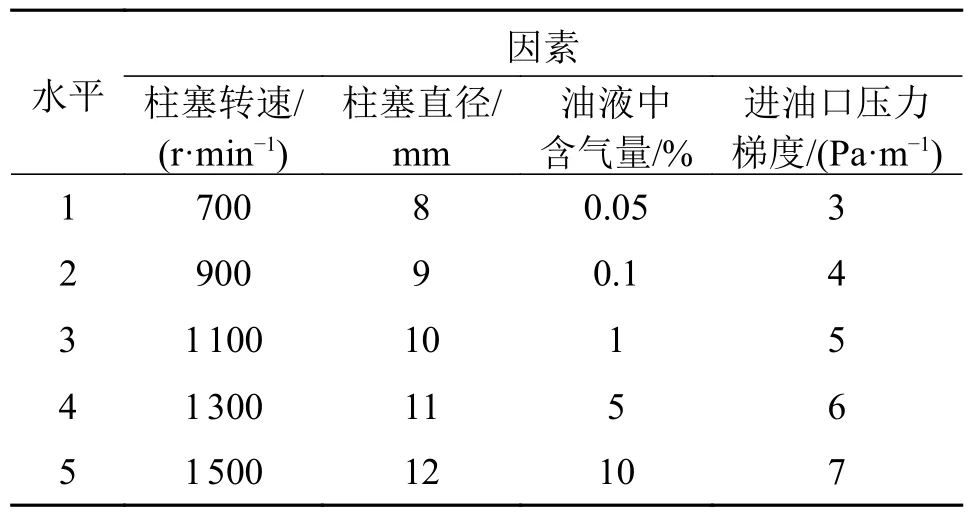
表1 因素水平表Tab.1 Factor level
2.2 正交试验设计表
运用SPSS 数据统计分析软件,基于表1中因素与水平,得出正交试验表如表2所示。柱塞转速、柱塞直径、油液中含气量和进油口压力梯度是影响柱塞泵气穴的主要参数,第2~5列分别为不同参数的排列组合,其各因素排列为A1B1C1D1。

表2 正交试验表Tab.2 Factor level
2.3 正交试验结果分析
运用AMESim 软件,建立的单柱塞泵计算模型如图3。分析各参数对柱塞腔内压力和出口流量的影响,根据实际工况要求,进行25组不同参数的计算,柱塞腔内压力和出口流量试验结果见图4。
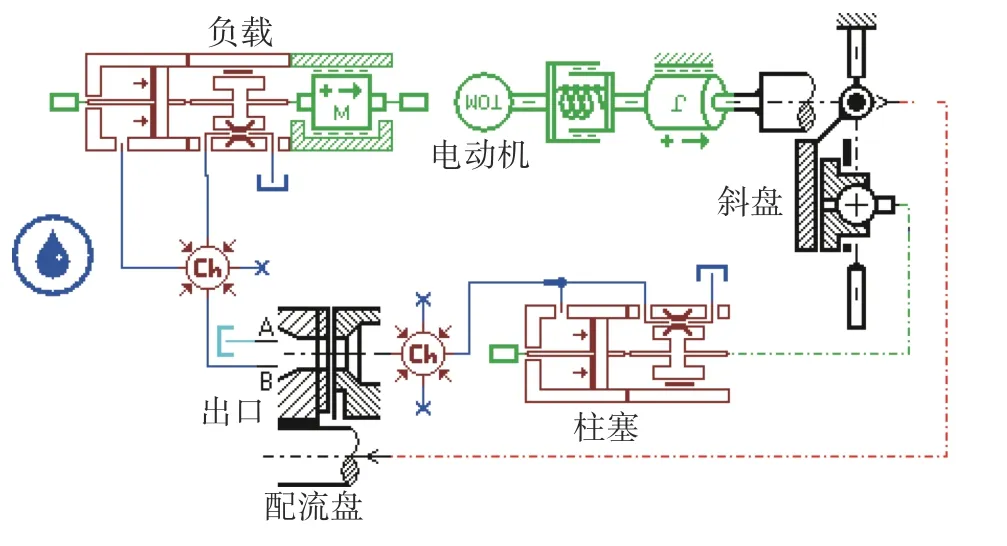
图3 AMESim 单柱塞泵仿真模型Fig.3 AMESim single piston pump simulation model

图4 不同水平下柱塞腔内压力和出油口流量Fig.4 Pressure in piston cavity and oil outlet flow at different levels
为分析不同因素在试验结果中的重要程度,利用方差分析,将计算结果的总平方和以及自由度分解为不同因素所对应的平方和及自由度。所有观察值总平方和分解表达式[18]为
式中:k为水平数;n为每个水平数所对应的观察值;xij为第i个水平的第j个观察值;为第i个水平所有观察平均值;为所有观察平均值。
自由度的分解表达式[19]为
式中:fT为总观察值个数减1;f1为水平数减1;f2为因素数减1。
把柱塞腔内压力和出油口流量作为因变量,运用多因素方差分析各因素对因变量的显著性,设置显著性水平值为0.05。由表3可知,因变量为柱塞腔内压力时,油液中含气量、柱塞转速和柱塞直径的显著性值小于0.05,说明对柱塞腔内压力影响较大,相反,进油口压力梯度显著性值大于 0.05,则对柱塞腔内压力影响小。因此,各因素对柱塞腔内压力的显著性为 C>A>B>D,即油液中含气量>柱塞转速>柱塞直径>进油口压力梯度。对于因变量出油口流量,柱塞转速、柱塞直径和油液中含气量的显著性值小于0.05,对出油口流量影响较大,而进油口压力梯度显著性值大于0.05,得出各因素对出油口流量的显著性为 A>B>C>D,即柱塞转速=柱塞直径>油液中含气量>进油口压力梯度。

表3 多因素方差分析检验结果Tab.3 Test results of one-way ANOVA
式中:y(x)为因素x的回归多项式;β为回归系数;z(x)为高斯相关函数,即表达式[21]为
式中:n为因素数量;为因素x的第n-1个分量;θm为相关参数θ 的第m个分量。
针对表3的方差分析检验结果,因素A、因素B 和因素C 的组合参数分析,以柱塞腔内压力及出油口流量作为目标函数,建立Kriging 模型,得出因素C 和A 或因素A 和B 与目标函数的可视化曲面,如图5和图6所示。通过分析,随着柱塞转速和柱塞直径的增加,柱塞腔内压力升高,出油口流量增加,同时油液中含气量为2%,致使柱塞腔内压力的变化最大。
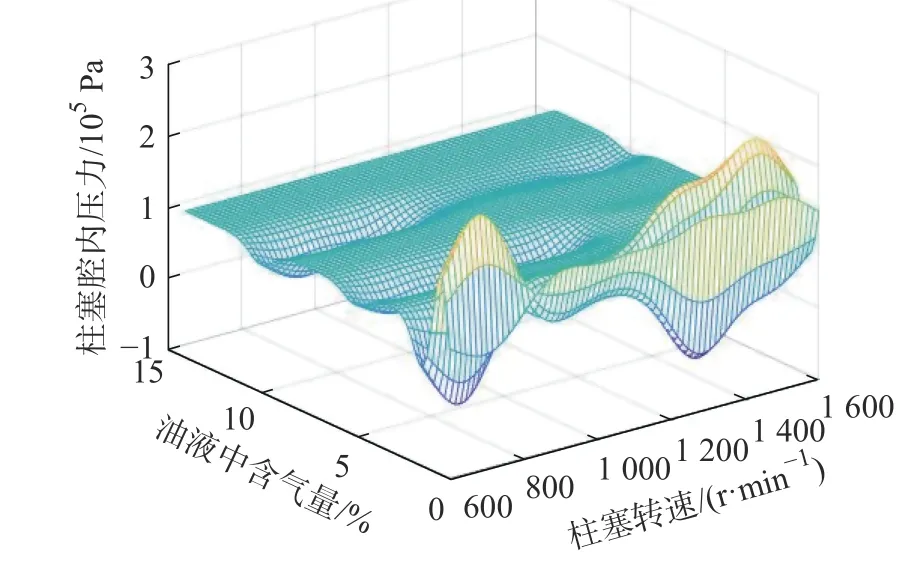
图5 因素C 和A 的Kriging 插值拟合Fig.5 Kriging interpolation fitting of factors C and A

图6 因素A 和B 的Kriging 插值拟合Fig.6 Kriging interpolation fitting of factors A and B
3 遗传粒子群算法的优化设计
为提高解的有效性,通过比较遗传算法(GA)和粒子群算法(PSO)的个体选择和操作过程,将两者以串并联的方式组合成遗传粒子群算法。根据正交试验与方差分析,其优化目标为柱塞转速、柱塞直径和油液中含气量,约束条件为柱塞腔内压力和出油口流量。为得到各优化目标的最优结果,采用遗传粒子群算法,对其进一步优化,设群体大小为300,迭代次数为500。图7为柱塞腔内压力最优解,得出各因素最优参数:柱塞转速为710 r/min,柱塞直径为8.2 mm,油液中含气量为2.9%,所对应柱塞腔内压力47 991 Pa。图8为出油口流量最优解,得出各因素最优参数:柱塞转速为694 r/min,柱塞直径为7.8 mm,油液中含气量为3.1%,所对应出油口流量为2.1 L/min。综合柱塞腔内压力与出油口流量下的最优解,取最优参数柱塞转速700 r/min,柱塞直径8 mm,油液中含气量3%。

图7 种群均值及柱塞腔内压力最优解Fig.7 Optimal solution of population mean and pressure in piston cavity

图8 种群均值及出油口流量最优解Fig.8 Optimal solution of population mean and oil outlet flow
针对最优参数进行计算,得到柱塞腔内压力及出油口流量变化,如图9所示,可看出柱塞腔内负压为-29 573.5 Pa,其腔内最大与最小压力差为47 987 Pa,出油口流量2.18 L/min,无气穴现象发生。
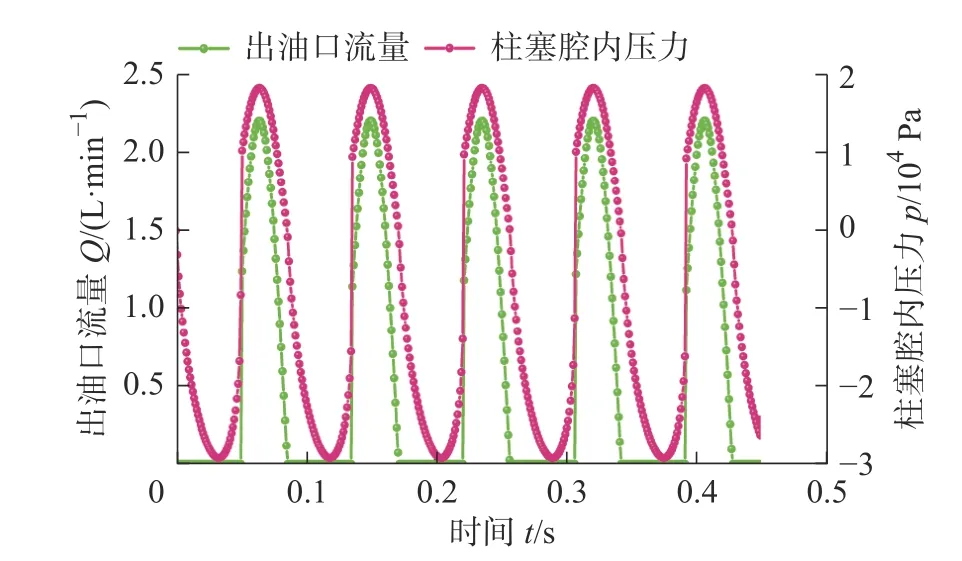
图9 优化后的柱塞腔内压力及出油口流量Fig.9 Optimized pressure in plunger cavity and oil outlet flow
4 结论
通过分析柱塞转速、柱塞直径、油液中含气量以及进油口压力梯度对气穴的影响,基于正交试验和Kriging 模型,提出优化方案,采用遗传粒子群算法对柱塞转速、柱塞直径、油液中含气量进行优化,得出以下结论:油液中含气量、柱塞转速和柱塞直径的显著性值均小于0.05,对柱塞腔内压力和出油口流量影响较大;经优化,柱塞转速700 r/min,柱塞直径8 mm,油液中含气量3%,抑制了气穴发生。
