EC模式和GFS模式对黄渤海10 m风速预报性能对比分析

王彬，李文博*，李锐，侯乔琨，孙雅文，刘桂艳

（1.自然资源部北海预报减灾中心，山东青岛266100；2.山东省海洋生态环境与防灾减灾重点实验室，山东青岛266100）

0 引言

黄渤海全年受冷空气、气旋（包括温带气旋和热带气旋）以及两者的配合影响，海面易出现大风天气，对船舶航行、海洋捕捞以及海上石油开发等活动造成严重影响，因此对黄渤海海面风的准确预报需求非常迫切。

早期海面风的预报以经验预报和统计预报为主，近年来随着计算机技术的发展，数值预报逐渐成为海面风预报的主要工具[1-4]。欧洲中期天气预报中心（European Centre for Medium-Range Weather Forecasts，ECMWF）的细网格产品（简称EC）和美国国家环境预报中心（National Centers for Environmental Prediction, NCEP）的全球预报系统（Global Forecasting System）风速预报产品（简称GFS）是目前常用的两种高分辨率气象数值产品，两种预报分别使用四维变分和集合卡尔曼滤波的同化技术，预报准确度较高。已有一些学者对两种产品的海面风预报进行了检验和分析，例如吴俞等[5]利用南海4个海岛站的观测数据，对EC 模式10 m 风场预报产品的误差进行了分析，指出EC 模式预报存在季节性的偏差；方艳莹等[6]利用浙江沿海10 m 风的观测结果，对EC 模式细网格产品的预报性能进行了评估，指出不同天气系统下EC 模式的表现有所差异；于鑫等[7]基于EC 模式细网格产品对南海北部的预报能力进行了检验分析，结果表明EC模式对5级及以下风的预报效果较好；连喜虎等[8]基于黄渤海浮标观测，对EC 模式预报的10 m 风速和风向进行了检验，发现EC 模式产品在黄海中部预报效果最佳，模式与实测风速相关性较好；DE CHIARA 等[9]评估了EC模式在同化卫星资料后对海面10 m风场的预报改进情况，指出同化后海面10 m 风速的标准偏差约为1.25 m/s；HAIDEN 等[10]利用2003—2021 年欧洲气象观测站的数据，计算得到60 h 和72 h EC 模式的10 m 风速预报的均方根误差为2～3 m/s，平均偏差为-0.5～1 m/s；周荣卫等[11]利用气象站和测风塔的实测风速序列，检验得到在我国沿海尤其是南部沿海地区EC 模式预报风场优于GFS 模式。相比而言，针对GFS 模式的海面10 m 风检验工作较少，黄渤海海域两种模式的对比分析更加缺乏。

为了更好地开展黄渤海海上大风的预报服务，本研究拟利用EC 模式和GFS 模式数值预报产品，对黄渤海10 m 风进行预报评估和对比分析，以期为预报员在实际预报中释用这两种数值模式产品提供参考，从而提高海面风预报的准确率。

1 数据与方法

1.1 数据整理

本文选取黄渤海10 个浮标和5 个海洋站数据作为观测结果，对EC模式和GFS模式24～72 h（24 h预报性能指模式前24 h 预报的平均计算结果）的10 m 风速预报性能进行对比检验。渤海包含MF01001、MF01002 和MF01004 浮标（分别位于辽东湾口、渤海中部和莱州湾口）以及东营港和龙口2个海洋站，渤海海峡包含MF02001和MF02002浮标（均位于海峡中部），黄海北部包含MF02004 浮标（位于成山头东北方向的外海海域）和小长山海洋站，黄海中部包含MF03003（位于千里岩附近）、MF03005、MF03006和MF03007浮标（3个浮标均位于黄海中部的南部海域，按顺序自西向东排列）以及日照港和小麦岛两个海洋站。

使用的资料包括：①2021 年1—12 月浮标和海洋站的3 h 间隔风速观测（原始观测为1 h 间隔，这里为了与模式产品保持一致，人为处理成3 h 间隔，并使用风速高度换算公式将其换算成海面10 m 风速[12-13]）；②20时（世界时，下同）起报的EC模式10 m风速预报产品（空间分辨率为0.125°×0.125°，时间分辨率为3 h），GFS 模式10 m 风速预报产品（空间分辨率为0.25°×0.25°，时间分辨率为3 h）。EC 模式和GFS 模式预报数据利用双线性插值方法插值到浮标和海洋站站点。所有数据均通过严格的质量控制，GFS 模式和海洋站观测数据的缺测率为0，EC 模式和浮标观测数据有部分日期缺失并包含一些奇异值，整理后的缺测率较低（5%左右）。

1.2 误差统计方法

相对误差（Er，单位：%）反映了预报偏离观测的相对程度。计算公式为：

均方根误差（Erms，单位：m）反映了预报偏离观测的离散程度。计算公式为：

平均偏差（Ebias，单位：m）反映了预报相对于观测的整体偏离程度。计算公式为：

2 结果与分析

2.1 误差总体情况

图1 为24～72 h 两种模式的均方根误差，误差范围为1.75～2.35 m/s。随着预报时效的增长，预报效果逐渐变差，EC模式48 h和72 h风速预报的均方根误差分别比24 h 增大了14.3%和25.7%，GFS 模式分别增大了15.5%和25.7%。横向对比来看，EC模式对10 m 风速的预报效果优于GFS 模式，24～72 h 的均方根误差比GFS 模式减小了6.8%～8.0%。从相对误差来看（图略），虽然由于部分观测值较小导致相对误差较大（均大于47%），但EC 模式预报的相对误差优于GFS模式。图2为两种模式的偏差箱线图，用来体现不同预报时效下预报偏差的离散程度和数据的集中趋势[14]。EC 模式24～72 h 风速预报偏差中位数为0.19～0.25 m/s，GFS 模式为0.33～0.41 m/s，两种预报产品风速的预报结果整体略偏大，EC 模式的偏离程度更小，而且两种模式预报偏差离散度随着预报时效的增长而不断增大。整体来看，两种模式对10 m 风速的预报都具有较高水平，EC模式的预报效果更优。

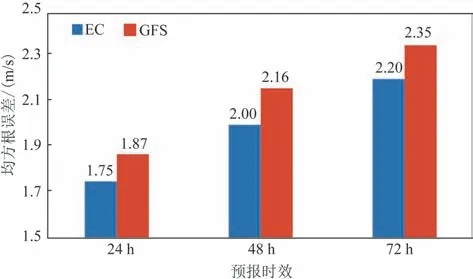
图1 EC模式和GFS模式24～72 h预报的均方根误差Fig.1 EC and GFS model's root mean squared error of 24～72 h prediction

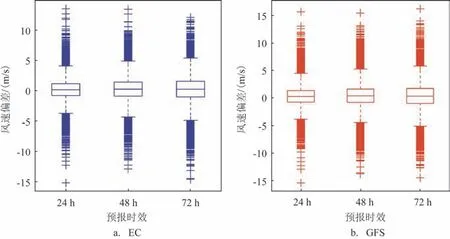
图2 EC模式和GFS模式24～72 h预报偏差箱线图Fig.2 EC and GFS model's box diagram of 24～72 h prediction

从24 h（48～72 h 结果类似，故省略）不同风速的预报误差来看（见图3a），EC 模式的相对误差在6级风的预报时最小，为13.09%，之后逐渐变大，8 级及以上风的预报误差明显增大（相对于7 级风增大41.8%），这可能是因为模式对极大值的预报偏弱；GFS 模式的相对误差在7 级风的预报时表现最好，为10.16%；EC模式对于5级及以下风的预报结果好于GFS 模式，更大风速下GFS 模式的预报效果更佳。两种模式的均方根误差整体呈现随风速增加而逐渐增大的趋势（见图3b），8 级及以上风的预报的均方根误差明显上升（EC 模式增大63.5%，GFS模式增大53.7%），EC模式在5级风的预报的均方根误差表现最好，为1.65 m/s，GFS 模式在4 级风时表现最好，为1.86 m/s，EC 模式在5级及以下风的预报效果比GFS 模式更好，GFS 模式对6 级及以上风的预报更佳。两种模式对4级及以下风的预报整体偏大0.52～0.57 m/s，对5 级及以上风的预报偏小，偏离程度随风速增加而逐渐增大，EC模式的偏差大于GFS 模式。总体来说，EC 模式对5 级及以下风的预报效果好于GFS 模式，而GFS 模式对6 级及以上风的预报效果更优。

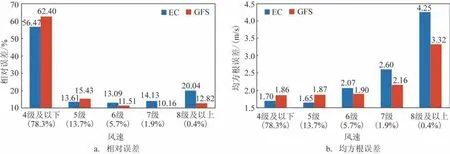
图3 不同风速条件下EC模式和GFS模式24 h预报的相对误差和均方根误差Fig.3 EC and GFS model's relative error and root mean squared error of 24～72 h prediction under different wind speed

在日常的预报业务中，5 级及以上风的天气过程更值得关注，因此2.2 和2.3 节选取5 级及以上风的观测风速作为对比，对两种模式的时空特征以及强天气过程的表现进行分析。

2.2 误差时空分布

图4为两种模式所有观测站点的泰勒图。泰勒图是由TAYLOR[15]于2001年首先提出，近年来被广泛应用于模式评估与检验。基于余弦定理，泰勒图巧妙地将模式的相关系数、中心均方根误差和标准差之比3个评价指标整合在一张极坐标图上。图中从圆点出发的径向距离表示模式与观测的标准差之比，比值越接近1，表示预报能力越好；中心均方根误差是以观测点为圆心的半圆弧，模式点越靠近观测点，表明预报越接近观测值；相关系数由方位角的余弦决定，当模式预报结果与观测值较一致时，相对系数越接近1。从图4 可以看出，GFS 模式和EC 模式数据在黄海中部最远离陆地的MF03007站的误差最小，而小长山站的两种海面风场产品的误差都较大，说明两种模式对MF03007 站的预报效果最好，对小长山站的预报效果最差。两种模式在近岸海洋站的预报效果比浮标站差很多，尤其是小长山、小麦岛和日照港的预报效果远远低于其他站点，3个站的中心均方根误差都大于1.2 m/s，标准差之比均大于1.3，相关系数均小于0.5，这可能与3 个站的地理位置有关（北侧均为陆地）。此外，通过两种海面风场产品的对比发现，整体上EC 模式的标准差预报效果更好，中心均方根误差也优于GFS 模式，而两个模式的相关系数比较接近。

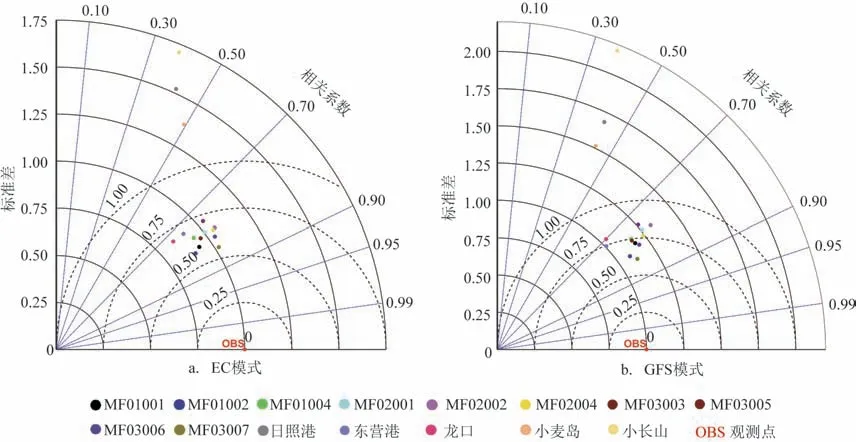
图4 EC模式和GFS模式24 h预报的泰勒图Fig.4 EC and GFS model's Taylor diagram of 24 h prediction

为进一步分析两种模式的时空预报差异，图5给出外海、近岸以及不同海区（选取海上浮标站作为海区的代表，可以排除近岸海洋站的影响）两种模式的风速预报均方根误差对比。从图中可以看出，两种模式在近岸的预报误差均远高于外海，EC模式在外海的均方根误差比近岸减小53.7%，GFS模式减小51.1%；两种模式在外海和近岸的预报水平比较接近，EC模式在外海略好，GFS模式在近岸略好；EC模式在黄海中部的预报误差最小（1.51 m/s），之后依次为渤海海峡、黄海北部和渤海，GFS 模式同样对黄海中部的预报效果最好（1.53 m/s），其次为黄海北部、渤海海峡和渤海；GFS 模式在渤海的预报效果好于EC 模式，其他海区则EC 模式的预报效果更好。

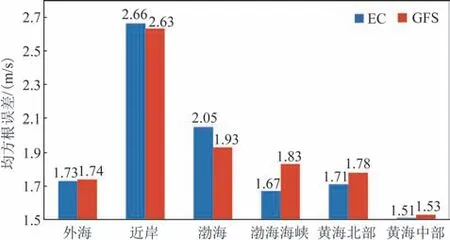
图5 不同区域EC模式和GFS模式24 h预报的均方根误差Fig.5 EC and GFS model's root mean squared error of 24 h prediction in different areas

图6 为两种模式在不同月份的风速预报误差。从图中可以看出，两种模式的误差在1—8月整体呈上升趋势，8 月EC 模式的均方根误差最大，为2.89 m/s，GFS 模式最大误差为3.11 m/s，9—12 月误差逐渐减小，12 月EC 模式的误差最小，为1.61 m/s，GFS模式最小误差为1.51 m/s。横向对比，EC 模式风速产品在4—8月的预报效果好于GFS模式，其他月份则GFS 模式的预报效果更好，造成这种差异的原因可能与模式对不同天气过程的预报效果有关。

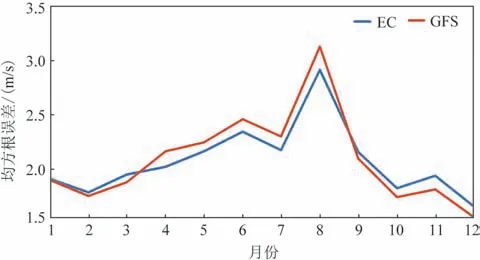
图6 不同月份EC模式和GFS模式24 h预报的均方根误差Fig.6 EC and GFS model's root mean squared error of 24 h prediction in different months

2.3 强天气过程表现

考虑到两种模式对不同月份预报效果的差异，本研究挑选了2021年的强天气过程进行预报检验。结合日常业务预报要求，定义当黄渤海海区中不少于两个站点的风速≥6级、至少有1个站点连续两个时次的风速≥6级且至少有1个站点的有效波高＞2 m时，即为1次强天气过程。

经统计（见表1），2021 年黄渤海海区的强天气过程共有38 次，其中冷空气过程18 次，气旋过程10次，冷空气和气旋配合过程10 次。结合李培顺等[16]对影响黄渤海海区的强天气过程的分类，将冷空气过程划分为西北路、北路和西路，其中西北路冷空气最多，有14 次，北路3 次，西路最少，只有1 次，集中分布在1—3 月和10—12 月，影响范围一般是黄渤海整个海区，有3 次西北路冷空气仅影响渤海海区；按气旋过程可划分为渤海气旋、黄河气旋、江淮气旋和台风4 种，其中渤海和江淮气旋最多，各占4次，黄河气旋和台风过程各有1次，集中分布在4—9月，50%的气旋过程影响范围仅仅覆盖黄海，另外50%的影响范围是整个海区；按冷空气与气旋的配合可分为西北路冷空气和黄河气旋（3 次）、西北路冷空气和江淮气旋（5 次）、北路冷空气和江淮气旋（1次）以及北路冷空气和台风（1次），该类过程全年均有分布，影响范围一般是整个海区，仅有1次西北路冷空气和黄河气旋的配合过程影响范围是渤海。

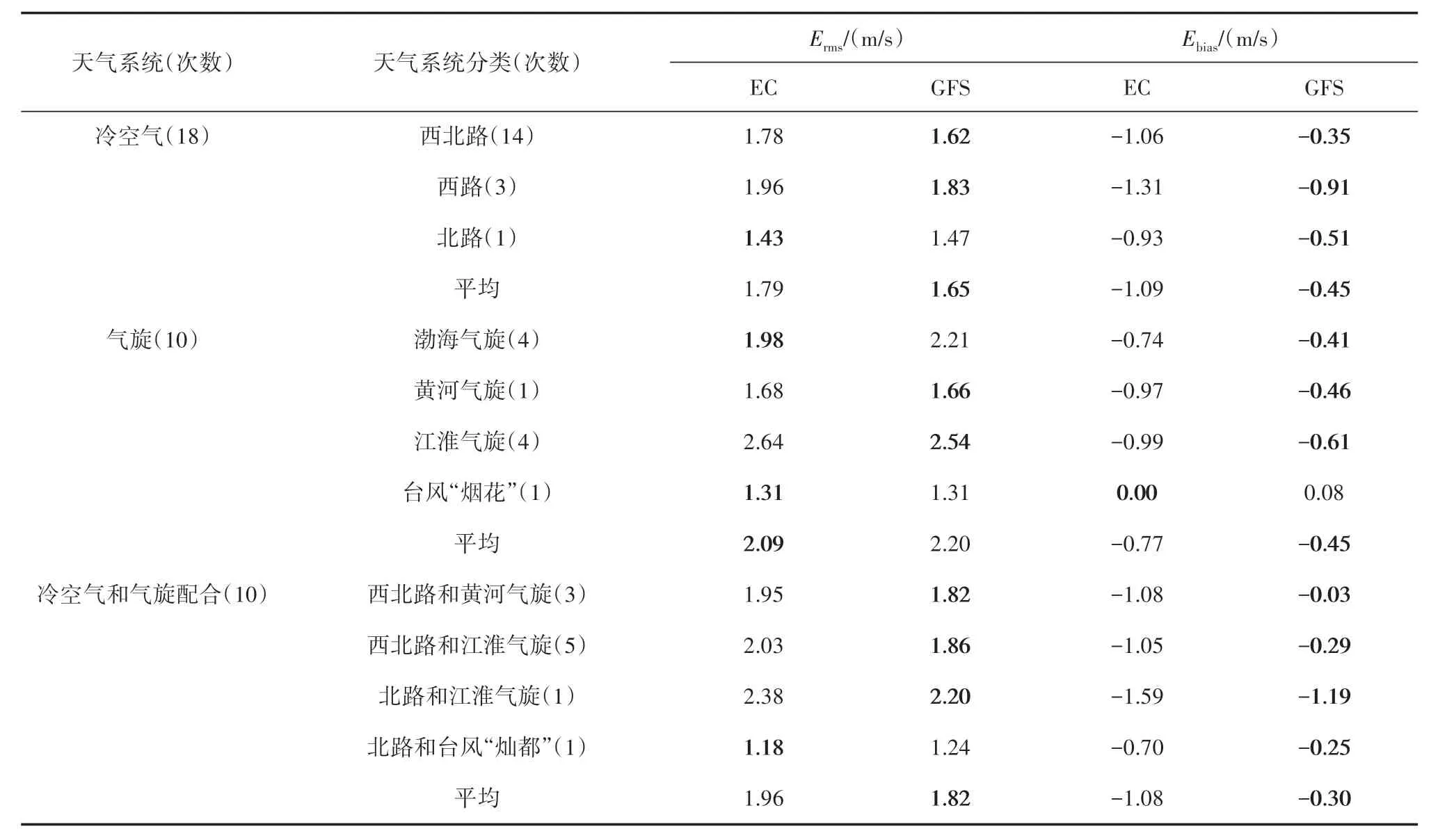
表1 24 h不同天气系统影响下的强天气过程预报评分Tab.1 24 h forecast scores of strong weather processes under different weather systems

计算发现，随着预报时效的增加，风速预报误差逐渐增大。两种模式对冷空气的预报表现相对稳定，48 h 和72 h 风速预报的均方根误差平均增大14%和28%，气旋预报误差增大最为明显，其中EC模式的均方根误差和平均偏差分别增大了21%和30%，GFS 模式分别增大了32%和54%。结合表1进一步分析，对于冷空气影响下的强天气过程，GFS模式的预报评分明显好于EC 模式，仅在5 次过程（西北路3次，北路和西路各1次）中EC模式的预报评分超过GFS 模式。24 h EC 模式风速预报的平均均方根误差为1.79 m/s，GFS 模式为1.65 m/s，造成这种差异的原因可能是模式对冷空气的强度预报不足，其中EC模式风速预报平均偏低1.09 m/s，GFS模式平均偏低0.45 m/s。对于气旋影响下的强天气过程，两种模式对黄河气旋以及台风“烟花”的预报结果基本一致，EC模式对渤海气旋的风速预报效果更好，平均均方根误差为1.98 m/s，GFS 模式为2.21 m/s。对于江淮气旋的预报，两种模式各有优劣，例如对于7 月2 日的江淮气旋，GFS 模式的预报效果优于EC模式（EC 模式风速预报的均方根误差为3.11 m/s，GFS 模式为2.46 m/s），对于8 月23 日的江淮气旋，EC 模式的预报效果更优（EC 模式风速预报的均方根误差为2.51 m/s，GFS模式为3.25 m/s）。从结论中我们能够发现（图略）预报路径的偏差是导致评分差异的主要原因，平均来看，EC模式对气旋风速预报的效果略优于GFS模式，均方根误差分别为2.09 m/s和2.20 m/s，模式对气旋强度的预报多偏弱，EC 模式平均偏低0.77 m/s，GFS 模式平均偏低0.45 m/s，仅有一次渤海气旋出现了预报偏强的情况。对于冷空气和气旋配合影响下的强天气过程，GFS 模式的评分好于EC 模式，仅有两次过程（西北路和黄河气旋配合1 次，北路和台风“灿都”配合1 次）的EC 模式评分更好，GFS 模式风速预报的平均均方根误差为1.82 m/s，EC 模式为1.96 m/s，GFS 模式预报平均偏弱0.30 m/s，EC模式平均偏弱1.08 m/s。

3 结论

本研究收集整理了2021年EC模式和GFS模式的10 m 风速数值预报产品以及黄渤海浮标和海洋站的风速观测数据，通过比较模式数据和观测数据，统计分析了多种误差指标。主要结论如下：

①两种模式对10 m 风速的预报都具有较高的水平，24 h预报的均方根误差小于1.9 m/s，能够为业务化预报提供参考。随着预报时效的增长，预报效果逐渐变差，48～72 h 预报的均方根误差比24 h 增大了15%和26%，EC模式24～72 h风速预报的偏差中位数为0.19～0.25 m/s，GFS模式为0.33～0.41 m/s，两种预报产品的风速预报结果整体略偏大，EC模式的偏离程度更小。EC 模式的整体预报效果优于GFS 模式，24～72 h 预报的均方根误差比GFS 模式减小了6.8%～8.0%。

②对于不同风速的预报，EC模式预报的相对误差在6 级风时表现最好，GFS 模式在7 级风时表现最好，两者的均方根误差整体呈现随风速增加而逐渐增大的趋势。EC 模式对5 级及以下风的预报效果好于GFS 模式，GFS 模式对6 级及以上风的预报效果更好。

③对于5级及以上风的24 h预报，从空间上看，两种模式对小长山站的预报效果最差，对黄海中部MF03007 站的预报效果最好，外海区域预报的均方根误差比近岸减小50%以上，两种模式对黄海中部的预报效果最好，对渤海的预报效果最差。两种模式对外海和近岸的预报效果比较接近，GFS 模式在渤海的预报效果好于EC 模式，而在其他海区EC 模式的预报效果更好。从时间上看，两种模式的预报误差在1—8 月整体呈上升趋势，9—12 月误差逐渐减小，EC 模式风速产品在4—8 月的预报效果好于GFS模式，其他月份则GFS模式预报效果更好。

④在强天气过程方面，随着预报时效的增长，GFS 模式的气旋预报出现误差急剧增大的现象。GFS 模式对冷空气的风速预报效果好于EC 模式，两者的均方根误差分别为1.65 m/s 和1.79 m/s；EC模式对渤海气旋的风速预报误差为1.98 m/s，优于GFS 模式的2.21 m/s，而对江淮气旋来说，不同过程下两种模式各有优劣；GFS 模式对冷空气和气旋的配合过程的风速预报误差为1.82 m/s，好于EC 模式的1.96 m/s。模式误差的来源主要是气旋预报的路径偏差以及对冷空气强度的预计不足，EC模式对冷空气的风速预报平均偏弱1.09 m/s，GFS 模式平均偏弱0.45 m/s。