不同海浪数值预报产品在渤海和黄海的预报水平评估

李文博，李锐*，王彬，张薇，高山，侯乔琨，孙雅文

（1 山东省海洋生态环境与防灾减灾重点实验室山东青岛266100；2 自然资源部北海预报减灾中心山东青岛266100）

0 引言

海浪灾害是人类在海上和近岸活动的最主要威胁，对生命和财产安全可能造成巨大损害[1-5]，因此，准确的海浪预报是海上活动的最基本保障。随着数值预报技术的发展、数值预报产品的丰富和改进以及计算机运算能力的提高，以海浪数值模式为核心的海浪数值预报系统已成为海浪预报和业务研究的主要手段，海浪预报水平也有了较大提高［6-9］。目前常用的海浪预报数值模式主要为第三代海浪数值模式WAM[10-12]和WAVEWATCH-Ⅲ[13-15]，两种模式均可模拟大洋和近海的海浪生成、传播与耗散过程。

随着海浪数值预报产品的广泛应用，对其预报误差的系统检验也必不可少。目前已有不少学者在海浪数值预报产品的评估方面做出研究。20 世纪 末21 世 纪 初，TOLMAN 等[16-18]通 过 对 比WAVEWATCH-Ⅲ模式计算结果与浮标数据，改进了模式源函数；BIDLOT[19]对21 a 的数值预报结果进行检验评估，发现包括欧洲中尺度天气预报中心（European Centre for Medium - Range Weather Forecasts，ECMWF）海浪预报产品（简称EC）在内的几种产品的预报准确性均有提高；WANG 等[20]首次利用中国近海的波浪浮标观测数据检验了EC海浪预报产品的误差，并分别从离岸距离、水深等方面讨论了EC 产品的误差分布情况；李燕等[21]对WAVEWATCH-Ⅲ在渤海的预报结果进行了检验；梁 小 力 等[22]对 基 于SWAN（Simulating Waves Nearshore）模式的全球海浪预报结果进行了初步验证。然而，目前的海浪数值预报产品评估仅限于对不同站位的误差开展统计，而对于误差的时空分布、尤其是不同天气过程下的误差分析却鲜有研究。另外，目前海浪预报水平评估主要聚焦于大洋和开阔海域，渤海和黄海作为半封闭海，海浪风区短、水深浅，与大洋海浪生成传播机制有较大不同，对现有海浪预报产品在渤海和黄海的预报能力缺少系统分析。为了系统评估渤海和黄海的海浪数值预报水平，本文拟对EC、美国国家环境预报中心（National Centers for Environmental Prediction，NCEP）的全球天气预报系统（Global Forecasting System）海浪预报产品（简称GFS）和自然资源部北海预报减灾中心（North China Sea Marine Forecasting Center of State Oceanic Administration）海浪预报产品（简称NMFC）在渤海和黄海海域的预报能力进行初步检验与评估，充分发挥数值预报产品在海洋环境预报中的作用，为今后渤海和黄海海浪预报技术发展提供有价值的参考。

1 资料与方法

1.1 数值预报产品

EC产品所用海浪模式为WAM。NMFC与GFS两种产品所用海浪模式均为WAVEWATCH-Ⅲ，其能量输入耗散项均采用ST4 参数化方案，其中NMFC主要参数化方案设置包括ST4风浪模型和海浪耗散项、JONSWAP 底部摩擦方法、线性风时间插值、三阶传播方案等。

考虑到资料的连续性，本文收集2021 年EC、GFS、NMFC 3 种预报产品24 h、48 h、72 h、96 h 预报时效的有效波高预报结果用于评估。EC 和GFS的时间分辨率为3 h，NMFC的时间分辨率包括3 h和1 h两种，其中3 h分辨率的NMFC用于与EC和GFS横向比较，1 h分辨率的NMFC用于日极值误差分析。各预报产品的简要情况介绍见表1。EC模式的整体预报效果优于GFS，其中24～72 h 的均方根误差（RMSE）比GFS减小了6.8%～8%，EC 24～72 h风速预报偏差中位数在0.19～0.25 m/s之间，GFS同类中位数在0.33～0.41 m/s之间，两种预报产品风速的预报结果整体略偏大，EC的偏离程度相对更小。

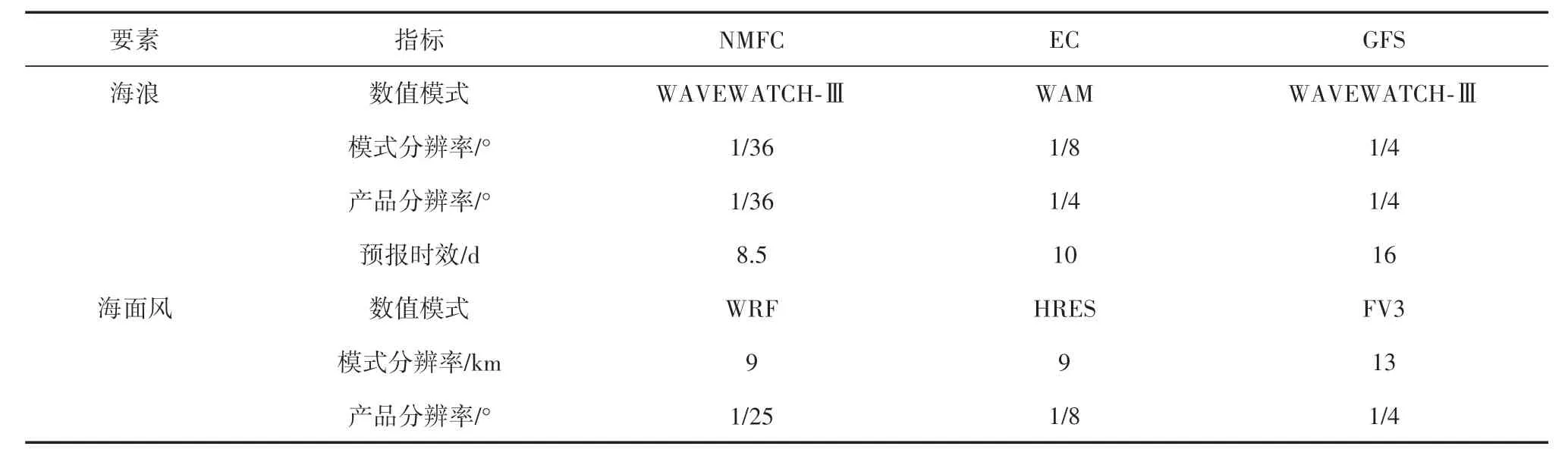
表1 各机构海浪数值预报产品及驱动风场情况Tab.1 Brief list of different ocean wave forecast products and wind forcing

1.2 观测资料

观测资料包括10 个10 m 大型海洋观测浮标以及5 个海洋站观测的2021 年有效波高数据，数据均通过严格的质量控制。渤海有3个浮标，位于119°～121°E，37.5°～40°N这一矩形海域内；渤海海峡有两个浮标，为南北分布；黄海北部有1 个浮标，位置约在该海域中心处；黄海中部有4个浮标，位于120°～124°E，35°～36.5°N 这一矩形海域内；5 个海洋站分别为东营港、小长山、龙口、小麦岛和日照港。观测结果分别与上述3 种海浪预报产品进行直接对比，并利用双线性插值将3种数值预报网格数据插值到观测站点进行误差统计。

1.3 误差统计方法

采用相对误差、均方根误差和平均偏差来评估数值预报产品偏离实际观测的情况，误差统计的具体方法如下：

①相对误差（Er，单位：%）反映了预报偏离观测的相对程度。计算公式为：

②均方根误差（Erms，单位：m）反映了预报偏离观测的离散程度。计算公式为：

③平均偏差（Ebias，单位：m）反映了预测相对于观测的整体偏离程度。计算公式为：

2 误差分析

2.1 误差总体分析

2021年3种预报产品到报率均超过95%。将预报产品24 h、48 h、72 h 和96 h 的有效波高预报数值插值到10 个浮标站位和5 个海洋站位，将所有结果与实测有效波高进行对比分析，并制作预报与观测数据对比图（见图1），其中红色线为利用最小二乘法拟合出的线（简称LSF 线），误差统计见表2。从图1 可以看出，渤海和黄海2021 年低于2 m 的有效波高出现概率超过60%，2 m 以上有效波高出现概率较小，最大有效波高超过5 m。从表2 可以看出，不同波高分段情况下EC 的RMSE 均为最低。3 m以上有效波高的预报相对误差、均方根误差和平均偏差均为EC最小，GFS最大，NMFC居中，三者24 h预报相对误差均在21%以下；3 m 及以下有效波高的预报均方根误差也是EC 最小，说明EC 对于海浪有效波高的整体预报水平高于NMFC 和GFS。从图1 的LSF 线和表2 平均偏差统计结果来看，3 种预报产品对于2 m 以上有效波高的预报结果整体偏小0.2 ～0.6 m，且GFS 大浪预报结果偏小的情况最为明显，这可能与现有海浪预报模式的风能输入参数化方案和参数设置更适用于开阔海域，渤海和黄海风区较短且波浪成长机制与开阔海域不同有关。

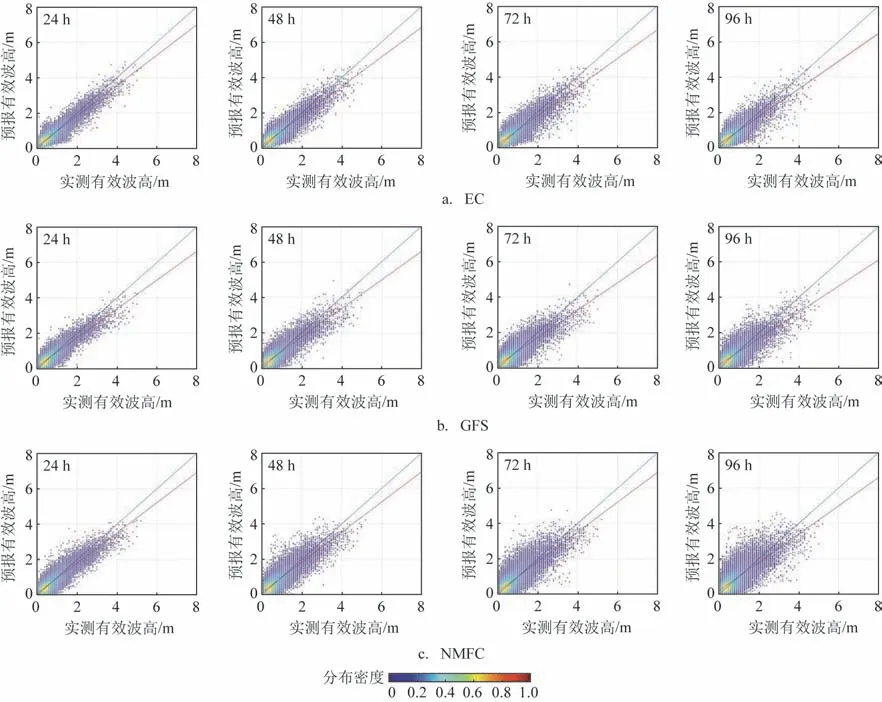
图1 预报有效波高与实测有效波高对比Fig.1 Comparison of significant wave height forecasts with observations

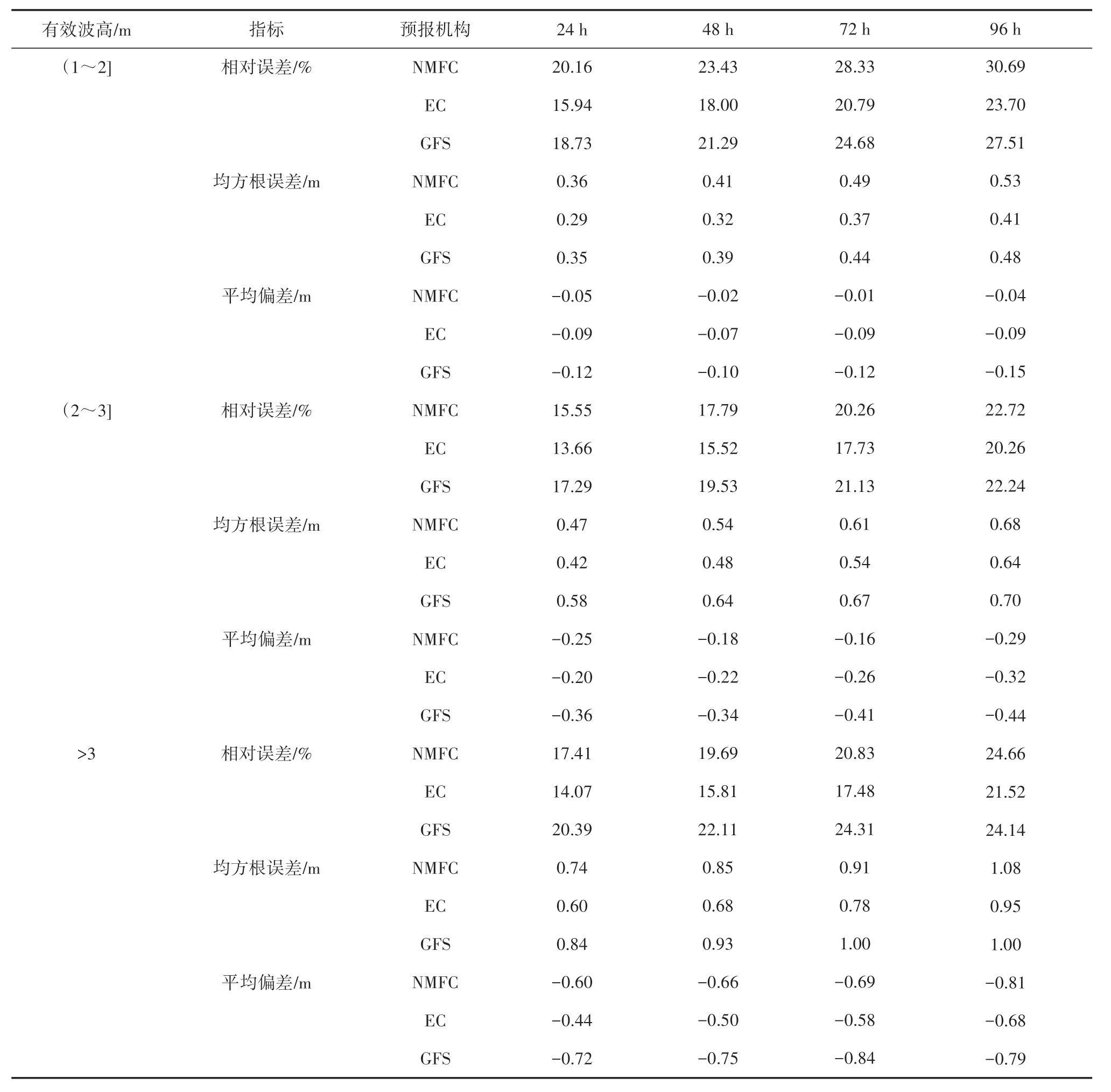
表2 有效波高预报误差统计Tab.2 Statistical parameter of the comparison of significant wave height forecasts with buoy observations

图2 为3 种产品的偏差箱线图，用来体现不同预报时效下预报偏差的离散程度和数据的集中趋势[23]。从图中可以看出，EC、NMFC 和GFS 24～96 h 有效波高的预报偏差中位数分别在0.06～0.08 m、0.04～0.09 m、0.01～0.02 m 之间，预报结果整体均略偏大。考虑到3 种产品对2 m 以上有效波高的预报偏差偏小，说明它们对2 m 以下有效波高的小浪预报偏大。从图中箱子和虚线长短来看，3种产品中EC 的离散程度最小，GFS 的负偏离较多，NMFC 的正偏离较多，说明EC 与观测更为接近，GFS 漏报较多而NMFC 误报较多。另外，从图中可以看出，3 种模式预报偏差的离散度随着预报时效的增长而不断增大。

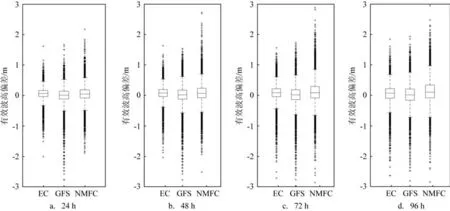
图2 不同模式24～96 h预报偏差箱线图Fig.2 Different model's box diagram of 24～96 h prediction

2.2 误差空间分布

根据10 m 大型海洋观测浮标所在的不同位置，将其划分为渤海、黄海北部、黄海中部3个海域分别进行误差统计分析，其中预报有效波高为0～2 m 的均方根误差结果见图3a，有效波高大于2 m 的均方根误差结果见图3b。从海区来看，当渤海区域的预报有效波高为0～2 m 时，EC 预报结果的均方根误差最小，NMFC 24 h 和48 h 预报结果次之，但72 h和96 h 预报结果的均方根误差大于GFS 预报。在有效波高为0～2 m 时，EC 24 h、48 h、72 h 和96 h 预报结果的均方根误差分别为0.33 m、0.37 m、0.38 m和0.44 m；而有效波高大于2 m时，EC 24 h、48 h、72 h预报结果的均方根误差分别为0.48 m、0.57 m、0.66 m，这3 项结果均为3 种产品中最优，96 h 预报结果的均方根误差为0.86 m，高于NMFC 的预报结果（0.83 m）。GFS 预报产品的均方根误差在有效波高大于2 m 时均为最大。在黄海北部，除有效波高大于2 m的96 h预报结果外，其余情况下EC预报结果的均方根误差均为最小，GFS次之，NMFC最大。在有效波高为0～2 m 时，EC 24 h、48 h、72 h 和96 h 预报结果的均方根误差分别为0.28 m、0.30 m、0.32 m和0.38 m;而有效波高大于2 m 时，EC 24 h、48 h、72 h 和96 h 预报结果的均方根误差分别为0.36 m、0.41 m、0.52 m 和0.61 m。在黄海中部，EC预报结果的均方根误差均为最小，GFS 预报误差多数情况下小于NMFC。

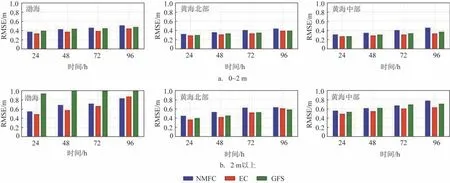
图3 不同海域有效波高预报均方根误差Fig.3 RMSE of significant wave height forecasts in different sea areas

从3 个海区的预报误差来看，EC 的预报效果在大多数情况下为最好，NMFC 和GFS 的预报结果在不同海区、不同预报时效以及不同有效波高范围下各有优劣。横向比较来看，3 种有效波高预报产品在渤海和黄海中部的误差大于黄海北部，其中GFS预报误差在渤海区域尤其大，可能是由于GFS 产品的参数化方案不适用于渤海这种短风区、浅水深海域，也可能与GFS 模式在渤海所用地形数据不准确有关，具体原因需要对GFS的模式设置进行分析。

考虑到海上浮标与海洋站的位置区别，将结果分为外海和近岸进行误差分析，结果见图4，其中近岸部分为所有海洋站结果，外海部分为所有海上浮标结果。从图中可以看出，3 种产品在近岸的误差均高于外海。对于2 m 以下有效波高的预报结果，3种产品在近岸的均方根误差比较接近，在外海EC的均方根误差最小；对于2 m 以上的有效波高，GFS在近岸的均方根误差严重偏大（超过1.3 m），EC 在外海的均方根误差最小，NMFC 在近岸的均方根误差最小，这可能与NMFC 的模式分辨率较高（1/36°）并采用了海图水深数据有关。

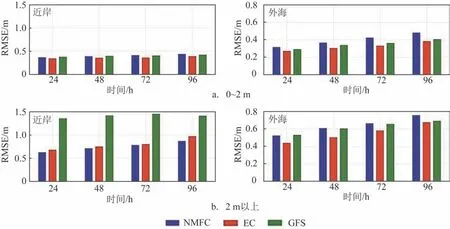
图4 近岸与外海有效波高预报均方根误差Fig.4 RMSE of significant wave height forecasts in the nearshore and open sea areas

泰勒图由TAYLOR[24]于2001 年首先提出，近年来被广泛应用于模式的评估与检验。基于余弦定理，泰勒图可巧妙将模式的相关系数、中心均方根误差和标准差之比3个评价指标整合在一张极坐标图上，图5 是3 种预报产品在所有观测站位的泰勒图，图中从圆点出发的径向距离表示模式与观测的标准差之比，比值越接近1，表示模拟能力越好；中心均方根误差是以观测点为圆心的半圆弧，模式点越靠近观测点，表明模拟越接近观测值；相关系数由方位角的余弦决定，当模式模拟结果与观测值较一致时，相对系数越接近1。从图中可以看出，在3种预报产品中，MF03007 浮标（位于黄海中部，最远离陆地）的误差均为最小，说明3种模式对该站的预报效果最好；从对近岸站位（尤其是小长山）的预报效果来看，NMFC 的预报效果好于其他两种模式，小长山站EC 和GFS 结果的标准差之比均大于1.0，中心均方根误差均大于0.8 m，相关系数均小于0.7；而GFS 对龙口站的预报效果十分不理想，中心均方根误差都大于1.0 m。从对海上浮标的预报效果来看，EC 整体好于其他两种模式，中心均方根误差相对较小，相关系数更接近1。

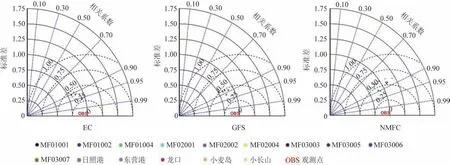
图5 EC、GFS和NMFC的48 h预报泰勒图Fig.5 Taylor diagram of 48 h prediction from the EC，GFS and NMFC products

2.3 误差时间分布

图6 为3 种产品48 h 有效波高预报误差的时间分布。从图中可以看出，3种产品在有效波高为0～2 m 时的均方根误差变化趋势较为一致且全年变化不大，冬季均方根误差略高于其他季节。当有效波高大于2 m时，3种产品的均方根误差显示出较大的差异，其中GFS 的预报结果在8 月和11 月误差偏大，经过统计发现是由于其对8 月的一次低压过程和11 月的3 次冷空气过程预报误差较大造成的，而NMFC 和EC 对这4 次过程的预报误差较小；EC 的预报结果在6 月误差偏大，这是因为EC 对6 月的一次低压过程有效波高预测偏小从而导致漏报。由此可以看出，对于渤海和黄海2 m 以上的有效波高来说，夏季海浪模式的预报水平主要取决于其对温带气旋、低压倒槽等低压过程有效波高的预报误差，而秋冬季则主要取决于对冷空气过程有效波高的预报误差。

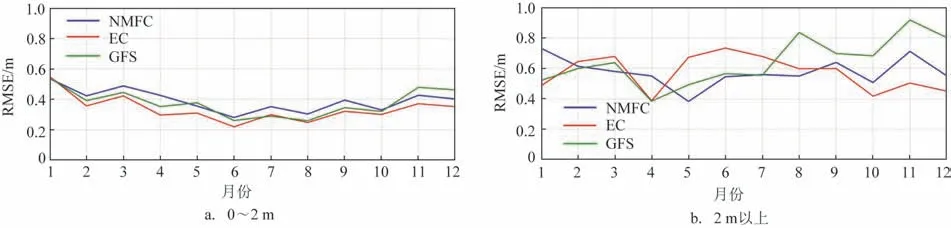
图6 各月份不同有效波高48 h预报均方根误差Fig.6 The monthly evolution of the RMSE of 48 h forecasts for different significant wave height

2.4 不同波向过程分析

挑选8 个海上浮标海浪观测数据，根据实测波向将其分成8 个方向，分别对3 种预报产品在不同波向时的预报进行误差分析，计算均方根误差并评估其在不同波向下的预报结果准确性，具体结果见表3。以24 h 结果为例，从表中可以看出EC 预报结果在8 个方向差别不大且均为最好；GFS 在E 向、S向效果较好，在W 向、NW 向效果略差；NMFC 在S向、SE向效果较好，在W向效果最差。

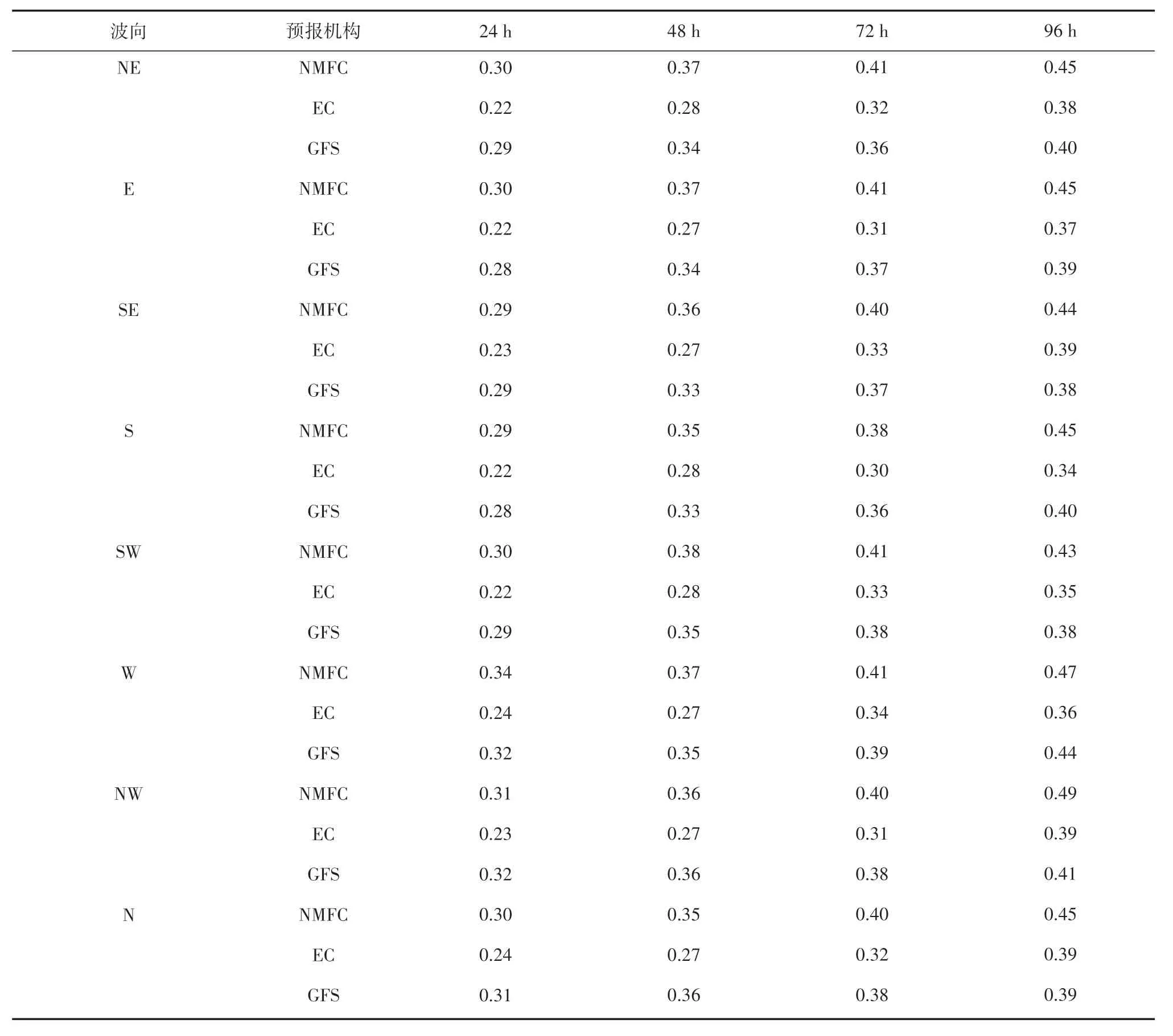
表3 不同波向有效波高预报均方根误差统计（单位：m）Tab.3 RMSE of significant wave height forecasts in different directions（unit：m）

2.5 强天气过程分析

根据海浪观测数据挑选2 m 有效波高以上的天气过程时间窗口，并按照冷空气、温带气旋、台风、低压倒槽、东高西低（即东面为副热带高压带，西面为大低压带）5 类天气过程进行分类，依照分类分别对不同天气过程的预报误差进行评估。分类结果显示，2021 年渤海和黄海大浪过程主要由冷空气（26次）和温带气旋（10次）两种天气过程导致，台风（3 次）、低压倒槽（3 次）和东高西低（1 次）的天气过程发生频率较低。由于东高西低过程只出现了1次，缺乏代表性，故本次分析不考虑东高西低过程。

将4种不同天气过程下的数值预报结果与浮标实测结果进行对比并分析2 m 以上有效波高的预报均方根误差，结果见图7。通过分析可以得出，冷空气期间，EC 的预报误差（均方根误差为40～80 cm）最小，GFS 的预报误差最大，NMFC 的预报误差居中，NMFC 的96 h 预报误差比EC 的略小；温带气旋期间，3 种数值预报结果的总体误差水平接近，NMFC 在24～72 h 的预报误差较小，但96 h 的预报误差偏大；低压倒槽期间，NMFC 的预报误差小于EC 和GFS；台风及台风外围影响期间，NMFC 的24 h 预报误差最小，而EC 的48～96 h 预报误差最小。由于2021 年影响渤海和黄海的低压倒槽和台风过程均仅有3 次，所以该结果的可参考性仍需进一步研究。总体来说在3 种产品中，EC 对于冷空气作用期间海浪的预报效果较好，NMFC 对于温带气旋等低压过程期间海浪的预报效果较好。

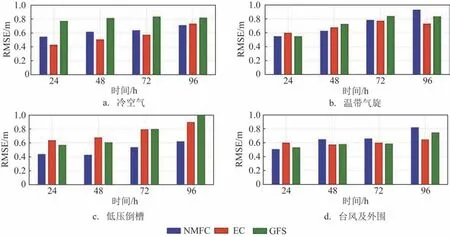
图7 不同天气过程有效波高预报均方根误差Fig.7 RMSE of significant wave height forecasts in different weather situation

图8 是在2021 年10 月3—5 日冷空气过程中渤海中部浮标有效波高随时间的变化曲线。从图中可以看出，3 种产品的有效波高预报峰值比较接近，但都小于观测值。在有效波高下降的过程中，EC的预报结果和实测更接近，所以EC 的预报误差最小。EC对于此次冷空气过程的预报波高衰减更慢，可能是由于其海浪数值模式中的能量耗散参数化方案更有利于冷空气期间海浪能量的长距离传播。

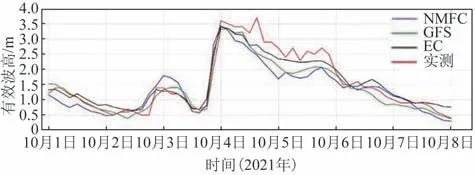
图8 一次冷空气过程有效波高随时间变化曲线图Fig.8 Comparison of significant wave height forecasts with observations for the waves during a typical cold air activity

图9 为在2021 年6 月14—16 日低压倒槽过程期间黄海中部浮标有效波高随时间的变化曲线。从图中可以看到，EC 与GFS 对此次低压倒槽过程的有效波高极值的预报水平相当，但与实测相比均偏小，预报值与实测极值相差约1 m，而NMFC虽然对于极值出现时间的预报比其他二者略有提前，但预报结果与实测极值最接近，仅相差不足0.5 m，这可能与NMFC所使用的风场驱动较为准确有关。

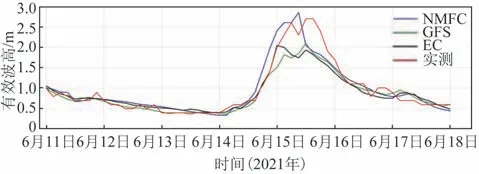
图9 一次低压倒槽过程有效波高随时间变化曲线图Fig.9 Comparison of significant wave height forecasts with observations for the waves during a typical inverted trough activity

我们使用逐3 h预报数据，针对4种过程下预报与实测波高极值的出现时刻进行分析，得出相应相位差。定义在某次过程中某个浮标/台站实测波高极值出现在预报时间之前为预报滞后，反之为预报提前。筛选4种天气过程下具有代表性的实测数据进行统计，具体结果见表4。在冷空气发生时，3 种预报产品预报滞后出现次数明显高于预报提前，NMFC 产品平均滞后时间约为5.58 h，EC 和GFS 产品为5.61 h 和5.55 h；而当预报提前时，NMFC 产品平均提前时间为5.19 h，EC 产品为5.31 h，GFS 产品为5.19 h。温带气旋下3 种预报产品预报滞后出现次数略高于预报提前，NMFC 产品平均滞后时间约为5.61 h，EC 和GFS 产品为5.94 h 和6.03 h；而当预报提前时，NMFC 产品平均提前时间为6.36 h，EC产品为6.33 h，GFS 产品为6.14 h。台风和低压倒槽过程发生次数相对较少，此处不做分析。

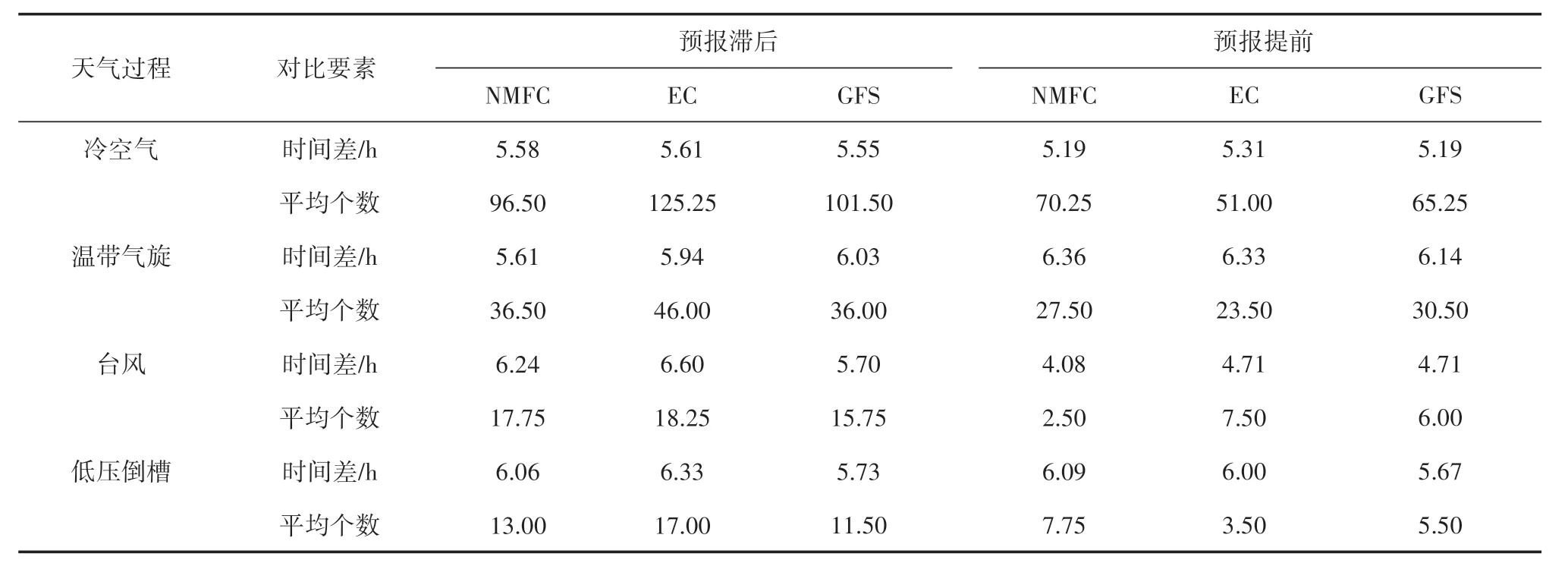
表4 有效波高预报极值结果与实测结果出现时间差Tab.4 Occurring time difference between the forecasted significant wave height extreme and the observed extreme

2.6 极值预报误差分析

考虑到预报机构对外发布的海洋预报结果通常以天为单位，本文对日极值预报结果进行误差分析。采用NMFC的逐时预报数据、EC和GFS的逐3 h预报数据统计每日预报的最大有效波高且结果大于2 m 的时刻，并与利用逐时观测数据统计得到的每日观测最大有效波高进行对比，结果见图10。从图中可以看出，对于有效波高极值NMFC 的预报最好，EC 的效果略差（96 h 预报误差变大），GFS 的预报误差最大。结合表3可知，尽管EC有效波高的总体误差低于NMFC，但在极值预报方面却不如NMFC。这是因为NMFC为逐时预报产品，而EC和GFS 为逐3 h 产品，在捕捉极值方面逐时预报产品更有优势。

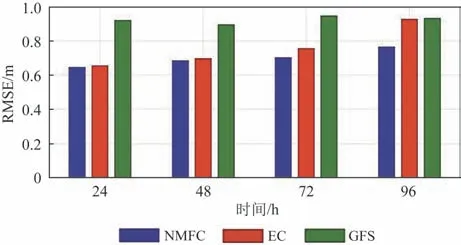
图10 2 m以上有效波高日预报误差统计Fig.10 RMSE of daily significant wave height(>2 m)forecasts

3 总结与讨论

本文收集整理了2021 年NMFC、EC、GFS 的海浪数值预报产品以及渤海和黄海浮标和海洋站的海浪观测数据，将模式数据和观测数据进行比较并统计分析了多种误差指标。总体来说，3种数值预报产品对2 m 以上有效波高24 h的预报误差不超过19%，EC 预报误差最低，3 种产品对于大浪过程的预报结果都偏低。从空间上看，渤海和黄海中部的有效波高预报误差大于黄海北部（其中GFS在渤海的误差尤其大）；近岸的有效波高预报误差均高于外海；EC 有效波高预报误差在外海最小，NMFC 误差在近岸最小。从月份来看，GFS 的有效波高在8 月和11 月误差偏大，EC 有效波高误差在6月偏大，NMFC 有效波高预报误差全年变化不大，总体来说夏季预报误差偏大。在天气过程方面，EC对冷空气和台风期间海浪的预报效果更好，NMFC对温带气旋和低压倒槽期间海浪的预报效果更好。在极值预报方面，NMFC 对有效波高极值的预报最好，EC的效果略差，GFS的预报误差最大。

本文仅对2021 年3 种预报产品的预报性能进行了初步研究，今后应针对多年的预报产品开展更加系统的评估，以期为日后进行的实际有效波高的预报订正和释用提供有意义的参考。另外，在渤海和黄海，海浪的预报水平既取决于海浪模式的参数设置，还取决于海面风的预报水平，抛开海面风误差只分析海浪误差，不能完全确定海浪误差的全部来源。因此，下一步应将海面风预报效果和海浪预报效果进行关联分析，明确海浪预报误差中的模式自身误差和强迫场误差的贡献。