风载下塔式起重机在建筑物环境的安装位置研究*

王 毅

南京铁道职业技术学院 南京 210031

0 引言

塔式起重机（以下简称塔机）是建筑施工中的一种主要水平和垂直运输机械，其工作环境在室外，受自然风荷载的影响较大。钝体建筑物会改变主要风向的流向，是低速不可压缩的流，其周围流场复杂，有撞击、分离、再附、环绕和涡旋等状态。塔机安装在建筑物附近，通过附墙装置与建筑物连接在一起，其所在的风场受建筑物影响，故研究建筑物环境下塔机的安装位置对提高塔机的抗风能力具有重要意义[1]。

本文采用CFD 计算流体力学，在Ansys CFX 中建立塔机风场模型，研究在风载建筑物环境下不同水平和垂直方向的安装位置对塔机的影响。

1 粘性流动的基本方程

粘性是流体的一种物理特性，反映了流体抵抗剪切变形的能力。由牛顿流体的内摩擦定律可知，粘性应力与粘度系数及速度梯度的关系为[2]

式中：μ为粘度系数。

塔机的工作环境处在大气边界层中，气流在大气边界层中的流动属于湍流，为低速不可压缩的粘性牛顿流体。任何流体的流动都遵循质量守恒定律、动量守恒定律和能量守恒定律。

1.1 质量守恒方程

质量守恒方程的定义是单位时间内流体微元体中质量的增加量等于同一时间间隔内流入该微元体的净质量，根据这一定律可得出其表达式为

式中：ρ为密度，t为时间，μ、v、w分别为速度矢量在x、y、z方向上的矢量。

1.2 动量守恒方程

动量守恒方程通常被称为运动方程，该定律可表达为：在单位时间内微元体内流体动量变化率等于作用在微元体的所有外力的和[50]。动量方程的表达式为

式中：ρ为流体微元体的压力，τxx、τxy、τyz分别为分子粘性作用产生的微元体表面粘性力的分量，Fx、Fy、Fz分别为微元体上的体力。

1.3 能量守恒方程

能量守恒定律描述为：控制微元体上能量的增加率为体力、面力对其所做的功与进入其内部的净热流量的总和[3]。该定律的方程表达式为

式中：Cp为流体比热容；T为温度；k为流体传热系数；ST为流体粘性耗散项，主要指流体在运动时由黏性作用机械能转化为内能的部分。

能量守恒方程虽为塔机风场求解的基本控制方程之一，但本文所用流体为不可压缩气体，热交换量较小可忽略不计，所以数值模拟计算时只需联立动量方程和质量方程，无需考虑能量方程。

2 构建模型

为精确模拟塔机在真实风场中的风载分布情况，按1:1 比例在Pro E 中建立简易QTZ5010 塔机的几何模型，该模型省去了驾驶室、拉杆、法兰、螺栓和回转支撑系统等部件，塔机简易模型如图1 所示。塔机高度为35 m，标准节为1.4 m×1.4 m×2.4 m，标准节主肢选用□135×10 的方钢，标准节斜腹杆采用□60×4 方钢，起重臂长为28 m，上弦杆采用Φ80×8 的圆管，下弦杆采用□100×10 的方钢，起重臂斜腹杆采用Φ60×4 的圆管。

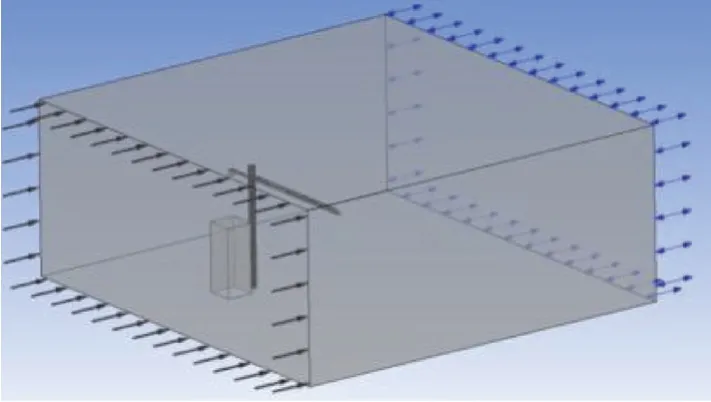
图2 计算模型图

风场计算域设置为125 m×120 m×50 m。将塔机Pro E 模型保存为.iges 格式，将几何模型导入Workbench 软件设计模块（DM），并构建风场环境，建筑物[4]尺寸为8 m×8 m×20 m，将塔机放在计算域风流动方向三分之一处，计算模型图如2 所示。网格采用ICEM CFD自动划分网格，网格质量达到0.02 m以上，网格节点总数为3 668 152，网格单元总数量21 813 652，网格如图3 所示。在计算域模型中，流体质量密度（空气）取值为1.29 kg/m3，粘度系数取1.79×10-5kg/（m·s）。

图3 计算模型网格图

3 塔机与单个建筑物水平位置关系

建立图4 所示塔机在有建筑物环境下的风场模型。模拟塔机的A、B、C 等位置，其中A 处为正对建筑物中间位置，B 处偏离A 处2 m，C 处偏离B 处2 m，分别受到Wind +X（0°风向角）、Wind +Y（90°风向角）、Wind-X（180°风向角）、Wind-Y（270°风向角）等4 种风向风时风压分布、风速、风向、涡流分布和塔机根部倾覆力矩的情况[5]。

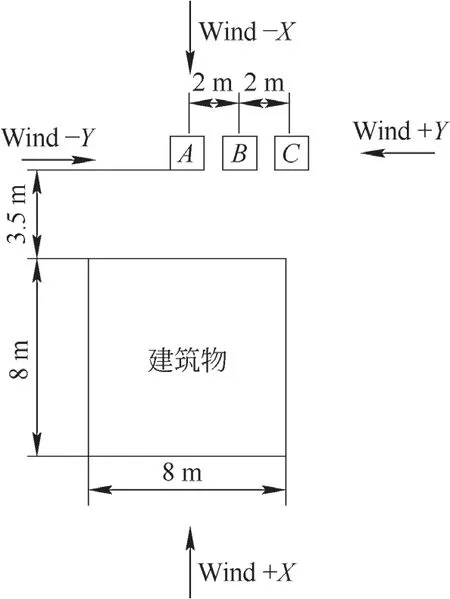
图4 安装位置示意图

3.1 Wind+X 风向（0°风向角）

采用CFX 模拟塔机位于A、B、C 等位置受Wind+X风向风时的风场规律。表1 为塔机在各安装位置的风环境规律统计表，图5 所示为10 m 高度处的流场风速云图。

表1 塔机在各安装位置的风环境规律

图5 流场10 m 高度处的风速云图

由图5 可知，通过观察速度云图的颜色可以初步了解流体在不同位置的速度和，从而判断流场的特征。A 位置的最大风速为72.45 m/s，B 位置的最大风速为72.56 m/s，C 位置的最大风速为73.33 m/s；由此表明最大风速VAmax＜VBmax＜VCmax，即在A 位置的最大风速最小，B 位置次之，C 位置最大。

由表1 可知，塔机受Wind +X风向风时，其根部的倾覆力矩表现为MA＜MB＜MC，即在A 位置的倾覆力矩最小，B 位置次之，C 位置最大。最大压力差C 位置最小，其次是A 位置，B 位置最大。因此，在受Wind+X风向风时，塔机相对于建筑物，安装在A 位置最合适。

3.2 Wind+Y 风向（90°风向角）

采用CFX 模拟塔机位于A、B、C 等位置受Wind+Y风向风时的风场规律。表2 为塔机在各安装位置的风环境规律统计表，图6 为流场中心面压强云图。

表2 塔机在各安装位置的风环境规律

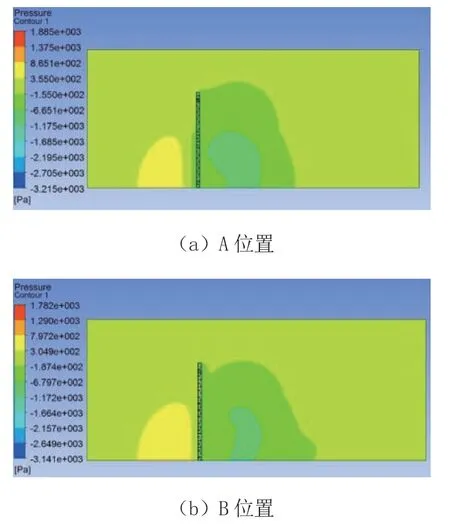
图6 流场中心面压强云图

由图6 可知，不同颜色代表压强大小值不同，红色代表压强值很大，A 位置最大风压为1.885×103Pa，最小风压为-3.215×103Pa；B 位置最大风压为1.782×103Pa，最小风压为-3.141×103 Pa；C 位置最大风压为1.825×103Pa，最小风压为-3.013×103Pa，即PBmax＜PCmax＜PAmax，表明最大压力差在C 位置最小，其次是B 位置，A 位置最大。

由表2 可知，塔机受Wind +Y风向风时，塔机根部的倾覆力矩MC＜MB＜MA，即在C 位置最小，B 位置次之，A 位置最大；由此表明最大风速VCmax＜VBmax＜VAmax，即在C 位置最小，B 位置次之，A 位置最大。因此，在受Wind +Y风向风时，A 位置弱于B、C 位置，但考虑到Wind +Y风向（90°风向角）与Wind-Y风向（270°风向角）的关联性，需综合分析。

3.3 Wind-X 风向（180°风向角）

采用CFX 模拟塔机位于A、B、C 位置受Wind-X风向风时的风场规律。图7 为流场中心面风速流线图，表3 为塔机在各安装位置的风环境规律统计表。

表3 塔机在各安装位置的风环境规律

图7 流场中心面风速流线图

图7 反映了空气中气流的真实运动情况，A 位置的最大风速为67.11 m/s，B 位置的最大风速为66.77 m/s，C 位置的最大风速为67.82 m/s；由此表明最大风速VBmax＜VAmax＜VCmax，即在B 位置最小，A 位置次之，C 位置最大。

由表3 可知，在塔机受Wind-X风向风时，塔机根部的倾覆力矩为MA＜MB＜MC，即在A 位置最小，B位置次之，C 位置最大。由此表明最大压力差B 位置的最小，其次是C 位置，A 位置最大，但差别不大。因此，在受Wind-X风向风时，C位置最差，A、B位置各有优势。

3.4 Wind-Y 风向（270°风向角）

采用CFX 模拟塔机位于A、B、C 等位置受Wind-Y风向风时的风场规律。表4 为塔机在各安装位置的风环境规律统计表，图8 为流场中心面速度云图。

表4 塔机在各安装位置的风环境规律

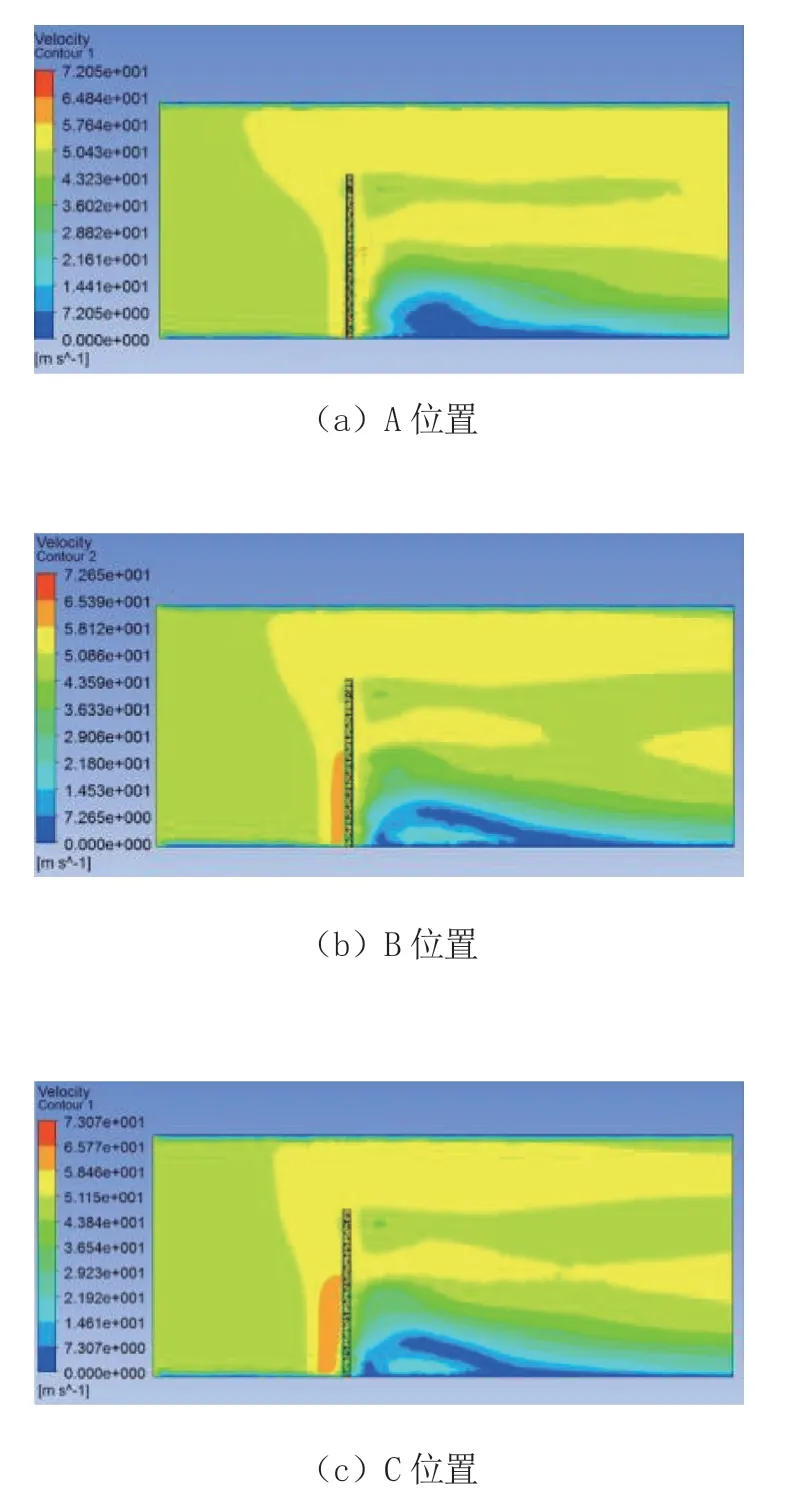
图8 流场中心面速度云图

由图8 可知，A 位置的最大风速为72.05 m/s，B 位置的最大风速为72.65 m/s，C 位置的最大风速为73.07 m/s；由此表明最大风速VBmax＜VAmax＜VCmax，即在A位置最小，B 位置次之，C 位置最大。

由表4 可知，塔机受Wind -Y风向风时，塔机根部的倾覆力矩MA＜MB＜MC，即在A 位置最小，B 位置次之，C 位置最大。由此表明最大压力差A 位置的最小，其次是C 位置，B 位置最大。因此，在受Wind-Y风向风时，相对于建筑物塔机安装在A 位置最合适。

综上所述，当塔机安装在相对于建筑物的A、B、C 等位置时，分别受到Wind +X（0°风向角）、Wind+Y（90°风向角）、Wind-X（180°风向角）、Wind-Y（270°风向角）风向风，对比表1 ～表4 和图9 中的数值，Wind +X、Wind-X和Wind-Y风向时塔机在A位置的根部倾覆力矩最小。虽然在Wind +Y风向时塔机在C 位置根部倾覆力矩最小，但在Wind-Y风向时塔机在C 位置根部倾覆力矩最大。如表5 所示，塔机在A 位置受4 个风向角风作用下平均倾覆力矩为1.459 9×106N·m，B 位置受4 个风向角风作用下平均倾覆力矩为1.502 8×106N·m，C 位置受4 个风向角风作用下平均倾覆力矩为1.512 5×106N·m，由此可知A 位置是最适合安装塔机的位置。从水平位置考虑，在风载作用下，方形建筑物一侧的中间位置最适合安装塔机。

表5 塔机在各安装位置的平均倾覆力矩 N·m

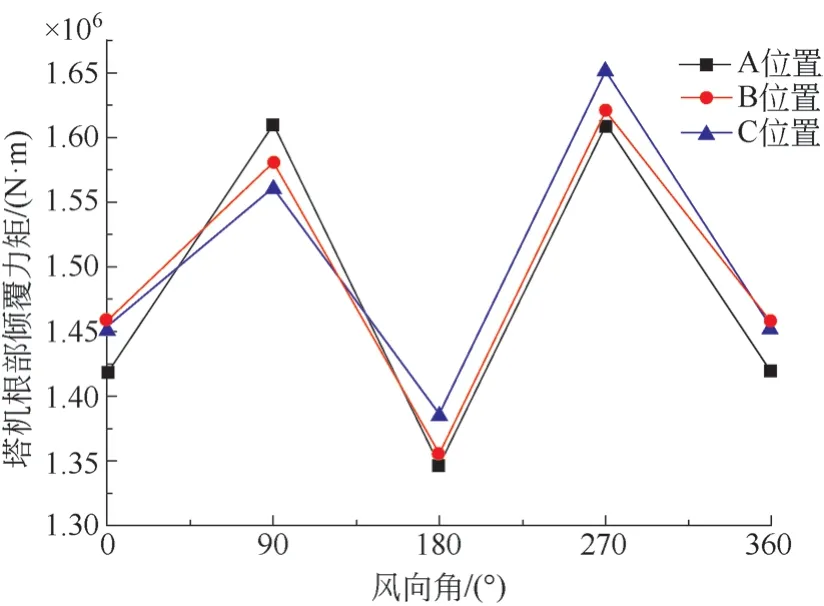
图9 A、B、C 等位置塔机根部倾覆力矩图

4 塔机与单个建筑物垂直位置关系

如图10 所示，建立塔机与建筑物垂直位置的风场模型[6]，模拟塔机分别安装在D、E、F、G、H 等位置受到Wind +X、Wind +Y、Wind-X、Wind-Y风向时的风场情况，其中D 位置距离建筑物3.5 m，E 位置距离建筑物4 m，F 位置距离建筑物4.5 m，G 位置距离建筑物5 m，H 位置距离建筑物5.5 m。

图10 塔机安装位置示意图

4.1 Wind+X 风向（0°风向角）

采用CFX 模拟塔机位于D、E、F、G、H 等位置受Wind +X风向风时的风场规律。图11 为10 m 高度处流场风速云图，表6 塔机在各安装位置的风环境规律统计表。

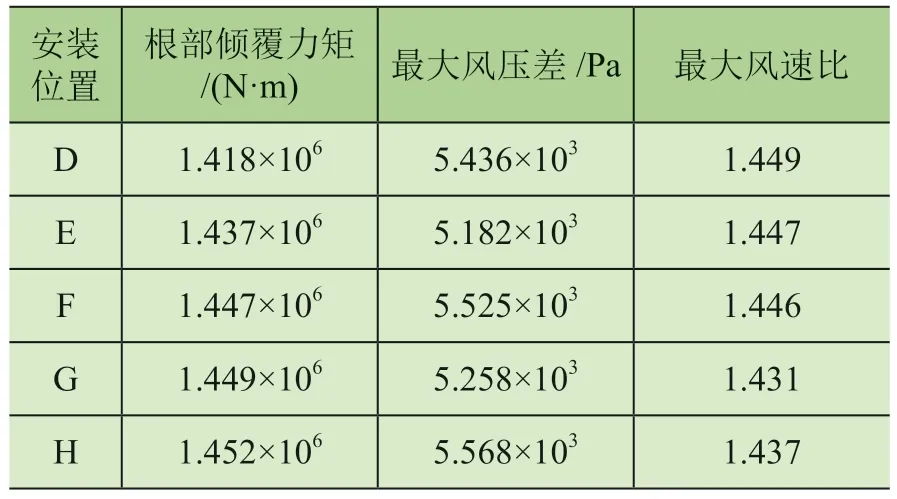
表6 塔机在各安装位置的风环境规律

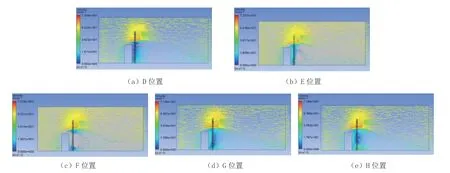
图11 流场中心面速度矢量图

由图11 可以看出等速和风的方向，D 位置的最大风速为72.45 m/s，E 位置的最大风速为72.35 m/s，F 位置的最大风速为72.28 m/s，G 位置的最大风速为71.56 m/s，H 位置的最大风速为71.86 m/s；由此表明最大风速VGmax＜VHmax＜VFmax＜VEmax＜VDmax。

由表6 可知，塔机受Wind +X风向风时，塔机根部的倾覆力矩MD＜ME＜MF＜MG＜MH。

4.2 Wind+Y 风向（90°风向角）

采用CFX 模拟塔机位于D、E、F、G、H 等位置受Wind +Y风向风时的风场规律。图12 为流场10 m 高度处的风速云图，表7 塔机在各安装位置的风环境规律统计表。

表7 塔机在各安装位置的风环境规律

图12 流场10 m 高度处的风速云图

由图12 可知，D 位置的最大风速为72.05 m/s，E位置的最大风速为70.91 m/s，F 位置的最大风速为70.5 m/s，G 位置的最大风速为70.7 m/s，H 位置的最大风速为70.62 m/s；由此表明最大风速VFmax＜VHmax＜VGmax＜VEmax＜VDmax，即在F 位置最小，H 位置处次之，两者相差0.12 m/s。

由表7 可知，塔机受Wind +Y风向风时，塔机根部的倾覆力矩MH＜MG＜MF＜ME＜MD，即在H 位置时最小。因此，在受Wind +Y风向风时，相对于建筑物塔机安装在H 位置最合适。

4.3 Wind-X 风向（180°风向角）

采用CFX 模拟塔机位于D、E、F、G、H 等位置受Wind-X风向风时的风场规律。图13 为流场中心面风压云图，表8 塔机在各安装位置的风环境规律统计表。

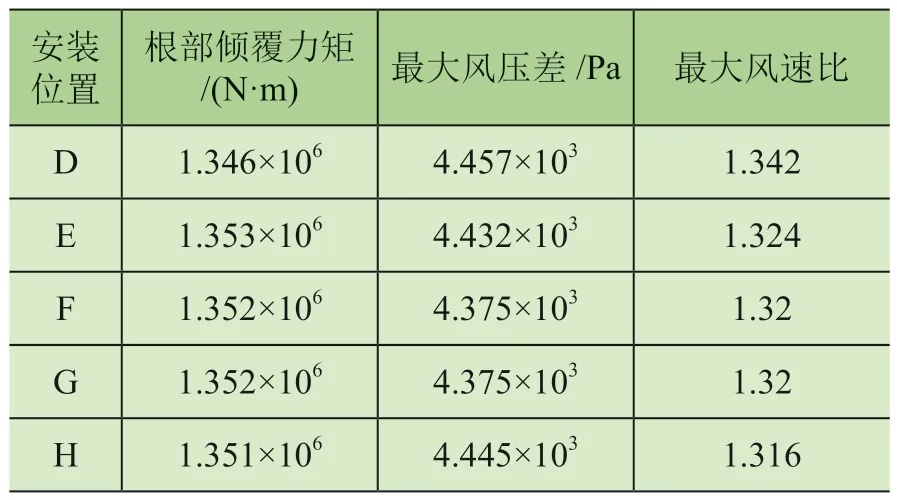
表8 机在各安装位置的风环境规律

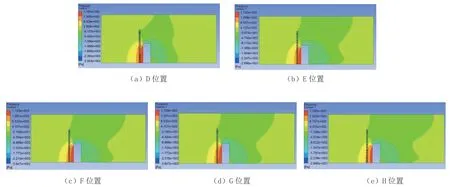
图13 流场中心面压强云图

由图13 可知，D 位置的最大风压为1.767×103Pa，E 位置的最大风压为1.742×103Pa，F 位置的最大风压为1.728×103Pa，G 位置的最大风压为1.728×103Pa，H 位置的最大风压为1.765×103Pa；由此表明最大风压PFmax＜PGmax＜PEmax＜PHmax＜PDmax。

由表8 可知，塔机受Wind-X风向风时，塔机根部的倾覆力矩MD＜MH＜MG＜MF＜ME，D 位置处最小，H 位置次之。

4.4 Wind -Y 风向（270°风向角）

塔机在D、E、F、G、H 等位置受到Wind-Y风向风的情况与受到Wind +Y风向风的工况一致，故不再重复研究。综上所述，当塔机安装在相对于建筑物的D、E、F、G、H 等位置时，分别受到Wind +X（0°风向角）、Wind +Y（90°风向角）、Wind-X（180°风向角）、Wind-Y（270°风向角）风向风，对比表6 ～表8 中的数值，可得出塔机在各安装位置的平均倾覆力矩。

如表9 和图14 所示，塔机在D 位置受4 个风向角风作用的平均倾覆力矩为1.459 9×106N·m，E 位置的平均倾覆力矩为1.494 25×106N·m，F 位置的平均倾覆力矩为1.490 75×106N·m，G 位置的平均倾覆力矩为1.488 25×106N·m，H 位置的平均倾覆力矩为1.486 25×106N·m；由此可知，塔机各风向根部倾覆力矩方差也逐渐变小，H 位置最小，故H 位置是最适合安装塔机的地址。

表9 塔机在各安装位置的平均倾覆力矩

图14 D、E、F、G、H 等位置塔机根部平均倾覆力矩图

5 结论

1）根据塔机处于建筑物的A、B、C 等位置时受到Wind+X、Wind-X、Wind+Y、Wind-Y等风向的模拟结果，得出塔机安装在A 位置最安全，即从水平位置考虑，在风载作用下，方形建筑物一侧的中间位置是塔机最优安装位置。

2）根据塔机处于建筑物的D、E、F、G、H 等位置时受到Wind+X、Wind-X、Wind+Y、Wind-Y等风向的模拟结果，得出塔机安装在H 位置最安全，即从竖直位置考虑，在合理距离范围内，塔机的安装位置离方形建筑物越远越安全。