基于正交投影的子带信息几何雷达弱小目标检测方法

杨 政 程永强 吴 昊 黎 湘 王宏强

(国防科技大学电子科学学院 长沙 410073)

1 引言

复杂背景下的弱小目标检测一直是雷达目标检测领域的难点问题，其检测性能主要受到杂波和干扰等因素的影响。特别是在实际环境中，存在杂波和干扰，且杂波强度大，常常呈现非均匀、非平稳等特性。同时，如海面小型渔船、小型船艇和漂浮物等弱小目标的雷达截面积小，回波微弱，信杂比低，极易淹没在强杂波中，这导致目标与杂波在时域、频域均难以区分，给目标检测带来了巨大挑战[1-4]。目前，现有经典的检测方法有基于单元平均恒虚警率检测(Cell Averaging Constant False Alarm Rate,CA-CFAR)，其主要通过待检测单元周围邻近的参考单元估计杂波功率，以设置检测阈值，但强杂波背景会导致检测阈值过高，进而影响检测性能[5]。之后，通过相参积累提升信杂比的方法被广泛研究，典型的如基于快速傅里叶变换(Fast Fourier Transform,FFT)进行相参积累的CFAR检测方法[6]，然而，其检测性能依赖于较多的脉冲个数。实际中，由于雷达短暂的驻留时间和信号高效处理的需求，常常面临脉冲数较少的情形，此时，多普勒滤波器组的能量泄露以及杂波谱的展宽对该检测方法的性能影响严重。为避免这些缺点，自适应的相参积累检测方法得到大量研究，经典的如文献[7]提出了归一化匹配滤波检测方法(Adaptive Normalized Matched Filter,ANMF)，依靠杂波协方差矩阵对雷达回波进行白化滤波，并获得较好性能。随后，针对各种目标检测环境，一系列自适应类的匹配滤波检测方法被提出[8-11]。但是在实际复杂环境中，自适应类的匹配滤波检测方法面临如下问题：(1)协方差矩阵估计精度对性能影响较大，如杂波的非均匀性导致用于估计的均匀杂波样本数较少，估计误差较大，以及干扰信号的存在也将影响协方差矩阵估计的稳健性；(2)实际检测中目标多普勒未知，回波信号与模型之间容易出现多普勒失配，进而影响检测性能；(3)雷达回波在相参处理间隔(Coherent Process Interval,CPI)内的非平稳性也极大地限制着该类检测器的性能。为此，有相关学者设计了子带滤波器，并结合ANMF方法，提出了子带归一化自适应匹配滤波器(Subband Adaptive Normalized Matched Filter,SANMF)[11,12]，通过子带滤波抑制带外杂波，保留带内信号并改善其短时平稳性，并取得较好效果。此外，研究人员也常考虑如基于奇异值分解、时频滤波和子空间等的杂波抑制方法，以改善目标检测性能[13-15]。

作为新兴的雷达目标检测技术，矩阵信息几何(Matrix Information Geometry,MIG)检测方法近年来逐渐发展并得到诸多研究。在国内，国防科技大学对于基于信息几何的雷达目标检测方法做了大量研究，取得了较多研究成果[16-20]。研究表明：该方法无需杂波先验信息，且针对复杂背景下的目标检测，特别是均匀样本数少和脉冲数少的情形，具有一定的性能优势。在国外，法国学者将信息几何理论应用在雷达目标检测领域，提出了一种矩阵CFAR检测器，并验证了该检测器相对于传统基于FFT相参积累的CFAR检测方法的优越性[21,22]。区别于传统FFT相参积累的CFAR检测方法和自适应匹配滤波类检测器，MIG检测器将雷达回波数据统计建模为协方差矩阵，并利用协方差矩阵构成的矩阵流形，从而将目标检测问题转化为流形上目标与杂波的区分问题。由于目标与杂波统计特性的不同，二者在流形空间的区域分布也不同，从而可以利用流形空间的几何距离，区分目标与杂波，最终实现目标检测。MIG检测器首先是在矩阵流形上定义黎曼距离(Riemannian Distance,RD)作为目标与杂波的差异性度量，并有学者将其应用到飞机尾流目标检测[23]。随后，为解决黎曼距离计算复杂度较高的问题，一些计算量较低的散度度量得到诸多研究，并拓展了现有的几何距离度量方式[17,24]。为提升复杂杂波背景下的目标检测性能，研究人员从流形的几何结构出发，相继提出了一些基于流形度量和优化的检测方法[25-28]。

研究表明，MIG检测器具有良好性能的关键在于提取雷达回波中目标与杂波的差异性特征，并在高维特征流形空间进行有效区分。然而，在实际复杂背景下，弱小目标极易淹没在非均匀、非平稳的强杂波中，导致目标与杂波难以区分，进而限制着MIG检测器的性能。对于以上检测背景，本文采用子带滤波以减弱带外强杂波影响，但是由于子带内的强杂波信号依旧存在，需进一步考虑子带内的强杂波抑制。因此，受启发于子空间思想[29-31]，本文在矩阵流形上估计子带内杂波信号子空间，提出基于流形的正交投影方法，抑制强杂波信号，最终实现稳健有效的几何检测。最后，采用仿真数据与实测海杂波数据验证所提方法的检测性能。

下文中a,a,A分别表示标量、向量和矩阵，(·)T和(·)H分布表示转置和共轭转置操作，(·)∗表示取共轭，E表示数学期望，Cn表示n维复向量的集合，Cn×n表 示n×n维 复矩阵的集合，G L(·)表示线性群，0和I分别表示零矩阵和单位矩阵，t r(·)表示矩阵的迹，‖·‖F表 示矩阵Frobenius范数，log(·)表示矩阵对数，|·| 表示矩阵行列式，[K]表示取值1,2,...,K，{Ak}k∈[K]表示矩阵集合{A1,A2,...,Ak,...,AK}，{ak}k∈[K]表 示向量集合{a1,a2,...,ak,...,aK},d (·)表示求导符号，inf 表示下确界，j为虚数单位。

结果提示，新型关注型心理护理应用于骨折手术患者能够通过对心理干预的实施帮助患者获得更加积极的正面的心理状态，能够更好的正视疾病，并树立并配合掌握良好的态度，提高了下肢运动功能及日常生活能力，也提高睡眠质量和患者护理满意度，改善预后。

2 问题描述与信息几何检测

2.1 问题描述

对于脉冲多普勒雷达，假设雷达接收的待检测单元回波为z，一般地，雷达目标检测的问题可以表示为二元假设检验模型：

其中，z=(z1,z2,...,zn)T为N维脉冲数据，z∈Cn，K表示参考单元数。在H0假设下，待检测单元只含杂波c和噪声n，ck表示参考单元杂波；在H1假设下，待检测单元不仅包含杂波c和噪声n，还有目标信号s，且目标信号与杂波、噪声是统计独立的。其中，目标信号可以表示为s=ϖp，ϖ表示目标的幅度参数，p为多普勒导向矢量，即

让学生在自主学习的过程中学会和同学相互合作、学会分析问题，让所有学生都可以快乐的学习。但根据现阶段的学习模式而言，知识主要是靠教师和书本来传播的，效率低、方法单一，不利于学生的自主学习。将现代信息技术带到课堂，可以扩大学生的学习空间，使他们能高效快速地掌握更多的知识。例如，当教师在讲解“地球表面”一课时，教师可以带学生去机房，通过图片、视频等方式能使学生主动去接受这些知识，从而提高教学质量。

其中，fd为目标多普勒频率，Tr为脉冲重复间隔，n表示一个相参处理时间内的脉冲数。

2.2 矩阵流形及几何检测

由于雷达目标检测问题可以视为目标与杂波的区分问题，因此如何较好地提取目标与杂波的差异性信息，是对二者进行有效区分的关键。这里，考虑提取目标与杂波的时域相关性信息，而协方差矩阵正好能够较好地表征雷达回波脉冲数据间的相关性，即数据的2阶统计特性。因此，对于接收的雷达回波信号z，可以构建协方差矩阵

假设信号z满足广义平稳性质，则相关系数rκ可以由时间平均替代统计期望进行估计[21]，即

(1) 特普利茨结构[32]；

推论3当协方差矩阵集合{R1,R2,...,RK,C1,C2,...,CP}的均值为LE均值时，其影响函数为

(2) 埃尔米特对称性：R=RH；

MSTAR数据集是通过高分辨率的聚束式合成孔径雷达采集到的静止车辆的SAR切片图像，包括多类目标SAR图像数据。实验中，训练样本为17°方位角的SAR图像数据，测试样本为15°方位角的SAR图像数据。在10类目标识别实验中，实验数据包括BMP2，BTR70，T72，2S1，BRDM2，ZSU234，BTR60，D7，T62，ZIL131十类目标数据。采用数据增强对训练样本进行扩充，通过像素平移的方法使得每类训练数据在原有基础上扩充了5倍，10类目标测试与训练数据分布如表2所示。

其中，B表示利用回波信号的相关性特征构建HPD矩阵。信息几何是在矩阵流形上采用微分几何方法研究矩阵数据的信息处理问题。通过定义的黎曼度量，构成了具有非正曲率的黎曼流形，它是一个可微的拓扑空间，具有凸锥结构且局部近似为欧氏空间[33-36]，也称为矩阵流形M。基于矩阵信息几何理论，雷达目标检测的问题可以转化为矩阵流形上几何问题。具体地，对接收的距离-脉冲回波信号，通过相关性特征映射，几何检测可视作流形上待检测单元和参考单元的区分问题，检测决策为待检测单元RD与 参考单元几何中心RG的几何距离与门限η进行比较，即

矩阵信息几何检测器原理框如图1所示，相比于传统CFAR检测方法直接采用回波数据的算术平均(1阶统计量)估计背景杂波，几何检测器利用流形的几何均值(2阶统计量)估计杂波，并在非均匀强杂波背景下，具有更好的稳健性[17,19]。

图1 矩阵信息几何检测器原理框图Fig.1 Block scheme of MIG detector

2.3 几何距离度量

通常，线性相位的DFT调制滤波器可以由一个有限冲激响应的低通原型滤波器产生，其频率响应为

对于矩阵流形上的两点R1,R2∈M，其几何解释如图2所示，区别于欧氏直线(黄色)，两点是由沿着流形曲面的曲线连接(红色)，其中最短路径的曲线称为测地线，它定义了非线性的高维流形空间中两点的真实距离[19,34,35]。具体地，定义流形上可微的测地曲线γ:[0,1]→M，其长度表示为

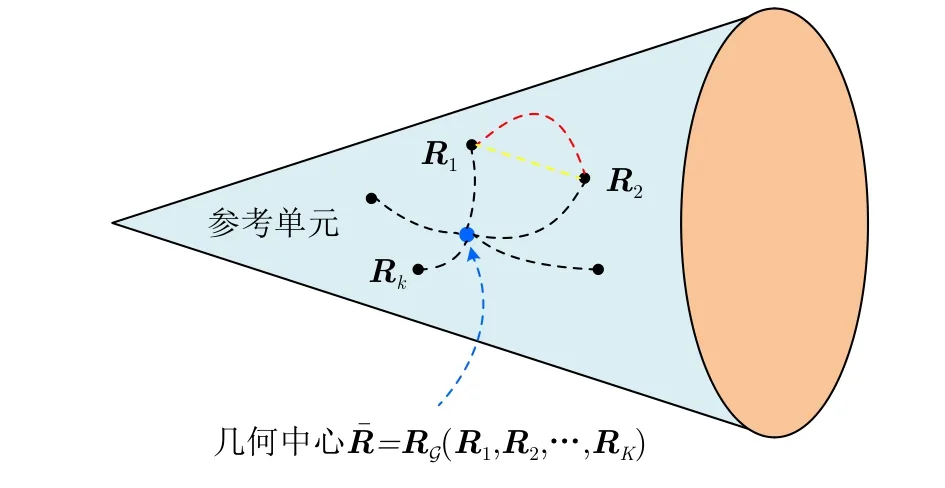
图2 HPD矩阵流形的几何解释Fig.2 Geometric interpretation on HPD matrix manifold

此时，从起始点R1到R2的长度由测地曲线γ(ξ)(0≤ξ ≤1)决定，即

定义1矩阵流形上两点R1,R2的RD定义为切向量κR2的内积，即

除了RD，矩阵流形M上常用的几何距离还有对数欧氏(log-Euclidean,LE)距离，以及KL散度(Kullback-Leibler Divergence,KLD)和Jensen-Bregman类的对数行列式(Log Determinant,LD)散度等[36-39]。不同的距离度量反映着流形不同的几何结构和流形上两点差异，从而影响着流形上目标与杂波的区分性。

在脉冲多普勒雷达中，设计滤波器组是改善目标检测性能的有效方法。由于信号频域的子带滤波在提升信号短时平稳性，抑制带外杂波和改善带内信杂比等方面有一定优势，特别是针对非均匀强杂波背景下的目标检测，采用子带滤波有潜力带来较好效果[11]。因此，本文考虑采用线性相位DFT调制滤波器组实现子带分解，在每个子带对接收的雷达回波信号进行滤波。

其中，|zi-z|表 示两点欧氏距离，表示数据代数均值。区别于欧氏空间中的代数均值，流形空间的几何均值与流形几何结构有关，具体地，对于一组{R1,R2,...,RK}∈M，其均值定义为如下优化问题：

where subscripts‘p’and ‘d’represent‘proportion’and ‘derivative’,respectively,xnand n represent the undamped natural frequency and damping ratio of the system,respectively,and the value of affects the effect of position control,i.e.,>1,over damping;=1,critical damping;0<<1,underdamping.

3 基于正交投影的子带信息几何检测器

3.1 子带滤波

对于分布在矩阵流形上的目标与杂波点，还需研究相应的中心，即几何均值[34,37]。首先，对雷达回波z=(z1,z2,...,zn)T，在传统欧氏空间，其均值可以表示为如下优化问题：

由2.2节可知，矩阵流形上两点的距离度量是目标检测的关键。矩阵流形的黎曼度量为流形上两点的距离，即RD距离，提供了尺度标准。通过定义切空间中切向量的内积，即对于流形上任意一点P ∈M，在其切空间TP M可以定义黎曼度量[34,36]

能力的形成需要习惯的养成，良好习惯的养成要靠我们平时的细心引导。要使学生提高口语交际能力，必须重视成功的范例引导，从小培养学生良好的交际习惯。

其中，h(q)为滤波器的时域表示，Q表示滤波器阶数，线性相位保持目标回波的相位结构不发生改变。通过频率调制，子带滤波器组表示为

本文采用凯撒窗设计原型滤波器，假设滤波器个数M=21,L=10，阶数Q=94，阻带衰减为-40 dB，则DFT调制的子带滤波器组频率幅度响应如图3所示。滤波器组将归一化多普勒频率区间[-0.5,0.5]划分为M个子带区间，每个子带的归一化多普勒频率范围为

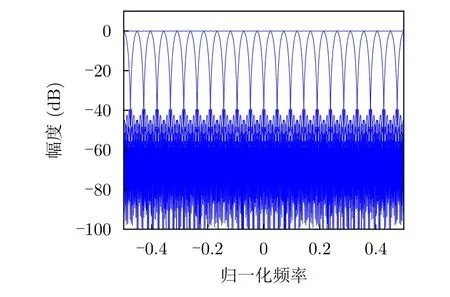
图3 子带滤波器组频率幅度响应Fig.3 Amplitude frequency response of subband filter bank

其中，每个子带(多普勒单元)宽度为 1/(2L+1)。因此，将雷达回波信号的频域划分为多个子带，进行子带滤波，可以表示为卷积形式：

其中，∗表示卷积运算，z表示雷达接收的距离单元回波信号。

3.2 稳健正交投影

3.2.1 基于流形的正交投影

对于子带滤波保留的带内信号，其强杂波信号依旧存在，同样影响着目标与杂波的区分性，进而影响着目标检测性能。因此，本文基于子空间思想[29-31]，提出基于流形的正交投影方法，采用矩阵流形的几何均值估计待检测单元杂波子空间，进行稳健的杂波抑制，以增强目标信号，进而增强与杂波区分性。

首先，根据正交投影定理[40]，假设雷达回波待检测单元zD同时包含着目标信号sD、杂波信号cD和噪声信号nD，则其相关矩阵可以表示为

此时，待检测单元中的杂波信号被抑制，目标信号得到增强。正交投影的关键在于准确估计杂波子空间，可以用待检测单元邻近的参考单元杂波{zk}k∈[K]进行估计。此时，如何准确估计杂波协方差矩阵，是影响正交投影后待检测单元杂波抑制和目标增强效果的关键。

传统正交投影方法主要采用样本协方差矩阵(Sample Covariance Matrix,SCM)估计杂波子空间。具体地，对于参考单元杂波{zk}k∈[K]，其SCM估计表示为

由式(29)和式(16)可知，SCM估计表示K个协方差矩阵的代数均值，为如下优化问题的解：

（1）中国大部分城市大气降尘中重金属元素As、Hg、Cd、Cr、Cu、Ni、Pb 和 Zn 的平均值均高于中国土壤背景值，存在一定程度的污染。Cd在工业区和非工业区中的污染级别最高，污染程度最强。非工业区中的Cd是土壤背景值33倍，主要来自燃煤和车辆尾气；工业区中的Cd超标高达200多倍，主要来自冶炼企业的排放。Cr和Ni的含量在非工业区和工业区中差别不大。

由2.3节可知，协方差矩阵集合{Rk}k∈[K]本质上构成了一个高维的非线性矩阵流形M，基于平坦、线性欧氏空间的代数均值估计未考虑协方差矩阵本质的空间结构特征，在均匀样本数较少时，估计误差较大。而几何均值利用了流形非线性结构特征，具有稳健高效的估计性能，代数均值和几何均值的对比如图4所示。因此，本文基于流形的几何均值估计杂波子空间，即

图4 代数均值与几何均值的对比Fig.4 Comparison between arithmetic mean and geometric mean

并对参考单元存在干扰信号时的鲁棒性进行分析。本文所提的干扰信号为参考单元中包含了类似目标特性的干扰，具有一定多普勒，且信号形式与式(2)相同，会对背景杂波的估计和目标检测带来一定影响。

3.2.2 鲁棒性分析

(3) 正定性：∀x ∈Cn{0},xHRx>0。

挑战盛典现场，一台台曾经或者正在改变世界家电史的创新产品，串联起了海尔33年不断挑战自我、不断战胜极限的历史。随后，由净界自清洁空调、F＋冰箱、防干烧燃气灶以及直驱洗衣机组成的“挑战战队”，与天才美女速算大师李顺实、国际特技记忆大师黄胜华、“黄金舌”中国烹饪大师杨海明、平衡大师韩遂宁夫妇、平衡家庭钟荣芳一家完成了一项项看起来不可能的挑战。

对于K个参考单元杂波协方差矩阵{Rk}k∈[K]，当加入P个干扰信号后，协方差矩阵集合变为{R1,R2,...,RK,C1,C2,...,CP}，其中，{Cp}p∈[P]表示干扰信号的协方差矩阵集合。

其中，υ和µ分 别表示形状参数和尺度参数，Γ (·)和Ψυ-1(·)分别表示伽马函数和修正的贝塞尔函数。在仿真数据实验环境中，设置K分布杂波的形状参数为1和尺度参数为0.5。此外，本文仿真数据和实测数据实验中的信杂比定义为

其中，o表示无穷小。由式(34)可知，影响函数J反映着当干扰信号存在时杂波协方差矩阵均值估计的准确性。代数均值和几种几何均值的影响函数由以下推论给出，具体证明见文献[41]：

推论1当协方差矩阵集合{R1,R2,...,RK,C1,C2,...,CP}的均值为代数均值时，其影响函数为

推论2当协方差矩阵集合{R1,R2,...,RK,C1,C2,...,CP}的均值为RD均值时，其影响函数为

2.1 三组行上腹部手术患者手术时间、麻醉时间比较 三组患者手术时间、麻醉时间比较差异无统计学意义(P>0.05)，见表2。

推论4当协方差矩阵集合{R1,R2,...,RK,C1,C2,...,CP}的均值为KLD均值时，其影响函数为

推论5当协方差矩阵集合{R1,R2,...,RK,C1,C2,...,CP}的均值为LD均值时，其影响函数为

3.3 基于正交投影的子带信息几何检测方法

本文提出的基于正交投影的子带信息几何检测方法流程如图5所示。具体地，对于雷达回波信号{zD,z1,z2,...,zK}，定义复合映射：

图5 基于正交投影的子带信息几何检测流程图Fig.5 Flowchart of subband geometric detection based on orthogonal projection

卫生人才关系到了当地的医疗服务水平乃至地区的发达程度，是卫生服务水平的代表和地区综合竞争力的重要因素[3]。当前医改新政加强了对医疗卫生机构的管理，提高了对医疗卫生人才的要求，对于东丽区而言，亟需建立高效、稳定和可持续发展的卫生人才队伍。首先应当依据人力管理理论和当地医疗卫生事业发展的实际，制定出合理的人才发展规划，加强东丽区卫生人才吸引力，完善后续的人才培养和管理制度，切实提升卫生人才的综合素质。

3.4 计算复杂度分析

本文采用的对比方法包括基于FFT相参积累的CFAR检测方法 (以下仿真实验简称FFT),ANMF,SANMF和RD,LE,KLD和LD度量下的矩阵信息几何检测方法，以及基于最大特征值的检测方法(Maximum Eigenvalue,ME)[42]和一些干扰存在下目标自适应相参积累检测方法，如基于广对称的子空间广义似然比检测器(Persymmetric Subspace Generalized Likelihood Ratio Test,PS-GLRT)和基于部分均匀环境的两步Rao检测(Two Step Rao,2S-Rao)[43,44]。各方法的计算复杂度估计如表1所示。

表1 不同方法的计算复杂度Tab.1 The computation complexity of different methods

4 仿真实验与结果分析

本节主要通过仿真数据和实测海杂波数据实验评估所提方法的性能。在仿真数据实验中，模拟海杂波背景，假设杂波服从K分布；在实测海杂波数据实验中，采用IPIX雷达实测数据和海军航空大学对海探测试验数据进行分析。由于在复杂杂波背景下，杂波呈现非高斯分布，检测概率和虚警概率没有解析表达式。因此，不失一般性，实验采用蒙特卡罗方法评估检测性能。

4.1 K分布仿真数据实验

本文将背景杂波c建模为复合高斯模型，服从K分布，并由球不变随机过程生成，即表示为两个相互独立的随机变量乘积

其中，τ表示缓慢变化的纹理分量，通常建模为伽马分布，g表示快变化的散斑分量，通常建模为零均值复高斯分布。此时，杂波c的概率密度函数为

但大阪总领馆的全力救助，在国内互联网上引发的却是令人意想不到的后果：当部分自媒不负责任地渲染“中国大巴开进机场接人”“中国游客优先上车”等失实细节后，大阪总领馆很快深陷持续质疑。

定义2加入干扰信号后的影响函数J和影响函数值fIF：

算法 1 基于正交投影的子带信息几何检测方法Alg.1 Subband MIG detection method based on orthogonal projection

其中，ϖ表示目标信号幅度参数，ck表示参考单元杂波，n为脉冲数，K为参考单元数。

4.1.1 鲁棒性分析

本节主要分析当存在干扰信号时，几何均值和SCM估计杂波背景的鲁棒性。实验中，设置单个相参处理单元的脉冲数为n=7，参考单元样本总数K=40，加入如式(2)的干扰信号，干扰功率为20 dB，归一化多普勒频率fI=0.25，干扰点数P=20，并采用RD,LE,KLD和LD的几何均值作为对比。通过500次蒙特卡罗分别计算SCM和几何均值估计杂波的平均影响函数值，如图6所示。

图6 加入干扰信号后不同方法的平均影响函数值Fig.6 Mean value of the influence function for different methods after adding interferences

由图6可知，不同干扰数下，SCM估计方法平均影响函数值均较高，几何方法较低，表明干扰的存在对代数均值估计影响最大，几何方法影响最小，鲁棒性更强。特别地，在几何方法中，KLD均值和LD均值估计的平均影响函数值均在10以内，鲁棒性较好。但是，由于LD均值需要迭代计算，复杂度相对较高，而KLD均值只需矩阵求逆，复杂度相对较低[33,37]。

4.1.2 检测性能分析

为分析K分布杂波下不同方法的检测性能，本节的仿真实验环境设置为：假设短脉冲情况，一个相参处理单元内的脉冲数n=7，脉冲重复间隔Tr=1 ms，采用图3所示的子带滤波器。在待检测单元中加入如式(2)的仿真目标，其多普勒频率为200 Hz。同时，为考虑运算时间，假设虚警率Pfa=10-4。为模拟存在干扰信号的场景，在仿真中加入式(2)的干扰信号，干扰数P=2，干扰功率为20 dB，多普勒频率fI=250 Hz。

本节主要对比不同杂波参考单元数(K=n和K=2n)下各方法的检测性能。由图7和图8可知，所有方法检测性能均随着杂波参考单元数增加而提升，并且本文所提方法性能均优于各对比方法。具体地，当K=n时，由于杂波参考单元数较少，影响协方差矩阵估计精度，自适应匹配滤波类和2SRao方法性能严重下降，趋近于0，但PS-GRLT方法展现出相对较好性能。此时，当检测概率达到0.8时，本文所提方法较FFT提升约1 dB，较ME提升约4 dB，较KLD提升约6 dB，较PS-GLRT方法提升约9 dB。当K=2n时，本文所提方法相比于SANMF和PS-GLRT方法提升分别约3 dB和8 dB，相比于FFT和ME方法提升约4 dB，同时，还比几何方法中最好的KLD提升约6 dB。特别地，由图7、图8可知，RD和LE的性能几乎一致。

图7 K分布杂波下的检测概率(K=n)Fig.7 Probabilities of detection for K distribution clutter (K=n)

图8 K分布杂波下的检测性能曲线(K=2n)Fig.8 Probabilities of detection for K distribution clutter (K=2n)

4.2 实测数据实验

本节的实测海杂波数据主要采用IPIX雷达实测数据和海军航空大学对海探测试验数据。

4.2.1 IPIX实测数据

首先，采用加拿大McMaster大学IPIX雷达采集的海杂波数据进行仿真分析，数据文件名为19980204_155537_ANTSTEP[45]，这里主要考虑HH极化，数据的具体参数信息如表2所示。

尾气排放超标的在用汽车应当委托具有相应资质的维修治理站(M站)进行维修治理。M站应当按照国家、行业和当地的有关技术规范进行维修，维修竣工合格后，通过I/M制度信息管理系统及时上传维修记录和数据，并出具维修竣工出厂合格证。车主凭维修竣工出厂合格证到检测站(I站)进行复检。

表2 数据文件19980204_155537_ANTSTEP参数Tab.2 Parameters of data file 19980204_155537_ANTSTEP

分析该数据集的杂波功率谱，如图9所示。从图9(a)可以看出，由于海面的运动，海杂波具有一定的多普勒，相应强杂波区域的多普勒频率约为160 Hz和-160 Hz，3 dB宽度约为120 Hz。同时，图9(b)的距离-多普勒三维图也直观地反映了该组海杂波数据具有非均匀性。

本研究40例膝关节损伤患者相关数据应用SPSS19.0软件对比分析，MRI检查与CT检查膝关节积液、半月板损伤、韧带损伤、骨质损伤等检出情况行χ2检验，采用（n%）表示。组间对比差异性较高（P＜0.05），本研究结果有统计学意义。

图9 数据集杂波谱Fig.9 Clutter power spectrum of the data set

本节实验同样考虑短脉冲序列条件，设置一个相参处理单元的脉冲数n=7，参考单元数K=2n，并且在待检测单元左右各设置2个保护单元。由于该数据集不存在目标，因此，本节在第10个距离单元加入如式(2)的目标信号，并考虑目标淹没于强杂波区和远离强杂波区两种情况，即假设目标多普勒频率分别为fd=160 Hz和fd=350 Hz。同样地，在仿真中加入如式(2)的干扰信号，干扰数P=2，干扰信号功率为20 dB，多普勒频率fI=250 Hz。由于数据集脉冲数有限，仿真假设虚警概率Pfa=10-3，并利用前56000组杂波数据计算检测门限，利用后4000组杂波数据计算检测概率。

首先，为验证所提方法性能，假设目标淹没在主杂波区域的情形，如图10所示。具体地，本节在第10个距离单元加入多普勒频率fd=160 Hz的运动目标，信杂比为5 dB，并基于IPIX雷达海杂波数据集，计算目标淹没于强杂波背景的归一化检测统计量。在每个距离单元取1000个连续脉冲单元，分为142个相参处理单元，每个相参处理单元的长度为n=7，则可以计算得到28×142个归一化检测统计量。图10(a)给出了原始数据的归一化距离-脉冲二维图，可以看到杂波背景是非均匀的，并且目标单元周围存在强杂波，容易在检测时带来虚警。图10(b)到图10(i)给出了现有方法的处理结果，可以看到FFT,ME,KLD,LE和2S-Rao方法处理后均残留着一定的强杂波，其中，PS-GLRT方法对杂波抑制效果最好，但目标也同样被抑制，无法检测。特别地，ANMF和SANMF处理后强杂波带来的虚警最多，这导致其性能严重下降，主要原因是实际中自适应匹配滤波类方法需要进行多普勒扫描，由于脉冲数少，扫描后用于匹配的最佳多普勒频率与信号模型相差大，存在一定失配，导致性能下降。由图10(j)可知，本文所提方法具有最少的强杂波干扰，能够实现较好的强杂波抑制，并增强目标成分，有利于获得较好的检测性能。因此，以上对比结果验证了所提方法在目标淹没于非均匀强杂波时的性能优势。

图10 IPIX雷达数据的归一化检测统计量(fd=160 Hz)Fig.10 Normalized detection statistics of the IPIX radar data (fd=160 Hz)

为进一步评估所提方法的检测性能，本节考虑了fd=160 Hz(目标淹没于强杂波区)和fd=350 Hz(目标远离强杂波区)两种情形。图11和图12分别给出了相应的检测性能曲线。由图11和图12可知，各个方法在当目标远离强杂波区时的性能均优于淹没于强杂波区，其中，PS-GLRT和2S-Rao方法性能最差，本文所提方法在两种情形下均具有最优的检测性能。具体地，当fd=350 Hz时，本文所提方法性能最好，且当检测概率达到0.8时，相比于FFT提升约9 dB，相比于ME和ANMF提升约7 dB，比KLD提升约5 dB。当fd=160 Hz时，本文所提方法检测性能相比于FFT,ME和SANMF提升约1.5 dB，相比于ANMF提升约6.5 dB，相比于KLD提升约4 dB。同时，对比图11和图12，ANMF和SANMF在目标淹没于杂波时性能严重下降，但SANMF始终优于ANMF，原因是信号子带滤波具有抑制带外杂波，保留带内目标信号的效果，从而减少了性能损失，也间接说明了子带滤波对改善检测性能具有好处。此外，该实测数据同样验证了RD和LE具有相同性能，并且在几何方法中KLD性能最好。因此，后续实验中主要用基于LE和KLD度量的几何方法进行对比。基于IPIX雷达实测数据的仿真分析，验证了本文所提方法性能的优越性和稳健性，特别是当目标淹没于强杂波时仍然能够保持较好的检测性能。

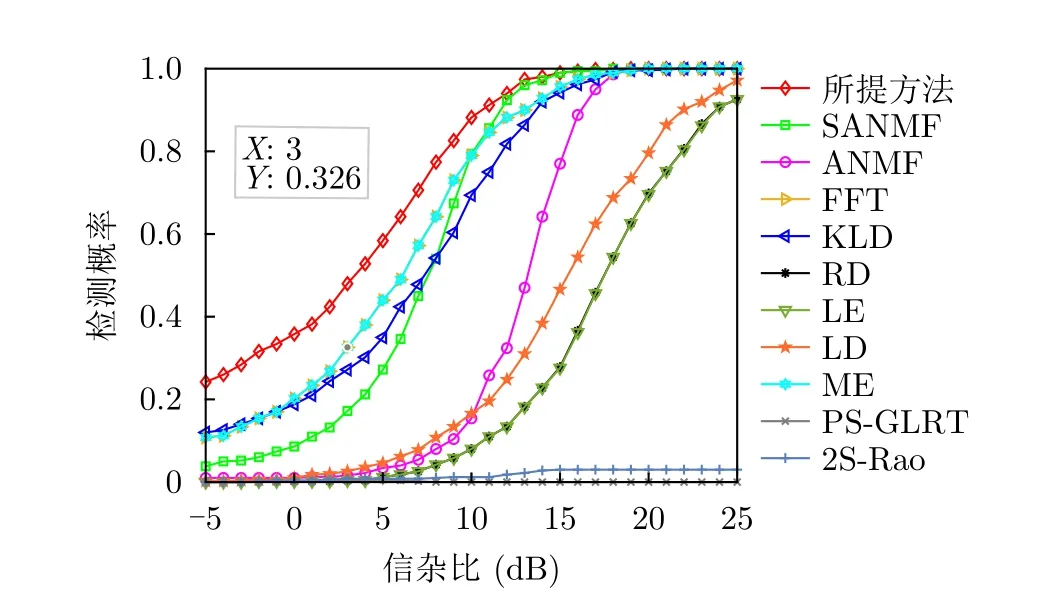
图11 基于IPIX雷达数据的检测概率(fd=160 Hz)Fig.11 Probabilities of detection for the IPIX radar data (fd=160 Hz)

图12 基于IPIX雷达数据的检测概率(fd=350 Hz)Fig.12 Probabilities of detection for the IPIX radar data (fd=350 Hz)

4.2.2 海军航空大学实测数据

基于海军航空大学(Naval Aviation University,NAU)针对雷达海上目标探测关键技术攻关对雷达实测数据的迫切需求开展的“雷达对海探测数据共享计划”，本节利用雷达学报网站“雷达对海探测数据”2020年第1期数据进行仿真分析[46]，所用数据集的文件名为20210106150614_02_staring。此数据集是在海杂波与目标探测数据采集试验中用X波段固态功放监视/导航雷达凝视时所采集的，试验场景如图13所示[47]。数据集中存在弱小目标(航道浮标)，具体参数信息如表3所示。同时，该数据集的距离-脉冲二维图如图14所示，可以看到由于强海杂波和芝罘岛的影响，目标几乎淹没在杂波中。

表3 数据文件20210106150614_02_staring参数Tab.3 Parameters of data file 20210106150614_02_staring

图13 海杂波与目标探测数据采集的试验场景Fig.13 Sea clutter and target detection experimental scenario

图14 数据集20210106150614_02_staring的归一化距离-脉冲图Fig.14 Normalized range-pulse of data set 20210106150614_02_staring

首先，为避免固定芝罘岛的杂波影响，本节取数据集前2000个距离单元(前5.44 km)，每个距离单元前70个脉冲作为实验数据，即对2000×70的数据进行仿真验证，其中，目标位于第1763单元(4.84 km处)，如图15所示。从图15可以看出，近距离(前2.5 km)强海杂波的存在极易给目标检测带来虚警。

图15 NAU实验数据(目标位于4.84 km处)Fig.15 Experimental data of NAU (the target is located at 4.84 km)

图16给出了不同方法的归一化检测统计量。由图16可知，FFT,ME和几何方法处理效果接近，均能在一定程度上增强目标，但背景杂波抑制效果不佳，虚警相对较多。对于ANMF和SANMF方法，目标淹没在强杂波中，强杂波将带来较多虚警，很难实现目标检测，效果最差。相比于图16(a)到图16(f)的方法，本文所提方法具有最好的性能，背景杂波抑制效果较好，并无强杂波成分，且目标被明显增强，意味着在虚警概率较高时也能够取得较好的检测性能。同时，图17给出了各方法的归一化一维距离像，可以明显看到，相比于其他对比方法，本文所提方法使得4.84 km处目标增强的同时，其余各个距离的杂波被显著抑制，进一步验证了所提方法的有效性。

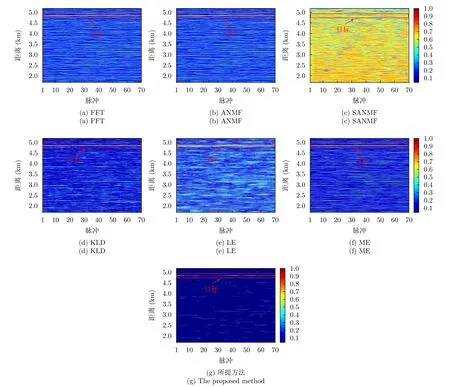
图16 NAU数据的归一化检测统计量Fig.16 Normalized detection statistics of the NAU data

图17 归一化一维距离像Fig.17 Normalized range profile

此外，基于NAU的实验数据，图18给出了本文所提方法和其他对比方法的接收机工作特性(Receiver Operating Characteristic,ROC)曲线，与图16结果相对应。由图18可知，在不同虚警率下，所提方法均具有最好性能，并且FFT,ME和几何方法具有相近的性能，但均劣于本文所提方法。而PS-GLRT,2S-Rao,ANMF和SANMF方法只有在高虚警概率下才具有较高的检测概率，性能较差。因此，通过对比ROC曲线，也验证了所提方法对于强杂波背景下的弱小目标检测具有较好的性能。

5 结语

本文针对复杂强杂波背景下的雷达弱小目标检测问题，提出了一种基于正交投影的子带信息几何检测方法，以改善复杂背景下弱小目标的检测性能。本文所提方法利用了子带分解实现雷达回波带外杂波抑制，提升了带内信号的短时平稳性，并采用矩阵流形的几何均值估计子带内杂波信号子空间，提出了基于流形的正交投影方法，有效地抑制了强杂波，最终增强了目标与杂波的区分性。仿真数据和实测海杂波数据实验表明，所提方法对参考单元中的干扰信号具有鲁棒性，并在非均匀的强杂波背景下具有良好的性能。同时，当目标淹没于强杂波区和远离强杂波区时，所提方法均能取得较好的检测性能，并优于几类典型的检测方法。下一步工作计划考虑研究具有CFAR或者渐进CFAR特性的信息几何检测器。