渗流和溢流导致冰碛坝溃决的数值分析

王亚妮，刘德高，董千里，申国强

（1.淮安市水利勘测设计研究院有限公司，江苏 淮安 223005；2.水发规划设计有限公司，山东 济南 250014；3.承德水创工程项目咨询有限公司，河北 承德 067000）

1 冰碛坝溃决成因

受气候变化影响，新疆的冰川区常因冰湖溃决洪水（GLOF）引起洪水和泥沙灾害[1]。冰湖溃决通常是由于渗漏和湖水溢出侵蚀大坝，引起冰碛坝破坏而发生的。冰碛坝相对较弱，可能会突然破裂，导致大量水和沉积物突然排放，造成下游地区的灾难性洪水，对群众的生命、财产、土地和基础设施造成严重破坏[2]。为了避免和最大程度地减少群众生命财产损失，迫切需要一种机制方法来研究冰湖溃决事件及洪水对下游的影响机制。

受到客观条件的限制，对冰湖溃决事件及其下游洪水的研究非常有限。目前冰湖溃决的研究主要集中在卫星观测、历史记录和预防措施等方面，而对冰碛坝的破坏机理和侵蚀过程仍缺乏深入的认识[3]。学者们通过收集已有的冰湖溃决事件中的相关资料建立了经验模型，以预测冰湖溃决的洪峰流量与湖泊体积、深度和面积的关系，并建立了物理模型来计算冰湖溃决的特征[4]。此外，洪峰流量取决于坝体特性、破坏机制、泥沙特性等多种因素，而这些因素并不包含在经验关系式中。NWS-BREACH、HEC-RAS 溃坝模型等物理模型通常用于预测冰湖溃决的出流过程线，但这些模型的局限性在于没有考虑坝面边坡破坏、坝面切头和侧向侵蚀等实际机制[5-6]。此外，一些冰湖溃决事件的下游淹没或影响可通过洪水演进模型进行研究，这些模型均未考虑河床泥沙颗粒的冲淤过程。

冰碛坝和滑坡坝是多种颗粒大小不等的非均质混合物。冰碛坝与通常的天然坝并无实质区别，冰碛坝被视为天然坝的一种。因此，即使在冰碛坝的情况下，也可以采用与滑坡坝相同的试验和计算处理[7]。本研究建立了一个数值模型来计算由于渗流和溢流破坏冰碛坝而导致的冰湖溃决的特征，并对渗流和冰碛坝破坏进行了数值分析。为了计算冰碛坝的孔隙水压力和大坝的边坡稳定性，将渗流模型和边坡稳定性模型合并到流量和坝面侵蚀的数值模型中，并将模拟结果与实验结果进行比较。

2 数值模型

2.1 渗流模型

渗流是引起冰湖溃决的主要因素，Richards 方程是描述渗流过程的基本控制方程，可用于模拟非均质土体饱和-非饱和渗流过程。因此，本文通过使用混合格式的Richards 方程计算冰碛坝非饱和土壤的孔隙水压力变化，冰碛坝非饱和土壤孔隙水压力变化Richards方程计算公式如下：

式中：ψ——压力水头，m；

Kx和Kz——x 和z 方向的水力传导率，m/s；

C——比湿容量；

θ——土壤的体积含水量，%

x——水平空间坐标，m；

z——向上为正的垂直空间坐标，m；

t——时间，s。

蓄水系数与渗透系数的关系对于使用公式计算非饱和土壤系统中的水分运动非常重要。本文给出了广泛使用的van Genuchten 本构关系进行了冰碛坝中的渗流分析，计算了储水系数、渗透系数和比湿容量，如：

式中：Se——有效饱和度；

θs、θr——分别为泥沙混合物的饱和含水率和残余含水率，%；

α、η——为与土壤基质势有关的参数，通过使用土壤-持水曲线的曲线拟合确定；

ψ——压力水头；

Ks——饱和导水率，m/s；

m——1-1/η。

此外，Brooks 和Corey 提出的本构关系给出了储水系数，渗透系数和比湿容量的描述：

式中：ψb——空气进入值；

λ——孔径分布指数；

δ——经验常数。

通过渗流模型计算的不同案例含水率模拟值见表1。

表1 含水率模拟值汇总

2.2 边坡稳定性模型

许多研究人员使用简化的Janbu 方法来计算滑移表面的安全系数Fs，如下：

式中：c——坝体材料的内聚力，N/m2；

li——每个切片底部的长度，m；

α——每个切片底部的斜率；

Wi——每个切片包括地表水的重量，N；

uwi——每个切片底部的平均孔隙水压力，N/m2；

φ——内摩擦角，°。

简化的Janbu 方法未考虑非饱和土壤中产生的负孔隙水压力。负孔隙水压力导致剪切强度增加。因此，非饱和土的抗剪强度（τ）定义为：

式中：σn——总法向应力，N/m2；

ua——孔隙气压，N/m2；

uw——孔隙水压力，N/m2。

通过使用剪切强度方程方程，滑移面的安全系数可以定义为：

式中：Pi——第i 个切片的大气压强；

uαi——第i 个切片的孔隙气压；

mαi——第i 个切片底部的重量。

考虑吸力和不考虑吸力的边坡稳定性模型模拟的滑动面模拟结果如表2 所示。

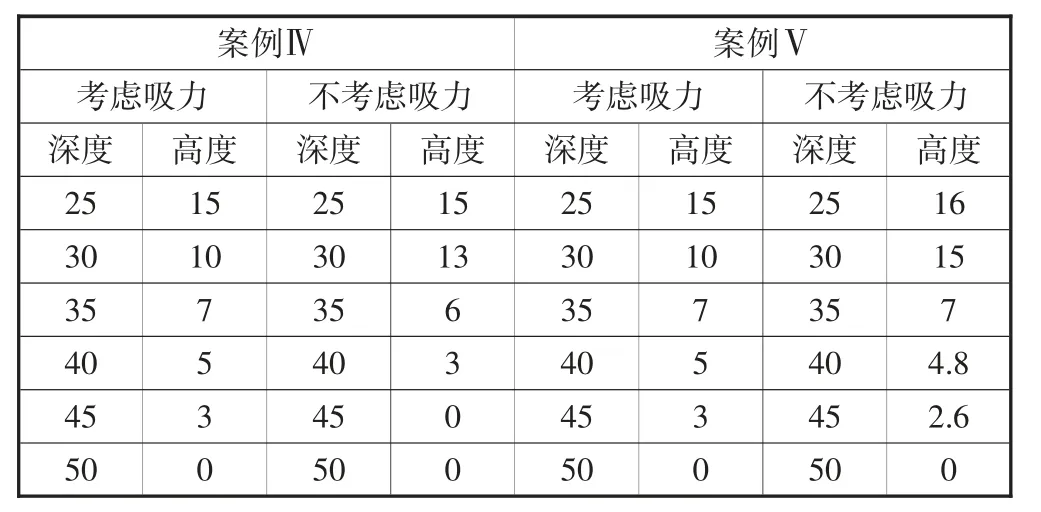
表2 滑动面模拟结果

2.3 流动和侵蚀模型

泥沙-混合流的二维动量方程、水流的连续性方程和泥沙颗粒的连续性方程可以表示为：

式中：M——x 方向上每单位宽度的流量，m3/s；

N——y 方向上每单位宽度的流量，m3/s；

u——x 方向上的速度分量，m/s；

v——y 方向上的速度分量，m/s；

h——流动深度，m；

zb——原始床高程测得的侵蚀或沉积厚度，m；

θbx0——原始床面坡度x 分量，°；

θby0——原始床面坡度y 分量，°；

ib——侵蚀/沉积速度，m/s；

c——水流中泥沙浓度，kg/m3；

c*——河床中的最大泥沙浓度，kg/m3；

β——动量修正系数；

g——由于重力引起的加速度，m/s2；

ρT——泥沙密度，kg/m3；

τbx——x 方向的底部剪切应力，N/m2；

τby——y 方向的底部剪切应力，N/m2；

sb——河床中的饱和度；

q——渗透率，m/s。

通过考虑吸力的影响，侵蚀速度ib描述为：

式中：K——常数；

θb——河床斜率；

σ——泥沙质量体积比；

Δτsuc——由于吸力引起的剪切应力增量，N/m2；

ρm——平衡沉积物密度；

dm——平均粒径，mm；

c∞——平衡沉积物浓度；

ρw——孔隙流体密度。

坝面侵蚀的模拟结果如表3 所示：

表3 坝面侵蚀模拟结果

3 水槽实验

水槽实验是用模型模拟试验，收集试验参数，对工程实验结果进行参照对比。试验采用长500 cm、宽30 cm、深50 cm 的水槽（见图1），坝体采用石英砂（泥沙混合物1 和2）制作，两种类型的泥沙混合物用于不同粒度的结果比较。

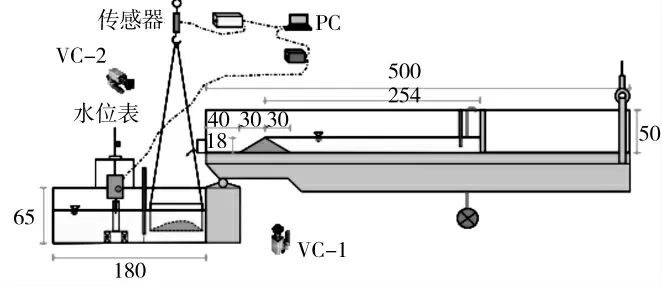
图1 水槽实验示意图（单位：cm）

图2 和图3 分别显示了粒度分布曲线和坝体的详细信息。泥沙混合物1 和2 的平均粒径分别为1.4 mm 和1.04 mm，最大粒径为4.75 mm，泥沙质量体积比为2.65 g/cm3。

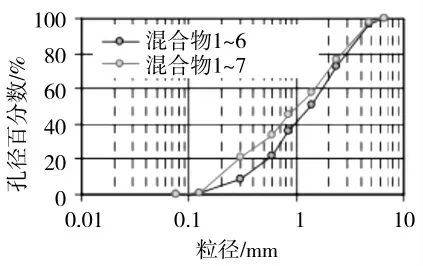
图2 泥沙混合物粒度分布曲线

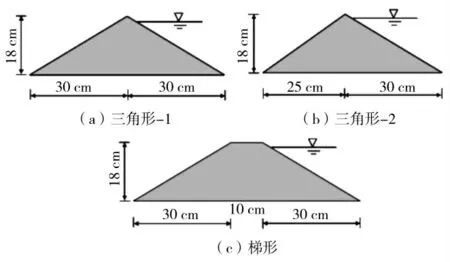
图3 不同坝体的详细信息

通过从湖泊上游端供给恒定的排水量来填充湖水。当水位上升漫顶而导致冰碛坝溃决时，不断从湖的上游端向坝顶供水并侵蚀。然而，在冰碛坝渗漏溃决的情况下，通过从湖泊上游端供给恒定的排水量，湖水被填满的深度约为16 cm。实验条件见表4。

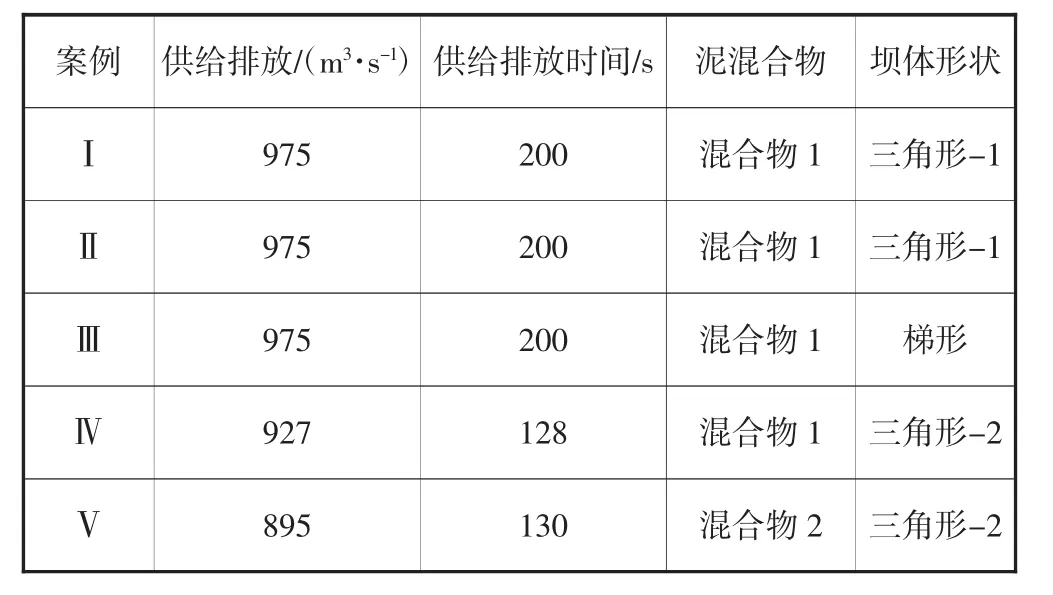
表4 实验条件汇总表

4 成果分析

含水量反射计（WCR）测量的坝体中的水分运动如图4 所示。图5 显示了湖泊中测得的水深随时间的变化。van Genuchten 本构关系的土壤参数值（泥沙混合物1 和2：α=6.3，η=3.1 和α=4.0，η=3.2）。Brooks 和Corey 本构关系的土壤参数值（泥沙混合物1 和2：λ=2.5，ψ=-0.19 和λ=1.8，ψ=-0.19）。这均是使用两种混合物的土壤-持水曲线拟合确定的。Ks=0.000 5 m/s 和θs=0.312 为泥沙混合物1 的测量值，Ks=0.000 25 m/s和θs=0.296 为泥沙混合物2 的测量值。

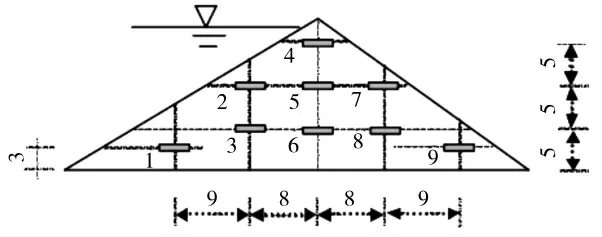
图4 坝体中含水量反射计（WCR）1~9 的位置（单位：cm）

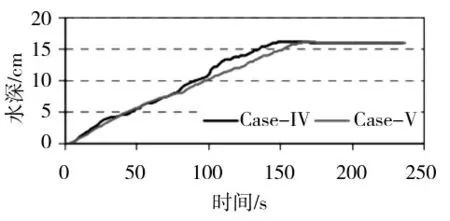
图5 湖泊水深随时间的变化

图6 和图7 分别显示了案例IV 和案例V 坝体中的模拟水分分布和实验水分分布。图中，t=0 是湖泊上游端供水的开始时间，坝体中的水分运动是由于上游湖水的深度所致。通过使用Brooks 和Corey 关系计算的坝体水分运动速率比实验值快。非饱和土壤中的导水率在Brooks 和Corey 关系式中高于van Genuchten函数。采用van Genuchten 函数本构关系的模拟结果比采用Brooks 和Corey 本构关系的模拟结果与试验结果更吻合。储水系数与渗透系数的关系对非饱和区域水分运动的计算非常重要。坝内水分运动还取决于饱和导水率。泥沙混合物2 的细颗粒泥沙含量高于泥沙混合物1 的细颗粒泥沙含量，泥沙混合物2 的水力传导率较小，水分运动较泥沙混合物1 的慢。

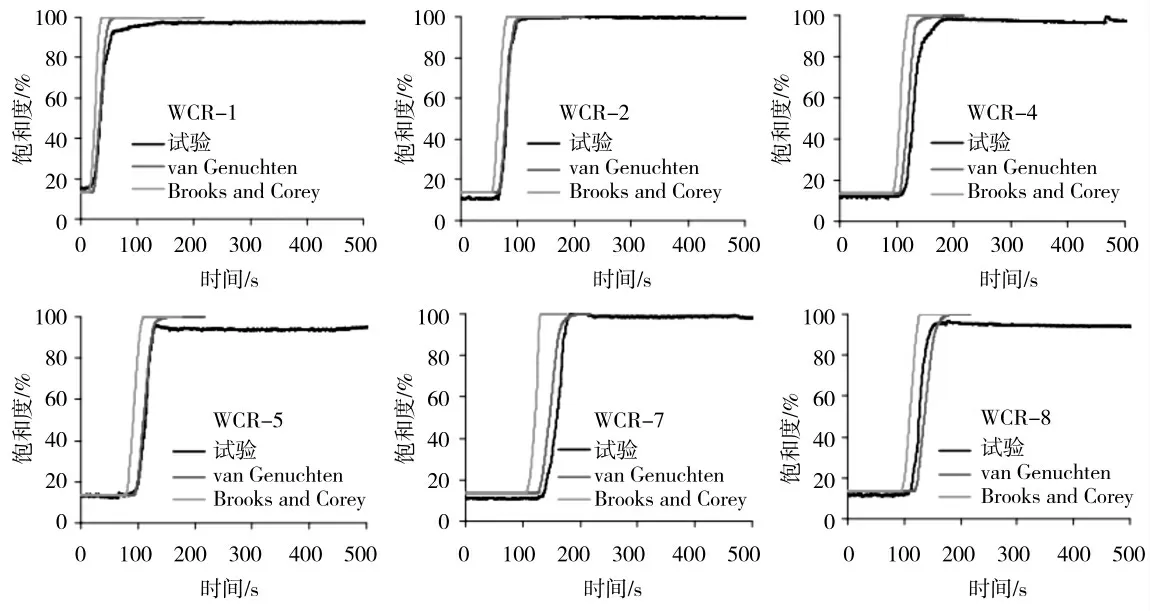
图6 案例IV 泥沙混合物1 下模拟和实验水分含量曲线的比较

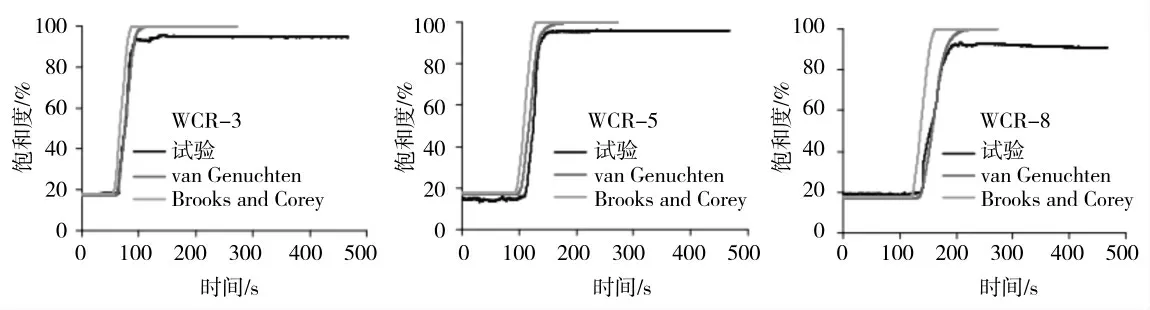
图7 案例V 泥沙混合物2 下模拟和实验水分含量曲线的比较

图8 给出了考虑吸力和不考虑吸力（Janbu 的简化方法）的土体抗剪强度中渗流引起的冰碛坝溃决模拟滑动面与试验滑动面的对比。利用van Genuchten函数关系式计算土壤中的水分运动，采用动态规划法计算临界滑动面。边坡稳定性分析中考虑吸力的模拟破坏面比Janbu 简化方法更符合试验结果。在非饱和土中，破坏一般表现为浅层破坏面。在边坡稳定性分析中不考虑基质吸力的影响，可能会出现深部破坏面。因此，在非饱和坝体边坡稳定性分析中，需要考虑基质吸力作用下的非饱和抗剪强度。泥沙混合物1 的破坏面比泥沙混合物2 更深，这可能是由于泥沙混合物2 中吸力的作用更大。

图8 冰碛坝的模拟和实验滑动面对比

为了计算冰碛坝破坏的溃决流量，以下采用van Genuchten 函数关系式进行渗流计算，并考虑非饱和土中的吸力进行边坡稳定性分析。图9a 为溢流（案例I）导致冰坝溃决的水槽下游端溃决流量的模拟和试验结果。此时，坝体内初始含水率约为0.21%。图9b 为坝内初始含水率为5.54%的溢流冰碛坝溃决结果，坝内初始含水率为5.54%时的洪峰流量较高。梯形坝形情况下溃决流量的相似结果如图9c 所示。发现三角形坝形情况下的洪峰流量高于梯形坝形。三种情况下泥沙排出量的模拟结果与实验结果一致。坝面侵蚀还考虑了土体中吸力的影响，溢流对冰碛坝的侵蚀也通过数值模拟模型得到了很好的解释。

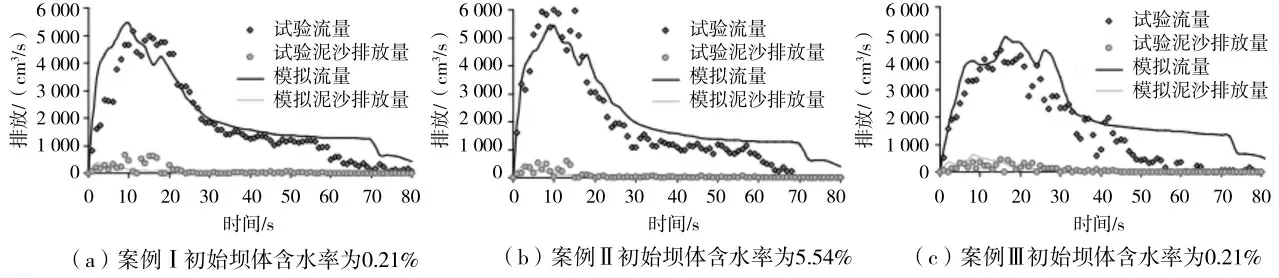
图9 溢流溃决导致冰碛坝溃决的溃决流量

图10 为泥沙混合物1～6 和1～7 在冰碛坝渗流情况下溃决流量的模拟和试验结果。冰碛坝溃决后，湖水立即漫过坝面并侵蚀坝面，导致湖水快速下降。泥沙混合物1～6 的峰值流量高于泥沙混合物1～7。在冰碛坝溃坝渗流破坏的情况下，溃决流量的模拟结果与试验结果一致。模拟结果与实验结果的对比表明，本文采用的二维流动与侵蚀模型计算结果稳定可靠，所提出的模型可用于计算冰川溃决导致冰湖溃决的渗流和溢流特征。

图10 冰碛坝渗流破坏引起的模拟和实验流量

5 结论

通过数值分析计算由渗流和溢流引起的冰碛坝溃决的特征。使用van Genuchten 函数计算的水分廓线与实验水分廓线更加吻合。边坡稳定性分析中考虑吸力的模拟破坏面比不考虑吸力的Janbu 简化方法给出的结果更精确。溃决流量和坝面侵蚀的结果也与试验结果一致。湖泊溃决流量的突然释放可能会造成下游洪涝等灾害的发生。