十字形内置破片定向战斗部破片的飞散特性*

李 鑫，王伟力，梁争峰，畅 波，苗润源

（1.海军工程大学兵器工程学院，湖北 武汉 430033；2.西安近代化学研究所，陕西 西安 710065）

现代战争中，在定点杀伤目标的同时尽量减少对周围非目标人员和设施的附带毁伤，不仅是人道主义的体现，也是对反恐作战、维和任务等的基本要求[1-3]。

目前，在低附带毁伤弹药的研究和应用方面，主要采用高密度惰性金属弹药[4-6]，即在高能炸药中加入粉末状、高密度惰性金属，此方法主要通过控制毁伤距离实现低附带毁伤。另一种方法是通过控制毁伤角度实现对定向区目标的高效毁伤和非定向区的零毁伤，在拦截弹道导弹时采用的破片芯式战斗部[7-9]就是采用的这种方法，将破片放置于战斗部正中心，周围布设分块装药，且在分块装药之间布设隔离层，用于防止邻近装药发生殉爆，当引信探测到目标方位时，将目标相对方向的分块装药起爆，此时芯部毁伤元向着目标方向飞散，毁伤元利用率较高。但由于分块装药与芯部毁伤元装填比较低，速度很小，因此该战斗部主要利用弹目相对速度毁伤高超声速目标，若要对人员及轻型车辆类目标造成有效毁伤，实现低附带毁伤，则需要适当提高芯部破片的速度。

本文中基于破片芯式战斗部，设计一种十字形定向战斗部，并简要分析其作用机理，探讨两种起爆模式下战斗部的破片飞散速度、径向飞散角度等性能，并建立破片飞散速度的理论计算模型。

1 十字形内置破片定向战斗部

1.1 结构设计

十字形内置破片定向战斗部结构如图1 所示，主要由壳体、分块装药、扩爆药、钨球、聚氨酯、铝衬等组成。其中，壳体与铝衬通过焊接连接形成基本骨架，钨球内置于铝衬之间，分块装药浇注于壳体与铝衬之间，且装药与铝衬之间涂覆聚氨酯，分块装药置于一个封闭的腔体内。分块装药选择爆轰感度较低且具备较强金属加速能力的HMX 基PBX 炸药，钨球既是毁伤元，同时与铝衬、聚氨酯一并作为复合隔爆层，可有效避免相邻分块装药发生殉爆。

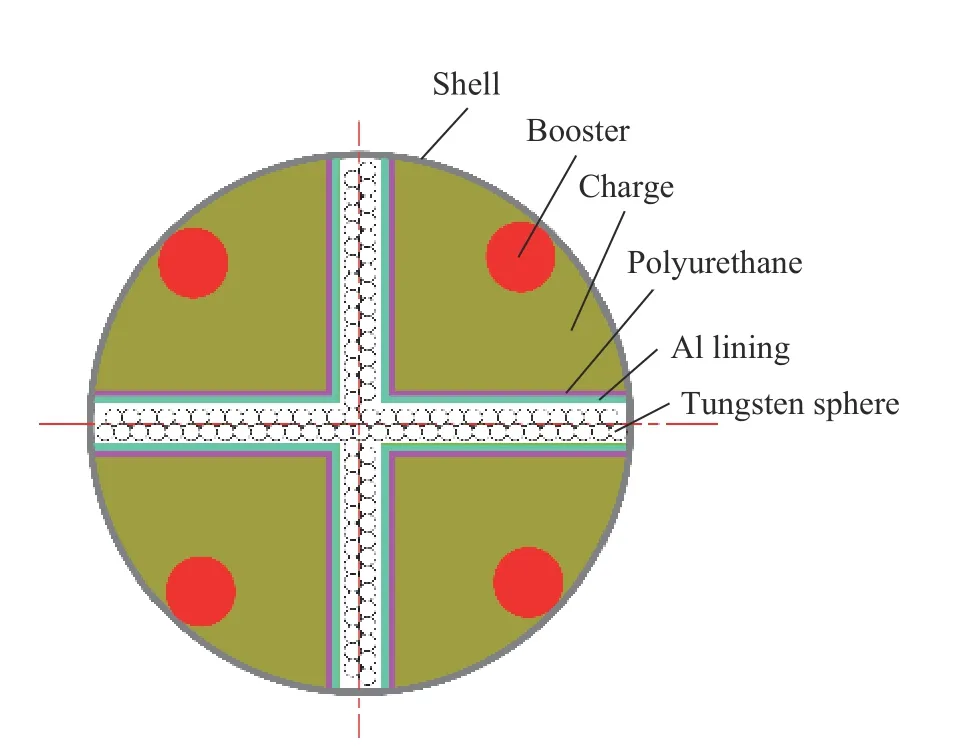
图1 十字形内置破片定向战斗部结构示意图Fig.1 Schematic diagram of the cross-shape built-in fragmentation directional warhead

战斗部直径80 mm、长100 mm，由于战斗部两端端盖厚度达到一定值时可以消除稀疏波的影响[10]，为忽略轴向速度分布的差异，战斗部两端端盖采用15 mm 厚的硬铝合金，内部装填2 列相切排布的钨球，单个钨球的直径为2.5 mm、质量约0.15 g，钨球总共3 570 枚，单个分块装药质量约0.1 kg，总装药质量约0.4 kg。

1.2 作用机理

利用目标距离或角度信息计算出引爆点，引信由全电子安执及激光探测装置两部分组成，激光探测装置的8 个探测窗口与4 个起爆点（编号1#～4#）的相对位置如图2 所示。8 个探测窗口将战斗部分为8 个区域（Ⅰ～Ⅷ），依据目标位置不同，起爆不同区域的分块装药，实现破片定向毁伤。作用模式主要分为两种：当探测窗口捕捉的目标位于区域Ⅰ、Ⅲ、Ⅴ、Ⅶ中任一象限时，与其相对方向的相邻两点同时起爆（例如：目标位于区域Ⅰ时，起爆点2#、3#同时起爆），其余两个区域的装药不起爆；当探测窗口捕捉的目标位于区域Ⅱ、Ⅳ、Ⅵ、Ⅷ中任一区域时，与其相对方向的相邻三点同时起爆（例如：目标位于区域Ⅱ时，起爆点2#、3#、4#同时起爆），其余一个区域的装药不起爆。

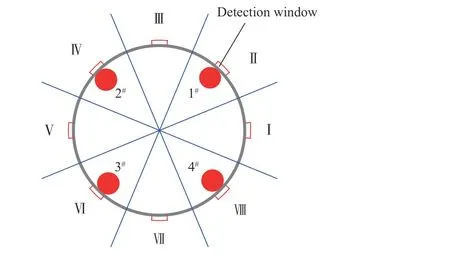
图2 激光探测装置的8 个探测窗口与4 个起爆点的相对位置Fig.2 The relative positions of the eight detection windows of the laser detection device and the four detonation points

两种起爆模式下破片的定向飞散如图3 所示。相邻2 点起爆时，一字形内破片进入目标区域，破片数量占总破片数的50%，破片径向飞散角不超过180°；相邻3 点起爆时，∨字形内破片进入目标区域，破片数量占总破片数的50%，破片径向飞散角不超过90°。将破片径向飞散区域定义为定向杀伤区，剩余区域定义为低附带安全区。

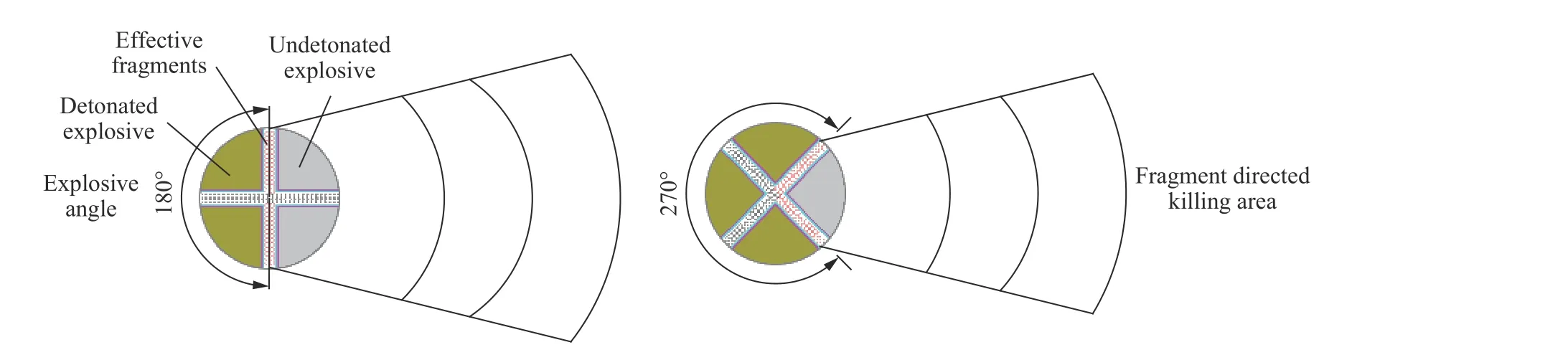
图3 两种起爆模式下破片飞散示意图Fig.3 Schematic diagrams of fragments dispersion under two different initiation modes

2 数值模拟

2.1 计算模型及材料参数

采用LS-DYNA 动力学模拟软件分析两种起爆模式下炸药的爆轰加载过程及破片径向分布的运动特性，计算模型由壳体、钨球、内衬、聚氨酯、炸药和空气6 部分组成，如图4 所示。战斗部壳体、钨球、内衬和聚氨酯采用单点积分Lagrange 六面体网格建模，单元使用Lagrange算法；炸药和空气采用Euler 六面体网格建模，单元使用单点Euler 算法；采用单层网格三维多物质流固耦合MMALE 算法耦合计算，空气边界采用无反射自由边界条件，并对模型整体各节点施加Z方向约束条件。网格尺寸为0.5 mm，采用cm-g-µs 单位制建模。

图4 数值计算模型Fig.4 Numerical calculation model

炸药采用JWL 状态方程和MAT_HIGH_EXPLOSIVE_BURN 爆轰模型共同描述，JWL 状态方程是由实验方法确定的状态方程，能精确地描述在爆炸驱动过程中爆轰产物的压力、能量与体积膨胀特性，其表达式为：

式中：v为爆轰产物相对比容，E为炸药初始内能，A、B、R1、R2和ω 为表征炸药爆轰特征的常数，HMX 基PBX 炸药材料参数如表1 所示[11]。

表1 HMX 基PBX 炸药的材料参数Table 1 Material parameters of HMX-based PBX explosives

壳体及内衬材料均为2A12 铝合金，均采用Johnson-Cook 本构模型和Grüneisen 状态方程共同描述，这两种模型能够较好地描述材料的应变硬化效应、热软化效应、损伤累积效应，其中Johnson-Cook 材料模型的断裂由累积损伤参数D表示，当D=1 时发生破损，将材料单元删除。2A12 铝合金材料参数如表2所示。

表2 2A12 铝合金的材料参数Table 2 Material parameters of 2A12 aluminum alloy

钨球材料为93W 合金，采用PLASTIC_KINEMATIC 随动硬化模型，其参数如表3 所示[12]。

表3 93W 合金的材料参数Table 3 Material parameters of 93 W tungsten alloy

聚氨酯采用*MAT_ELASTIC_PLASTIC_HYDRO 模型和Grüneisen 状态方程描述，其参数如表4 所示[13]。

表4 聚氨酯的材料参数Table 4 Material parameters of polyurethane

空气采用*MAT_NULL 模型和线性多项式状态方程描述，理想气体状态方程为：

2.2 破片驱动过程及飞散特性

图5～6 给出了相邻2 点起爆、相邻3 点起爆下不同时刻破片径向飞散分布图像。

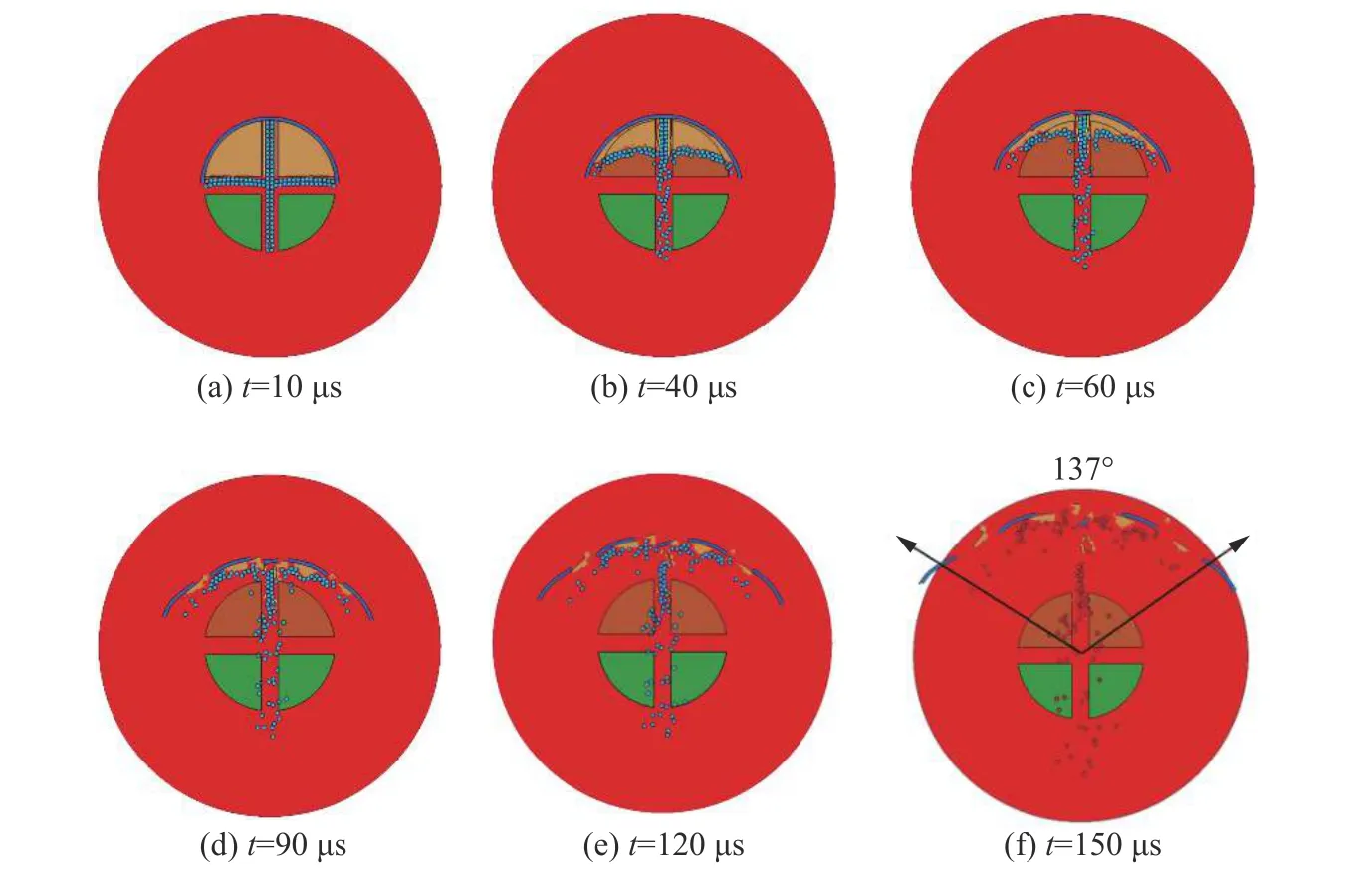
图5 相邻2 点起爆下破片径向飞散模拟结果Fig.5 Simulation results of fragment radial dispersion under adjacent two-point initiation

图6 相邻3 点起爆下破片径向飞散模拟结果Fig.6 Simulation results of fragment radial dispersion under adjacent three-point initiation

从图5～6 可以看出，两种起爆模式下破片的驱动过程大致分为3 个阶段：炸药爆轰冲击波加载阶段、产物膨胀加载及破片碰撞挤压阶段、破片稳定飞行阶段。在第1 阶段，当相邻2 块主装药或3 块主装药起爆后，爆轰波迅速向外传播，依次在聚氨酯、铝衬、破片及未起爆的分块装药中产生冲击波，此时破片由冲击波作用加速，并且铝衬、聚氨酯在冲击波作用下发生粉碎及飞散，由于冲击波加速过程很短，因此破片位移较小[14]。在第2 阶段，冲击波加载结束后，炸药爆轰产生的高温高压气体产物膨胀将进一步驱动破片，这个过程的持续时间比冲击波加载要长，可达到几十微秒[15]。在两者的共同作用下，破片获得较大的速度，且未起爆的分块装药一并被加速，由于装药密度远低于破片密度，因此粉碎的装药被爆轰产物先抛撒出去。同时，在破片加速过程中，由于破片呈双层相切排布，靠近炸药的内层破片速度高于外层破片，内外层破片会发生碰撞及挤压。对于∨字形内的破片，除内外层破片碰撞外，由于聚能效应，两处外层破片之间也存在碰撞现象。在第3 阶段，在150 µs 时刻破片加速过程结束，破片进入稳定飞行阶段，内外层破片以近似相同的速度向远处飞散。图7 给出了相邻2 点起爆、相邻3 点起爆时典型位置处的破片速度。

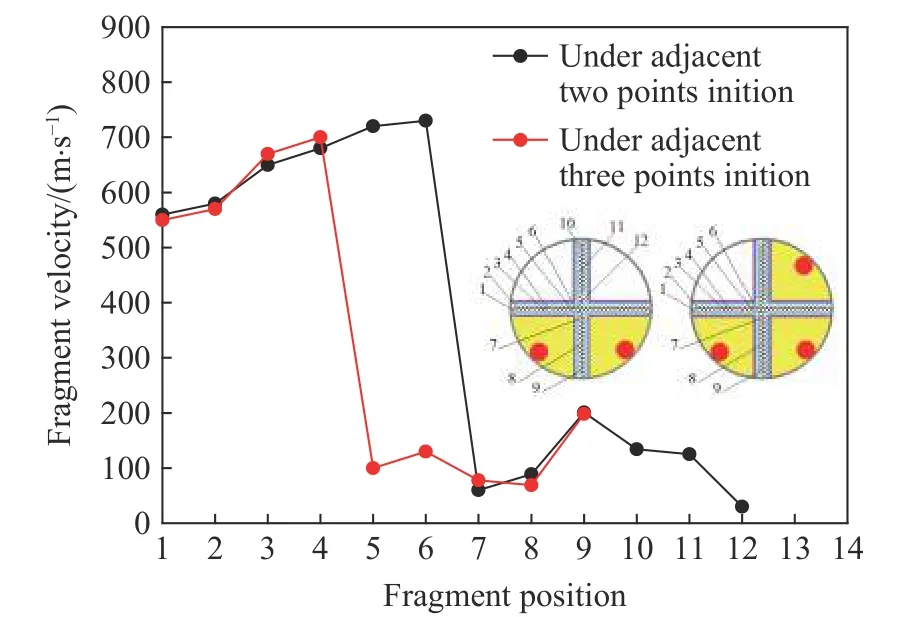
图7 典型位置处破片速度的模拟结果Fig.7 Simulation results of fragment velocity at typical locations

由图5、7 可知，对于相邻2 点起爆模式，一字形内破片在分块装药爆轰加载下飞散，且靠近战斗部中心点处速度最大（位置5～6 处，平均速度730.5 m/s），距离中心点越远稀疏波影响越显著，破片速度越低（位置1～2 处，平均速度560 m/s）；起爆的两处炸药之间的破片由于受到两侧炸药爆轰对称加载，作用力相互抵消，破片速度极低（位置7～9 处，速度70～198 m/s），未起爆的两处炸药之间的破片无对应的驱动炸药，致使破片速度极低（位置10～12 处，速度35～122 m/s）。因此，仅一字形内的高速破片可以实现对目标的定向杀伤，破片利用率达到50%，且破片径向飞散角度约为137°。

由图6～7 可知，对于相邻3 点起爆模式，∨字形内破片在分块炸药爆轰加载下飞散，破片速度呈现出明显的速度梯次分布特征。其中，靠近战斗部中心点处的速度极低（位置5～6 处，平均速度110 m/s），其余位置（位置1～4 处）处破片的速度与相邻2 点起爆结果基本一致，其中位置3～4 处的平均速度为700.2 m/s，位置1～2 处的平均速度为550 m/s，同样，起爆的分块炸药之间的破片速度（位置7～9 处，速度71～198 m/s）极低。因此，∨字形内的破片形成定向杀伤区，破片利用率达到50%，且径向飞散角度仅为61°，比相邻2 点起爆模式下破片的定向杀伤区更窄，低附带安全区更大。

3 实验验证

3.1 实验方案

为验证数值模拟结果的可行性，制备了2 发单元样弹，如图8 所示，分别用于开展相邻2 点起爆和相邻3 点起爆下破片的飞散特性实验。其中样弹1 装填的钨球数量为3 562，装药质量为0.406 kg，总质量为1.220 kg，采用2 个电雷管同时起爆相邻2 个分块装药，每个起爆点位于轴线50 mm 处（即战斗部长度的1/2 处）。样弹2 装填钨球数量为3 564，装药质量为0.403 kg，总质量为1.218 kg，采用3 个电雷管同时起爆相邻3 个分块装药，每个起爆点同样位于轴线50 mm 处。

图8 实验样弹Fig.8 Experimental samples

为研究破片定向飞散的特性，在威力半径R=1.5 m 处布设弧长L=4 m、高度H=1.25 m 的1.5 mm 厚Q235A 钢板。以靶板竖直中心线90°为基准，向左右两侧以等间距为130 mm（5°）的间隔均匀划线；以靶板水平中心线0°为基准，向上下两侧以等间距为55 mm（2°）的间隔均匀划线。径向拦截角度不小于150°，轴向拦截角度不小于44°。通过统计每个区域内的破片数，可得出两种不同起爆模式下破片径向分布的特性，靶场布局如图9 所示。同时，采用高速摄影对定向杀伤区破片撞击靶板的过程进行观测，拍摄频率为20 000 s-1，以获得破片的速度。

图9 实验布局Fig.9 Experimental layout

3.2 结果分析及讨论

3.2.1 破片飞散速度

利用图像处理软件[16]得到两种起爆模式下破片撞击钢板形成的火光，高速摄影典型照片如图10～11 所示。

图10 相邻2 点起爆下破片撞击钢板的高速摄影典型照片Fig.10 Typical pictures of fragments penetrating steel plate by high-speed photography under adjacent two-point initiation

图11 相邻3 点起爆下破片撞击钢板的高速摄影典型照片Fig.11 Typical pictures of fragments penetrating steel plate by high-speed photography under adjacent three-point initiation

由图10～11 可看出，两种起爆模式下破片撞击钢板首次出现火光的时刻均为2.0 ms，之后，火光区域由中心位置逐步向四周扩大。相邻2 点起爆模式下至2.8 ms 时刻火光区域不再扩大，相邻3 点起爆模式下至2.6 ms 时刻火光区域不再扩大，表明定向杀伤区内破片存在速度梯度。由于距离较近，取威力半径内破片平均速度作为破片初速，据此可求得两种起爆模式下破片的最大速度均为750 m/s，相邻2 点起爆模式下破片的最小速度为535 m/s，相邻3 点起爆模式下破片的最小速度为577 m/s。将实验结果与数值模拟结果进行比较并列于表5 中，可以看出最大速度和最小速度的实验值与数值模拟值基本一致，最大偏差为7.11%，表明利用数值模拟计算的破片速度是准确的。

表5 破片速度数值模拟结果与实验值对比Table 5 Comparison between numerical simulation results and test data on fragment velocity

3.2.2 破片径向飞散角

由于破片速度存在差异，因此破片对靶板毁伤的形式包括了穿孔和凹坑两种，如图12 所示。为合理分析破片径向飞散的特性，将所有着靶的破片数均统计在内，据此绘制的两种起爆方式下破片径向飞散的分布如图13 所示。

图12 破片对靶板毁伤形貌Fig.12 Damage appearance of steel plate by fragment

图13 两种起爆方式下破片径向分布的统计结果Fig.13 Statistical results of fragment radial distribution under two different initiation modes

由图13 可知，相邻2 点起爆模式下，定向区域内破片的径向飞散范围为15°～160°，即径向飞散角为145°，飞散角内破片的着靶数量为1 801，占破片总数的50.4%，非定向区域内破片的着靶数量为0；相邻3 点起爆模式下，定向区域内破片径向飞散的范围为50°～115°，即径向飞散角为65°，破片的着靶数量为1 547，占破片总数的43%，低于理论及模拟值（50%），主要原因是靠近战斗部中心点处破片的速度极低，未能在钢板上形成穿孔或明显凹坑，同样地，非定向区域内破片着靶数量为0。与数值模拟结果相比，相邻2 点起爆时破片径向飞散角的偏差为5.84%，相邻3 点起爆时破片径向飞散角的偏差为6.6%，表明利用数值模拟计算的破片径向飞散角是准确的。

进一步分析发现，两种起爆模式下，破片定向杀伤区内径向方向的破片均呈现出明显的正态分布特征，即越靠近靶板竖直中心线90°，破片数量越多，两侧破片数量逐渐减少。根据正态分布函数，正态分布中利用尺度参数б描述数据分布的离散程度，其值越大，数据分布越分散，其值越小，数据分布越集中。经过比较分析可知，相邻2 点起爆下，б值较小，破片数量分布相对分散；而相邻3 点起爆模式下，б值较大，曲线呈瘦高状。

对两种起爆模式下定向杀伤区内破片的穿甲率进行统计发现，相邻2 点起爆模式和相邻3 点起爆模式下，破片的穿孔数分别为1 701、1 309，穿甲率分别为94.4%、84.6%。出现这种明显差异的原因，是由于相邻2 点起爆下，一字形内破片速度差异较小，而∨字形内靠近战斗部中心点处的破片速度相对较低。

3.2.3 基于能量分配的速度公式

无论是相邻2 点起爆或是相邻3 点起爆，均假设各个分块装药之间不存在干扰，则可以取其中任一处分块装药作为建立求解破片速度的计算模型。利用微元思想，基于速度是破片到起爆点距离的函数，建立偏心定向一点起爆时能量分配模型[17-18]，每个破片的动能来自于能量分配角度θ 所夹的装药爆轰释放的能量。将破片初速表示为起爆点I与破片切点的连线和起爆点与装药质心O的连线的夹角δ 以及θ 的函数关系，据此可求得不同位置处破片的速度，进而得到偏心单点起爆下破片速度的分布规律。计算模型如图14 所示。

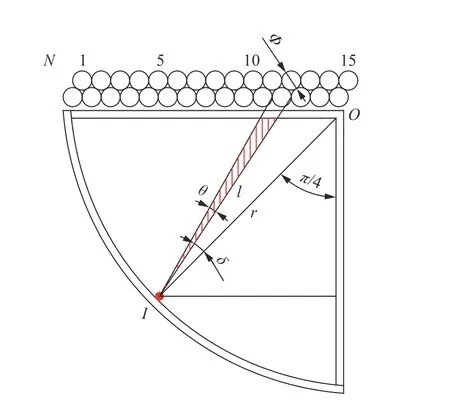
图14 破片速度的计算模型Fig.14 Calculation model of fragment velocity

在建立计算模型之前，作如下假设：

（1）分块装药近似为1/4 圆形；

（2）炸药的化学能完全转化成产物气体的动能和破片的动能，忽略内衬和聚氨酯的动能，以及壳体膨胀和破碎能；

（3）内外层破片速度相等，不存在速度梯度差，即将内外层破片看作一个整体；

（4）忽略侧向及反应区后产生的稀疏波的影响；

（5）产物气体的速度沿周向分布是线性的；

（6）炸药爆轰后，产物气体均匀膨胀，且各处的密度相等。

首先计算出能量分配角度对应的装药长度l：

式中：r为分块装药半径。

则各个位置处破片对应的装药质量ΔM：

式中：Φ 为破片直径，ρe为装药密度。

不同位置处破片对应的未反应炸药质量m'为:

式中：N为破片编号，本文中取值为1～15。

由式（5）～（6）求得对应的局部装填比β 为：

式中：m为单枚破片的质量。

根据一个平板金属与一个平板装药相贴合近似推导得出的破片初速计算公式[19]为：

联立式（4）～（8）可以计算得到破片1～15 的理论速度。同时，由于数值模拟计算的破片速度与实验值很接近，因此，为便于与理论值进行比较，对所有破片速度进行了模拟计算。此处模拟值为内外层破片速度的平均值，模拟值与理论值的对比结果如图15 所示。

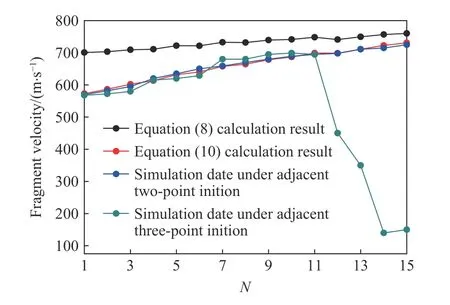
图15 破片速度理论计算值与数值模拟值比较Fig.15 Comparison between the theoretical calculation results and numerical simulation data

从图15 可以看出，根据式（8）计算的理论速度大于数值模拟结果，且破片编号越小，差值越大。需要说明的是，此处不计入相邻3 点起爆下由于破片碰撞影响的破片12～15。因此，需要对式（8）作进一步修正。根据不同位置处破片速度差值的变化分析，采用修正系数fx：

式中：a、b为系数，x为不同位置处破片对应的距离，且越靠近点O，其值越大。

由非线性拟合可得a=0.214 18，b=-1.150 43，则修正后不同位置处破片速度的计算公式为：

由图15 可以看出，利用式（10）求得的破片速度与模拟值基本吻合，其最大偏差不超过4.2%，而对于相邻3 点起爆下破片12～15 的速度的理论计算模型需要进一步分析。

4 结 论

设计了一种十字形内置破片定向战斗部，相较于传统破片外置及破片芯式战斗部，十字形内置破片定向战斗部具有破片速度高、定向区破片利用率大的特点。采用数值模拟及实验对战斗部破片飞散速度及径向飞散特性进行了研究，并建立了破片速度理论模型，得到以下主要结论。

(1)根据目标方位，定向战斗部包括两种作用模式：一是相邻2 点起爆，一字形内破片定向飞散毁伤目标；二是相邻3 点起爆，∨字形内破片定向飞散毁伤目标。其余区域内破片无杀伤能力，呈现出低附带毁伤效果。

(2)两种起爆模式下，定向杀伤区破片利用率均达到50%。相邻2 点起爆模式下，定向杀伤区破片径向飞散角不超过145°，破片速度535～750 m/s，对1.5 mm Q235 钢板穿甲率94.4%；相邻3 点起爆模式下，定向杀伤区破片径向飞散角相对更窄，不超过65°，破片速度577 ～750 m/s，对1.5 mm Q235 钢板穿甲率84.6%。其余区域内破片速度极低，不具备杀伤能力。

(3)基于能量分配模型建立的破片速度公式准确性较高，其相对于数值模拟结果最大偏差不超过4.2%。