隧道衬砌病害对结构安全性影响机理研究

杨朝帅,崔 臻,牛富生,王百泉

(1.中铁隧道局集团有限公司,广东 广州 511458;2.广东省隧道结构智能监控与维护企业重点实验室,广东 广州 511458;3.中铁隧道勘察设计研究院有限公司,广东 广州 511458;4.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室,湖北 武汉 430071)

隧道工程技术发展对完善国家交通体系、发展国民经济有重大作用。截至目前,随着我国隧道工程向埋深更深、距离更长、断面更大的方向发展,面临的地质环境也越来越复杂,目前的施工技术难度、装备与材料的适用性也面临巨大挑战[1-3]。随着各国隧道建设的迅猛发展,隧道病害问题作为世界性难题日益突出。据统计,已运营隧道普遍存在各种形式的结构病害,如衬砌开裂、渗漏水、大变形、衬砌背后脱空、钢筋锈蚀等,这些病害问题对隧道安全运营是一种潜在的隐患[4-6]。因此,未来很长一段时间内,我国的隧道工程技术的发展将由以往的大规模建设向今后的病害治理修复转变[7-8]。因此,对隧道工程结构的开裂、渗漏水、背后脱空等健康状况进行分析和量化评价,具有一定的研究意义。

目前,很多国家都建立了隧道健康状态评价体系,但这些评价体系更多是定性判断,定量化健康评价较少[9-10]。另外,在隧道健康状态方面,对很多工程进行了病害数据的现场测试,但数据的离散性较大,应用范围较窄,同时与实测数据对应的隧道病害安全影响机理不明确,因此当前的隧道健康状态评价体系具有一定的局限性。为了评价隧道病害对结构安全的影响机制,杨惠林[11]结合祁家大山隧道病害检测数据,建立了数值计算模型,分析了衬砌结构承载力的损失程度,并提出了合理的病害治理方案;王勇[12]利用有限元计算软件,研究了平面状态隧道开挖支护过程中不同衬砌厚度工况下的围岩荷载,并对二次衬砌混凝土结构的承载力进行了校核。聂智平等[13]根据某隧道漏水和裂缝的调查结果,基于荷载-结构方法建立隧道衬砌的数值模型,并对最薄弱段的承载力进行力学分析。刘庭金等[14]采用荷载-结构法,通过监测隧道衬砌压力校核衬砌压力,确定了衬砌结构的稳定性。刘永华[15]采用荷载-结构法建立隧道拱部衬砌背后空洞、衬砌截面厚度、衬砌开裂等病害模型,并结合实测数据验证了模型的准确性。对于隧道衬砌结构开裂病害,张玉军等[16]认为裂缝深度因素对结构稳定性影响较大,而裂缝宽度对结构的稳定性影响较小。

综上所述,对隧道病害相关研究主要是集中在结构稳定性安全方面,包括数值模拟和病害检测监测等,但以往的研究模型未考虑病害的影响机理,因此模型的可靠性不高,计算误差也较大。因此,如何建立包含病害影响机理的数值模型,对研究成果可靠性至关重要。本文建立地层-结构计算模型,引入了复合衬砌隧道安全系数的计算方法,在此基础上分别讨论衬砌背后空洞、衬砌开裂、渗水这三种典型病害的作用机理及影响规律,对结构安全系数与病害特征指标的敏感性进行分析,以期研究隧道衬砌开裂、渗水、衬砌背后空洞三种典型病害的作用机理与影响规律,剖析病害对结构安全的影响程度和影响范围。

1 隧道衬砌病害的模拟原理

1.1 分析模型

本研究中采用国标《工程岩体分类标准》(GB/T 50218—2014)推荐的岩体力学参数,分别见表1、表2。

表1 分析用的岩体力学参数

表2 复合衬砌支护设计参数

当考虑二维分析计算时,在Phase2 V8.0 软件中分别建立Ⅲ、Ⅳ、Ⅴ类围岩中双线隧道的典型模型,其中数值模型尺寸取大于三倍洞径,竖直向与水平向尺寸均为100 m,模型四周均取为三向约束边界。见图1。分别考虑Ⅲ、Ⅳ、Ⅴ类围岩条件下的典型喷锚复合衬砌支护,支护结构的支护时机考虑为围岩荷载释放率为80%时。模拟过程具体如下:

图1 Ⅳ类围岩双线隧道计算模型

(1) 确定整个模型的区域和边界;(2) 设置围岩地层参数;(3) 根据隧道开挖影响范围细分有限元网格,并定义初始地应力;(4) 添加初期支护结构单元,同时释放部分围岩应力;(5) 添加二次衬砌结构单元;(6) 计算至收敛。

1.2 隧道开挖响应

图2给出了在当前围岩力学参数条件下,隧道开挖完成后变形云图,可见,隧道最大开挖变形为0.005 m,发生在隧道仰拱部位;隧道顶拱的沉降变形约为0.004 m。图3给出了III类围岩条件下,隧道开挖完成后衬砌结构的轴力、弯矩、剪力图,可见衬砌结构内力以轴力为主,弯矩与剪力量值均较小,最大轴力量值约为1.28 MN,发生在左右边墙拱脚部位。

图3 隧道开挖支护完成后衬砌内力图

1.3 隧道安全系数计算方法

如上节所示,在计算衬砌结构时,获取的结果为衬砌上的弯矩、剪力和轴力这三种内力成果。当需要用这三种内力成果对衬砌进行承载力校核时,比较方便和直观的办法是利用承载力包络线图[17]。当衬砌材料受力状态点位于承载力包络线以内,认为衬砌结构是安全的;一旦衬砌材料受力状态点位于承载力包络线以外,则认为衬砌结构开裂破坏。

(1) 弯矩-轴力(M-N)安全系数

根据弹性梁理论,有弯矩、轴力与衬砌材料极限正应力关系如下:

(1)

同时约定安全系数定义:

(2)

则通过以上二式可以得到压缩破坏时的轴力:

(3)

拉伸破坏时的轴力:

(4)

极限弯矩:

(5)

式中:Fs为安全系数,在本报告中采用Fs=1;t为二次衬砌厚度;A为衬砌结构的截面面积;I为衬砌结构惯性矩;σc和σt分别为衬砌结构混凝土的抗拉强度和抗压强度。

(2) 剪力-轴力(Q-N)安全系数

在深梁理论中,剪力Q作用下,梁中最大剪应力出现在中性轴部位,且量值约如下:

(6)

假定在最大剪应力和最大正应力条件下,梁中平面上应力状态如下式:

(7)

同时约定安全系数定义:

(8)

则通过以上三式可以得到压缩破坏时的轴力:

(9)

拉伸破坏时的轴力:

(10)

极限剪力:

(11)

根据以上公式,即可分别求得混凝土衬砌的M-N图与Q-N图,根据两图即可得到衬砌结构的安全系数,隧道的最小安全系数取两图中的较小值即可。

1.4 隧道衬砌结构病害的模拟

1.4.1 隧道衬砌开裂的模拟

在本研究中,为了考虑隧道结构不同部位开裂对结构安全的影响机理,分别考虑了顶拱、边墙、仰拱三个部位的开裂情况。

在对裂缝进行模拟时,为了简化起见,将裂缝简化为圆弧形,如图4。即假设开裂部位产生一个半径为R的凹坑,进一步将该开裂部位简化为一个宽度为2R,深度为R的矩形缺陷,如此实现衬砌开裂在数值软件中的模拟。

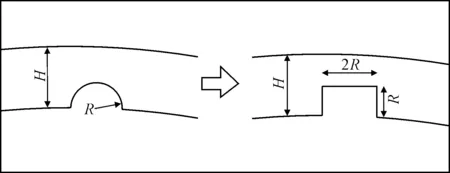
图4 衬砌结构开裂部位的模拟原理

1.4.2 隧道衬砌渗水的模拟

当需要模拟隧道衬砌隧道渗水的危害时,将基于水-力耦合数值模拟,采用无渗流模式模拟静水压作用下隧道衬砌的渗水,在这种模式下,可在节点上设置孔隙水压力,只是孔隙水压是保持不变的,岩土体的屈服判断由有效应力决定。

在设置渗水裂缝时,采用了与上一段中相同的裂缝模拟方法与设置部位。

1.4.3 隧道衬砌后空洞的模拟

在对裂缝进行模拟时,为了简化起见,将裂缝简化为岩体中的圆弧形空洞,如图5,并直接在数值软件中对空洞进行模拟。对于空洞的部位,也采取与上一段中相同的设置部位。

图5 衬砌后空洞的模拟

2 衬砌开裂对隧道安全性的影响

图6(a)、图6(b)给出了Ⅲ类围岩条件下,顶拱位置开裂,开裂深度R/H=0.5的条件下,衬砌的M-N安全系数、Q-N安全系数,可见衬砌开裂对衬砌安全系数具有不利影响。进一步,图6(c)为Ⅲ类围岩条件下,开裂深度R/H=0.5的条件下,顶拱位置下衬砌的最小安全系数。当考虑衬砌开裂之后,顶拱部位安全系数为最低,约4.6左右,仍满足最小为2的规范要求。

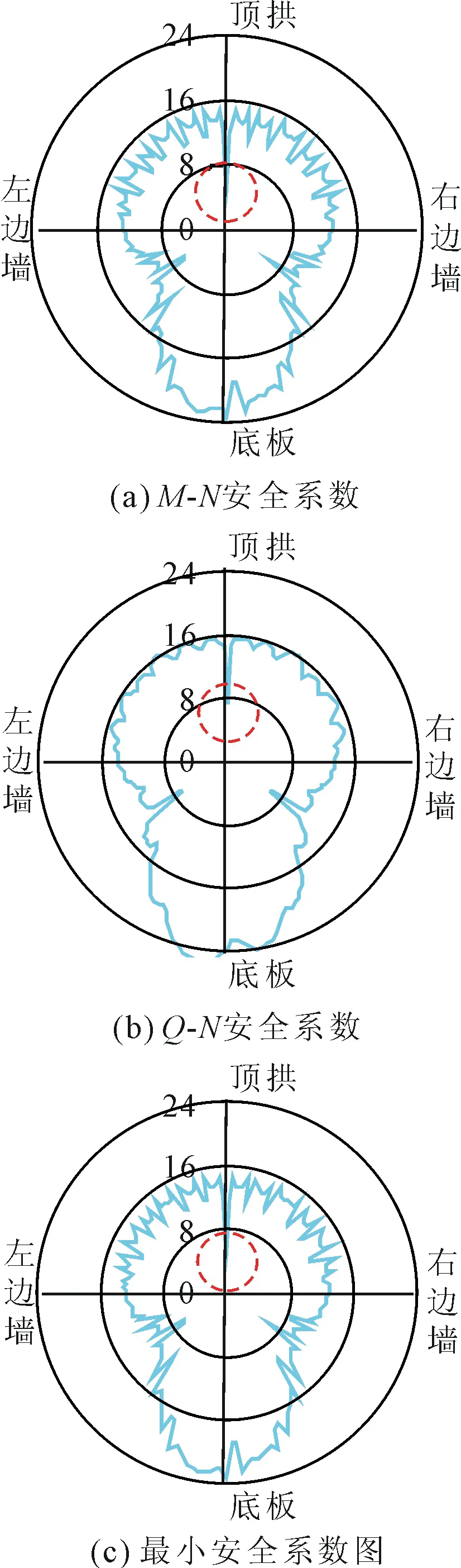
图6 顶拱部位开裂后衬砌安全系数图

图7给出了Ⅲ类围岩下,衬砌无裂缝与顶拱出现裂缝时,衬砌的最小安全系数对比。可见,裂缝仅影响局部衬砌的安全系数,对衬砌整体安全程度影响不大。因此,当考虑衬砌开裂之后,顶拱部位安全系数为最低,约4.6左右,仍满足最小为2的规范要求。

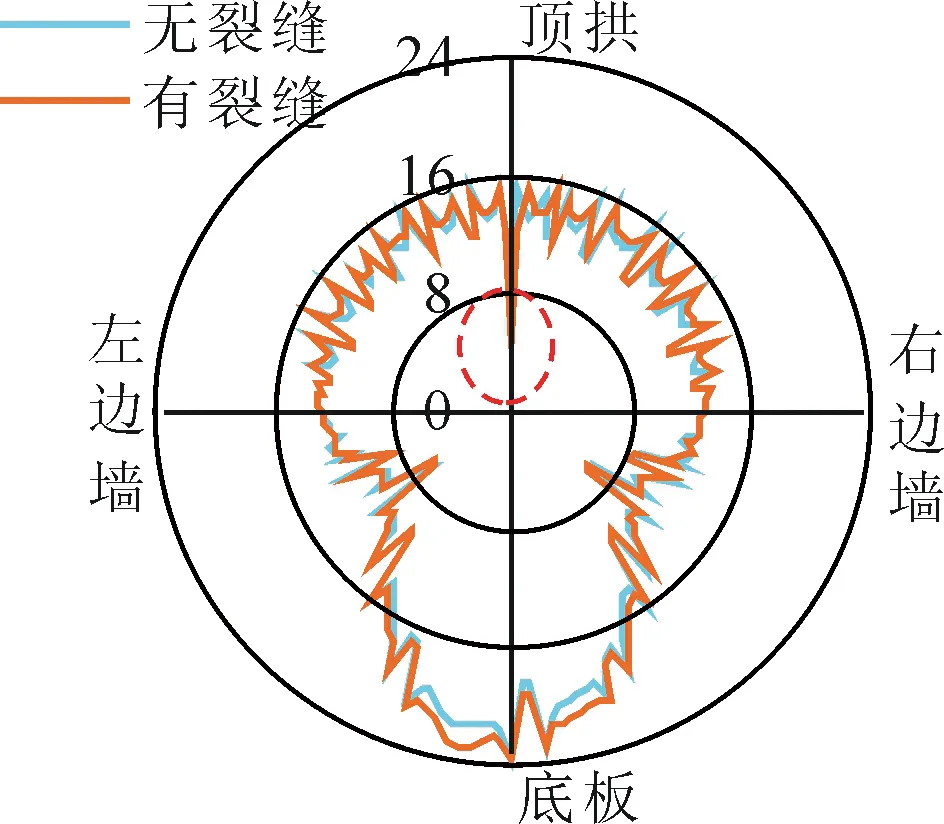
图7 顶拱有/无开裂时衬砌最小安全系数图

图8给出了Ⅲ类围岩条件下裂缝位置对衬砌安全系数的影响。可见,仰拱部位安全系数降低最多,但由于顶拱部位安全系数原本量值较小,因此最终顶拱部位安全系数最低,约为4.6左右。

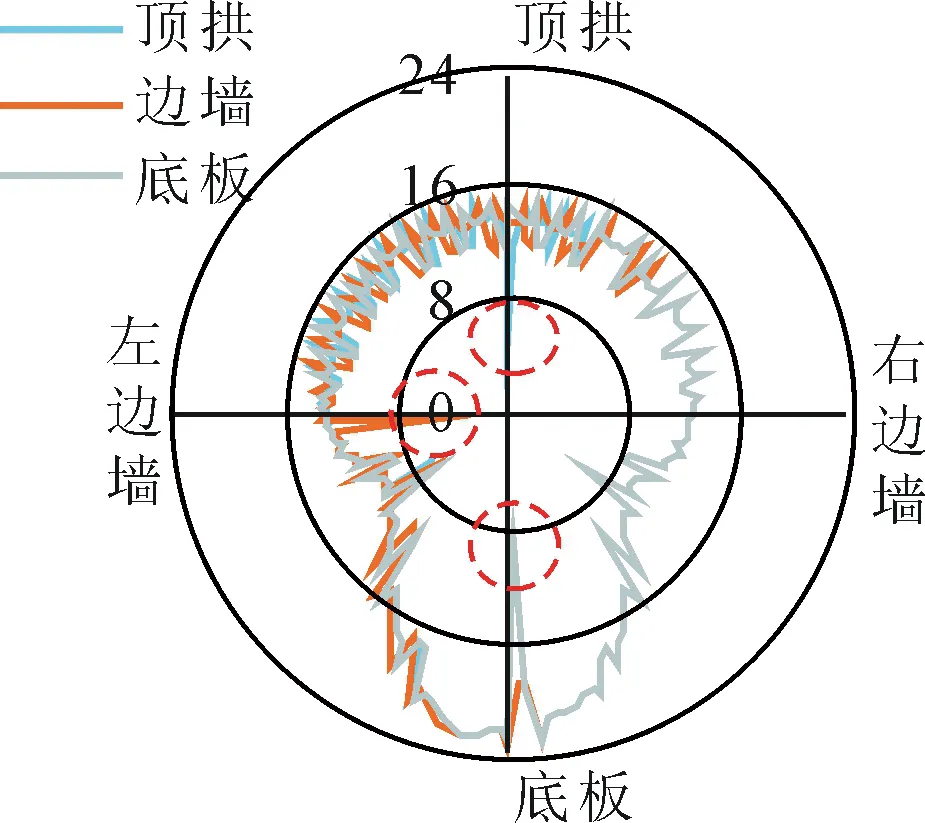
图8 裂缝位置对衬砌最小安全系数的影响

图9给出了Ⅲ类围岩条件下,开裂深度R/H=0.3、0.5、0.7条件下,顶拱部位开裂后衬砌的安全系数。可见,随着开裂深度的增加,安全系数逐渐减小。为了更加表达清楚,进一步的,图10为衬砌顶拱最小安全系数。当开裂深度从0.3增加到0.7倍衬砌厚度时,最小安全系数由7.3降低到2.24。

图9 裂缝深度对衬砌最小安全系数的影响

图10 裂缝深度对衬砌顶拱最小安全系数的影响

图11给出了在Ⅲ类围岩条件下,不同的裂缝数量对衬砌安全系数的影响。可见,裂缝仅影响局部衬砌的安全系数,对衬砌整体安全程度影响不大。因此,当考虑衬砌开裂之后,顶拱部位安全系数为最低,约4.6左右,仍满足最小为2的规范要求。

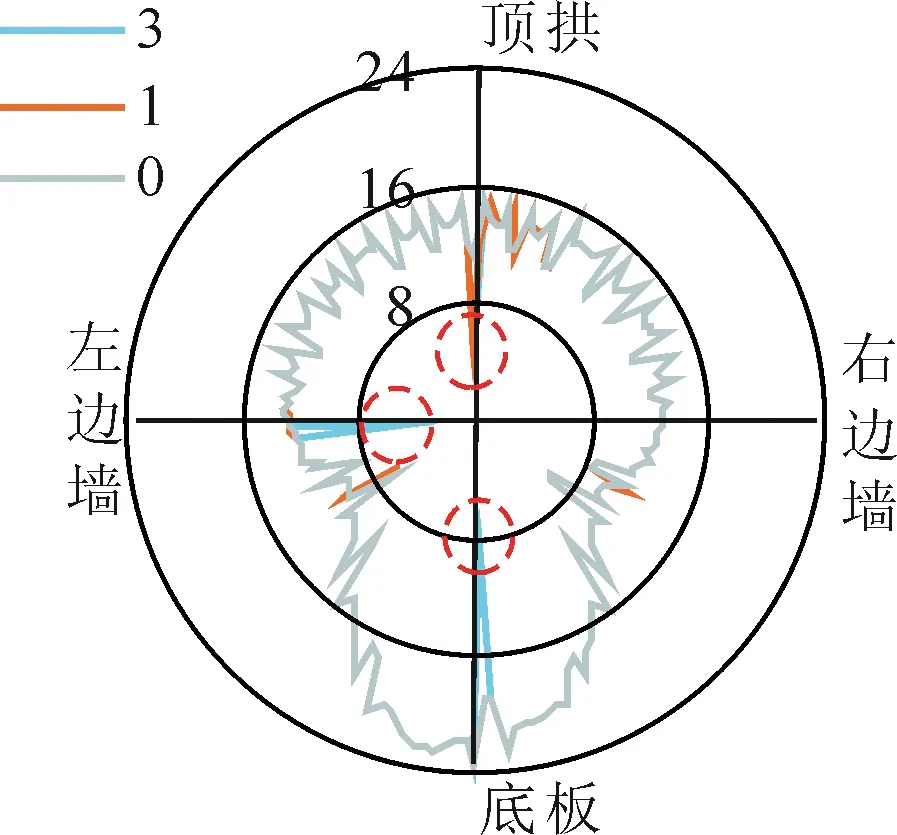
图11 裂缝数量对衬砌最小安全系数的影响

3 隧道渗水对隧道安全性的影响

图12给出了Ⅲ类围岩条件下,开裂深度R/H=0.5、水头40 m的条件下,隧道顶拱开裂渗水与否对衬砌最小安全系数的影响。可见,考虑水压时,隧道衬砌整体安全系数均不同程度减小,顶拱部位减小程度最大,由不考虑渗水时的4.6左右,降低到3.96左右。

图12 衬砌顶拱渗水与否对衬砌最小安全系数的影响

图13给出了III类围岩条件下开裂渗水位置对衬砌安全系数的影响。可见,不同部位开裂渗水对衬砌安全系数的影响均局限在较小的范围内,其中的仰拱部位安全系数降低最多,但由于顶拱部位安全系数原本量值较小,因此最终顶拱部位安全系数最低,约为3.96左右。

图14给出了III类围岩条件下不同水头时衬砌最小安全系数分布情况,考虑的开裂渗水部位为顶拱,可见水压对衬砌安全系数整体都有降低,当水头从30 m增加到50 m的时候,最小安全系数减小了0.6左右。

图14 衬砌渗水水头对衬砌最小安全系数的影响

4 衬砌后空洞对隧道安全性的影响

图15给出了Ⅲ类围岩条件,空洞半径0.5 m条件下隧道有无衬砌后空洞对衬砌最小安全系数的影响。可见衬砌后空洞对衬砌安全状态影响范围较大,在空洞范围内的衬砌安全系数受到不利影响,在空洞范围外的衬砌安全系数有所提高。当考虑空洞后,顶拱衬砌安全系数从11.0降低到3.9左右。

图15 衬砌后有无空洞对衬砌最小安全系数的影响

图16给出了Ⅲ类围岩条件下,空洞半径0.5 m条件下,不同空洞位置下衬砌最小安全系数,可见不同部位的衬砌开裂均对衬砌安全系数具有不利影响。其中,顶拱、仰拱部位安全系数降低最为明显。由于顶拱部位总体安全系数比仰拱部位小,因此,当考虑衬砌开裂之后,顶拱部位安全系数为最低,约3.9左右,仍满足最小为2的规范要求。

图16 衬砌后空洞位置对衬砌最小安全系数的影响

图17给出了Ⅲ类围岩条件下,空洞半径R=0.25 m、0.5 m、1 m条件下,顶拱部位开裂后下衬砌的最小安全系数。可见,随着空洞深度的增加,安全系数逐渐减小。如图18可见,当空洞半径从0.25 m增加到1 m的时候,衬砌顶拱最小安全系数由6.3降低到2.2。

图17 衬砌后空洞尺寸对衬砌最小安全系数的影响

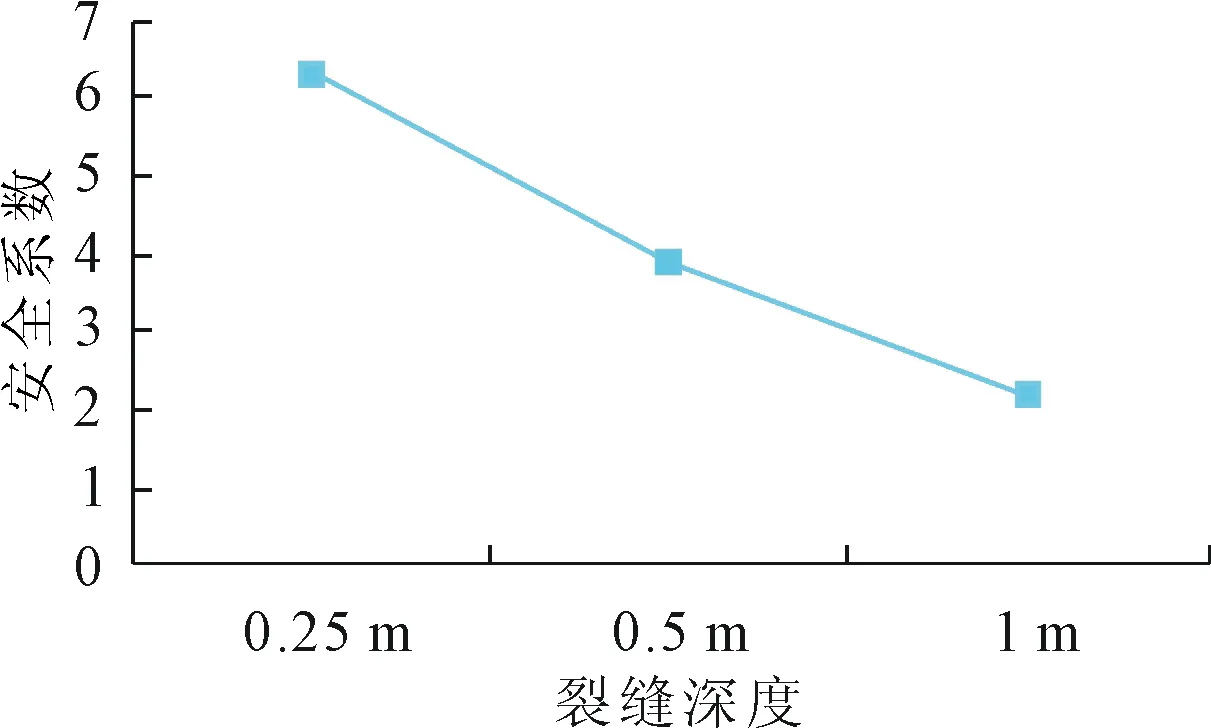
图18 衬砌后空洞尺寸对衬砌顶拱最小安全系数的影响

5 结 论

(1) 衬砌开裂时仰拱部位安全系数降低最多,但由于顶拱部位安全系数原本量值较小,因此最终顶拱部位安全系数最低,约为4.6左右;当开裂深度从0.3增加到0.7倍衬砌厚度的时候,最小安全系数由7.3降低到2.24;对于不同的裂缝数量对衬砌安全系数的影响而言,裂缝仅影响局部衬砌的安全系数,对衬砌整体安全程度影响不大。

(2) 考虑渗水时,仰拱部位安全系数降低仍然最多,但由于顶拱部位安全系数原本量值较小,因此最终顶拱部位安全系数最低,约为3.96左右,小于不考虑渗水时的4.6左右;当水头从30 m增加到50 m的时候,最小安全系数减小了0.6左右。

(3) 考虑衬砌后空洞时,顶拱、仰拱部位安全系数降低最为明显,仰拱部位安全系数降低最多,但由于顶拱部位安全系数原本量值较小,因此最终顶拱部位安全系数最低,约为3.9左右;空洞尺寸对衬砌安全系数影响显著,当空洞半径从0.25 m增加到1 m的时候,最小安全系数由6.3降低到2.2。

本研究尚存在的不足:由于隧道病害特征形式复杂、不确定性较强,因此通过数据模拟对病害进行规则化建模,有一定的误差,但不影响对计算结果规律的分析,不同病害之间的相互影响还需要今后更深入的研究。