基于流固耦合的深基坑周边地表沉降界线分析

李 明,李化明

(佳木斯大学 建筑工程学院, 黑龙江 佳木斯 154007)

近些年,深基坑工程在人口相对密集区域出现的频率逐渐增加,并向着“更大、更宽、更深”的趋势发展[1]。伴随基坑各方向尺寸的增加,工程施工引起的周边地表沉降也在逐渐增大,这直接影响到了临近既有建(构)筑物或地下管线的正常使用。因此,研究如何减小工程施工所引起的周边土体沉降一直倍受学者关注。

赵殿鹏等[2]运用有限元软件对某一实际基坑进行模拟,结果表明:放坡开挖结合桩支护的基坑支护方案具有较好的变形控制效果。李光明等[3]通过抽象化数学模型分析了止水帷幕深度、滤水管插入深度及降水速率对基坑变形的控制效果。张俊杰等[4]运用有限元软件midas GTS NX对沈阳龙门地铁车站基坑进行了模拟分析,结果表明:适度的增加围护桩嵌固深度与合理的布置支撑架设的位置均可起到一定的变形控制效果。俞强[5]通过对福州某一基坑工程进行实地监测,提出优化围护结构刚度与支撑体系等措施控制基坑变形。莫品强等[6]通过计算模型,提出了通过优化冠梁和支撑的截面参数与位置来控制基坑变形。孙铁军等[7]通过对某一基坑工程进行数据监测,提出采用井点降水措施控制基坑边坡变形。刘志刚[8]通过对上海市某一实际地铁车站基坑进行布点监测,提出通过严格遵循时空效应原理或采用合理的开挖方式来控制基坑工程变形。郑刚等[9]以某邻近地铁结构的大面积基坑工程为实例,通过监测数据分析了注浆对土体变形的控制效果。王雄等[10]运用PLAXIS 3D对一地铁车站基坑进行开挖模拟,分析了冻结法施工对基坑周边土体的变形控制效果。朱晓波[11]通过对上海市某一基坑项目进行数据监测,分析了分层、垂直开挖的基坑变形控制效果。

施成华等[12]对一实际基坑工程进行理论分析,结果表明:在距基坑周边一定范围以内,开挖和降水引所导致的地表变形大致相同,而在距基坑较远处,地表变形主要由降水导致。Roberts[13]通过对一实际基坑工程监测数据进行分析,得出基坑外一定范围内的沉降是由应力场的改变而引起的,而范围外的沉降主要是由渗流场的改变所引起。朱雁飞[14]通过有限元软件ABAQUS对一实际基坑工程进行降水开挖模拟,模拟结果表明:在距离基坑一倍开挖深度的范围内,回灌井点对基坑外土体沉降几乎没有影响。张明飞[15]运用有限差分软件FLAC3D对实际工程进行模拟分析,提出坑外两倍开挖深度外的地表沉降主要由降水引起。张宏洲等[16]进行了模拟回灌实验,实验结果表明:近基坑侧回灌井的回灌效果略差于远基坑侧回灌井。

综上所述,已有相对较多的学者分别提出了针对于基坑开挖或基坑降水所导致的基坑周边沉降变形控制措施,但却较少关注被保护对象是否处在基坑开挖或基坑降水所主导的沉降变形区域内。若被保护建(构)筑物位于被基坑降水所主导的区域,却采取了针对于基坑开挖的沉降控制措施,那么控制变形的效果与经济效益势必不好,反之同理。目前,已有少部分学者对基坑外地表沉降主导分区进行了初步探索,但却并没有真正的触及到问题核心,更没有提出“基坑周边地表沉降主导界线”的概念。

本文运用有限元软件midas GTS NX,在考虑流固耦合的先决条件下,对基坑周边地表沉降区域是否存在界线问题进行分析。使得设计人员能够依据被保护建(构)筑物所在的区域,制定出相对较为高效与合理的变形控制方案,具有一定的现实指导意义。

1 工程背景

1.1 工程概况

本工程位于广州市某交十字叉路口的东南角,北面与西面均面向公路,工程周边环境较为复杂,变形控制要求相对较高。现场施工场地存在矩形二层地下室,长53 m,宽为49 m,总开挖深度12.4 m。

1.2 工程地质与水文地质条件

依据本工程的地质勘察报告,场地土层物理性质见表1。

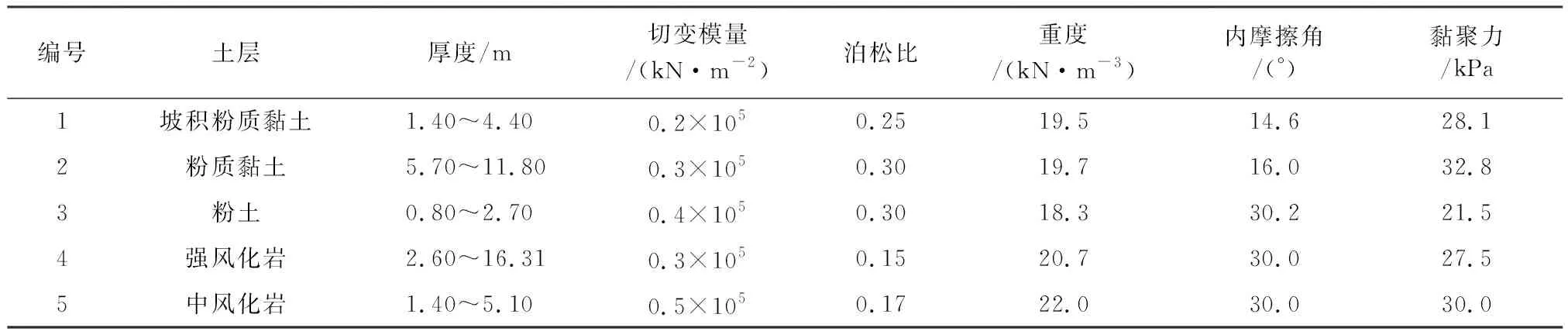
表1 场地土层物理参数

在场地地下水中,水位埋深为1.28 m～2.77 m,大气降水为其主要供应来源。场地中的粉质黏土与粉土土层透水性相对较差。

1.3 基坑支护方案

基坑围护体系采用地下连续墙与混凝土内支撑围护体系,地下连续墙厚为750 mm,深度为20 m。共两道内支撑,对撑平面尺寸为750 mm×1 000 mm,角撑与斜撑平面尺寸为600 mm×700 mm,两道支撑中心线标高分别为-3.6 m,-8.7 m。共设立四根立柱,直径为1 m。基坑支护结构剖面图见图1。

图1 基坑支护剖面图

1.4 降水方案

坑内井点降水、坑外不降水。采用分步,分层降水。共分三次,降深分别为-5 m,-10.2 m,-13.4 m。基坑总涌水量为630 m3/d,共32口井,沿基坑内侧布置,间距为6 m。

1.5 土方开挖方案

该基坑工程共进行三步开挖,依次开挖至地表下4.1 m、9.2 m与12.4 m处,并在第一、二步开挖结束后,进行第一道与第二道混凝土支撑的架设。

1.6 变形监测方案

地连墙墙身水平位移监测:采用伺服加速器计式测斜仪测量地连墙的水平位移,采用测斜管进行测量。监测频率为1次/d。

地表沉降监测:所设立的测点尽可能的贯穿路面的表面,设置在强度较高的土体中。监测频率为1次/d。

2 有限元模型

2.1 模型尺寸与网格划分

运用有限元软件midas GTS NX建立三维基坑模型如图2所示。依据以往的建模经验[17],选取基坑施工水平方向的影响范围为3H～4H(H为基坑开挖深度),竖直方向为2H～4H,故确定本模型的尺寸为140 m×140 m×45 m(长×宽×高)。采用三维网格模拟土体,二维网格模拟基坑地连墙,一维网格模拟内支撑与基坑立柱。为尽可能的兼顾数值模型的计算效率与精确性,确定基坑部分的网格尺寸为2 m[17],外围土层的网格尺寸为3 m。

图2 有限元计算模型

2.2 计算本构与边界条件

首先是土层的本构选取,由土的压缩-回弹实验可知,土体在压缩固结时所表现出的变形含有塑性变形,同时在渗透力的作用下,土体的变形也将体现一定的塑性[18],故选择弹塑性本构。

midas GTS NX中的摩尔库伦计算模型与修正摩尔库仑计算模型均为弹塑性本构计算模型,由于摩尔库伦本构的土体只有单一刚度,不能处理土体卸荷时所表现出的变形特性[19],故选择修正摩尔库仑本构模型。其余各构件均为弹性本构模型。

模型计算类型选择应力-渗流-边坡(考虑渗流场与应力场单向耦合),模型四周设置x与y方向的位移约束边界条件,底部设置x、y及z方向的位移约束边界条件,顶部为自由边界[20]。

定义地表以下2.5 m均为潜水,同时,定义不同降水后的水位,借助界面功能析取止水帷幕。通过反复的激活与钝化不同深度位置的水头边界条件,来模拟基坑降水。

2.3 模型参数

各土体模型参数详见表1,围护体系参数见表2。

表2 围护结构参数

2.4 模拟结果验证

2.4.1 基坑周边地表沉降对比

基坑周边地表沉降的模拟值与监测值对比图如图3所示。由图3可知,模拟数据与监测数据的沉降分布规律大体相同,随着与基坑边缘距离的逐渐增加,均呈现出先增大后减小并逐渐趋于稳定的变化规律,且均于距边缘约一半开挖深度处达到峰值。整体分析,两组数据的地表沉降平均差值为0.036 mm,约为5.46%。

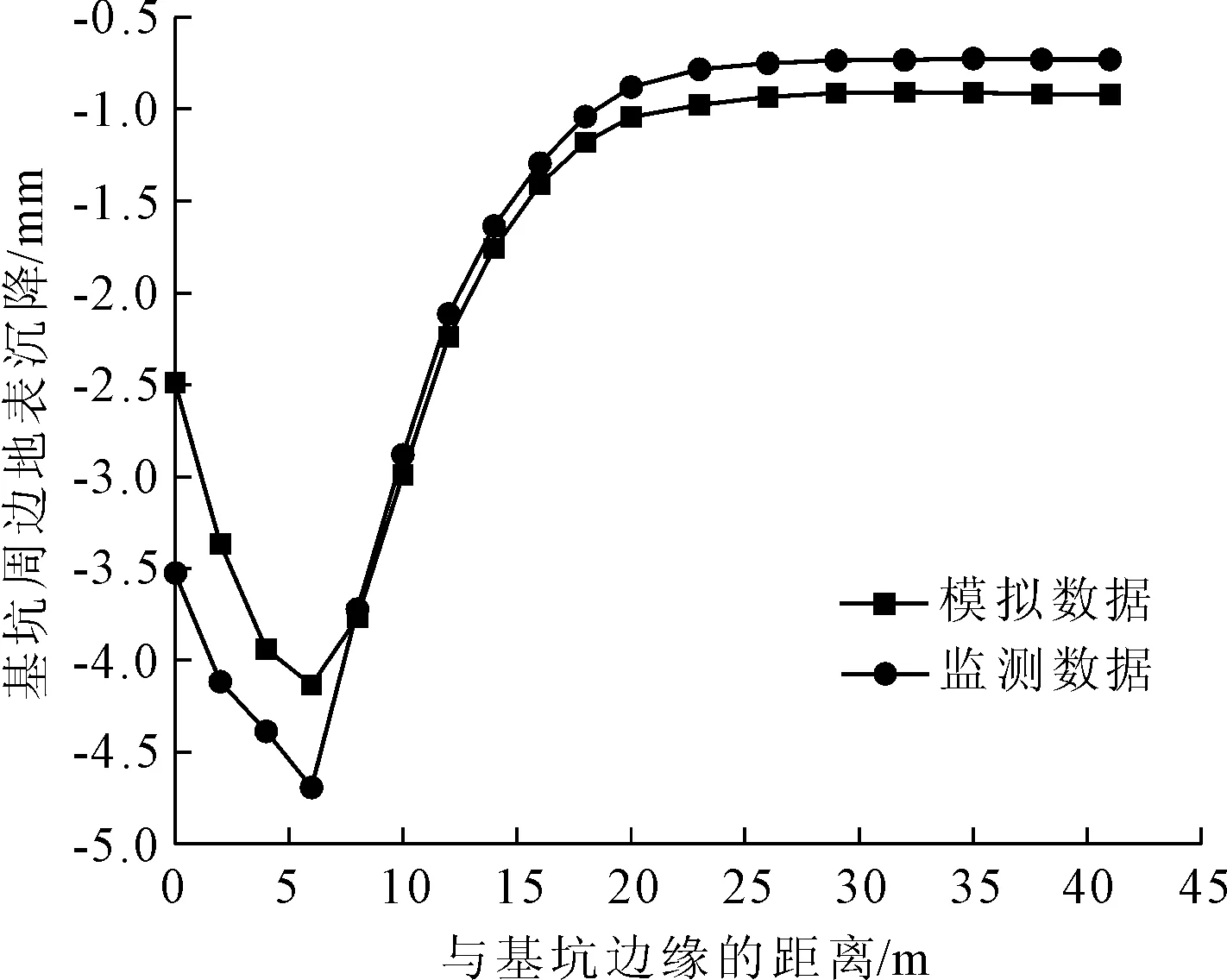
图3 地表沉降对比图

2.4.2 地连墙位移对比

地连墙水平位移的模拟数据与监测数据对比图如图4所示。由图4可知,模拟数据与监测数据所呈现出的位移分布规律基本相同,均呈现出随着深度的增加先增大后减小。模拟数据于深度约8.7 m处达到最大值,约为5.16 mm。监测数据于深度约6.8 m处达到最大值,约为5.06 mm。整体分析,两组数据的地连墙水平位移平均差值为0.39 mm,约为6.22%。

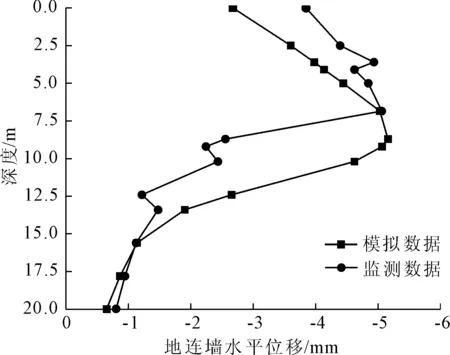
图4 地连墙水平位移对比图

2.5 模拟方案

为探究在考虑流固耦合的情况下,基坑周边地表沉降区是否存在沉降主导分界线的问题,共建立3个对比分析模型,分别为仅考虑土体开挖作用的基坑模型(模型一)、仅考虑降水作用(进行耦合计算)的基坑模型(模型二)及开挖与降水同时考虑的基坑模型(模型三)。

3 模拟结果分析

提取基坑模型较长侧外中部一直线上各节点的地表沉降数据进行分析。为更加充分地论述所研究的问题,分别对每一步基坑开挖或基坑降水后的地表沉降数据进行对比分析。

3.1 第一步开挖后的地表沉降数据分析

各模型第一步开挖或降水后的地表沉降对比图如图5所示。由图5可知,模型一与模型三的沉降分布规律基本相同,随着与基坑边缘距离的逐渐增加(各模型的节点间距均约为2.41 m),均呈现出先隆起后减小并逐渐趋于稳定的变化规律,且均于距基坑边缘约6 m处达到隆起位移的最大值。模型二的地表沉降分布形式较为单一,呈现为典型的“漏斗”状,既随着与基坑边缘距离的逐渐增加,地表沉降逐渐减小,变形规律较为单一。

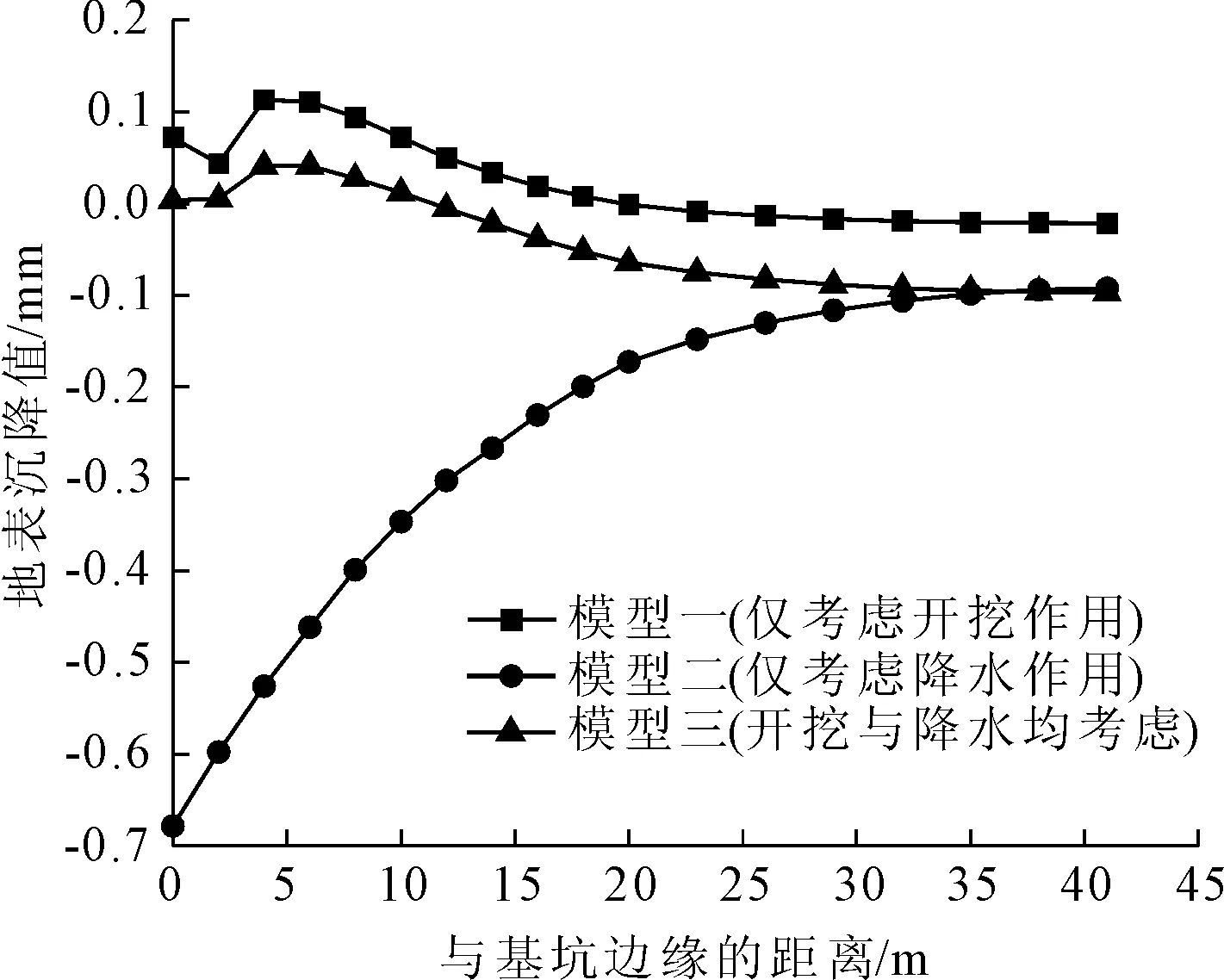
图5 第一步开挖后各模型地表沉降对比图

在距基坑边缘0 m～20 m范围内,模型一、模型二与模型三对应位置的沉降差值见表3。由表中数据可知,随着与基坑边缘距离的逐渐增加,模型一与模型三的沉降差值相对比较稳定,始终在0.061 mm附近上下波动。模型二与模型三的沉降差值随着与基坑边缘距离的增加不断减小,由最大差值0.68 mm减小到了0.11 mm,减小了约83.82%,但总体而言,普遍大于前者。由此可知,在该区间内,基坑开挖对周边地表沉降的影响程度较为稳定,而基坑降水对周边地表沉降的影响程度却在不断增大。

表3 模型一、模型二与模型三对应位置沉降差值表

在距基坑边缘21 m～41 m范围内,模型一、模型二与模型三对应位置的沉降差值见表4。由表中数据可知,随着与基坑边缘距离的逐渐增加,模型一与模型三的沉降差值逐渐增大,由0.067 mm增大到0.076 mm,增大了约13.43%。模型二与模型三的沉降差值逐渐减小,差值由-0.072 mm减小到约0.0043 mm,减小了近1倍,但总体而言,普遍小于前者。并且在距基坑边缘约23 m位置处,两模型与模型三的沉降差值十分接近。这表明,在该区间内,基坑开挖对周边地表沉降的影响程度逐渐减小,而基坑降水对周边地表沉降的影响程度仍在不断增大,且在距基坑边缘约23 m处,两者的影响程度几乎等同。

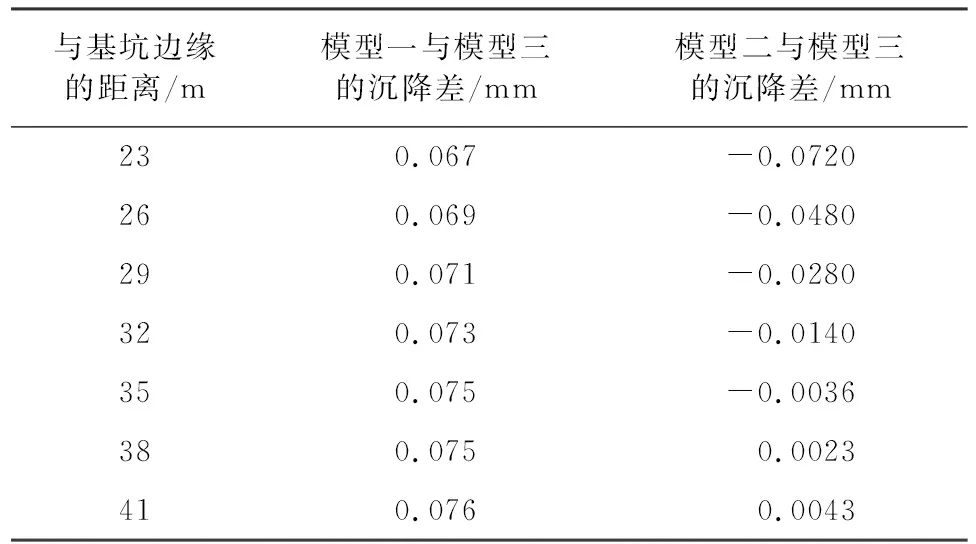
表4 模型一、模型二与模型三对应位置沉降差值表

由上述分析可知,在第一步开挖或降水结束时,随着与基坑边缘距离的逐渐增加,开挖作用对周边地表沉降影响程度的变化规律为先稳定后下降;降水作用对周边地表沉降影响程度的变化规律为不断提高,且在距基坑边缘约21 m～23 m范围内,两者的影响程度几乎等同。故对于基坑工程而言,在地表刚刚由于施工的影响而产生沉降时,沉降区域内便存已经存在一个界线,该界线位于距基坑边缘约21 m～23 m(1.69H～1.85H)范围内,将基坑周边地表沉降区域划分为两个沉降主导区,界线以里为开挖主导沉降区,界线以外为降水主导沉降区。

3.2 第二步开挖后的地表沉降数据分析

各模型第二步开挖或降水后的地表沉降对比图如图6所示。由图6可知,模型一与模型三的沉降变化规律大体相同,随着与基坑边缘距离的逐渐增加,均呈现出先增大后减小并逐渐趋于稳定的变化规律,且均于距基坑边缘约5 m处达到最大值。模型二的地表沉降分布依旧呈现“漏斗”状,即随着与基坑边缘距离的逐渐增加,地表沉降逐渐减小。

同时,由图6可知,模型二与模型三的沉降差值较为混乱,不利于分析。于是将图6中的数据与图5中的数据做差,得出基坑在第二步开挖或降水完成后相较于前一相同施工步骤的地表沉降差值对比图如图7所示。由图7可知,模型一与模型三的沉降差值变化规律较为相似,随着与基坑边缘距离的逐渐增加,先增大后减小并逐渐趋于稳定。模型二的沉降差值分布呈现“漏斗状”,即随着与基坑边缘距离的逐渐增加,沉降差值逐渐减小。

图6 第二步开挖后各模型地表沉降对比图

图7 第二步开挖后各模型地表沉降与第一步差值对比图

为保持分析方法的统一性,假设沉降差值间的差值为α。在距基坑边缘0 m～4 m范围内,模型一、模型二与模型三对应位置的α值见表5。由表中数据可知,随着与基坑边缘距离的逐渐增加,模型一与模型三的α值逐渐减小,由0.25 mm减小到-0.016 mm,减小了近1倍。模型二与模型三的α值逐渐增大,由0.27 mm增大到0.75 mm,增大了约1.78倍,且普遍大于前者。由此可知,在该区间内,基坑开挖对周边地表沉降的影响程度逐渐增大,而基坑降水对周边地表沉降的影响程度却在不断减小。

表5 模型一、模型二与模型三对应位置的α值表

在距基坑边缘5 m～14 m范围内,模型一、模型二与模型三对应位置的α值见表6。由表中数据可知,随着与基坑边缘距离的逐渐增加,模型一与模型三的α值逐渐增大并趋于稳定,由0.095 mm增大到0.47 mm,增大了约4倍。模型二与模型三的α值逐渐减小,由0.67 mm减小到-0.039 mm,减小了约一倍,且与前者的大小关系发生了变化,在距基坑边缘约8 m处,模型一、模型二与模型三的α值较为接近。由此可知,在该区间内,基坑开挖对周边地表沉降的影响程度逐渐减小并趋于稳定,而基坑降水对地表沉降的影响程度却在不断增大。且在距基坑边缘约8 m(0.65H)处,两者的影响程度较为接近。

表6 模型一、模型二与模型三对应位置的α值表

在距基坑边缘15 m～41 m范围内,模型一、模型二与模型三对应位置的α值见表7。由表中数据可知,随着与基坑边缘距离的逐渐增加,模型一与模型三的α值已基本平稳,不再有显著变化。模型二与模型三的α值仍旧逐渐减小,由-0.07 mm减小到0.031 mm,减小了约1.44倍,且依旧小于前者。由此可知,在该区间内,基坑开挖对周边地表沉降的影响程度已基本稳定,而基坑降水对地表沉降的影响程度依旧在不断增大。

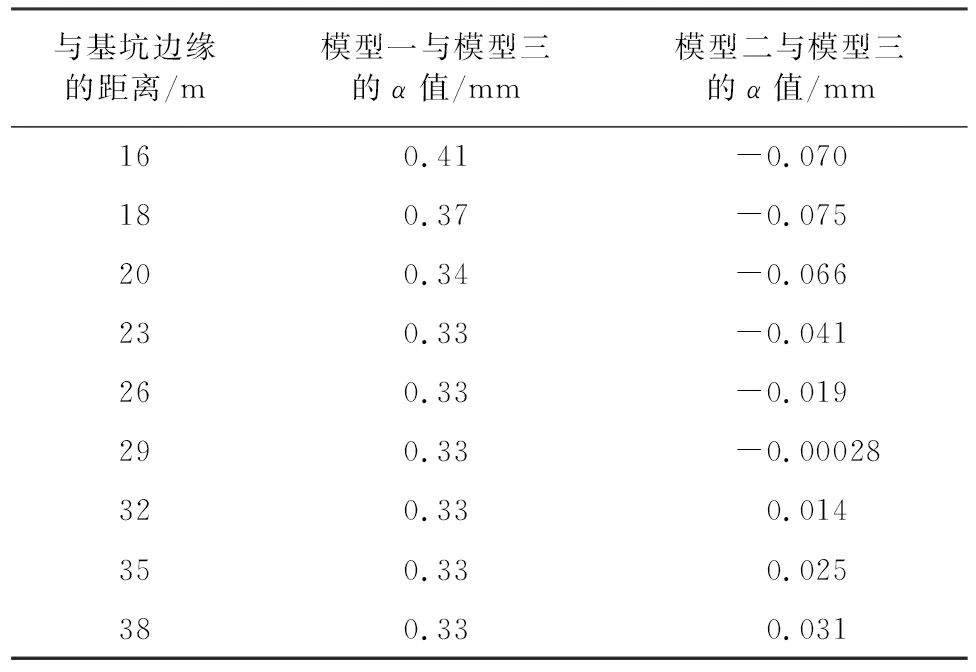
表7 模型一、模型二与模型三对应位置的α值表

由上述分析可知,在第二步开挖或降水结束后,随着与基坑边缘距离的逐渐增加,开挖作用对周边地表沉降影响程度的变化规律为先增大后减小最后趋于稳定;降水作用对周边地表沉降影响程度的变化规律为先减小后增大,且在距基坑边缘约8 m(0.65H)处,两者的影响程度几乎等同。故对于基坑工程而言,在地表由于第二次施工扰动而产生沉降时,沉降区域依旧存在一个界线,该界线位于距基坑边缘约8 m(0.65H)处。界线以里为开挖主导沉降区,界线以外为降水主导沉降区。

3.3 第三步开挖后的地表沉降数据分析

延续第3.2小节的分析思路,将基坑第三步开挖或第三步降水后的周边地表沉降数据与基坑上一施工阶段结束时的地表沉降数据做差。得出基坑在第三步开挖或降水后相较于前一相同施工步骤的地表沉降差值对比图如图8所示。由图8可知,模型一与模型三的沉降差值分布规律大体相同,随着与基坑边缘距离的逐渐增加,先增大后减小并逐渐趋于稳定。模型二的沉降差值分布较为均匀,近似为一条水平的直线。

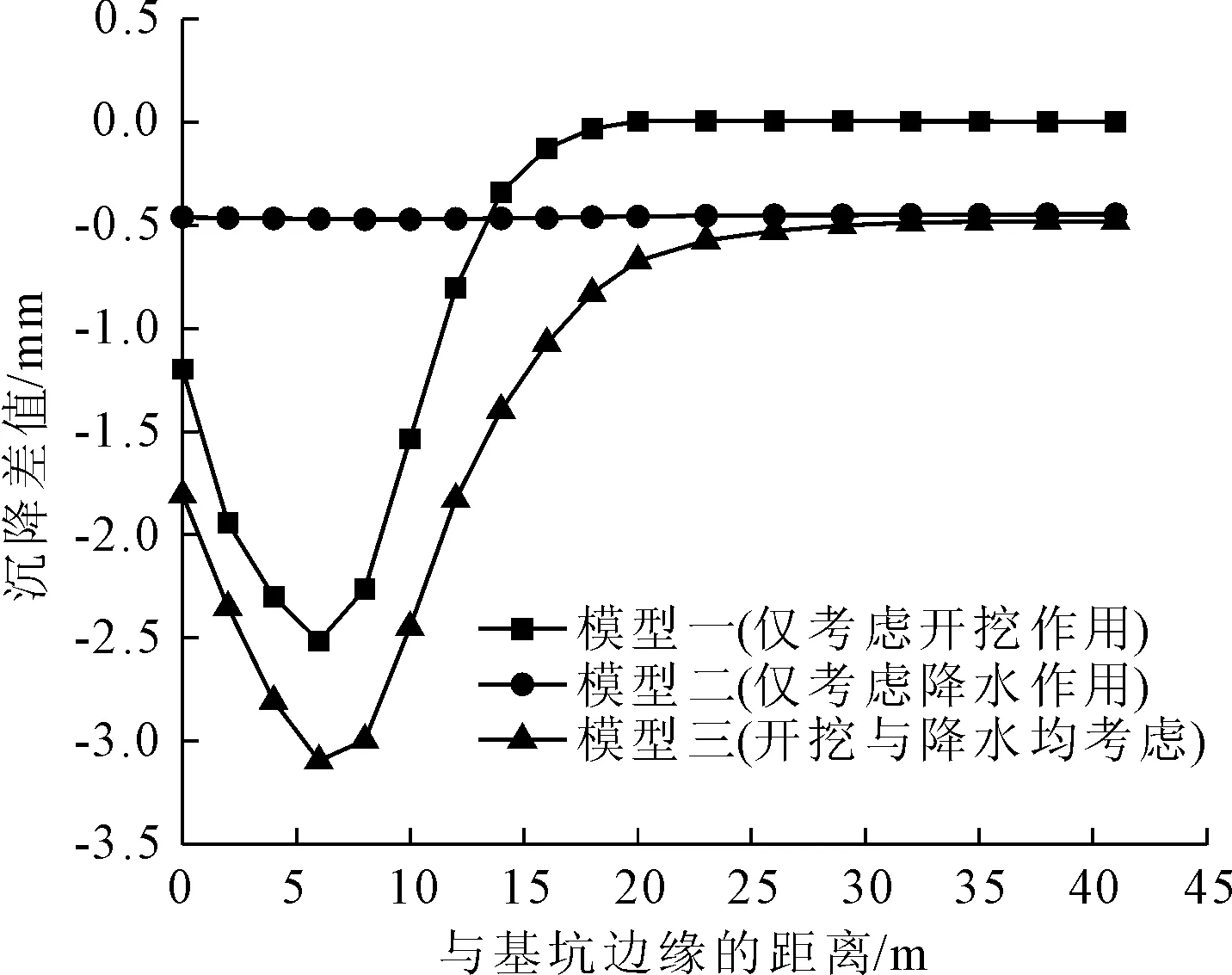
图8 第三步开挖后各模型地表沉降与第二步差值对比图

在距基坑边缘0 m～12 m范围内,模型一、模型二与模型三对应位置的α值见表8。由表中数据可知,随着与基坑边缘距离的逐渐增加,模型一与模型三的α值先减小后增大,模型二与模型三的α值先增大后减小,且普遍大于前者。在距基坑边缘10 m～12 m范围内,两组数据较为接近。由此可知,在该区间内,基坑开挖对基坑周边地表沉降的影响程度为先增大后减小,而基坑降水对基坑周边地表沉降的影响程度为先减小后增大。

表8 模型一、模型二与模型三对应位置的α值表

在距基坑边缘13 m～41 m范围内,模型一、模型二与模型三对应位置的α值见表9。由表中数据可知,随着与基坑边缘距离的逐渐增加,模型一、模型二与模型三的α值均逐渐减小,且在距基坑边缘约14 m处两组数据较为接近。但两组数据总体上的大小却完全不同,模型二与模型三的α值普遍小于前者,前者的α平均值约为0.64 mm,后者的平均值仅约为0.23 mm。由此可知,在该区间内,虽然基坑开挖与降水对周边地表沉降的影响程度均逐渐增大,但后者仍旧占据主导地位。

表9 模型一、模型二与模型三对应位置的α值表

由上述分析可知,在第三步开挖或降水结束后,随着与基坑边缘距离的逐渐增加,开挖作用对周边地表沉降影响程度的变化规律为先增大后减小再增大,最终趋于稳定;降水作用对周边地表沉降影响程度的变化规律为先减小后持续增大,且在距基坑边缘约10 m～14 m(0.81H～1.13H)范围内,两者的影响程度几乎等同。故对基坑工程而言,当地表在最后一道施工工序结束并发生沉降时,沉降区域依然存在一个界线,该界线位于距基坑边缘约10 m～14 m(0.81H～1.13H)范围内。界线以里为开挖主导沉降区,界线以外为降水主导沉降区。

综上所述,在考虑流固耦合的情况下,对于基坑工程的任意一个施工阶段,基坑周边地表沉降区均存在沉降主导界线,界线以内为开挖主导沉降区,界线以外为降水主导沉降区。随着施工进程的逐步推进,沉降主导界线的位置在不断变化,由最初的位于距基坑边缘约21 m～23 m(1.69H～1.85H)范围内,移动到距基坑边缘约8 m(0.65H)处,后移动到距基坑边缘约10 m～14 m(0.81H～1.13H)范围内,即先向基坑内侧移动后又向基坑外侧移动。

分析原因,界线存在的主要原因为基坑开挖与基坑降水所导致基坑周边地表沉降的范围、大小及分布情况都不相同。以最后一道施工工序为例,模型一与模型二的最终土体沉降剖图如图9与图10所示。由图9可知,基坑开挖导致基坑周边11.6 m范围内的土体发生了沉降,最大沉降达到了3.44 mm。由图10可知,基坑降水导致基坑周边30.6 m范围内的土体发生了沉降,最大沉降达到了1.1 mm。由此可知,基坑周边邻近土体的沉降主要由基坑开挖所主导,而较远处土体的沉降则主要由基坑降水所主导。

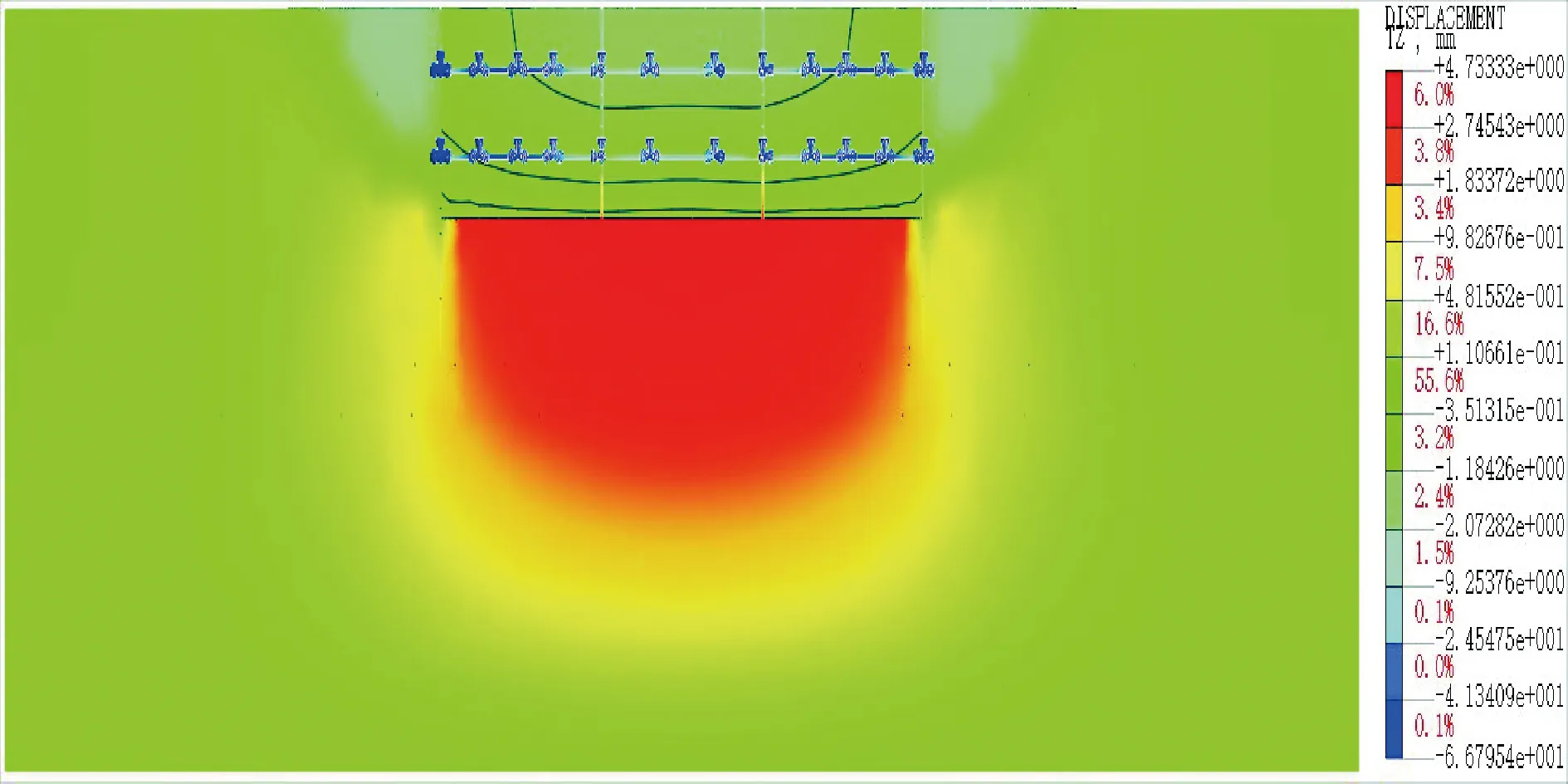
图9 模型一最终沉降剖图

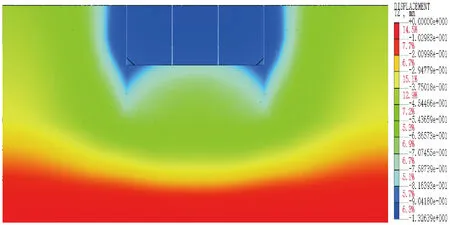
图10 模型二最终沉降剖图

界线移动的主要原因为不同步骤的基坑开挖与降水对土体的扰动程度是不同的。依旧以模型一与模型二为例,模型一与模型二第一步开挖或降水后的地表沉降矢量图如图11与图12所示。由图11与图12可知,模型一在第一步开挖结束后的地表位移矢量基本指向上,而模型二在第一步降水完成后的地表位移矢量基本指向下,因此此时的界线相对靠外。

图11 模型一第一步开挖后的地表沉降矢量图

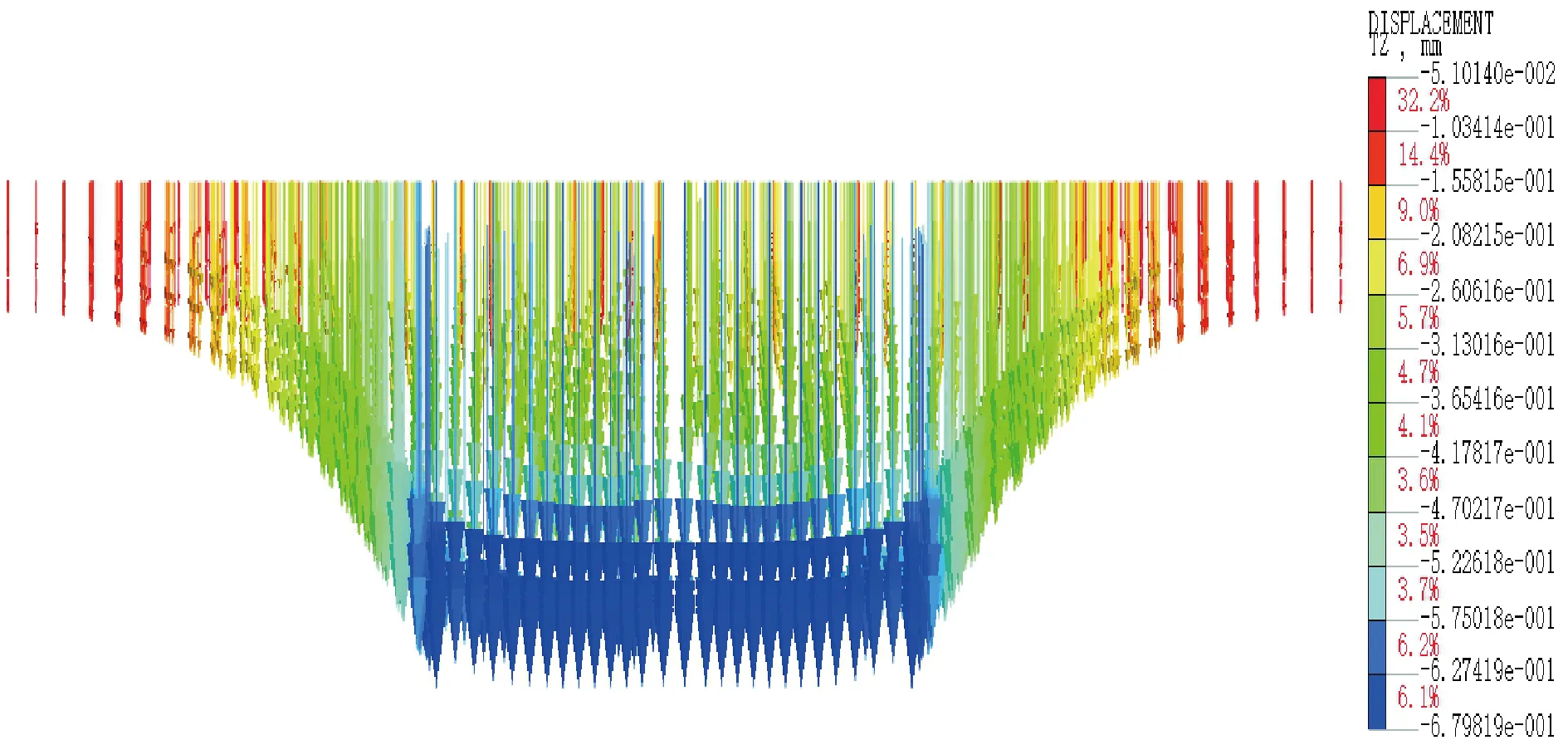
图12 模型二第一步降水后的地表沉降矢量图

模型一与模型二第二步开挖或降水后的地表沉降矢量图如图13与图14所示。由图13与图14可知,模型一在第二步开挖结束后,地表位移矢量发生了较大变化,不仅沉降矢量的大小发生变化,方向也发生了逆转,而模型二在第二步降水完成后的地表位移矢量仅有数值大小上的较小变化,因此此时的界线相对靠向基坑。

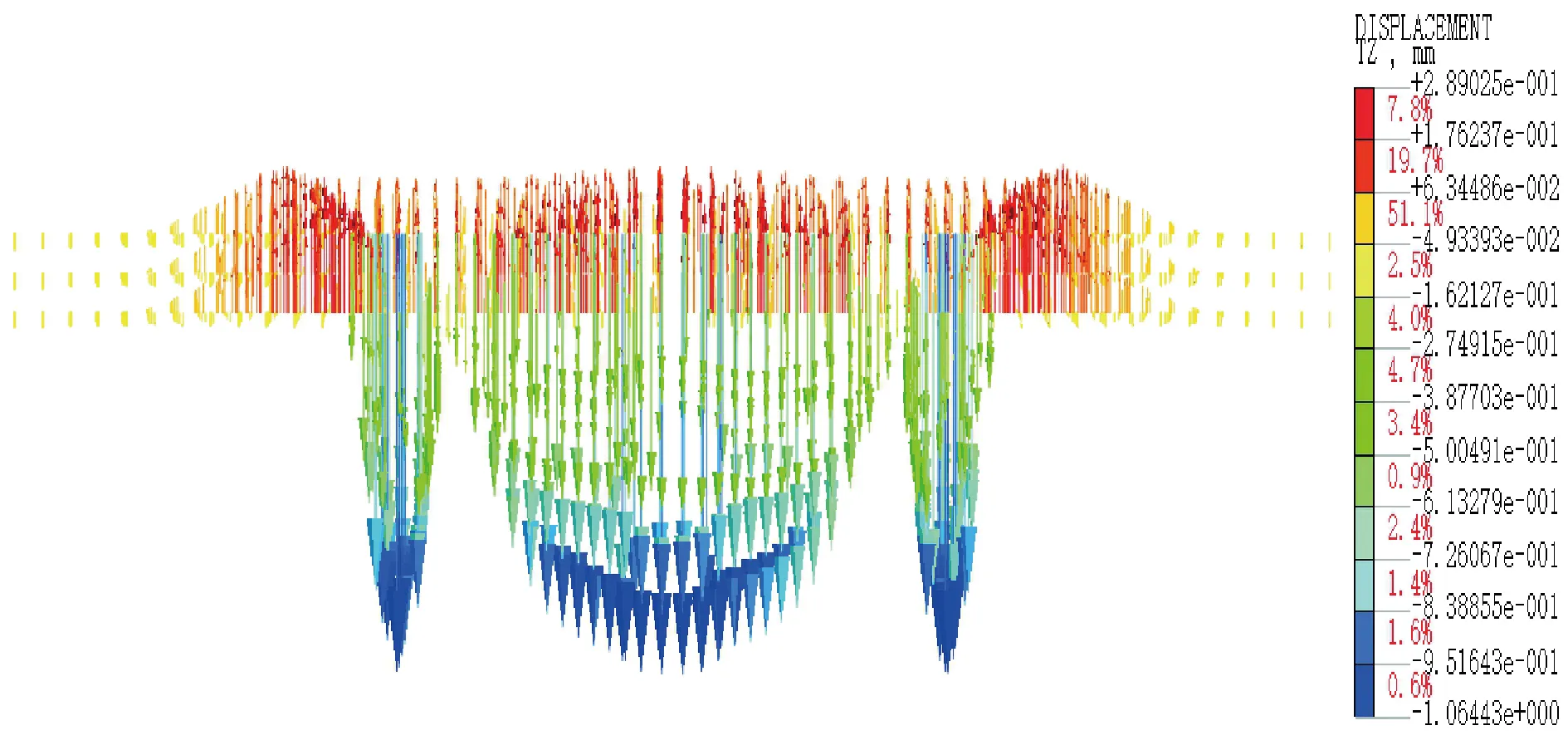
图13 模型一第二步开挖后的地表沉降矢量图

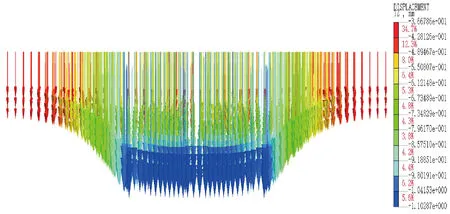
图14 模型二第二步降水后的地表沉降矢量图

模型一与模型二第三步开挖或降水后的地表沉降矢量图如图15与图16所示。由图15与图16可知,两模型此阶段的地表沉降矢量方向均向下,不同之处为模型一的矢量变化范围较小,而模型二变化范围较大,因此此时的界线会在上一阶段位置的基础上向坑外侧做少许移动。

图15 模型一第三步开挖后的地表沉降矢量图

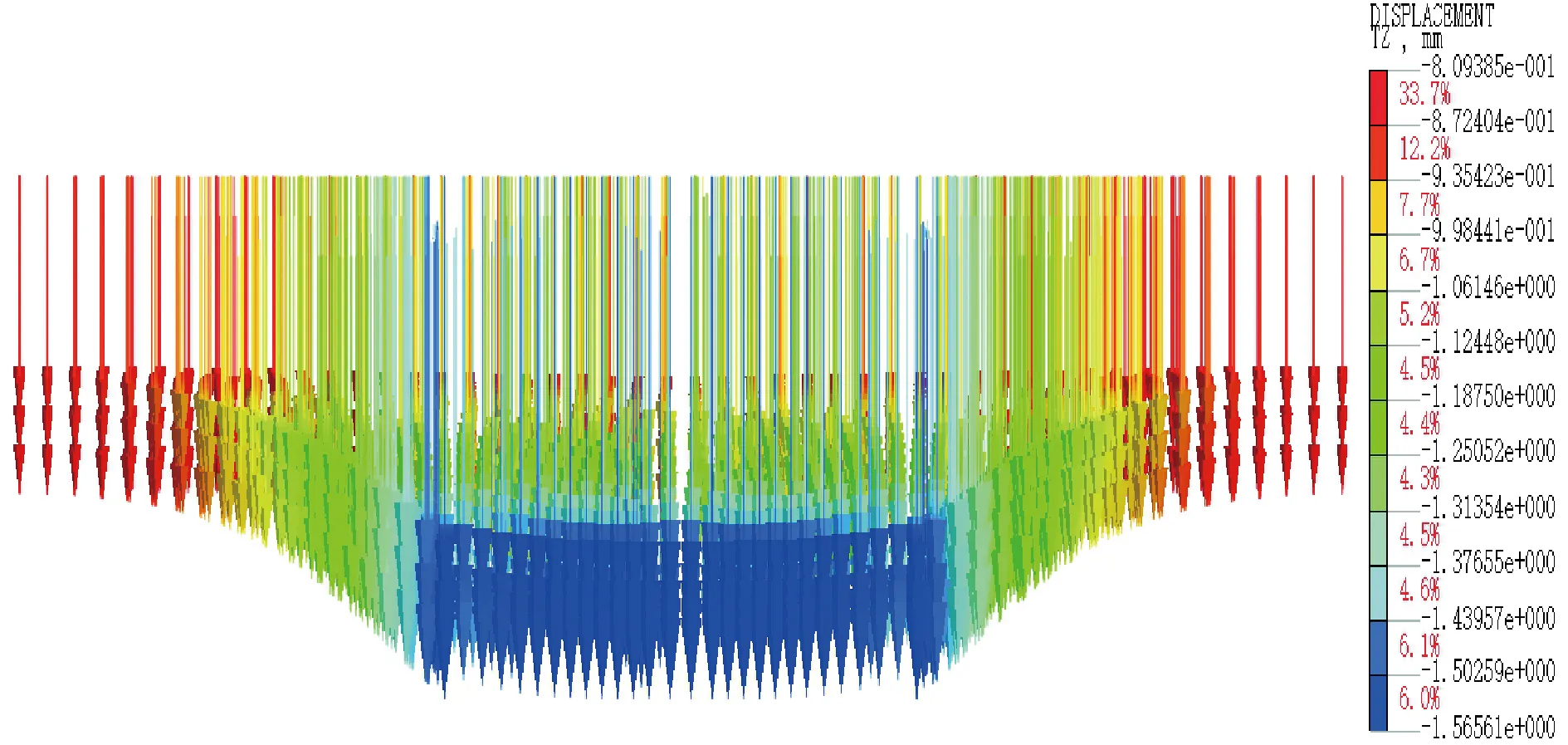
图16 模型二第三步降水后的地表沉降矢量图

4 结 论

本文以广州市某建筑基坑工程为背景,基于流固耦合模型与三维固结理论,应用有限元软件midas GTS NX模拟分析不同工况下的基坑周边地表沉降变形。研究了基坑周边地表沉降区存在沉降主导界线的问题,为未来探索高精度控制基坑周边地表沉降提供参考。主要结论如下:

(1) 基坑周边地表沉降区存在一个将沉降分为不同因素主导的界线,界线以里为开挖主导沉降区,界线以外为降水主导沉降区。

(2) 随着施工进程的推进,界线的位置在不断变化。界线最初位于距基坑边缘约21 m～23 m(1.69H～1.85H)范围内,移动到距基坑边缘约8 m(0.65H)处,后移动到距基坑边缘约10 m～14 m(0.81H～1.13H)范围内。

(3) 在实际工程中,应根据被保护建(构)筑物所处的位置与所关注的施工进程,先判断其所在区域沉降的主导因素,然后采取针对性措施,以达到更加精确控制深基坑周边地表沉降的目的。