注塑机筒疲劳强度计算的设计准则

袁卫明，成明祥

(德清申达机器制造有限公司，浙江 湖州 313205)

0 引言

注塑机机筒是注射机构中的重要零部件，在工作中其要承载注射高压的冲击，当前注塑机的注射压力已从传统的170 MPa发展到270 MPa以上。面对机筒在高压和超高压中出现的失效现象，沿用传统的注塑机筒强度理论[1]，不能圆满解释机筒失效的实际现象。本文从厚壁圆筒的弹塑性力学理论[2]分析研究注塑机筒的工作特性，阐述以往用弹性力学角度分析研究机筒强度的局限性，提出了符合实际的注塑机筒疲劳强度的设计准则，并用实例加以论证。

1 厚壁圆筒

1.1 厚壁圆筒的应力分析

根据厚壁圆筒体[3]的应力变形特点，我们假设将厚壁圆筒看成是由许多个薄壁圆筒相互连在一起所组成，如图1所示，当厚壁圆筒内径承受内压力后，其组成的各层薄壁圆筒由里至外逐步受力，其变形受到里层薄壁圆筒的约束和受到外层薄壁圆筒的限制，因此各个单元薄壁圆筒体都会受到内外侧变形的约束和限制所引起的均布压力作用，从里往外各层薄壁圆筒体的变形被受到的约束和限制是不同的，环向应力沿壁厚方向分布是不均匀的，这是厚壁圆筒形变和应力的一个基本特点。

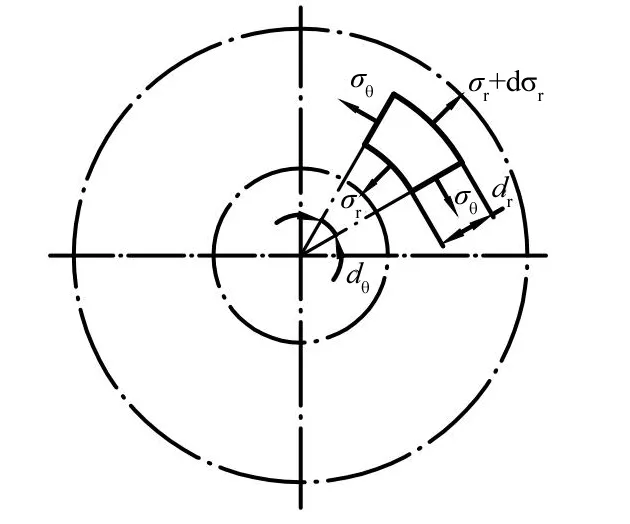
图1 厚壁圆筒应力分布图

厚壁圆筒应力、应变的另一个特点是：由于厚壁圆筒是由多个薄壁圆筒组成，在多层材料变形的相互约束和限制下，沿径向方向产生了径向应力，沿壁厚方向径向应力分布是不均匀的。厚壁圆筒和薄壁圆筒在两端封闭状态时，沿轴线方向产生的轴向应力则是相同的，且轴向应力沿壁厚方向分布是均匀的。

在厚壁圆筒受内压力时，各应力分量沿壁厚分布[4]情况如图2、3所示，其中最大环向应力点发生在内壁，最小环向应力点发生在外壁[3]。

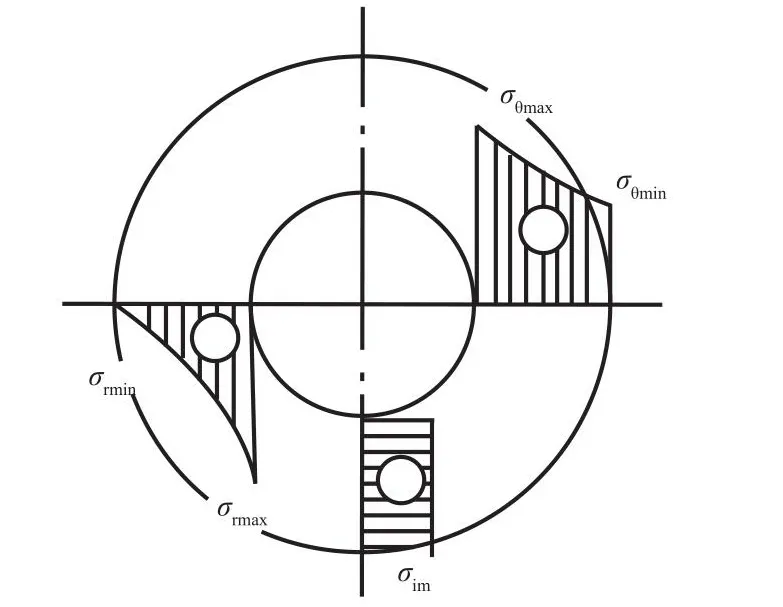
图2 受内压厚壁圆筒应力分量沿壁厚分布图

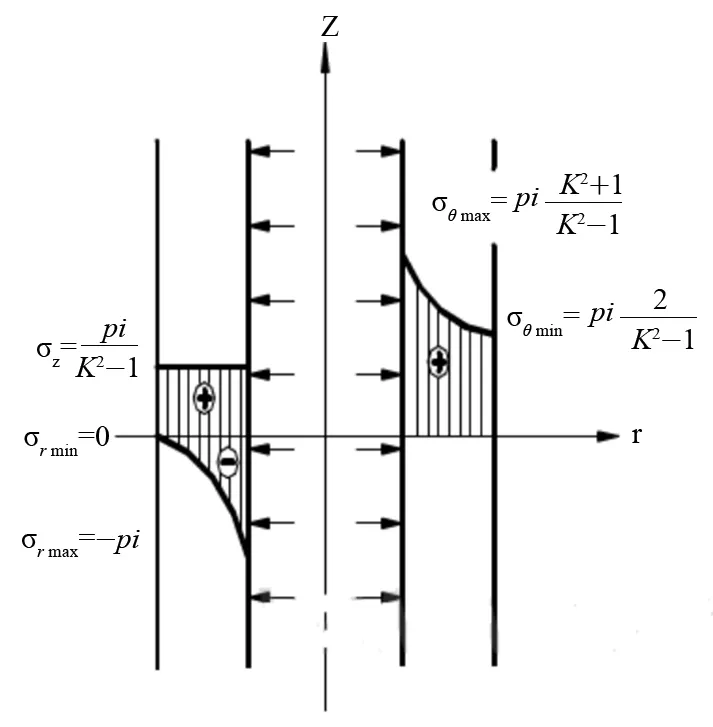
图3 受内压厚壁圆筒中各应力分量分布图

σθ—环向应力，沿壁厚方向非均匀分布；

σr—径向应力，沿壁厚方向非均匀分布；

σz—轴向应力，沿壁厚方向均匀分布。

由于环向、径向和轴向三个应力分量的存在，并且径向应力σr和环向应力σθ分布又是非均匀性的，因此厚壁和薄壁圆筒的应力分析方法会有较大的差异。在计算应力强度时，必须分别求出三个主应力σθ、σz、σr，再根据第三或第四强度理论公式计算得出应力强度值，计算结果与许用应力进行比较判断。

1.2 厚壁圆筒应力计算公式

厚壁圆筒应力计算公式既适用于厚壁也适用于薄壁圆筒。下面将厚壁圆筒中的最大环向应力σθmax与最小环向应力σθmin作一比计算较分析，厚壁圆筒受内压力时其值按表1 所示。

表1 受内压力的厚壁圆筒应力计算公式

两者之比：

式中：Pi—圆筒所受内压力；

Da—圆筒内径；

Db—圆筒外径；

K—径比。

当圆筒壁较薄时，Db≈Da、K≈1,则(K2+l)/2≈1。即σθmax≈σθmin，即圆筒内外径趋于接近时，内外壁的应力也趋于相等，应力沿壁厚方向趋于均匀分布。

当圆筒的壁厚增加时，径比值K也增加，最大与最小的环向应力比值 (K2+1) / 2 也随着增加，即σθmax与σθmin的差值越来越大。亦即应力σθ沿壁厚方向分布的非均匀性增加。当K=1.1时，内外壁的应力值会相差10%，当K=1.3时，内外壁的应力值就会相差35%。因此工程上一般用径比值K=1.1～1.2来规定厚壁与薄壁圆筒的界限区分。

2 传统机筒疲劳强度设计

2.1 注塑机筒疲劳强度分析对象

注塑机在注射过程中一般可分额定注射行程段为压力注射，注射至结束段为高压注射。机筒疲劳失效主要现象是头部高压区的径向平面内产生径向裂纹由内到外延伸，并在该平面内沿径向一直扩展至机筒外壁，裂纹1～2条，表观显示出机筒疲劳强度不足。因机筒头部处于高压段是机筒疲劳强度最薄弱处，因此是机筒分析疲劳强度的重点[5]。

目前机筒头部结构与喷嘴座连接一般分两种形式：直筒型螺钉联接如图4和阶梯式螺钉联接如图5。图示中的（网格区）是疲劳强度薄弱处的计算截面。图中，r1为机筒疲劳强度计算截面内半径，r2为截面外半径。

图4 机筒头部螺钉联接式的直筒型机筒

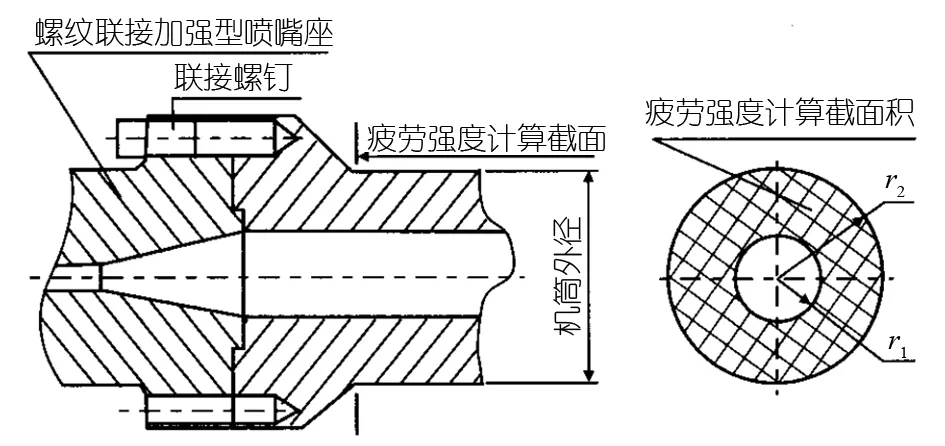
图5 机筒头部螺钉联接式的阶梯型机筒

2.2 注塑机筒弹性力学分析

机筒为两端通孔的厚壁圆筒，设内半径为r1，外半径为r2，机筒任意点半径为r，受均匀工作内压力P作用，外压为0。机筒应力应变是厚壁圆筒的一个轴对称的平面应变，其应力分析模型[6]见图6，其σθ、σz、σr沿壁厚的分布[7]见图7。机筒的应力计算见表1厚壁圆筒应力(σθ、σz、σr)公式。

图6 机筒应力分析模型

图7 机筒应力σθ、σz、σr沿壁厚的分布

2.3 传统注塑机筒疲劳强度理论

根据塑料机械设计教材[1]资料，对机筒受力状况，可按厚壁筒计算中的能量理论，校核其强度或计算壁厚。

机筒的总应力：

机筒壁厚：

式中：P—注射压力；

Da—机筒内径；

[σ]—材料许用应力；

σs—材料屈服极限；

n—安全系数，一般取1.5～2。

以传统的注塑机为例，机筒材料38CrMoAL，注射压力P=170 MPa，机筒头部为疲劳强度薄弱处，结构如图4所示，机筒径比K值按塑料机械设计教材，表2的数值代入公式（3），可得机筒应力值如下表2：

表2 注塑机筒应力值

根据文献[1]推荐材料的屈服强度σS=575 MPa，安全系数n=1.65，则许用应力[σ]=348 MPa。从表2计算结果可知机筒应力值σ＞[σ]，结果为不安全，这个与实际使用情况不相符存在矛盾。

3 厚壁圆筒的弹塑性力学分析

厚壁圆筒是高压和超高压工程中的主要承压容器，由于其承受的压力较高，因而一般均用强度和韧性较好的有强化材料制成。厚壁圆筒在承受内压力作用时，随着压力的增加筒壁应力也不断增高。当三个应力分量达到某一组合值时，厚壁圆筒发生的变形会由弹性状态进入塑性变形状态，从厚壁圆筒的截面上看有塑性变形出现，由内壁开始形成塑性区逐渐向外壁表面扩展，直到筒壁全部被屈服。

从弹性力学角度分析，当材料处于弹性范围时，物体受载后的应力-应变服从虎克定律，同时加载、卸载时的应力和应变始终保持一一对应的线性关系。当应力超过屈服点而处于塑性状态时，需用塑性力学进行分析，由于应力和应变关系呈非线性，且不相互对应，即应力不仅取决于最终的应变，而且也跟加载的方法有关[2]。

排除材料在塑性变形过程中的塑性强化因素，将厚壁圆筒作为理想弹塑性体，那么以筒体的内半径为Ri，外半径为Ro，筒体仅受内压Pi作用时需按弹性极限、弹塑性应力和塑性极限三方面加以分析。

为了充分发挥材料的承载潜力，在高压尤其是超高压场合，厚壁圆筒的静态强度设计，一般采用弹性准则、塑性准则或爆破准则。根据所采用的塑性屈服条的不同，塑性准则有两种形式：基于Tresca屈服条件的塑性准则和基于Mises屈服条件的塑性准则[8]。

3.1 弹性极限设计准则

按弹性极限理论分析[2]：当厚壁圆筒体仅受内压力Pi作用时，在内压力Pi较小时，圆筒体处于弹性状态，当内压力升高到达圆筒体的某一极限压力Pi=Pe时，圆筒体的内壁首先会开始产生屈服现象。如将圆筒体总体部位的初始屈服视为失效，则工程中，常常将等效应力控制在许用应力之内，即σ≤［σ］。

按第四强度理论（变形能理论）[9]：

将表1中受内压厚壁圆筒的内壁应力σ1、σ2、σ3代入公式（6）可得内压厚壁圆筒的合成应力：

内压厚壁圆筒能够承受的压力：

相应的筒体计算厚度为：

试验发现：基于拉美公式和第四强度理论预测的圆筒初始屈服压力与实测值最为接近，因此与第四强度理论对应的等效应力能较好地反映圆筒的实际应力水平[10]。

3.2 弹塑性应力设计准则

按弹塑性应力分析[2]：当Pi＞Pe时，圆筒体内壁屈服的区域就会向外扩展，沿圆筒体壁厚方向就会形成两个不同区域如图8，内侧为塑性区，外侧为弹性区[4]。圆筒体的弹性和塑性区会形成一个交界面，并且是一个与圆筒体同心的圆柱面，界面圆柱的半径为Rc。由于在塑性区域存在塑性变形，圆筒体内壁应力会发生重新分布，圆筒体内壁表面应力会有所下降，见图9弹-塑性区的应力分布。

图8 处于弹塑性状态的厚壁圆筒

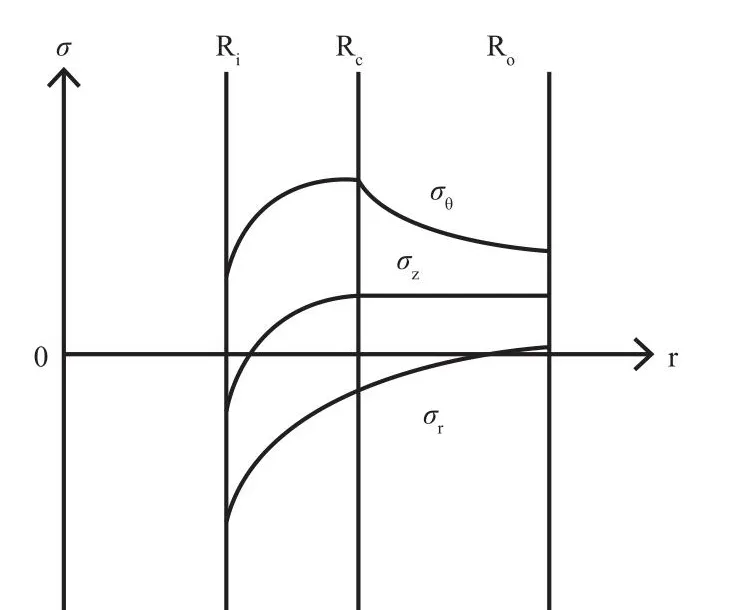
图9 弹-塑性区的应力分布

弹性失效设计准则是以危险点的等效应力达到许用应力作为失效判据的。对于应力分布不均匀的构件，如厚壁圆筒，由于材料塑性较好，当内壁材料屈服时，内壁面以外的材料仍处于弹性状态，故不会导致整个截面屈服，圆筒仍能继续承载[11]。因此，在这种情况下，弹性失效设计准则显得有所保守。

3.2.1 塑性区（Ri ≥r≤ Rc）

材料处于塑性状态时，设材料塑性变形时应力

若符合Tresca屈服条件，则弹-塑性区交界面Rc压力为：

若符合Mises屈服条件，则弹-塑性区交界面Rc压力为：

3.2.2 弹性区（Rc ≥r≤ R0）

弹性区的内壁面为弹-塑性区交界面，即弹性区的内壁面呈塑性状态。

若符合Tresca屈服条件则：

内压力Pi与所对应的塑性区圆柱面半径Rc之间的关系：

若符合Mises屈服条件则：

内压力Pi与之所对应的塑性区圆柱面半径Rc之间的关系：

3.3 塑性极限设计准则

按塑性极限理论分析[2]：当内压力p不断增大时，塑性区域会不断的扩大，弹性区域则不断的缩小。当内压力增大到某一值时，塑性区就会被扩展到整个圆筒体，即RC=R0时，则圆筒体全部进入塑性状态。塑性极限设计准则假设材料为理想弹塑性，以整个危险截面屈服作为失效状态的设计准则。

3.3.1 基于Tresca 全屈服压力

按Tresca 屈服失效判据，可得内压厚壁圆筒能够承受的压力：

相应的筒体计算厚度为：

3.3.2 基于Mises 全屈服压力

按Mises 屈服失效判据，可得内压厚壁圆筒能够承受的压力：

相应的筒体计算厚度为：

图10示出按塑性失效设计准则时，圆筒的承载能力和径比 k 的关系[11]。可以看出，按塑性失效准则在同一承载能力下，Tresca 全屈服压力算出的壁厚较厚，Mises 全屈服压力算出的壁厚较薄；当径比较小时，两种设计准则差别不大。

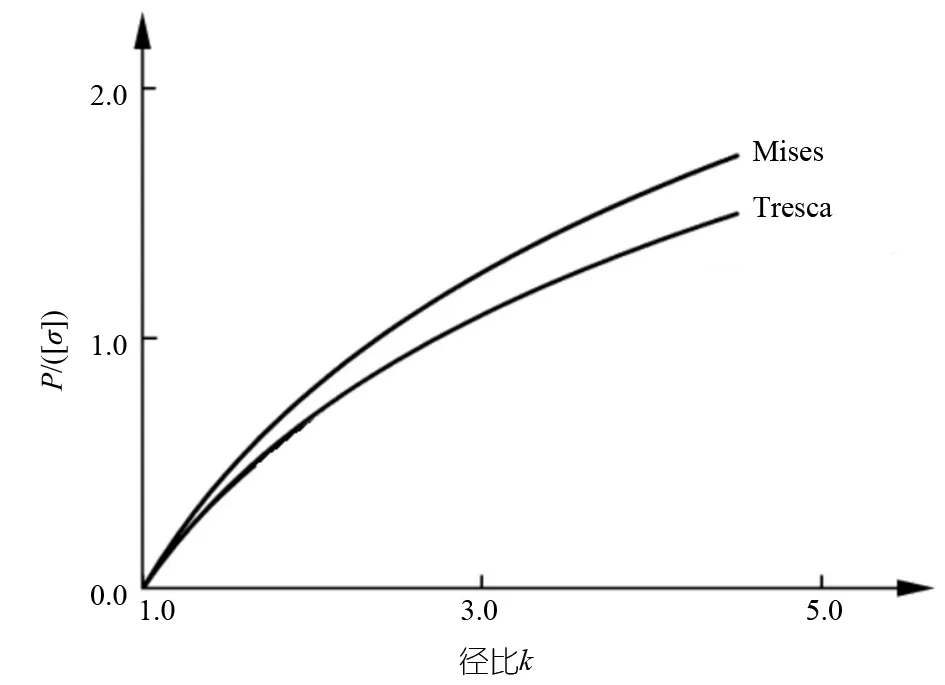
图10 塑性失效准则时圆筒承载能力和径比关系

4 分析讨论

对比公式（3）和（7）可知，其表达内容是一致的，由此可知塑料机械设计教材[1]关于机筒强度的计算校核是基于弹塑性力学中的弹性极限设计准则判据的，即以危险点的等效应力达到许用应力作为失效判据。由于注塑机筒属于厚壁圆筒，机筒材料受力关系是非线性的，因此用弹性失效分析具有保守性和局限性，不能充分发挥材料的强度潜力。

根据对三种“失效”的理论分析，弹性失效虽然比较成熟，但是，还是采用塑性失效设计准则计算的圆筒体强度作为依据比较合理[12]。近年来，由于厚壁圆筒的广泛应用和对其研究的重视，提出运用按塑性失效准则对其进行弹塑性力学行为分析[13]。若表2按塑性极限准则的Tresca屈服失效判据计算，可得表3结果。

表3 注塑机筒能承受的压力值

由表3可知，各机筒直径的承压值均大于实际注射压力170 Mpa，因此上述机筒壁厚可以满足实际使用。由此推断在注塑机筒设计中对于k＞1.5(即p＞0.4[σ]）的机筒，可以采用Tresca 全屈服压力进行其压力、壁厚计算校核，符合机筒实际运用状态。

5 计算实例

以文献资料[14]例1，机筒头部疲劳强度薄弱区最大内径Da=40 mm，工作压力P0=275 MPa，材料38CrMoAL屈服极限σS＝575 Mpa，安全系数n=1.5，则许用应力 [σ]=385 Mpa。

由式（16）、（17）计算可得：

机筒径比：K=2.042；

机筒壁厚：S=22.22 mm；

机筒外径：Db=Da+2S=40+2×22.22=84.44 m。

计算结果与文献资料作者提出的机筒壁厚（径比K值）设计准则基本相一致，符合实际。

6 结论

注塑机筒材料塑性较好，采用传统的弹性失效设计准则具有所保守，而按塑性极限设计中的Tresca 全屈服失效准则可得到较正确的计算结果，符合机筒的一般设计分析。由于机筒疲劳强度问题受材料工艺、热处理等影响较复杂，在理论上较难获得一个普遍适用的设计准则，对当前一些设计准则难以得出定量、准确的结论，但对从事相关研究者具有很大的价值意义。