基于混合整数规划的工厂产品托盘打包及装箱问题研究

张晶蓉，贺占文，周艳杰，李玉民

自动化与智能化技术

基于混合整数规划的工厂产品托盘打包及装箱问题研究

张晶蓉，贺占文，周艳杰*，李玉民

（郑州大学 管理学院，郑州 450001）

针对工厂产品的托盘打包及装箱问题，提出一种优化产品在托盘上的布局以及托盘与产品整体在集装箱中的布局方法，以最大化集装箱的空间利用。在满足现实约束的条件下，以最大化产品装载体积为目标建立混合整数规划模型。考虑问题的复杂性，本文将所研究的问题分解为2个子问题，并建立两阶段装载模型进行求解。第1阶段，建立二维集装箱装载模型，确定多种托盘类型在集装箱底面的平面布局；第2阶段，建立三维托盘装载模型，确定产品在托盘上的立体布局。鉴于精确求解该问题耗时较大，本文针对2个子问题设计两阶段启发式算法求解。为验证模型及算法的有效性，采用2组不同规模大小的算例进行测试。算例结果表明，在小、大2种规模算例中，装载率平均差值分别为0和−0.5%，计算时间相差较大，本文提出的模型及算法在合理的时间内获得了最优解或近似最优解。本研究能够为工厂产品的托盘打包及装箱提供快速高效的解决方案。

集装箱；装载；托盘打包；工厂产品；混合整数规划；启发式算法

随着工厂仓库的产品数量及种类的增多，在产品出库时，托盘可将多种类型产品归置整理成规格统一且具有一定体积形状的产品单元，以促进包装的标准化与模块化。通过将产品整齐码放在托盘上、打包再到集装箱装箱，提高了整个作业流程的效率。在运输过程中，带托盘运输能有效提高装卸效率，减少人工装卸费用，减少货损，便于产品数量统计及计价，降低运输过程总时长。但大多工厂在解决产品的托盘打包和装箱问题时，往往采用基于人工经验知识的集装箱装载和规划模式，导致集装箱装载方案的鲁棒性不高，装载率普遍较低。因此，有必要对产品的托盘打包及装箱问题进行建模与优化，以提高集装箱的空间利用率。

产品的托盘打包及装箱问题包含了集装箱装载（Container Loading Problem，CLP）和托盘装载（Pallet Loading Problem，PLP）2个经典的组合优化问题，其求解难度随变量增加呈指数级增长，因此该NP-Hard问题难以求解。启发式算法是求解这类问题的有效方法，近些年来，根据优化目标及约束条件的不同，学者们提出了相应的启发式算法。

在集装箱装载方面，尚正阳等[1]针对一刀切约束下的二维装箱问题，构建改进优先度算法求解，运行效果较优。Ignacio等[2]设计了集装箱装载率及产品价值最大化2个目标函数，利用集束搜索算法求解。刘胜等[3-4]考虑完全支撑及方向等约束条件，将树搜索的思想应用于三维装箱。Bayraktar等[5]考虑几何约束以及不重叠约束，并利用混合人工蜂群算法进行求解。张长勇等[6]考虑产品装载的顺序约束、稳定性约束、不重叠约束等，并利用基于拟人装载策略的改进遗传算法求解。王帅等[7]设计基于强化学习的方法训练所建立的装箱模型解决机场行李箱的装箱问题。吕雪菊等[8]考虑了稳定性约束、定向性以及完全切割约束，利用半径多样化小生境遗传算法进行求解。

在托盘装载方面，PLP按照所装产品类型相同或不同可分为制造商托盘装载（Manufacturer's Pallet Loading Problem，MPLP）和分销商托盘装载（Distributor's Pallet Loading Problem，DPLP）2种类型。大多学者采用将同质或异质的产品构成层，接着将产品层层堆码的方法，使托盘数量最小化，此时构成层的过程可转化为二维托盘装载[9-10]。在二维托盘装载方面，Pisinger等[11]考虑几何约束以及不重叠约束，构建混合整数规划模型，并介绍几个新的下限。Cui等[12]考虑方向性约束以及完全切割约束，并利用价值修订方程修订生成产品的价值，并利用顺序启发式算法求解。宋卫生等[13]基于4种典型的托盘堆码方式，以表面利用率最大为目标研究了货物的装载优化方式，并给出了最优排列方案。

在引入托盘的集装箱装载方面，Liu等[14]研究家具工厂产品的装载问题，考虑将已装载产品的托盘装载到集装箱后，在剩余空隙中加入未被装载的产品，从而使集装箱利用率最大，利用树搜索算法与贪婪算法实现。Alonso等[15-16]研究卡车车厢结合托盘的装载问题，该文献假设已确定好每个产品在托盘上的层布局，将产品及托盘整体装入车厢；为保证产品在车厢的稳定性，需满足多个约束条件，利用混合整数规划模型及贪心随机自适应搜索算法求解。

综上所述，目前大多数文献均是单独提高集装箱或托盘的空间利用。虽然有少量文献研究了引入托盘的集装箱装载问题，但该类文献仅考虑将托盘与产品整体装入集装箱或车厢中，未同时考虑产品的托盘打包及装箱问题，以及未考虑装载多种托盘类型。本文将产品的托盘打包及装箱过程进行统筹优化，考虑实际装载过程中的诸多约束，建立以最大化产品装载体积为目标的集装箱-托盘装载模型。为降低问题的复杂度，将所研究的问题分解为2个子问题，并建立两阶段装载模型求解。考虑到产品数量较多时模型求解困难的问题，设计两阶段启发式算法求解。本文采用2种不同规模大小的算例对所提的模型及算法进行测试，验证模型的正确性和算法的有效性、收敛性及稳定性。

1 问题描述与建模

1.1 问题描述

本文基于以下假设进行研究：工厂有多种产品类型，且每种产品类型数量充足；产品全部为规则的长方体形状；产品的重量在托盘以及集装箱承重范围之内；不考虑产品之间以及产品与托盘之间存在挤压变形的情况；托盘仅能放置在集装箱底面，以简化装卸流程；每个托盘可装载多个类型的产品；为保证装载稳定性，在产品装载完成之后，允许将托盘固定，并把缝隙填充。

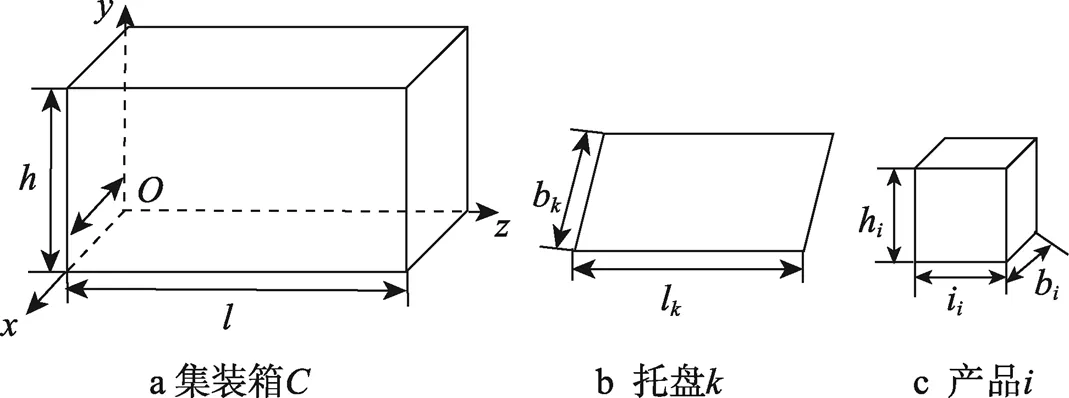
图1 坐标系以及集装箱、托盘和产品的尺寸

1.2 符号说明

本文所用的参数和变量说明见表1。

图2 不重叠约束

表1 参数符号

Tab.1 Parameter symbol

1.3 模型构建

1.3.1 集装箱-托盘装载模型

本文参考文献[7]不重叠约束的建模思路，在、、轴方向上对产品位置关系进行约束。保证任意2个产品及托盘之间不发生重叠，且不能超出集装箱的尺寸范围，建立以装载产品体积之和最大化为目标的集装箱-托盘装载模型。在集装箱装载过程中同时确定产品在托盘上的布局，以及产品和托盘整体在集装箱中的位置，其中装载在集装箱中的产品只能完全放置在一个托盘中。具体模型如下：

(2)

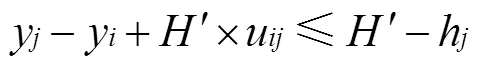
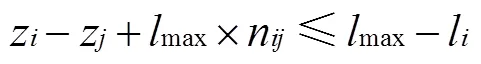
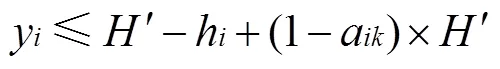
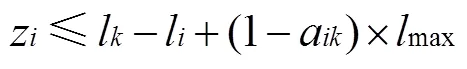
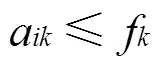
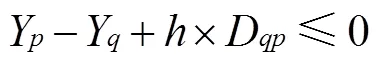
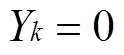
1.3.2 两阶段装载模型

由于上述集装箱-托盘装载模型复杂度高、难以求解，因此考虑将所研究的问题拆分为二维集装箱装载和三维托盘装载2个子问题，建立两阶段装载模型对2个子问题分别建模。具体步骤如下所出。

1）第1阶段。确定多种类型托盘在集装箱底面的布局。建立二维集装箱装载模型确定托盘在集装箱底面的布局，即确定装入集装箱底面托盘的种类、数量及位置，如图3所示，这些二维托盘整体形成集合。该模型以装入集装箱的托盘表面积最大化为目标函数，考虑托盘装载时的不重叠约束条件，在、轴方向上约束托盘之间的位置关系。具体的装载模型如下：

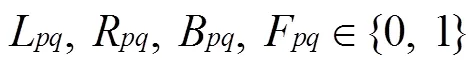
其中，式（25）为目标函数，表示装入集装箱的托盘表面积之和最大化；式（26）—式（30）确保托盘之间不发生重叠；式（31）—式（32）确保托盘的尺寸小于集装箱的尺寸；式（33）—式（35）表示决策变量约束。

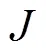
(37)

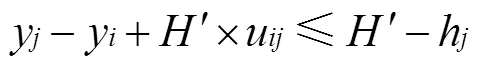
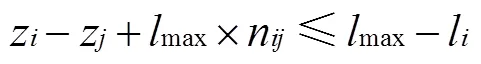
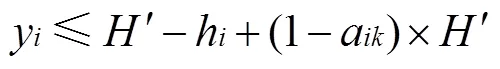
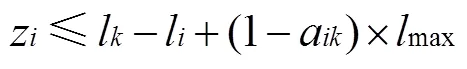
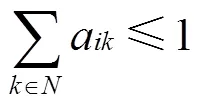
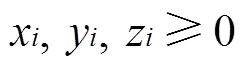
其中，式（36）为目标函数，表示装进三维托盘集合的产品的体积之和最大化；式（37）—式（43）表示确保产品之间不发生重叠；式（44）表示产品最多只能放进1个托盘中；式（45）—式（47）表示决策变量约束。

1.3.3 两阶段启发式算法

当产品数量较多时，两阶段装载模型的第2阶段利用三维托盘装载模型求解较为困难，难以在合理的时间内得到满意解。目前，已有较多文献求解该类组合优化问题[17]。考虑到求解的时效性，本文设计两阶段启发式算法进行求解，在第2阶段对三维托盘装载模型进行优化。算法步骤如下所示。

1）第1阶段。调用CPLEX求解器对二维集装箱装载模型进行求解，可以在短时间内确定多种托盘类型在集装箱底面的布局，因此不需要优化。

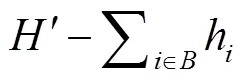
在确定产品在托盘表面的布局时，将该装载过程建立二维托盘装载模型，即在第1阶段选定的托盘表面集合和给定的产品底面集合中，计算装载托盘表面积利用率最大的产品集合。该模型以装载产品的表面积最大化为目标函数，考虑产品之间的不重叠约束条件，在、轴方向上约束产品之间的位置关系，具体的模型如下所示：

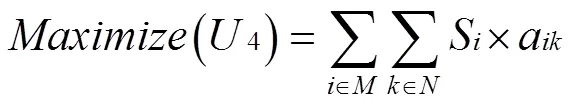
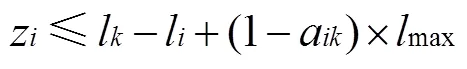
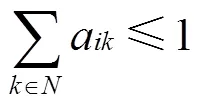
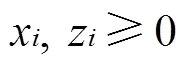
其中，式（48）为目标函数，表示装进若干个托盘的产品底面积最大化；式（49）—式（53）确保产品之间不发生重叠；式（54）表示产品最多只能放进一个托盘中；式（55）—式（57）表示决策变量约束。

2 实验方案

本文选取郑州市某食品加工厂为研究对象，以该工厂的产品托盘打包及装箱问题为例，根据实地调研资料，设置2组规模大小的算例数据，以验证模型的正确性及算法的有效性与寻优性。

图3 启发式三维托盘装载示意图

本文利用Matlab完成数据的输入输出处理，并利用IBM ILOG CPLEX12.8对建立的模型进行求解。实验程序运行在Intel(R) Core(TM) i7-7500U CPU@2.70 GHz 2.90 GHz处理器上，运行环境为Windows 10企业版。

2.1 实验参数设置

本文设置2种规模大小的算例数据，小规模算例有6种产品类型，大规模算例有12种产品类型，各设置5组实验，每组实验由10个算例构成。在2组算例中，根据实地调研资料，将产品数据利用Matlab中的（）函数在区间范围内随机生成，托盘选自该食品加工厂使用的托盘类型，集装箱尺寸为标准20英尺（1英尺=0.304 8米）。算例的具体数据来源及范围如表2所示。

2.2 小规模算例

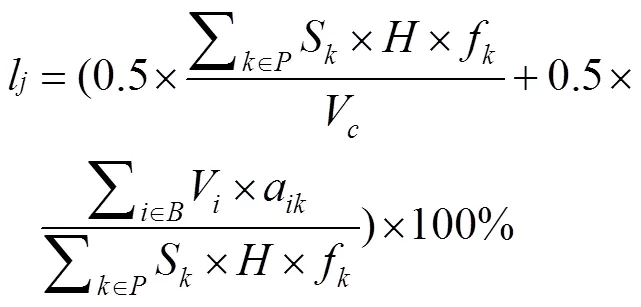
式中：=1, 2。

表2 测试算例参数

Tab.2 Parameters of experimental case

表3 小规模算例数据对比

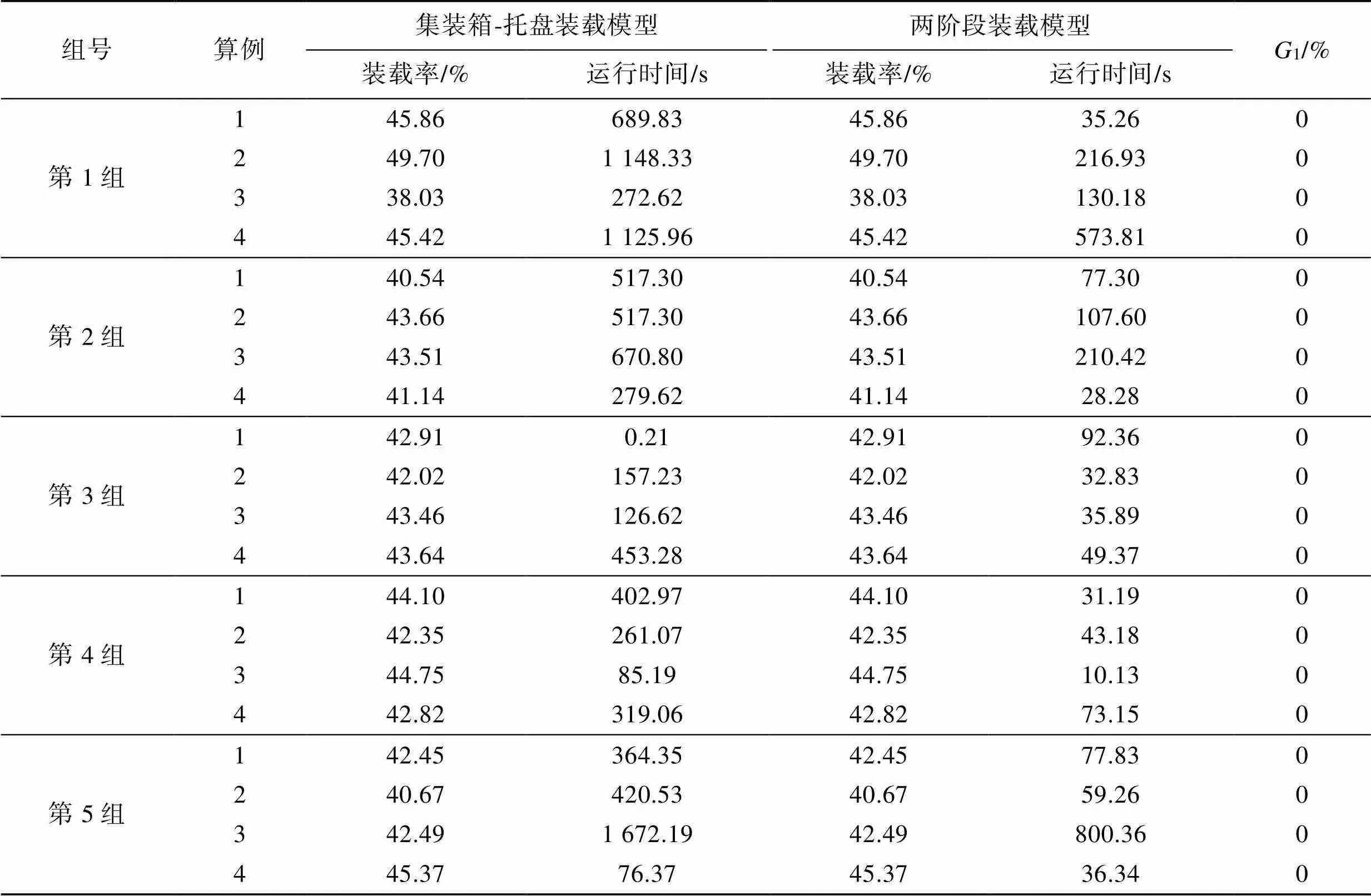
Tab.3 Comparison of small-scale experimental case data

表3列出了集装箱-托盘装载模型、两阶段装载模型对5组小规模算例进行计算的结果（装载率和运行时间）。从装载率角度来看，集装箱-托盘装载模型与两阶段装载模型在一定时间内实现了精确求解，获得了最优解，1均为0，验证了2个模型的正确性及有效性。

将2个模型对5组小规模算例的平均运行时间绘制成折线图，如图4所示。由图4可知，两阶段装载模型的折线斜率相对变化幅度不大，鲁棒性相对较好，且对5组算例的平均运行时间相对较少，总平均运行时间仅为109.41 s，而集装箱-托盘装载模型的平均运行时间为473.87 s。可以看出相较于集装箱-托盘装载模型，两阶段装载模型在较短时间内获得了最优解，收敛性好。究其原因，两阶段装载模型在第1阶段中确定了托盘装载数量，减少了第2阶段解的搜索空间，从而收敛性相对较好，提高了求解速度，减少了运行时间。

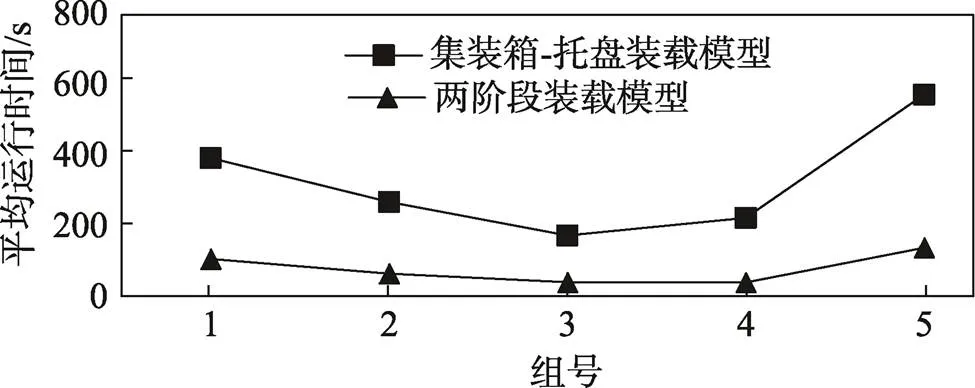
图4 5组小规模算例的平均运行时间折线图

2.3 大规模算例

表4 大规模算例数据对比

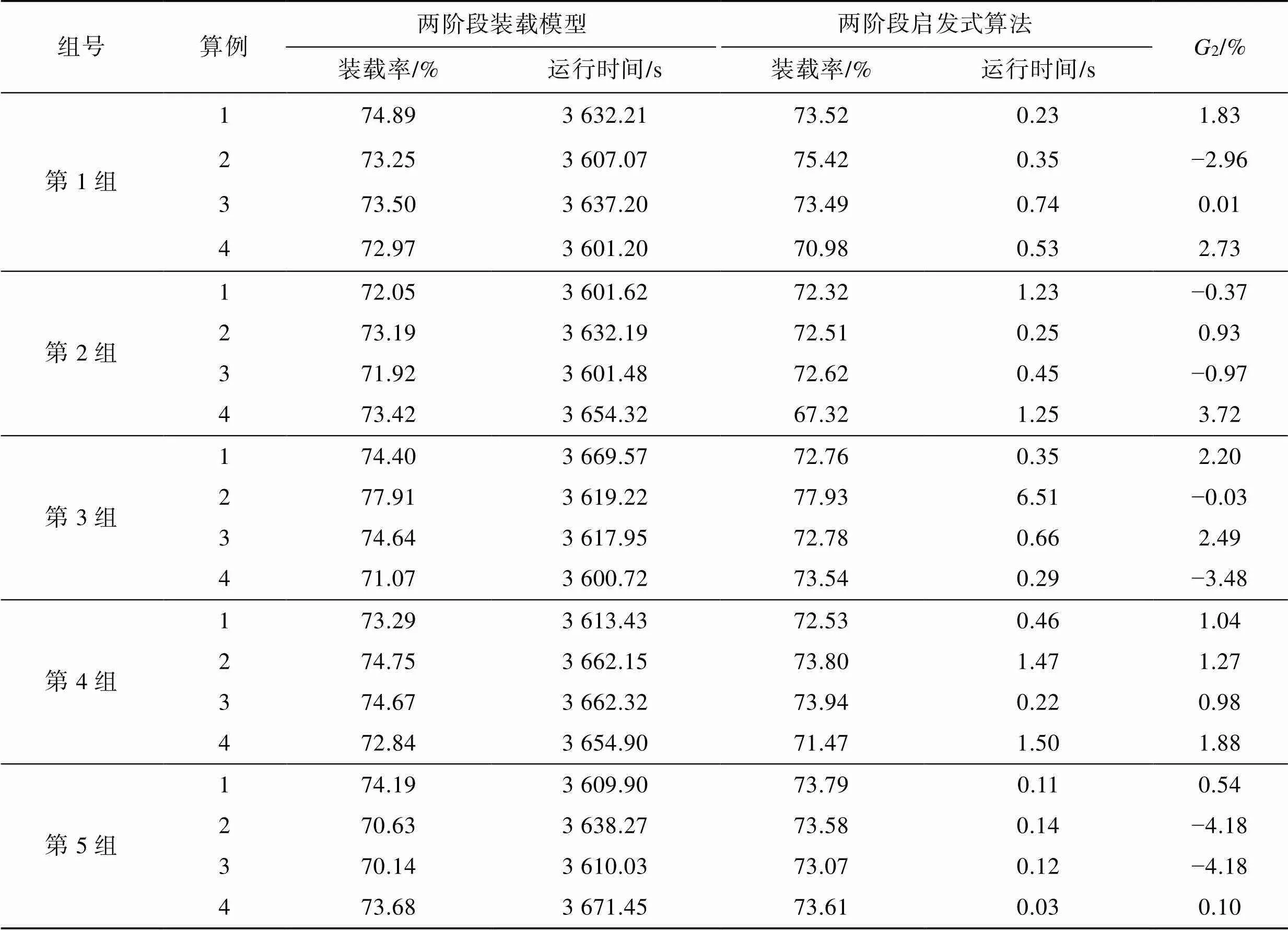
Tab.4 Comparison of large-scale experimental case data

对表4中5组实验的2值按照升序排列，如图5所示。由图5可知，在5组实验中，折线图的上下界为[−5%，5%]，斜率增长速度相对较小，说明该算法求解的装载率与下界值相差不大，鲁棒性强。全部实验中，2最大值为3.72%，最小值为−4.18%，平均值为−0.5%，说明两阶段启发式算法的装载率与下界值相差不大。在保证了产品装载垛形稳定的约束条件下，两阶段启发式算法获得了理想的装载方案。

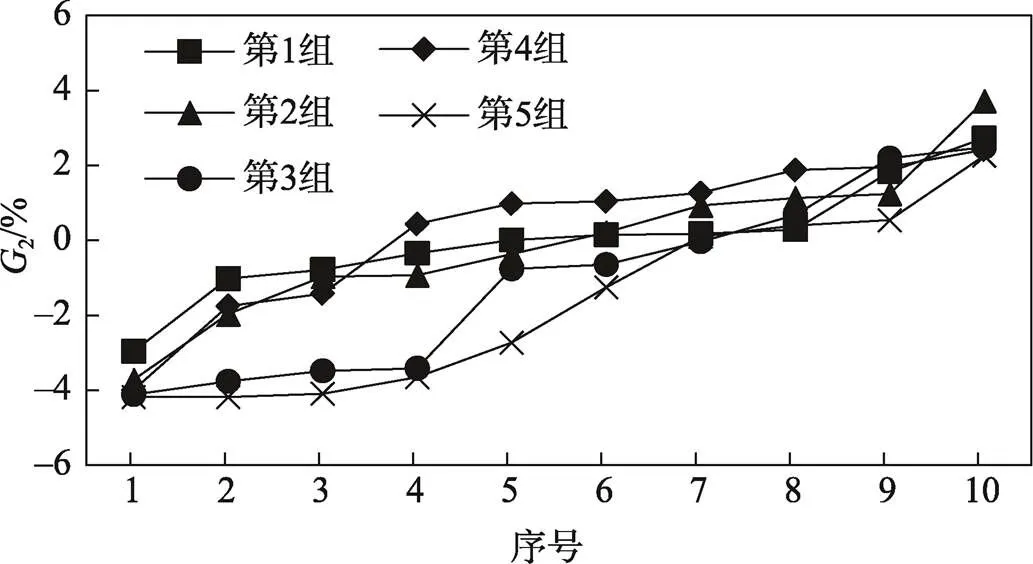
图5 5组大规模算例实验的G2值折线图

从运行时间来看，两阶段装载模型的平均运行时间为3 636.02 s，而两阶段启发式算法的平均运行时间仅为1.82 s，运行时间差距相对较大，在较短的时间内便获得了理想的装载方案。究其原因，该算法在第2阶段将三维托盘装载问题转化为二维托盘装载问题，极大地缩小了解的搜索空间，在顶部剩余空间中按照体积大小顺序装入产品，提高了装载率，收敛性好；且在50个算例实验中，两阶段启发式算法的运行时间标准差为2.14，平均标准差仅为1.17，说明算法的稳定性较好。

从以上分析结果可以看出，在大规模算例实验中，两阶段启发式算法所产生的产品装载方案既保证了产品装载的垛型稳定，又具有高的空间利用率，避免产生浪费；两阶段启发式算法能在较短的时间内得到好的装载方案，鲁棒性强，实用性好，能为工厂产品的托盘打包及装箱提供参考。

3 结语

将工厂产品的托盘打包及装箱问题进行统筹优化，建立了以产品装载体积最大化为目标的集装箱-托盘装载模型，并将该问题分解为二维集装箱装载和三维托盘装载2个子问题，针对2个子问题建立了两阶段装载模型进行求解。当产品数量过多导致模型难以求解时，建立两阶段启发式算法求解。采用2种规模大小的算例对模型和算法进行了测试，验证了模型及算法的有效性。本文的研究能够为工厂产品的托盘打包及装箱问题提供满意的解决方案，从而减少空间浪费，提高经济效益。但本文所提的模型及算法还有一些不足之处，随着产品数量的增加，模型及算法复杂度更高，计算时间更长等；本文只考虑在集装箱底部装载托盘，未考虑托盘承重问题。因此，将来的工作需进一步优化算法，提高计算速度，同时将考虑更多的实际应用场景和约束条件，以提出更好、更适用的解决方案。

[1] 尚正阳, 黄秋妍, 康正阳, 等. 一刀切约束下的二维装箱问题高效求解算法[J]. 包装工程, 2021, 42(7): 231-238.

SHANG Zheng-yang, HUANG Qiu-yan, KANG Zheng-yang, et al. Efficient Heuristic Algorithm for the Two-Dimensional Guillotine Rectangular Bin Packing Problem[J]. Packaging Engineering, 2021, 42(7): 231-238.

[2] ARAYA I, MOYANO M, SANCHEZ C. A Beam Search Algorithm for the Biobjective Container Loading Problem[J]. European Journal of Operational Research, 2020, 286(2): 417-431.

[3] 刘胜, 沈大勇, 商秀芹, 等. 求解三维装箱问题的多层树搜索算法[J]. 自动化学报, 2020, 46(6): 1178-1187.

LIU Sheng, SHEN Da-yong, SHANG Xiu-qin, et al. A Multi-Level Tree Search Algorithm for Three Dimensional Container Loading Problem[J]. Acta Automatica Sinica, 2020, 46(6): 1178-1187.

[4] 刘胜, 朱凤华, 吕宜生, 等. 求解三维装箱问题的启发式正交二叉树搜索算法[J]. 计算机学报, 2015, 38(8): 1530-1543.

LIU Sheng, ZHU Feng-hua, LYU Yi-sheng, et al. A Heuristic Orthogonal Binary Tree Search Algorithm for Three Dimensional Container Loading Problem[J]. Chinese Journal of Computers, 2015, 38(8): 1530-1543.

[5] BAYRAKTAR T, ERSÖZ F, KUBAT C. Effects of Memory and Genetic Operators on Artificial Bee Colony Algorithm for Single Container Loading Problem[J]. Applied Soft Computing Journal, 2021, 108: 107462.

[6] 张长勇, 翟一鸣. 基于改进遗传算法的航空集装箱装载问题研究[J]. 北京航空航天大学学报, 2021, 47(7): 1345-1352.

ZHANG Chang-yong, ZHAI Yi-ming. Air Container Loading Based on Improved Genetic Algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(7): 1345-1352.

[7] 王帅, 洪振宇. 基于强化学习的机场行李装箱优化方法[J]. 包装工程, 2022, 43(3): 257-263.

WANG Shuai, HONG Zhen-yu. Optimization Method of Baggage Packing in Airport Based on Reinforcement Learning[J]. Packaging Engineering, 2022, 43(3): 257-263.

[8] 吕雪菊, 倪静. 基于自适应空间划分策略的三维装箱问题[J]. 系统工程, 2020, 38(4): 95-102.

LYU Xue-ju, NI Jing. Three Dimensional Container Loading Problem Based on Adaptive Spatial Partition Strategy[J]. Systems Engineering, 2020, 38(4): 95-102.

[9] ALJUHANI D, PAPAGEORGIOU L. Improved Layout Structure with Complexity Measures for the Manufacturer's Pallet Loading Problem (MPLP) Using a Block Approach[J]. Journal of Industrial Engineering and Management, 2021, 14(2): 231-249.

[10] DELL'AMICO M, MAGNANI M. Solving a Real-Life Distributor's Pallet Loading Problem[J]. Mathematical and Computational Applications, 2021, 26(3): 53-63.

[11] PISINGER D, SIGURD M. The Two-Dimensional Bin Packing Problem with Variable Bin Sizes and Costs[J]. Discrete Optimization, 2005, 2(2): 154-167.

[12] CUI Y P, CUI Y D, TANG T B. Sequential Heuristic for the Two-Dimensional Bin-Packing Problem[J]. European Journal of Operational Research, 2015, 240(1): 43-53.

[13] 宋卫生, 薛阳. 托盘装载优化设计系统的开发[J]. 包装工程, 2021, 42(13): 205-211.

SONG Wei-sheng, XUE Yang. Development of Pallet Loading Optimization Design System[J]. Packaging Engineering, 2021, 42(13): 205-211.

[14] SHENG Liu, ZHAO Hong-xia, DONG Xi-song, et al. A Heuristic Algorithm for Container Loading of Pallets with Infill Boxes[J]. European Journal of Operational Research, 2016, 252(3): 728-736.

[15] ALONSO M T, ALVAREZ-VALDES R, PARREÑO F. A GRASP Algorithm for Multi Container Loading Problems with Practical Constraints[J]. 4OR, 2020, 18(4): 49-72.

[16] ALONSO M T, ALVAREZ-VALDES R, IORI M, et al. Mathematical Models for Multi Container Loading Problems with Practical Constraints[J]. Computers & Industrial Engineering, 2018, 127: 722-733.

[17] SHI Yong, ZHOU Yan-jie, BOUDOUH T, et al. A Lexicographic-Based Two-Stage Algorithm for Vehicle Routing Problem with Simultaneous Pickup-Delivery and Time Window[J]. Engineering Applications of Artificial Intelligence, 2020, 95(2): 103901.

Pallet Packing and Container Loading of Factory Products Based on Mixed Integer Programming Approach

ZHANG Jing-rong, HE Zhan-wen, ZHOU Yan-jie*, LI Yu-min

(School of Management, Zhengzhou University, Zhengzhou 450001, China)

The work aims to propose a method to optimize the layout of products on pallets and the layout of pallets and products in containers to maximize container space utilization, thus solving the problem in pallet packing and container loading of factory products. A mixed integer programming model was developed to optimize the volume of the loaded product under realistic constraints. Due to the complexity of the problem, the studied problem was divided into two sub-problems and a two-stage loading model was established for solution. In the first stage, a two-dimensional container loading model was established to determine the plane layout of pallets on the bottom of containers. In the second stage, a three-dimensional pallet loading model was established to determine the 3D layout of products on the pallet. In view of that accurate solution was time-consuming, a two-stage heuristic algorithm was designed to solve the two sub-problems. To verify the effectiveness of the model and algorithm, two groups of examples with different sizes were adopted. The results showed that the average difference of loading rate was 0 and −0.5% in small and large-scale experimental cases, respectively, but the calculation time was quite different. The model and algorithm proposed could obtain the optimal solution or approximate optimal solution in a reasonable time. This study can provide a fast and efficient solution for pallet packing and container loading of factory products.

container; loading; pallet packing;factory products; mixed integer programming; heuristic algorithm

U294.3

A

1001-3563(2023)17-0143-09

10.19554/j.cnki.1001-3563.2023.17.017

2022-12-02

国家自然科学基金资助项目（72201252）；河南省社科规划决策咨询项目（2022JC10）；河南省高校智库研究项目（2023ZKYJ21）

责任编辑：曾钰婵