个性化角接触球轴承的优化设计方法

2023-09-13韩泽光廖小萱郝瑞琴白晓天

沈阳建筑大学学报（自然科学版） 2023年4期

韩泽光,廖小萱,郝瑞琴,白晓天

(沈阳建筑大学机械工程学院,辽宁沈阳 110168)

滚动轴承是机械设备中重要的基础元件,主要用来承受载荷和传递动力,在重型机械和航空航天中广泛应用[1]。如今,高速重载的机械设备对轴承的工作性能和使用寿命有了更高的要求,而轴承内部未标准化的结构参数与其工作表现是息息相关的。张腾等[2]建立以轴承疲劳寿命最长为目标的优化模型来改变轴承的内圈挡边根部厚度、外圈最小内径和公称接触角,得出锥角取28°30′时承载能力最大;王德伦等[3]以双列圆锥滚子轴承为研究对象,建立了体积最小和寿命最长的优化数学模型,求解出轴承内径、外径、座圈宽度等几何结构参数的最优值;D.Eugeniv[4]进行了最大额定寿命的优化设计,开发了相应优化程序,得出优化接触角和节距比可以最大限度地延长额定寿命;吕志鹏等[5]以谐波减速器中的柔轮支承轴承为研究对象,建立了轴承额定动载荷最大和磨损寿命最长目标下的优化模型,利用MATLAB和ISIGHT联合优化求解,结果表明,滚珠直径对目标的影响最大;罗天宇等[6]以滚动体直径、滚动体个数和节圆直径作为设计变量,建立了角接触球轴承刚度最大或额定动载荷最大目标下的优化数学模型并求解,数据表明不同的优化目标导致了结果的差异性;T.Rajiv等[7]以动态承载能力最大、弹性流体动力最小、油膜厚度最大及轴承温度最小为目标对球面滚子轴承进行了优化设计,经遗传算法得到轴承寿命明显提高的最优结构参数;张静静等[8]基于轴承寿命为目标对其球数、球径、垫片角、内外圈沟曲率半径系数及径向游隙进行了优化设计,采取正交试验法得到结构参数对轴承寿命的影响规律;汪久根等[9]以双列角接触球轴承的钢球数、钢球直径、内外滚道沟曲率半径系数以及节圆直径为设计变量,进行了额定动载荷和额定静载荷最大目标下优化设计。上述研究中未曾考虑高速运转情况下润滑对轴承性能的影响,优化功能单一,难以支撑轴承产品的个性化设计。

基于此,笔者提出一种保证轴承承载能力最大和润滑性能最好的多目标非线性约束问题的角接触球轴承解决方案,通过算例验证其有效性和可靠性,以满足用户多样性和个性化需求,丰富轴承的制造样本。

1 优化数学模型

1.1 设计变量

角接触球轴承的几何尺寸参数如图1所示。在《滚动轴承代号方法》(GB/T 272—2017)中对轴承内部结构相关的轴承节圆直径Dm、滚动体直径Db、滚动体个数Z、内外滚道沟曲率半径系数fi、fo没有进行标准化,这些参数变化对轴承性能有着重要影响,因此选取上述五个参数作为设计变量,同时为保证优化过程能更好地满足工程实际要求,增加滚动体最大直径控制系数kDmax,滚动体最小直径控制系数kDmin,轴承外环强度控制系数ε,轴承运转控制系数e,轴承宽度控制系数ξ等与约束条件相关的变量控制系数[10]作为设计变量,因此角接触球轴承的优化数学模型的设计变量为

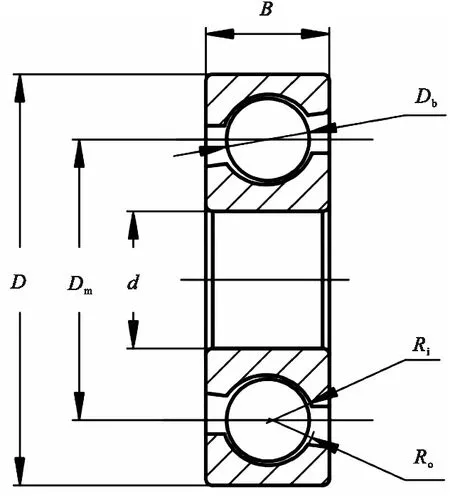
图1 角接触球轴承几何尺寸参数Fig.1 The geometric dimension parameters of angular contact ball bearings

X=[Dm,Db,Z,fi,fo,kDmin,kDmax,ε,e,ξ]T=

[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10]T.

(1)

1.2 目标函数

1.2.1 基本额定静载荷最大

滚动轴承在低速条件下工作时,基本额定静载荷越大,说明轴承的静强度越大,因此,为提高低速工况下轴承的工作性能,角接触球轴承的基本额定静载荷CS的目标函数为

maxf1(X)=min(CS,内,CS,外).

(2)

式中:CS,内,CS,外分别是内、外圈的基本额定静载荷。

(3)

(4)

1.2.2 基本额定动载荷最大

基本额定动载荷是轴承中、高转速工况下疲劳寿命的重要影响因素,此处采用国际上通用的Lundberg-Palmgren式[11]计算,因此对应的目标函数表达式为

(5)

1.2.3 最小油膜厚度最大

高转速条件下工作的轴承必须考虑油膜厚度对其润滑的影响,结合国际上通用的Hamrock和Dowson提出的轴承油膜厚度计算公式,导出的目标函数为

maxf3(X)=min(Hmin内,Hmin,外).

(6)

式中:Hmin,内、Hmin,外分别为内、外圈处的最小油膜厚度。

(7)

(8)

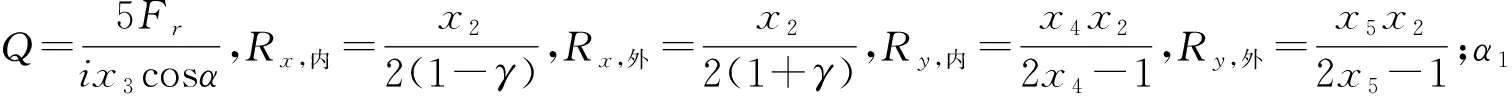
1.3 约束条件

1.3.1 滚动体的个数

为了确保滚动体能便利地装配在内、外圈之间,则滚动体直径和个数的约束条件为

(9)

1.3.2 滚动体直径受到轴承的内外径的限制

为保证合理装配,滚动体直径应由限制参数kDmax,kDmin限定,相应的约束条件为

g2(X)=2x2-x6(D-d)≥0.

(10)

g3(X)=x7(D-d)-x2≥0.

(11)

1.3.3 轴承的节圆直径

为保证轴承中滚动体运转良好,轴承的节圆直径与内外径之间的平均直径不能相差太大,引入限制参数e确定的约束条件为

g4(X)=x1-(0.5-x9)(D+d)≥0.

(12)

g5(X)=(0.5+x9)(D+d)-x1≥0.

(13)

1.3.4 滚动体直径

滚动体直径受到轴承宽度的限制,则相应的约束条件为

g6(X)=x10B-x2≥0.

(14)

1.3.5 轴承外滚道处的套圈厚度

为保证轴承的强度,轴承外滚道处的套圈厚度不应小于εDb,相应的约束条件为

g7(X)=0.5(D-x1-x2)-x8x2≥0.

(15)

1.3.6 内外滚道曲率半径系数

为保证轴承的动态承载能力,内外滚道曲率半径系数不应小于0.515,相应的约束条件为

g8(X)=x4-0.515≥0.

(16)

g9(X)=x5-0.515≥0.

(17)

2 优化模型的求解方法和方案排序

2.1 优化算法选择

上述优化数学模型属于3个目标函数、9个约束条件的非线性优化问题,为了避免优化算法需要求导和易于陷入局部最优的不足,选用运行速度快,解集收敛性好的快速非支配排序算法NSGA-Ⅱ作为求解算法。

2.2 优化结果的工程化处理

2.2.1 处理原则

通过上述算法可以得到大量的pareto实数解,且精确到小数点后四位有效数字,数据差异度小,不便于工程应用实施,为此需要对设计结果进行工程化处理,具体处理原则:①滚动体的个数取整;②小数点后保留两位有效数字;③数值非常接近的解仅保留1个,其余剔除。

2.2.2 方案评价

采用熵权-TOPSIS法进行方案评价。熵权法计算设计变量和目标函数的权重,TOPSIS法完成方案的综合评价,保证了权重计算结果相对客观准确,决策层次分明,为滚动轴承产品的多样化和个性化提供保证。

熵权法是一种客观赋权的数学评价方法[12],信息熵值越小,说明该指标对综合评价的权重也就越大。

多目标多变量问题中计算权重原理:假设将要评价的方案数为n,每个方案有m(设计变量与目标函数的数目)个指标,xij表示为第i个方案的第j个指标的数值(i=1,2,…,n;j=1,2,…,m)。

(1)指标归一化处理

为了消除各个指标之间的量纲差异,将指标的绝对数值转化为相对数值,实现各项不同质指标值的同质化。指标分为正向和负向,正向指标值越高,目标值越好;负向指标值越高,目标值越差。正向指标和负向指标分别由式(18)和式(19)计算。

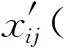
(18)

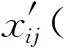
(19)

(2)计算指标在方案中的比重

第j个指标在第i个方案值占该指标的比重为

(20)

(3)计算指标的熵值

第j个指标的熵值为

(21)

(4)计算信息熵冗余度

dj=1-ej.

(22)

(5)计算各个指标的权重

(23)

TOPSIS 法是常用的一种多目标决策方法,该方法是借助评价方案与方案正负理想解的相对距离确定的贴近度对其进行排序[13],方案相对贴近度越大,说明该方案越好。TOPSIS法在角接触球轴承方案排序的原理详述如下:

①构建方案和指标矩阵An×m

矩阵A中元素aij为(i=1,2,…,n;j=1,2,…,m)第i个方案的第j个指标的数值。

(24)

②矩阵A正向化处理为矩阵X

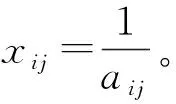
(25)

③矩阵X转化为标准化Z

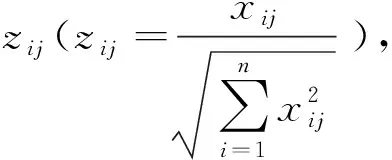
(26)

由此可确定最优方案Z+(Z中每列元素的最大值构成)和最劣方案Z-(Z中每列元素的最小值构成),即

(27)

(28)

④计算各评价方案的贴近度Ci

(29)

其中,0≤Ci≤1,当Ci越接近1时,说明评价对象越优秀。根据计算得到的Ci值大小来进行排序,得到各个方案的评价排序结果。

3 工程算例

3.1 设计条件

选用型号为7200AC角接触球轴承,其外径为D=30 mm,内径为d=10 mm,轴承宽度B=9 mm,设定接触角α=25°,轴承列数i=1,内圈转速ni=5 000r/min,常压下润滑油的动力黏度为ηo=0.02 Pa·s,黏度系数为α1=10-8,杨氏弹性模量为E0=2.25×1011Pa,轴承受到的径向载荷为Fr=5 000 N。

3.2 设计变量的取值范围

由文献[14]可知设计变量的取值范围分别为:x1∈[0.5(D+d),0.6(D+d)],x2∈[0.15(D-d),0.35(D-d)],x4∈[0.515,0.6],x5∈[0.515,0.6],x6∈[0.4,0.5],x7∈[0.6,0.7],x8∈[0.3,0.35],x9∈[0.03,0.08],x10∈[0.7,0.85]。

3.3 优化结果

根据以往NSGA-Ⅱ优化算法使用经验和此次优化设计的需要,此次优化设计设定种群大小300个,最大代数300代,交叉概率0.8,变异概率0.08,交叉分布指数为20,变异分布指数为10,随机种子为0.5。优化后得到图2所示的300个Pareto解,两两目标之间的分析如图3、图4所示。

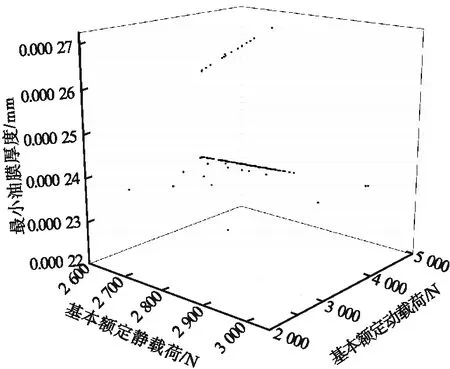
图2 Pareto解Fig.2 The Pareto solution

图3 目标1与目标2的分析图Fig.3 The analysis diagram of goal 1 and goal 2

图4 目标1与目标3的分析图Fig.4 The analysis diagram of goal 1 and goal 3

由图2～图4可知,NSGA-Ⅱ优化算法与NSGA算法相比求解多个非线性约束组成的多目标函数可以快速获得大量的非支配解,且这些解组成的Pareto前沿面更加柔顺。因此,以此方法优化可确保设计出的滚动轴承综合性能俱佳。

3.4 结果分析

按照前述数据工程化原则,在Pareto前沿面上获得了10组优秀且最具实用性的多目标Pareto解方案,如表1所示。经相应的排序算法程序运行计算得到方案的评价结果如表2所示,表2中对比的标准值是文献[14]中相对应的数据。

表1 多目标Pareto解方案Table 1 The Pareto solution of multi-objective

表2 熵权-TOPSIS法的方案评价结果Table 2 The evaluation results of entropy-TOPSIS method

由表可知,不同的几何尺寸对轴承的性能影响差异较大,高速重载下的轴承主要保证轴承的基本额定动载荷最大和最小油膜厚度最小,以确保其疲劳寿命更长,因此推荐使用方案3、8;低速重载条件下的轴承,要求基本额定静载荷最大,推荐用方案1、3、8;低速轻载条件下工作的轴承,对基本额定静载荷和基本额定动载荷要求不高,推荐用方案4、7、9;高速轻载条件下工作的轴承,基本额定动载荷要适中以确保寿命长,基本额定静载荷要求不高,推荐用方案2、5、6、10。从工程实际来看,多样化的数据方案丰富了滚动轴承的标准系列,而个性化评价为轴承生产提供了更加合适的内部尺寸方案,这样不仅充分发挥了轴承性能,而且降低了其使用成本。