基坑开挖对邻近建筑物天然地基变形影响及控制措施

2023-09-13韩健勇王庆海赵明城崔中全

沈阳建筑大学学报（自然科学版） 2023年4期

韩健勇,王庆海,赵明城,崔中全,柏谦

(1.山东建筑大学土木工程学院,山东济南 250101;2.山东建筑大学建筑结构加固改造与地下空间工程教育部重点实验室,山东济南 250101;3.中建八局第一建设有限公司,山东济南 250100;4.济南中央商务区投资建设集团有限公司,山东济南 250014;5.东北大学资源与土木工程学院,辽宁沈阳 110004)

天然地基是指在自然状态下就能够满足基础全部荷载要求、无需进行人工处理的地基。随着建筑材料的不断更新和发展,施工技术的不断进步,基坑施工邻近建筑物天然地基的工况也会越来越多。明确砂土地层基坑开挖引起的邻近建筑物天然地基变形规律和对天然地基变形的有效控制措施,对于保障基坑及周边建筑群安全和稳定至关重要。

目前,已经有很多学者对基坑开挖引起的建筑物沉降和围护结构变形展开了研究。韩健勇等[1]基于现场实际监测数据及数值计算结果,对基坑开挖引起的既有建筑物的变形特性和基坑围护结构进行了研究。邓旭等[2]结合天津实际深基坑工程,研究了基坑开挖对基坑围护结构和邻近结构的影响。范凡等[3]将数值模拟计算与工程经验相结合,研究了坑外土体竖向位移随基坑开挖深度的变化规律。陈阳等[4]基于某基坑工程的现场实测数据,对排桩内支撑基坑支护体系中的桩顶水平位移、桩体侧向位移以及基坑周边土体沉降量进行了深入研究。李志[5]基于北京某基坑工程,通过理论设计、模型试验和数值模拟三者相结合的方式研究了钢管桩基坑支护的位移、应力、变形及对基坑稳定性的影响,对钢管桩代替钻孔灌注桩的可行性进行了研究。晋霞[6]通过模型试验分别模拟了三种基坑开挖工况,得到了在基坑开挖过程中支护结构的受力变形和周围建筑基础沉降之间的相互作用和影响规律。王琳等[7-8]基于数值模拟研究了不同施工方法、施工参数下基坑开挖对周围环境的影响。E.Khalid[9]通过现场监测分析了基坑开挖对邻近建筑物沉降的影响。S.Y.Fan[10]通过数值模拟研究了大型基坑开挖对围护结构水平位移的影响。Y.Tan等[11-12]通过现场监测和数值模拟,研究了大型基坑开挖对基坑围护结构受力及坑外土体变形的影响。

在基坑与建筑物之间布置隔离桩是一种控制变形的方法。关于隔离桩方面的研究,郑刚等[13]在工程实测数据的基础上,采用有限元方法对隔离桩的作用机制进行了参数分析,并研究了隔离桩对土体深层位移及对隧道位移的控制机制。翟杰群等[14]对隔离桩的作用机理和结构形式进行了研究,并给出了隔离桩桩长、隔离桩结构形式等参数对隔离桩控制变形的影响规律。曾晓鑫等[15]采用ABAQUS有限元软件对不同隔离桩间距下隧道的位移进行了分析。纪新博等[16]针对某采用隔离桩隔离的工程进行了正交有限元法优化研究,得出隔离桩的打设和注浆对变形和内力有一定的控制作用。

上述研究多集中在围护结构变形和建筑物沉降方面,而对基坑开挖引起的邻近建筑物下方天然地基的变形研究较少。另外,当前的研究表明,设置隔离桩可以较好地控制开挖引起的地基变形,但对于隔离桩的相关参数研究还不够全面。基于此,笔者结合某基坑工程,首先进行不同工况下基坑开挖模型试验,研究基坑开挖对天然地基变形的影响,然后基于室内试验建立数值模型,分析隔离桩间距和隔离桩埋深等参数对天然地基变形的控制效果。研究表明,基坑开挖会使建筑物天然地基竖向位移超过报警值,设置合适的隔离桩参数可以显著减少开挖引起的天然地基变形。

1 试验

1.1 试验装置

试验原理如图1所示。

利用位移传感器监测整个试验过程中的竖向位移,并通过数据采集仪对数据进行收集。试验在长×宽×高为900 mm×750 mm×600 mm、厚度为10 mm的模型箱内进行,模型箱材质为有机玻璃,具有较好的透明性。为减少地基材料与模型箱内部侧壁的摩擦,在模型箱内部四周贴上0.04 mm的聚乙烯薄膜。

模型箱尺寸如图2所示。依托基坑工程开挖深度为7.5 m,开挖长度为22.5 m,开挖宽度为9 m,考虑实际工况和室内试验场地限制,试验的几何相似比取30,因此试验中基坑开挖深度为250 mm,开挖长度为750 mm,开挖宽度为300 mm。模型箱的长度是基坑开挖深度的三倍以上,满足边界条件要求。

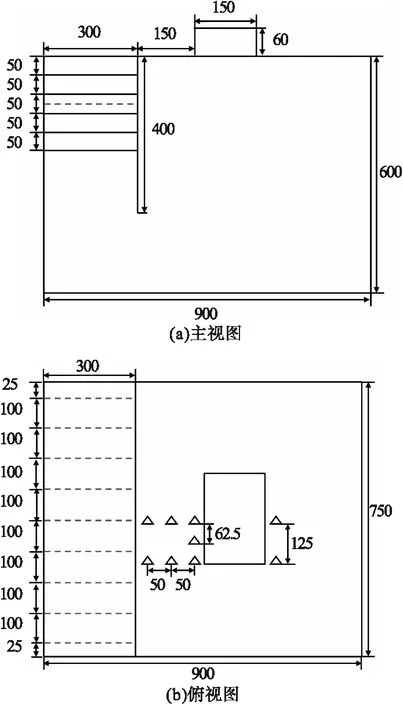
图2 模型箱尺寸Fig.2 Model tank size

1.2 模型材料

依托工程原型围护结构为15根直径1.5 m、长度9 m、间距1.5 m的C30混凝土灌注桩。基坑围护结构主要发挥抗弯作用,根据等效刚度替代法对原型围护结构进行替换[17],根据相似定理可知模型中围护结构的抗弯刚度为

(1)

式中:Em为模型弹性模量;Im为模型惯性矩;Ep为原型弹性模量;Ip为原型惯性矩;CL为长度相似比。

根据式(1)得出模型围护结构的抗弯刚度为4.602×10-5kN·m2,为防止试验中围护结构之间漏土,选用薄铝板代替原型灌注桩,其弹性模量约为68 GPa。根据矩形惯性矩公式和模型箱尺寸求出铝板长×宽×厚为750 mm×400 mm×0.5 mm,厚度约为0.47 mm,为便于加工,铝板的厚度选为0.5 mm。

依托工程内支撑原型为直径609 mm、厚度16 mm、长度9 m、间距3 m的钢支撑。内支撑主要发挥抗压作用,根据等效刚度替代法对原型内支撑进行替换,根据相似定理可知模型中围护结构的抗压刚度为

(2)

式中:Am为模型截面积;Ap为原型截面积。

根据式(2)得出模型内支撑的抗压刚度为2.428×102kN,选用PVC管作为相似材料,其弹性模量约为3 GPa。根据圆环面积公式和模型箱尺寸求出PVC管的直径为16 mm,厚度为2 mm,长度为0.3 m,间距为0.1 m。试验模型中采用钢板模拟建筑物基础,一块钢板的附加荷载为4.71 kPa,根据相似原理,实际作用在地基上的附加荷载为141.3 kPa,相当于底面长×宽为7.5 m×4.5 m的10层框架结构作用在地基上。

选取彰武砂作为模型土进行基坑开挖模型试验,彰武砂属大林矿系主矿脉的天然风积砂,其粒径均匀符合试验要求。通过系列土工试验得到模型土的力学参数见表1。

表1 模型土力学参数Table 1 Mechanical parameters of model soil

N.K.Ovesen[18]通过试验得出,当基础直径与砂土平均粒径之比大于30时,土体材料不缩制不会对地基承载特性有较大影响,此时可以选用原型土料进行试验。模型试验中与土体接触的钢块最小宽度为150 mm,与模型土平均粒径比值为746,符合要求。采用砂雨法分层制备性能稳定的人工模型地层,并在试验前进行标定。模型试验中落砂高度取1.1 m,由此制备的土层相对密实度约为0.6。

1.3 试验工况及方案

试验共分4组工况,建筑物采用4块长×宽×高为250 mm×150 mm×60 mm的钢板模拟,通过增加钢板数量来模拟不同的建筑物附加荷载。在钢板底部贴上砂纸增加其与模型土的摩擦力,以便更好地模拟实际中砂土与上覆结构的相互作用。

根据《建筑基坑工程监测技术规范》(GB 50497—2009)可知,基坑周边地表竖向位移监测点宜按监测剖面布置在坑边中部,且监测剖面与坑边垂直,建筑物周围地表竖向位移的报警值为10～60 mm,文中取30 mm。根据相似理论可知,试验中地表竖向位移的报警值为1 mm。采用量程为50 mm的位移传感器并结合3 816 N数据采集仪测定建筑物基础周围竖向位移,试验中位移传感器空间位置分布及试验装置见图3。位移传感器1和位移传感器5测定靠近基坑的地表竖向位移,位移传感器2和位移传感器6测定基坑与建筑物基础之间的地表竖向位移,位移传感器3～4、7～9用来测定建筑物基础周边的地表竖向位移。

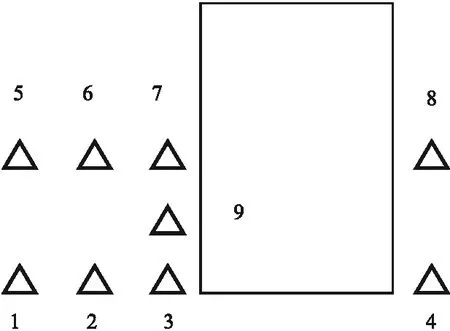
图3 位移传感器布置图Fig.3 Layout of displacement sensors

每组试验均分五步开挖,每步开挖深度50 mm,每层开挖土下方放置一张透明薄膜,便于标记和取土。开挖前记录位移传感器初始示数,采用取土设备开挖至第一层透明薄膜,待位移传感器示数稳定后记录此时位移传感器示数;继续开挖至第二层透明薄膜,待位移传感器示数稳定后记录此时位移传感器示数;在开挖第三层土体的同时布置PVC管,将其固定在铝板和模型箱之间。PVC管位于100 mm标高处,继续开挖至第五层透明薄膜,试验结束并记录位移传感器数据。

2 结果与分析

提取步骤一(基坑开挖深度0.05 m)、步骤二(基坑开挖深度0.1 m)、步骤三(基坑开挖深度0.15 m)、步骤四(基坑开挖深度0.2 m)和步骤五(基坑开挖深度0.25 m)的位移传感器数据。相同附加荷载条件下各测点地表竖向位移随基坑开挖深度变化曲线如图4所示。

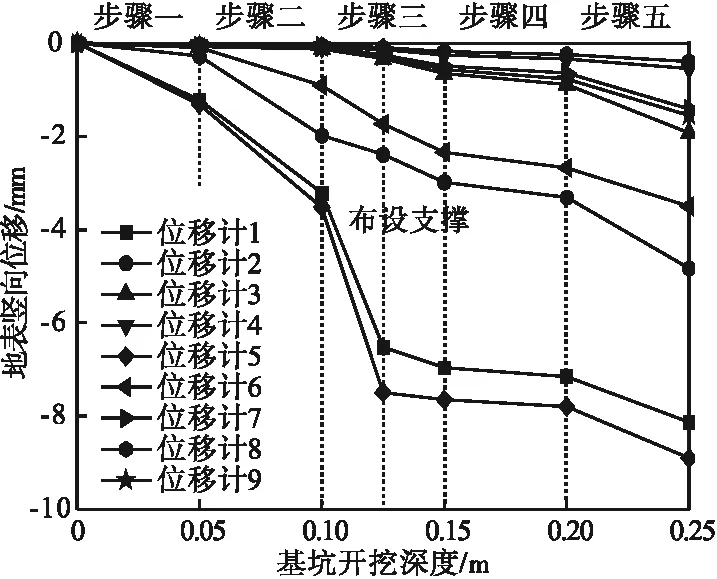
图4 地表竖向位移随基坑开挖深度变化曲线Fig.4 Variation of vertical surface displacements with excavation depth

由图4可知,随着基坑开挖深度逐渐增加,各位移传感器的示数逐渐增大。其中位移传感器1和位移传感器5的示数变化幅度最大,这是由于这两个测点靠近基坑开挖区,所受的扰动最大。位移传感器2和位移传感器6处于基坑与建筑物基础之间,在整个基坑开挖过程中,位移传感器2的示数均大于位移传感器6的示数,笔者认为这是由于建筑物基础的存在引起了周围土体的隆起,进而抵消了一部分基坑开挖引起的竖向位移,且建筑物荷载对基础四周土体的影响小于对基础中部土体的影响。位移传感器3、7、9的变化趋势基本相同,位移传感器3的示数最大,位移传感器7的示数最小。

位移传感器3～4、7～9测定的是建筑物基础周围天然地基的沉降。当放置一块钢板时,随着基坑开挖深度的增加,位移传感器4和位移传感器8的示数均未超过报警值。基坑开挖深度大于0.2 m时,位移传感器3、7、9示数均超过报警值,且位移传感器3的示数与位移传感器7相比增大了26.56%,与位移传感器4相比增大了71.87%。当放置两块钢板时,位移传感器4和位移传感器8的示数均未超过报警值,位移传感器4的示数与位移传感器8相比增大了19.27%。基坑开挖深度大于0.1 m时,位移传感器3、7、9示数均超过报警值,位移传感器3的示数与位移传感器7相比增大了25.31%,与位移传感器4相比增大了64.9%。

当放置三块钢板时,位移传感器4的示数在基坑开挖深度为0.25 m时超过报警值,位移传感器8的示数未超过报警值,位移传感器4的示数与位移传感器8相比增大了34.37%。基坑开挖深度大于0.1 m时,位移传感器3、7、9示数均超过报警值,位移传感器3的示数与位移传感器7相比增大了23.52%,与位移传感器4相比增大了52.94%;位移传感器7示数与位移传感器8相比增大了59.61%。当放置四块钢板时,位移传感器4和位移传感器8均超过报警值,且位移传感器4的示数与位移传感器8相比增大了36.86%。基坑开挖深度大于0.1 m时,位移传感器3、7、9示数均超过报警值,位移传感器3的示数与位移传感器7相比增大了44.46%,与位移传感器4相比增大了62.21%。

选取基坑开挖结束后不同工况下传感器3、传感器4、传感器7与传感器8的地表竖向位移值进行分析,结果见图5。由图可知,当基坑开挖深度为0.25 m时,随着附加荷载的增加,位移传感器3处的竖向位移分别超过报警值92%、137%、172%、424%,位移传感器4处的竖向位移分别超过报警值-48%、-17%、28%、98%,位移传感器7处的竖向位移分别超过报警值41%、77%、108%、191%,位移传感器8处的竖向位移分别超过报警值-61%、-33%、-16%、25%。

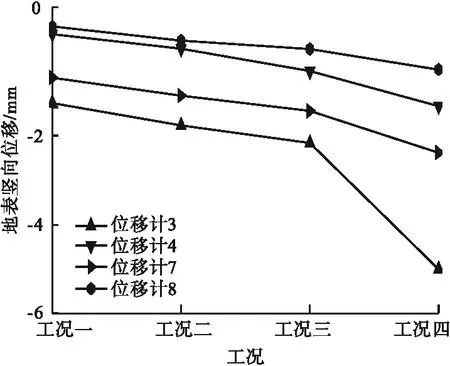
图5 不同工况下地表竖向位移值Fig.5 Vertical surface displacements under different cases

综合分析可知,基坑开挖深度增加会严重影响邻近建筑物天然地基的稳定性。当附加荷载相同时,随着基坑开挖深度的增加,建筑物基础靠近基坑一侧的地表竖向位移远大于远离基坑一侧的地表竖向位移。传感器7与传感器8的示数相差约为60%,传感器3与传感器4的示数相差约为63%,可以得出在建筑物基础中部和底边两个断面上,靠近与远离基坑位置处的地表竖向位移的差异基本相同。在建筑物平行基坑长边断面上,建筑物基础端部的地表竖向位移大于建筑物基础中部的地表竖向位移,相同附加荷载下地表竖向位移的增幅基本相同。随着附加荷载的增加,建筑物基础远离基坑一侧的角点处的地表竖向位移增幅约为35%;建筑物基础靠近基坑一侧左下角点处的地表竖向位移和建筑物基础中部地表的竖向位移增幅先减小后增大。

3 数值模拟

3.1 计算模型建立及验证

基坑开挖会影响邻近建筑物天然地基的安全性,笔者依托实际工程构建三维模型,首先分析采用隔离桩的方式对天然地基变形的影响,然后研究桩间距(1 m、2 m、3 m、4 m和5 m)和桩埋深(0 m、2 m、4 m、6 m、8 m和10 m)对天然地基变形的影响及规律。模型尺寸及网格划分如图6所示。模型所有侧面约束其法向位移,底面固定,地表面为自由面。土体材料与试验相同,采用实体单元,修正摩尔库伦本构模拟,围护结构采用板单元,弹性本构模拟,内支撑采用梁单元,弹性本构模拟。建筑物通过施加141.3 kPa均布荷载模拟。计算模型施工过程与试验相同,整个模型共有22 569个单元。待数值模型与室内试验验证后在模型中添加隔离桩,隔离桩采用梁单元模拟,弹性本构。隔离桩长为9 m,桩径为600 mm,布置在基坑围护结构与建筑物的中间位置,距基坑围护结构的水平位移为75 mm。

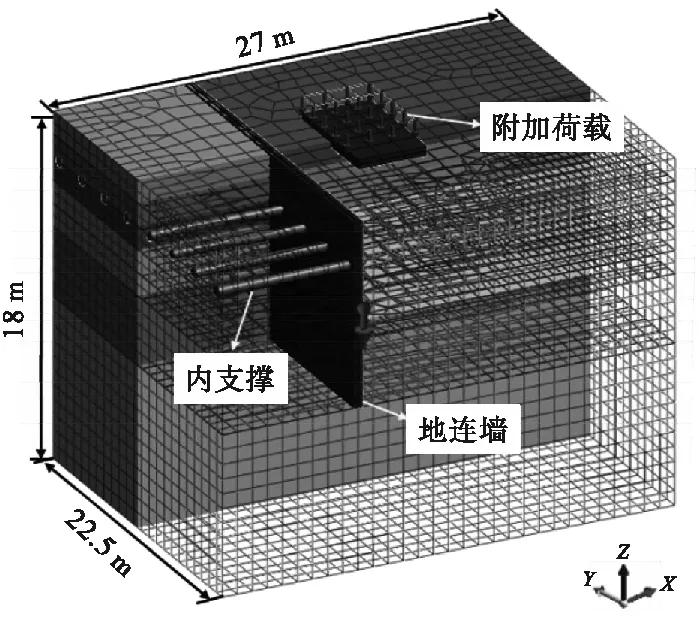
图6 计算模型Fig.6 Calculation model

在数值模型上布置监测点a和监测点b,监测点位置分别与模型试验中的传感器7和传感器8对应。将传感器7和传感器8的试验数据乘以相似比30后,与数值模型监测点的竖向位移进行对比,结果见图7。由图可知,竖向位移的数值计算结果与试验结果整体变化趋势相同,两者结果吻合度较高,最终沉降值差距均在5%以内。证明笔者建立的数值模型准确性较好,可用于后续研究。

图7 试验值与模拟值对比Fig.7 Comparison between test values and simulated values

3.2 隔离桩对天然地基变形的影响

有无隔离桩情况下基坑开挖引起的建筑物竖向位移变化规律如图8所示。

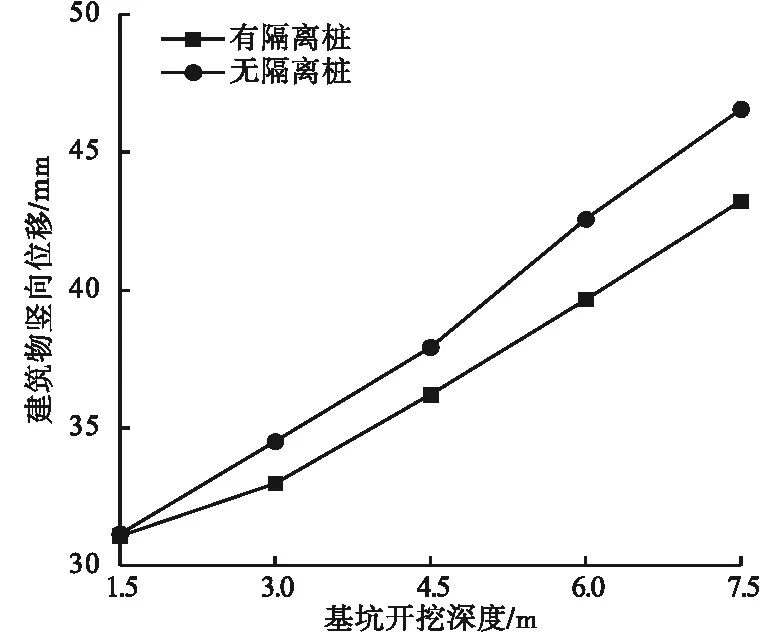
图8 不同基坑开挖深度与建筑物竖向位移关系曲线Fig.8 Vertical displacements of building under different excavation depth

由图8可知,基坑开挖深度越大,隔离桩控制天然地基变形的效果越显著。以有隔离桩工况下、基坑开挖深度为7.5 m时的建筑物竖向位移作为基准,对不同开挖深度下的建筑物竖向位移作归一化处理。随基坑开挖深度的增加,建筑物竖向位移的增幅分别为0.16%、3.51%、3.95%、6.75%、7.72%。分析可知,当基坑开挖深度小于等于4.5 m时,建筑物的位移增幅不超过5%,此时采用隔离桩的方法对天然地基变形的效果不显著,因此可选择不采用隔离桩的方法;当基坑开挖深度大于4.5 m时,采用隔离桩控制变形的方法对天然地基建筑物十分有效。因此,当基坑开挖深度较大时,可通过施作隔离桩的方式对地层变形进行有效控制,从而减小天然地基建筑物的位移。

3.3 桩间距对天然地基变形的影响

隔离桩的桩间距可以在一定程度上控制天然地基的变形,设置隔离桩间距分别为1 m、2 m、3 m、4 m、5 m,不同隔离桩间距与建筑物竖向位移之间的关系曲线如图9所示。

图9 不同隔离桩间距下建筑物竖向位移值Fig.9 Vertical displacements of building under different isolation pile spacing

由图9可知,邻近基坑建筑物竖向位移随隔离桩间距的变化呈非线性变化关系。采用隔离桩控制措施后,当隔离桩的间距增大时,建筑物竖向位移随之不断增大。相较于未采用隔离桩控制措施,邻近建筑物的竖向位移分别减小了14.99%、14.52%、13.21%、10.99%、10.41%,位移减小幅度随桩间距的增大而减小。这主要是由于隔离桩桩间土体产生的土拱效应逐渐减弱造成的。当隔离桩间距为4 m时,隔离桩间土体的土拱效应已经明显减弱;当桩间距进一步加大时,桩侧土压力进一步降低;当桩间距增大到一定值的时候,桩间土拱效应完全消失。当桩间距在1～3 m时,控制天然地基的变形效果较为显著,土拱效应的产生也比较明显;但是当桩间距过小时,虽然土拱效应很明显,由于此时隔离桩布置过于密集,基坑施工的工程量也相应增大,进而增加了施工成本,性价比不高。如何合理选择隔离桩间距,既能较好地利用土拱效应,又能充分发挥隔离桩的隔离作用,是隔离桩设计中的一个关键问题,文中工程建议桩间距取为1.5 m。

3.4 隔离桩埋深对天然地基变形的影响

为研究隔离桩埋深对控制天然地基的变形效果,设置隔离桩桩顶埋深分别为0 m、1 m、2 m、3 m、4 m和5 m,埋入式隔离桩桩长分别为常规隔离桩桩长的100%、88.89%、77.78%、66.67%、55.56%、44.44%。隔离桩埋深与邻近建筑物的竖向位移间关系曲线如图10所示。

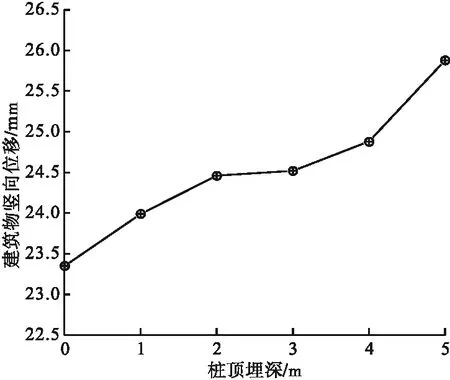
图10 不同隔离桩埋深下建筑物竖向位移值Fig.10 Vertical displacements of building under different isolation pile burial depth

由图10可知,随着隔离桩埋深的不断增大,邻近建筑物竖向位移逐渐增大,布置埋入式隔离桩与布置常规隔离桩相比,建筑物竖向位移分别增加了2.74%、4.75%、4.99%、6.55%、10.83%。分析可知,当隔离桩埋深在3 m以内(此时隔离桩桩长为常规隔离桩的66.67%)时,与常规隔离桩相比,布置埋入式隔离桩的建筑物竖向位移增幅较小,基本在5%以下;当隔离桩埋深在4 m以上时,建筑物竖向位移增幅较大。由此可见,采用常规隔离桩时,桩身在接近地表的部分对控制天然地基的变形影响不太显著,因此在基坑支护体系中加入埋入式隔离桩,可以取得和采用常规隔离桩相近的效果。在实际工程中,可以在施工要求范围内采用埋入式隔离桩,减少桩身长度,降低施工成本。