Mathematic软件在单螺杆容积计算中的应用分析研究
2023-09-13凌永骧张华宗
凌永骧,张华宗
(1.沈阳空气压缩机制造有限公司,辽宁 沈阳 440141;2.日立压缩机(苏州)有限公司,江苏 苏州 215024)
1 引言
目前工业用空气压缩机主要分为活塞式、螺杆式,其中螺杆式分为双螺杆式、单螺杆式,但是目前单螺杆式压缩机主机设计资料没有完整的设计过程及较准确的设计计算方法。
本文的重点是通过实际工作中所积累的相关资料,同时集合了相关资料总结出比较实用的设计方法及计算公式。通过Mathematic软件工具,能够快速准确地计算出单螺杆压缩机的基元容积,这样可以避免实际工程中由于基元容积的计算涉及到多重积分所涉及到繁琐的计算步骤。
另外根据相关资料中数学模型的建立,推导出单螺杆容积计算的相关公式,基于Mathematic软件,从而实现对目前单螺杆容积计算难点的解决。
2 单螺杆基本型线的成型分析和型面方程分析与介绍
在不考虑螺杆进气口缺口的影响,图1中为一完整的螺杆与星轮组合,并假定二者之间的接触线(叶片二侧接触线相当于刀刃直线)与螺杆轴线处于同一平面,在螺杆与星轮间的啮合运转中,由于星轮叶片上的接触线始终为同一条直线,而在螺杆槽的二侧面上接触线却在不断移动。因此星轮叶片的接触线上任一点在螺杆槽螺旋面上的啮合轨迹即为一条曲线。换句话说,螺杆与星轮二者间的啮合点B对于星轮来说,其位置始终固定在接触线的某一点上,而对于螺杆来说,此啮合点是不断移动的,其移动的轨迹为空间螺旋线,则进一步可确定整条啮合线(即接触线)在螺杆上移动的轨迹为一空间螺旋面。

图1
此接触线一方面在垂直于星轮轴的平面内绕着星轮轴线转动,另一方面又绕着螺杆轴线转动。这二个转速之比等于二者的齿数之比Zr/ZR。根据这个分析和其他既定的几何参数,就可确定任一啮合点B在螺杆上的移动轨迹(螺旋线)方程。进一步推论下去(使B沿接触线移动),即可得到整个接触线上的移动轨迹(螺旋面方程)。螺旋槽二侧螺旋面形状完全相同,仅仅相差一个随半径变化的相位角。于是,根据同一个型面代入不同的起始条件,即可求出二侧型面的参数坐标。
由于螺杆为圆柱形,其螺旋面是母线,按一定规律绕自身轴线旋转形成的,故采用圆柱坐标(不用直角坐标)。根据母线又在星轮叶片二侧星轮轴线转动这一特点,采用星轮转角θ和母线上各点与星轮中心的距离——转动半径r为参变数,求解型线方程最为简单。
图1上个符号参数解释如下:
Br——星轮叶片右侧接触线(母线)上任意点
BR——螺杆螺旋槽侧面上与Br相啮合的螺旋线上的任意一点
B——当OrBr转至θ角时,Br刚好与BR相互啮合的位置
Or——星轮旋转中心
OR1OR2——螺杆旋转轴线
OrQ——通过Or点与OR1OR2平行的直线(OrQ与OR1OR2组成的平面与星轮轴线垂直,Br始终在这个平面内移动)
θ——Br绕Or点转动的角度(以OrQ为θ角的起始位置)
A——Or与OR1OR2的垂直距离(即螺杆与星轮间的中心距离)
hr——Or与螺杆外圆柱面的垂直距离

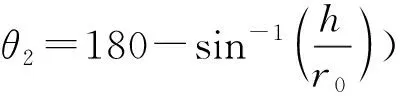
r——Br至Or的回转半径
r0——星轮叶片外圆半径
R——BR绕OR1OR2的回转半径
R0——螺杆外圆半径
φ——螺杆与星轮相互啮合时 ,Br由θ1转至θ刚好与BR绕啮合,在这同一段时间内,BR绕OR1OR2转过的角度(φ角度在OR1OR2的垂直平面内,图上画法为非正规投影 )
L——BR绕OR1OR2的旋转平面与通过右端点F且垂直于OR1OR2的平面间的距离
Zr——星轮叶片数
ZR——螺杆头数
b0——叶片宽度(即叶片二侧相互平行的接触线间的距离)
α——螺杆螺旋面上任一点BR之螺旋角(螺旋角的定义为通过BR的螺旋面之切线与叶片旋转平面间的夹角。当螺杆上的BR绕点与星轮叶片上的Br点在B点啮合时,该切线必须与OrB垂直)
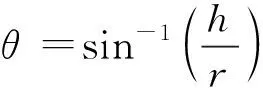
α0——θ=90°时的α0
求解由啮合点B走出的以BR点的圆柱坐标来表示的螺旋面方程:
以星轮叶片上的点Br的极坐标(r,θ)为参量变数,由图1的几何关系和前述运动分析得啮合点B在螺杆上移动的轨迹,空间螺旋面上任一点BR的圆柱坐标参数方程:
(1)L=r0cos(θ1)-rcos(θ)
(2)R=A-rsin(θ)
(3)φ=(Zr/ZR.)·(θ-θ1)
再求解Br点斜率tanα及螺旋角α:
设UBR、UBr分别为BRBr在B点啮合时刻各自绕螺杆轴和星轮轴旋转的圆周线速度。
则得:tanα=(UBR/UBr)=(R/r)·(ωR/ωr)
式中ωR——螺杆转动角速度
ωr——星轮转动角速度
ωR/ωr=Zr/ZR;
得
tanα=(Zr/ZR)·(R/r)=(Zr/ZR)·((A-rsin(θ))/r)
根据求出不同(r,θ)处的螺旋角α、β,可初步设计出能在螺旋槽内来回自由滑动的星轮叶片截面形状。如图2所示,二侧BB′点表示二条接触线(二条母线通过这二点而相互平行)。BB′连线在OrQ与OR1OR2构成的基准平面内。为避免叶片与螺旋槽的相互干涉,则在BB′上下两段厚度内,叶片侧面与通过BB′的基准平面的夹角应以α0、β为界
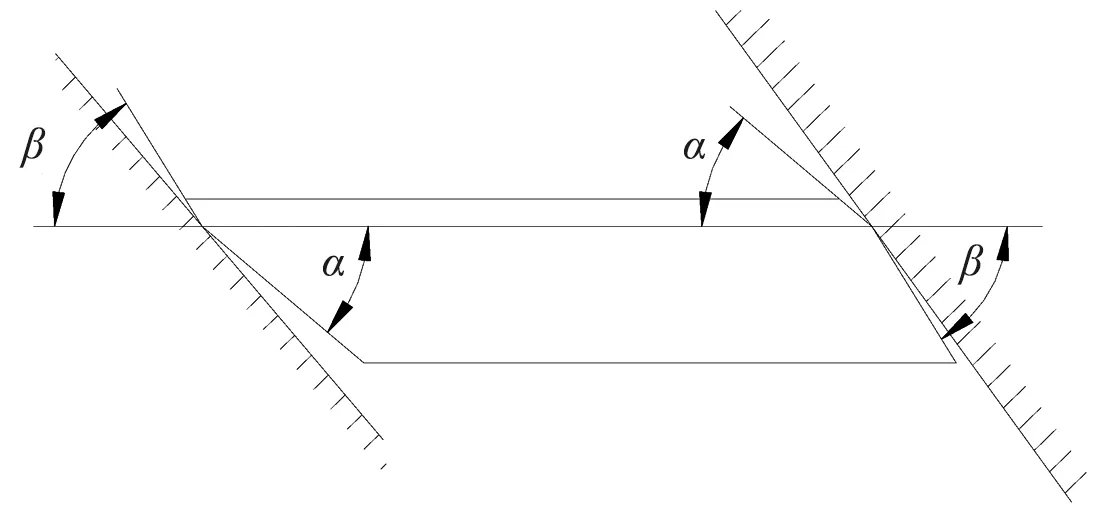
图2
(即≤α0和≥β)。由此得出与基本型线螺杆相配合的叶片截面形状。
3 单螺杆基元容积计算数学公式实际应用
本文的重点是分析介绍Mathematics基元容积计算过程中实际应用问题。为了计算方便起见,不在过多的介绍具体计算公式推导过程。如需了解具体推导过程可以参考相关介绍的参考文献资料。
根据引用的相关将单螺杆容积计算参考资料,可将需要计算的基元容积资料分为二部分:
(1)第一部分容积计算公式
第一部分为叶片从刚开始封闭螺杆θ1时,扫描的容积过程中叶片所旋转的角度到θ21,
(2)第二部分容积计算公式
第二部分为叶片从前侧边开始脱离螺槽的旋转角度θ21时,直至后侧边完全脱离螺槽后旋转角度θ3时,即为整个叶片转过的角度。

具体容积公式推导为了简单起见,现对其过程不再分析讲解。只针对现有容积计算公式的实际应用集合具体的算例进行分析,以方便更多人员在实际中解决单螺杆容积计算繁琐的问题。
同时现以相关实际数据进行实际计算容积并验证对比其正确性。
星轮半径:r0=115;螺杆半径R0=115;星轮叶片数Zr=6;螺杆头数ZR=11;h=70;叶片宽度;b0=34;θf=60°;
=60.645°=1.059弧度
=134°=2.338弧度
则根据以上第一部分容积计算公式:
=292.718 cm3
第二部分容积计算公式:
θ21=134°=2.338弧度
=151°=2.635弧度
(Acosθi-r0sinθicosθi)dθidθ)
(185cosθi-115sinθicosθi)dθidθ)
=14.02 cm3
最后单个螺旋槽的总容积
V=V1+V2=292.718+14.02=306.7383 cm3
整个螺杆6个螺旋槽容积之和为
V0=6V=306.738=1840.428 cm3
目前需将相关公式即数据代入Mathematics软件,并且按照软件使用方法计算容积数据,并且根据计算所得结果与实际计算数据进行对比,进而也进一步验证采用此软件计算与人工计算相比的准确性,也进一步较少人工计算的复杂性,从而提高实际设计效率。
