融合多维超声时频域特征的锂离子电池荷电状态估计

刘素贞 陈云龙 张 闯 金 亮 杨庆新

融合多维超声时频域特征的锂离子电池荷电状态估计

刘素贞1,2陈云龙1,2张 闯1,2金 亮1,2杨庆新1

（1. 省部共建电工装备可靠性与智能化国家重点实验室（河北工业大学） 天津 300130 2. 河北省电磁场与电器可靠性重点实验室（河北工业大学） 天津 300130）

准确地估计锂离子电池的荷电状态（SOC）对电动汽车的安全运行至关重要。传统方法通过电池电压、电流、温度等参数估计SOC，但参数依赖对电极行为的测量，且易受阻抗、充放电速率等因素影响。相对于传统信号，超声信号可区分电池材料物理性质的微小变化，从而准确地表征电池状态。该文首先通过连续均匀分层介质模型研究了超声波在电池内部的传播过程，进而分析了电池材料物理性质对超声波传播特性的影响；其次，搭建了锂离子电池超声检测平台，提取了多维超声时频域特征，并利用超声特征解释了电池内部的电化学过程；最后，通过长短时记忆神经网络建立了融合多维超声时频域特征的锂离子电池SOC估计模型，对比了融合不同特征对SOC估计精度的影响。实验结果表明，融合多维超声时频域特征可以有效提高SOC估计的精度。在动态工况下，SOC估计的方均根误差在1.46%以内，平均绝对误差在1.15%以内，验证了方法的有效性和准确性。

锂离子电池 荷电状态 超声检测 长短时记忆神经网络 多维超声特征

0 引言

锂离子电池荷电状态（State of Charge, SOC）是电池管理系统（Battery Management System, BMS）的关键参数[1]，当电池SOC估计不准确时，会导致其过充过放[2]，加剧容量衰减，甚至引发一系列安全问题[3-4]。因此，准确地估计电池的SOC可以使电池工作在最佳状态[5]，确保电动汽车安全可靠运行[6-7]。然而，SOC无法直接测量，且易受环境温度、老化程度等因素影响，只能通过电压、电流、内阻等与电池工作状态相关的参数进行估计。同时由于电池的高度非线性及时变特性，使得电池SOC的精确估计成为了难点[8]。

目前，常用的SOC估计方法主要有基于表征参数的方法、安时积分法、基于模型的方法及数据驱动法[9]。基于表征参数的方法分为内阻法和开路电压法等，方法简单易实现，但难以适用于实际工况[10]。安时积分法可在线估计SOC，但其误差会逐渐积累[11]。基于模型的方法估计精度高、实时性好，但精度依赖模型的准确度[12]。数据驱动法对解决强非线性问题有显著优势，估计精度高，但需要大量数据作为先验知识，若数据不能充分反映电池特性，就会造成模型过拟合[13]。上述方法所用的电压、电流、温度等参数依赖对电池两电极行为的测量，易受阻抗、充放电速率的影响，且无法体现充放电过程中电池内部的电化学过程。实际上，电池在充放电循环过程中，锂离子在正负极之间嵌入和脱出会引起电池内部结构的变化，从而改变其内部材料的物理性质，其中最显著的是正负极材料杨氏模量和密度的变化[14]。因此，锂离子电池内部状态变化与电池动力学行为和材料结构密切相关，如何获取多重耦合因素影响下电池内部的动力学行为和材料结构随电池内部状态的变化规律是电池研究领域的一个难点。

近年来，超声检测因灵敏度高、通用性强等优点，在电池状态检测领域得到广泛应用。相比其他原位表征手段，超声检测无需对电池进行任何加工、涂覆及拆解，在不损坏其内部材料的前提下，利用电池内部材料物理性质变化导致的声学性能差异来检测电池内部材料的微小变化，能够实时、原位、无损地表征电池内部状态[15]。目前，超声在电池状态检测领域的研究主要是基于信号飞行时间（Time of Flight, TOF）和信号幅值（Singal Amplitude, SA）两个信号时域特征来表征电池SOC[16]。A. G. Hsieh等通过电池正负极材料密度和杨氏模量的变化规律，将声速变化与电池SOC联系起来，发现TOF与SOC之间存在线性关系[17]。Chang Junjie等利用Biot流体饱和多孔介质模型分析超声波在电池中的传播特性，建立了SA与电池SOC之间的近似线性关系[18]。P. Ladpli等发现TOF和SA与电池充放电循环和老化之间的强相关性，并建立分析声学模型来模拟循环过程中电极杨氏模量和密度的变化，进而验证了这种相关性[19]。G. Davies等采用TOF、SA及电池电压等数据，基于支持向量机建立了电池SOC估计模型，误差约为1%[20]。P. Ladpli等提出基于Gabor字典的匹配追踪算法，将原始超声波形分解为数个“原子波”，提取原子波参数并结合电池电压作为预测特征，提高了SOC估计的精度[21]。实际上，电池内部结构复杂、电化学过程较多，且动力学过程涉及到复杂的多场耦合问题，目前超声对电池状态估计的研究仅利用TOF、SA等时域特征，缺乏对多参数的综合分析。时域特征存在局部非线性，且TOF对硬件采样要求较高，会降低电池SOC估计的精度。同时，由于超声信号是非线性、非平稳信号，仅利用时域特征无法体现出超声信号在不同尺度下的变化。

针对上述问题，本文在现有研究基础上，通过在室温（25℃）条件下对软包钴酸锂（LiCoO2, LCO）电池进行循环充放电和超声检测实验，得到电池充放电过程中的超声信号。首先，对超声信号进行时域分析，提取TOF、SA等时域特征；其次，利用快速傅里叶变换（Fast Fourier Transform, FFT）对信号进行频域分析，提取信号频谱峰值等频域特征，并利用时、频域特征解释电池内部的电化学过程；然后，结合集合经验模态分解（Ensemble Empirical Mode Decomposition, EEMD）分析非线性、非平稳信号的优势，对信号进行时频域分析，提取其本征模函数（Intrinsic Mode Function, IMF）的斜度、峰度、峰值指标、裕度指标、形状指标、脉冲指标等无量纲特征，以得到超声信号在不同尺度下的特征信息；最后，考虑到长短时记忆（Long-Short-Term Memory, LSTM）神经网络对时序信号的特殊处理能力，在进行特征选择后，结合电池的电压、电流、温度等特征，提出一种融合多维超声时频域特征的锂离子电池SOC估计方法，实现SOC的精确估计。

1 超声检测锂离子电池SOC原理

1.1 超声波在电池内部的传播过程

锂离子电池可视为多层复合材料，由于电池不同层间材料的成分和结构不同，造成其层间的声学特征参量亦各有差异，可用连续均匀分层介质模型来模拟超声波在电池中的传播过程[22]。锂离子电池连续均匀分层介质模型如图1所示，图中Z、E、c、ρ、α、x分别为电池内部第层材料的声阻抗、杨氏模量、声速、密度、衰减系数、厚度，ri、ei分别为第个介质分界面处的声波透射系数与声波反射系数。

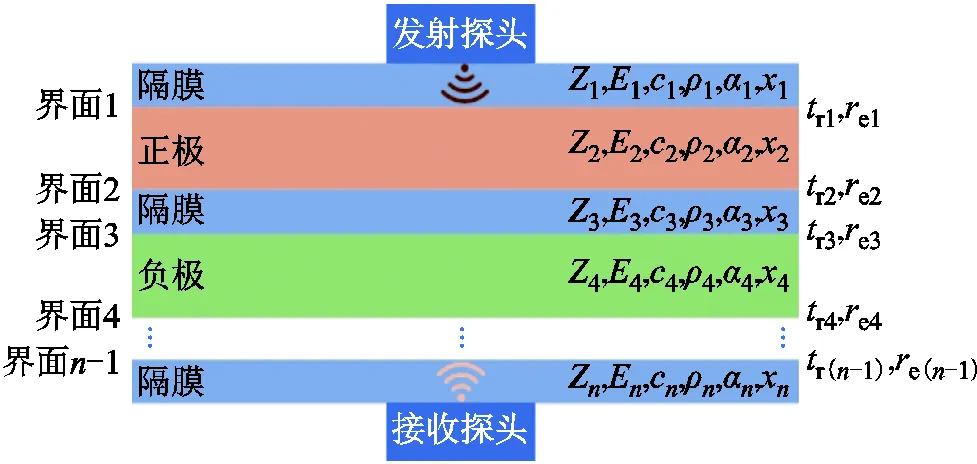
图1 锂离子电池连续均匀分层介质模型

当超声波通过多层介质传播时，声波被不同程度地散射、反射和吸收，不同材料介质界面对声波的反射及透射情况都与材料声阻抗紧密相关。声阻抗是表示介质对声波阻碍作用强弱的物理量，是介质的一种声学特性表征，其表达式为

由式（1）可以看出，材料密度和杨氏模量共同影响着声阻抗。材料声阻抗越大，表明对声波的阻碍作用越大，声波穿过材料时能量衰减越多，声波幅值越小。由介质的声阻抗计算得到声波穿过各界面时的透射系数ri与反射系数ei分别为

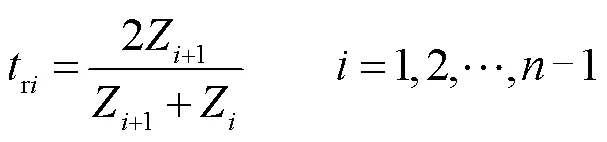
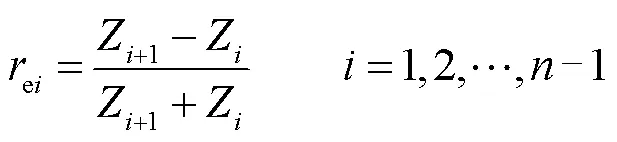
在连续均匀分层介质模型中，当超声波垂直入射时，忽略声波的散射作用，只考虑纵波传播，则它对超声波的作用可以用界面的反射、透射作用及超声衰减作用的总和来表示。

超声波由电池上表面入射后，遇到每一个界面均会发生反射与透射，会连续受到1个界面的反射与透射作用，表示为

对于层状介质，当忽略超声波在传播过程中的非线性效应时，可认为超声波在传播过程中波形不发生变化，而仅是振幅的衰减。则当超声波由电池上表面传播到电池下表面后，会受到层介质的衰减作用，表示为

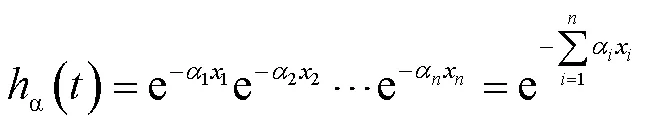
则探头接收到的纵波响应为

式中，()为输出；()为输入；()为高斯白噪声；“*”为卷积运算符。

在实际情况下，由于电极材料表面不平整，材料孔隙率不同及化学反应随时发生等原因，会导致超声波在实际情况下的传播过程更为复杂。

1.2 超声波传播特性与电池SOC之间的关系

电池SOC表示锂离子在电极颗粒中的浓度分布，即电池正负极材料锂化程度。电池充放电过程中，锂离子在正负极之间嵌入嵌出，在影响电池材料物理性质的同时，也会导致电池SOC改变。

超声纵波在每层电极材料中的传播速度由材料的多种物理性质决定，可用超声波在各向同性均匀介质中的声速公式来表示，即

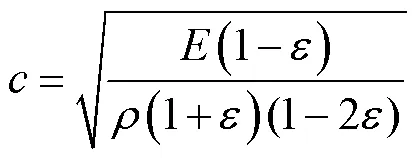
式中，为材料的泊松比。对于各向同性材料而言，杨氏模量和泊松比是两个基本材料常数，可确定材料的弹性性质。则声波飞行时间为

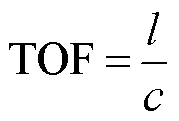
式中，为超声波传播路径长度，即电池厚度。由式（7）、式（8）可以看出，材料弹性性能越强、密度越小，则声波传播速度越大，飞行时间就越短。

综上所述，电池内部各层电极材料的密度和杨氏模量影响材料的声阻抗，声阻抗越大，声波能量衰减越多，其幅值（SA）越小；电极材料的密度、杨氏模量及泊松比影响声速，声速越高，声波飞行时间TOF越短。因此，超声波在电池内部的传播特性与电池内部材料的物理性质密切相关，可以通过超声特征将电池SOC与内部材料物理性质联系起来，超声波具有表征电池SOC 的潜力。

2 超声测试系统及实验方案

2.1 超声测试系统的搭建

实验采用两块具有相同老化状态的商用SP376080SI软包LCO电池，编号为A1、A2。实验过程中两块电池均采用完全相同的实验步骤及设置。电池额定容量为3 435 mA·h，上、下截止电压分别为4.45 V、3 V。锂离子电池超声检测平台如图2所示，使用NEWARE CT-4008电池测试系统对电池进行充放电循环的同时连接上位机进行电压、电流、温度等数据的采集。将热电偶放置在电池表面正中心以实时监测其充放电过程中的温度变化。使用CTS-8077PR型超声波脉冲发生接收仪配合 5 MHz压电超声探头对电池底部两侧相对位置进行压电加载，以发射和接收透过电池的超声纵波。利用Tektronix MSO44混合信号示波器实时显示超声信号，同时结合上位机每30 s采集一次超声信号。实验过程中为保证波的传输效率，在探头与电池表面间涂上甘油耦合剂以维持长时间的在线测量，同时使用电池夹具和压力传感器固定探头的位置并向探头施加大小相同的预紧力。考虑到环境温度和电池本身温度对超声信号的影响，将夹具及压力传感器置于电池底部并与电池一同置于GD-JS4005高低温湿热试验箱中，保持试验箱温度恒定为25℃。

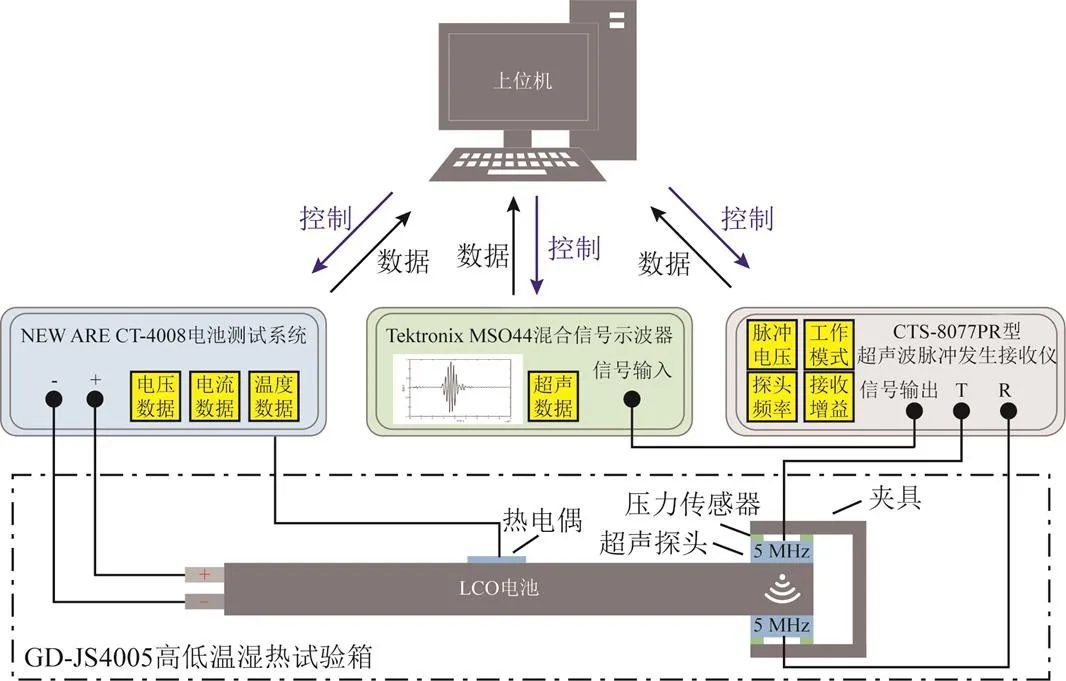
图2 锂离子电池超声检测平台示意图

2.2 实验方案与数据预处理

先采用恒流恒压充电策略对电池充电，充满电搁置10 min后进行恒流放电，具体设置见表1。

表1 锂离子电池充放电策略

Tab.1 Charge and discharge strategy of lithium-ion battery

考虑到Savitzky-Golay（S-G）滤波器是一种基于局域多项式最小二乘法拟合的滤波方法，其特点是在滤除噪声的同时可以保持信号的形状、宽度不变。因此，采用S-G滤波器对采集到的超声信号进行降噪处理，以减小环境、实验设备等因素对超声信号的干扰。与原始信号对比，降噪后超声信号的信噪比可达152 dB，方均根误差为9.93×10-4，采用S-G滤波器可以有效地降低高频噪声信号，并对原始超声信号进行平滑处理。

3 多维超声时频域特征提取与电池SOC估计

3.1 多维超声时频域特征提取

在对原始超声信号进行预处理后，从多维度对信号进行分析以提取与电池SOC呈高相关性的多维超声时频域特征，作为电池SOC估计模型的输入，进而实现电池SOC的准确估计。本节将从超声时域特征提取、频域特征提取及时频域变换特征提取三个方面进行阐述。

3.1.1 超声时域特征提取

图3与图4为一个充放电周期内超声信号随电池SOC的变化，可以看出，在电池充放电过程中，超声信号随着电池充放电呈周期性变化。波形变化的主要原因是在电池充放电循环过程中，锂离子在正负极之间转移，电池内部材料的电化学性能及力学性能改变，同时材料的晶格结构相应变得增强或松弛，进而影响了材料的阻尼和衰减特性，导致超声波在电池内部传播时的速度与衰减程度不同。另外，由于材料性能在循环过程中不断变化，使得即使在电化学信号（如电压、电流、温度等）仅有极小的变化时，也能够利用超声信号区分材料性能的明显变化，进而准确地判断电池状态。

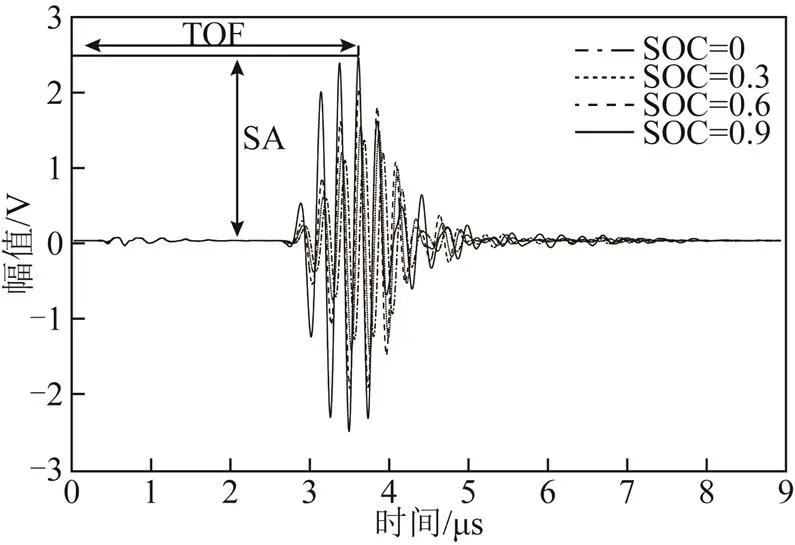
图3 电池充电过程超声信号变化

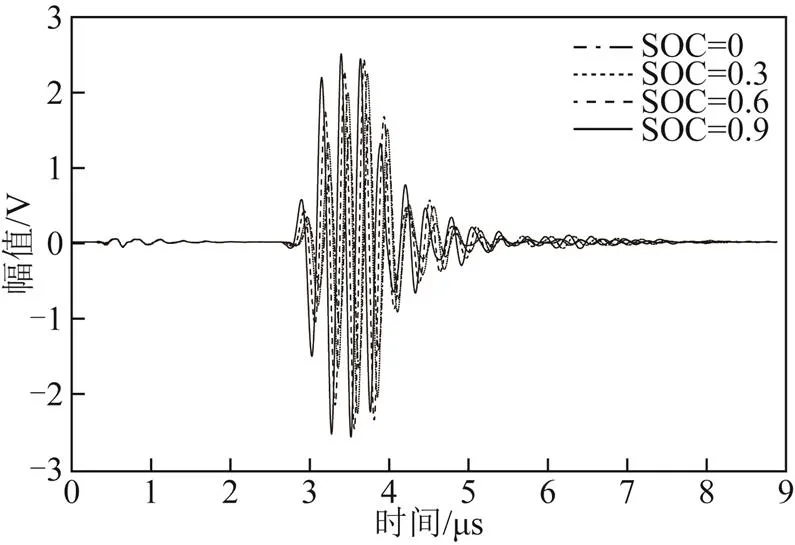
图4 电池放电过程超声信号变化

由图3所示的超声时域信号提取超声信号的TOF与SA，结果如图5所示。可以看出，在充电初期（0～0.05 SOC），由于对电池突然施加激励，电池内部出现浓差极化现象，其材料物理性质变化较剧烈，TOF与SA快速衰减。在充电中期（0.05～0.73 SOC），随着恒流充电过程的进行，锂离子迁移速度逐渐达到平衡，电化学反应过程趋于稳定，因此TOF与SA变化较为均匀。对于TOF，一方面，电池充电时厚度增加[20]使得超声波传播路径增加，导致其TOF增大；另一方面，在电池充电过程中，电池内部正负极材料的杨氏模量与密度之比增加，导致超声波波速增大，TOF减小。因此，由图5可以看出，在此阶段，电池正负极材料物理性质的变化是导致TOF变化的主要因素。对于SA，通常情况下，材料越坚硬、紧凑，其阻尼越小，信号的固有衰减也越小。因此，当电池充电时，其正负极材料的杨氏模量增加，材料刚度增大，声阻抗减小，超声信号衰减程度变小，SA增加。在充电后期（0.73～0.93 SOC），由恒流充电改为恒压充电，充电电流逐渐减小至截止电流。因此，在恒压充电过程中，电池内部电化学反应速率逐渐减小，锂离子迁移速度减小，正负极材料物理性质变化程度减小，因此SA变化逐渐平缓，且变化趋势与恒流充电时相同。但是TOF却表现出了与恒流充电过程相反的趋势，这是因为在充电后期，由于电化学反应速率减小，电池厚度变化对TOF的影响相对于内部材料物理性质变化对TOF的影响逐渐占据主导地位，因此TOF有所增大。

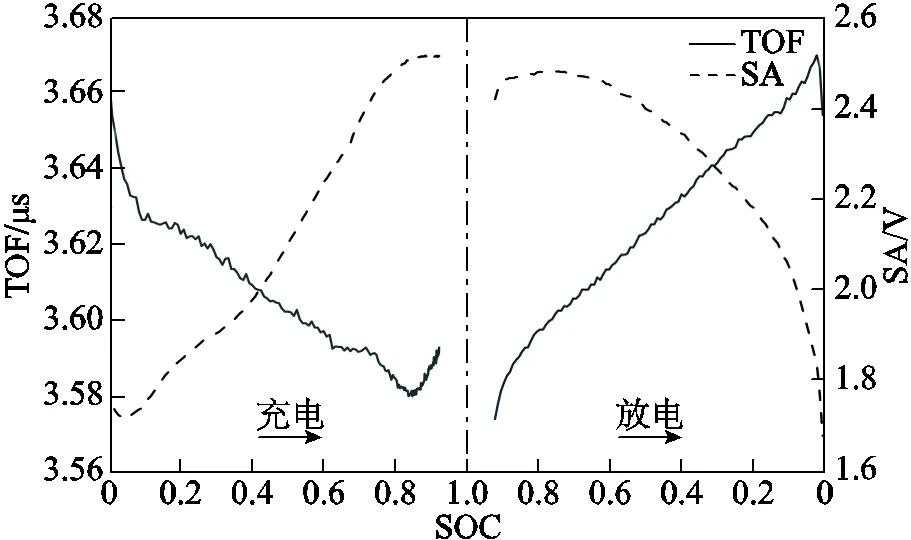
图5 电池充放电过程中超声信号时域特征变化

在电池放电过程中，其内部电化学过程、正负极材料物理性质及电池厚度变化均与充电过程相反，因此，TOF与SA的变化也与充电过程相反。

3.1.2 超声频域特征提取

考虑到频域分析通常能够提供比时域分析更加直观的特征信息，因此利用FFT对超声信号进行频域分析，提取频谱峰值m作为超声信号频域特征，如图6所示。实际上，声波在电池内传播时会受到多个界面的作用而来回反射和透射，进而削弱声波的能量并产生多种频率的谐波信号，最终叠加在一起被超声探头接收。而m代表着在声波传播过程中某种频率信号所携带的相对其他频率信号较大的能量，是声波在电池中未经反射而直接沿电池厚度方向透射出来的某种频率信号所对应的能量。从图6中可以看出，其随电池SOC的变化规律大致与SA相同，但是由于排除了其他频率谐波信号的影响，其与电池SOC的相关程度更高。此外，m所对应的频率并不是恒定不变的，而是随着电池充放电过程在一定范围内循环变化。原因是在电池充放电过程中，锂离子在正负极之间来回嵌入脱出使电极材料性质、界面形态及多个界面间距离等因素发生变化，会导致声波在层间来回反射时产生不同频率的谐波信号。这种现象说明了利用超声信号变化反映电池内部电化学过程的潜力，同时也证明了使用超声信号表征电池SOC的可行性。

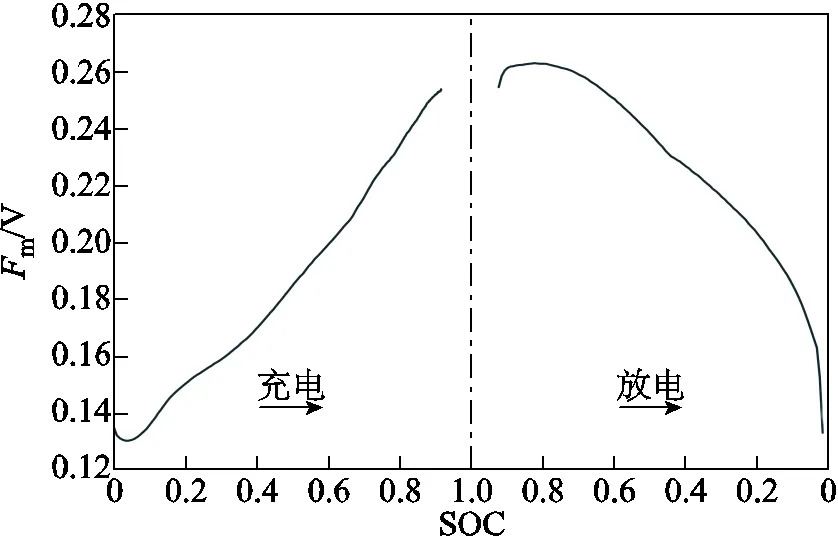
图6 电池充放电过程中超声信号频域特征变化

3.1.3 超声时频域变换特征提取

实际工况下，噪声、耦合剂等非线性因素会对超声信号产生不同程度的影响，且时、频域分析各有其优缺点，单靠时域或频域分析难以充分挖掘出信号的丰富信息，时频域分析则弥补了这一点，其在分析非线性、非平稳信号方面具有很大的优势。集合经验模态分解（EEMD）依据信号本身尺度特征对信号进行分解，并利用高斯白噪声改变了信号极值点特性，可以较好地抑制经验模态分解在分解过程中出现的虚假变量和模态混叠等问题，得到信号在不同尺度下的特征信息[23]。电池超声信号经过EEMD分解后，共得到14个本征模态函数（Intrinsic Mode Function, IMF）分量及1个信号残差，其中IMF1～IMF5为低幅值高频率噪声信号，IMF6～IMF14分量如图7所示。

图7 超声信号经EEMD分解得到的各IMF分量

为降低特征维数及计算复杂度，同时保证基本涵盖原始超声信号的所有信息，利用各IMF分量的方差贡献率及其与原始超声信号的相关系数选择合适的IMF分量进行分析。方差贡献率是指每个IMF分量的方差占所有IMF分量方差和的比，方差贡献率越大代表此IMF包含的信息越丰富。相关系数是反映变量间相关程度的统计指标，其绝对值越接近1，表明两个变量越相关。二者计算过程分别为：

设IMF（=1, 2,…,）对应的方差为D（=1, 2,…,），则对应的方差贡献率为

各IMF分量与原始信号的相关系数为

式中，Cov(IMF,)为IMF和原始信号之间的协方差；D为原始信号的方差。

根据式（9）、式（10）得到各IMF分量的方差贡献率与相关系数如图8、图9所示。可以看出，IMF6、IMF7和IMF8的方差贡献率与相关系数较大，所以超声信号包含的信息主要体现在IMF6、IMF7和IMF8分量中。

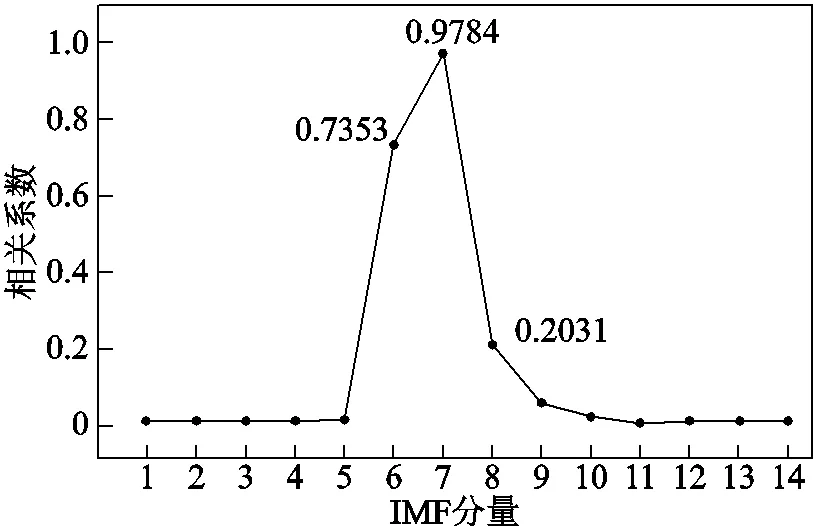
图9 各IMF分量与原始超声信号的相关系数

基于以上分析，选择IMF6、IMF7、IMF8作为信号特征提取的对象，并对每个IMF分量进行无量纲参数的提取。无量纲参数的提取过程如下。

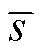
1）斜度

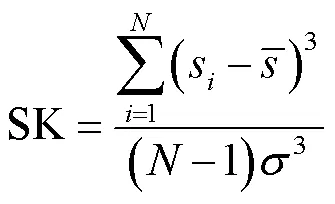
2）峰度

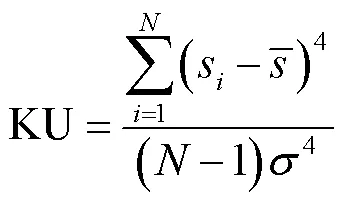
3）峰值指标

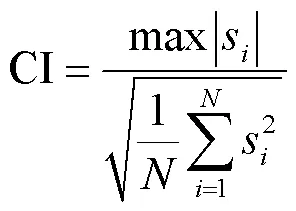
4）裕度指标

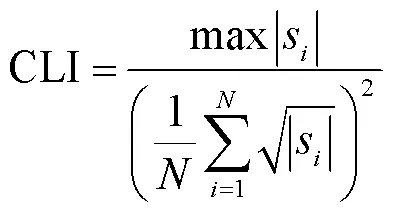
5）形状指标

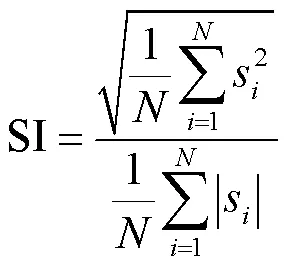
6）脉冲指标

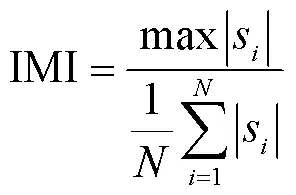
在对IMF6、IMF7和IMF8分量分别提取6个无量纲特征后，求各特征与电池SOC的Pearson相关系数，见表2。

表2 超声时频域变换特征与电池SOC的Pearson相关系数

Tab.2 Pearson correlation coefficient between ultrasonic time-frequency domain transform features and battery SOC

选取CLI6（IMF6的CLI特征，下同）、CLI7、CLI8、KU7和KU8五个与电池SOC相关性较高的时频域变换特征，并结合超声时域、频域特征及电池电压、电流、温度等传统特征作为估计模型的输入，进一步提高电池SOC估计模型的精度。

3.2 基于LSTM的锂离子电池SOC估计

3.2.1 LSTM算法基本原理

循环神经网络（Recurrent Neural Network, RNN）在处理时间序列数据方面有独特优势，但是在训练过程中会出现梯度消失和梯度爆炸的问题。LSTM网络继承了RNN的部分特性，且具有专门的记忆单元，克服了RNN梯度消失和梯度爆炸的问题，能够挖掘时间序列数据内部规律[24]。LSTM结构示意图如图10所示。

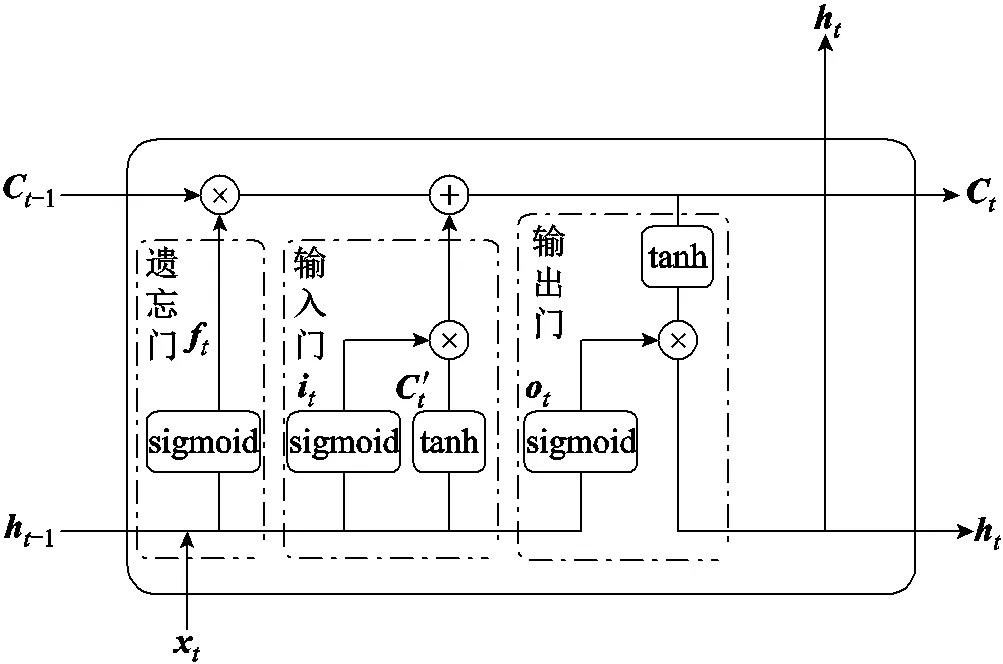
图10 LSTM结构示意图

每个LSTM细胞通过遗忘门、输入门、输出门三个门结构的信息输入和输出控制其状态。遗忘门负责保留部分前一时刻细胞状态信息，输入门负责调节保留进入细胞的新信息，输出门负责控制当前时刻细胞输出。其前向通路计算公式为

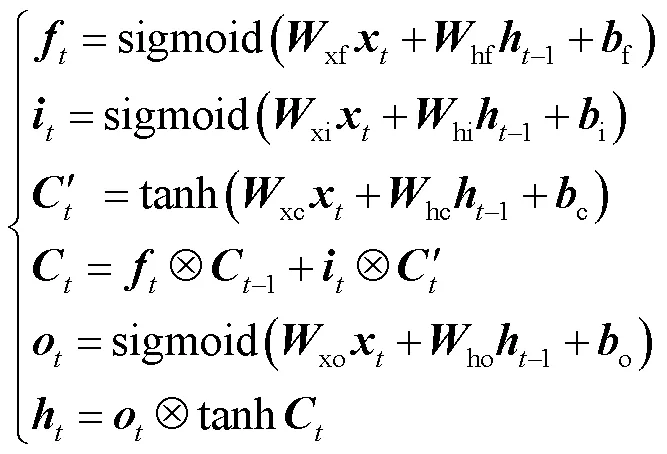
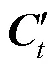
LSTM神经网络的训练过程就是在设定好网络结构的基础上，通过对网络各细胞的权重矩阵和偏置矩阵随机初始化，将模型的输出与理想值之间的误差反向传递，求解细胞各权重矩阵和偏置矩阵的梯度下降方向并实时更新参数，直至训练逐渐收敛且误差达到要求的过程。

3.2.2 基于LSTM的锂离子电池SOC估计

本文采用LSTM神经网络，将电池A1在一个循环内的电压、电流、温度等3个常规特征，以及2个超声信号时域特征、1个超声信号频域特征、5个超声信号时频域变换特征共计11维特征归一化处理后作为训练集，将与电池A1具有相同老化状态的电池A2的数据归一化处理后作为测试集，用于SOC估计效果的测试，具体流程如图11所示。在LSTM模型的结构方面，模型有11个输入节点、1个输出节点、2个隐含层，每个隐含层包括10个隐含节点。模型训练集大小与电池充放电过程持续时间及超声信号采集间隔有关。在充电过程中，训练集大小为12×202；在放电过程中，训练集大小为12×108。测试集大小与训练集大小对应相同。模型学习率设置为0.02，采用平均绝对误差（Mean Absolute Error, MAE）作为损失函数，并使用Adam优化器提高模型运算速度和效率。此外，为了合理地评价模型的预测精度，引入方均根误差（Root Mean Square Error, RMSE）、平均绝对误差及决定系数23个评价指标对模型进行评价，其公式分别为

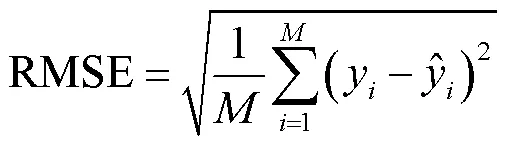
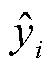
基于LSTM的锂离子电池SOC估计结果与基于深度神经网络（Deep Neural Networks, DNN）、卷积神经网络（Convolutional Neural Networks, CNN）的SOC估计结果对比如图12所示。其中，图12a为电池充电过程SOC估计结果对比，图12b为电池放电过程SOC估计结果对比。各评价指标见表3。可以看出，相对于基于DNN和基于CNN的SOC估计，由于LSTM对时序数据的处理能力，其SOC估计精度更高。同时相对于文献[25]中利用超声时域特征SA，并结合反向传播（Back Propagation, BP）神经网络实现电池SOC估计的方法，本文估计精度更高。在电池充电过程中，SOC估计值与真实值高度吻合，方均根误差在0.85%以内，平均绝对误差在0.58%以内。在电池充电初期误差相对较大，但是随着充电过程的进行，误差逐渐减小，这也反映了LSTM能够通过时间序列很好地捕捉SOC的变化及其对电池历史状态的依赖性。在电池放电过程中，SOC估计的方均根误差在0.37%以内，平均绝对误差在0.24%以内。随着放电过程的进行，估计误差逐渐减小。同时，在充放电过程中，所建立的LSTM模型的决定系数R2均在0.995 3以上，也表明了结合LSTM模型对电池SOC进行估计时，模型的拟合效果较好，其对估计值的解释能力较强，SOC估计精度较高。

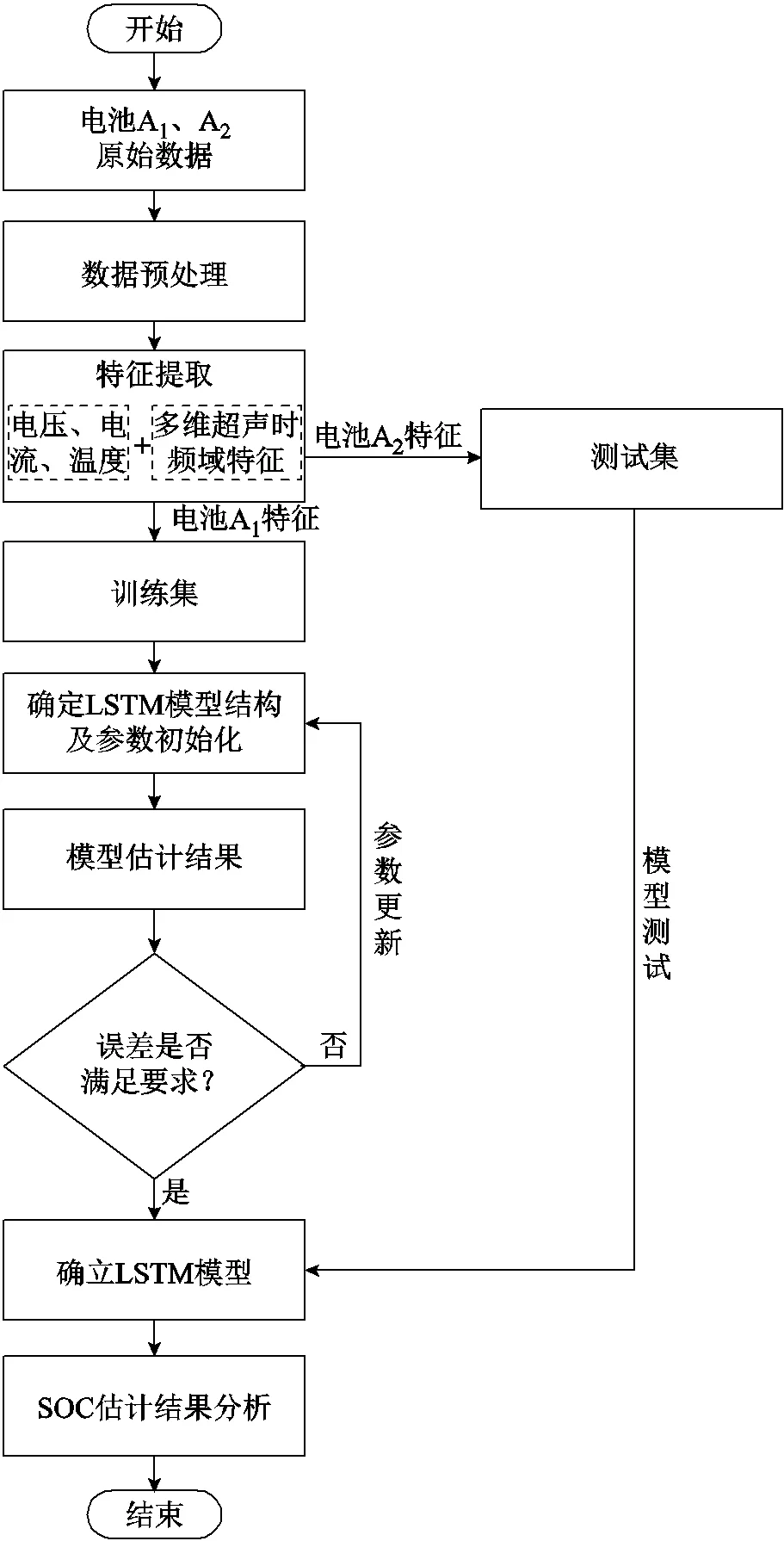
图11 融合多维超声时频域特征的锂离子电池SOC估计流程

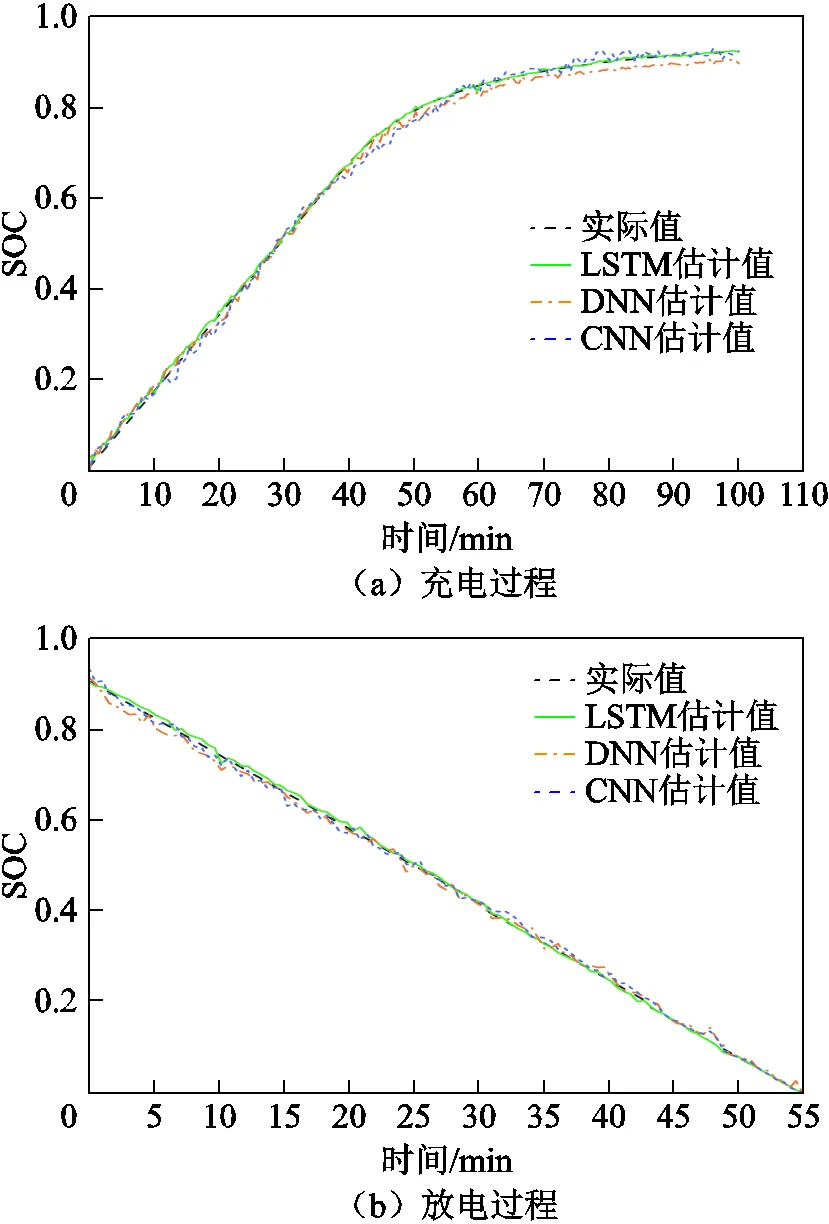
图12 融合多维超声时频域特征的锂离子电池SOC估计结果对比

表3 融合多维超声时频域特征的锂离子电池SOC估计精度对比

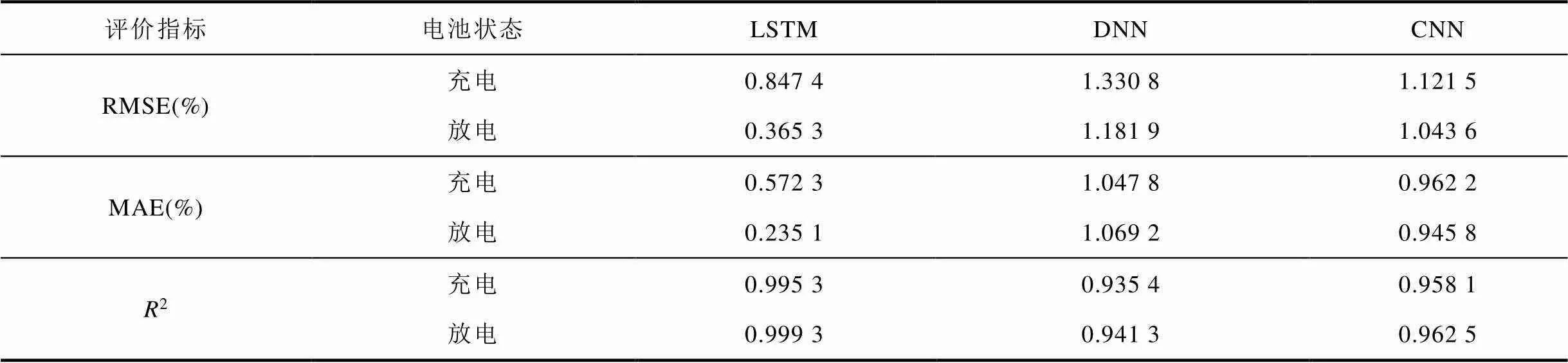
Tab.3 Comparison of SOC estimation accuracy of lithium-ion battery fused with multi-dimensional ultrasonic time-frequency domain features

为了进一步量化融合多维超声时频域特征对电池SOC估计的优势，对比了使用不同的特征作为LSTM模型的输入时，电池SOC的估计精度差异。对比包括以下两种情况：①仅使用电池电压、电流、温度共3个特征；②使用电池电压、电流、温度及2个超声信号时域特征共5个特征。两种情况的SOC估计精度见表4、表5。对比表3～表5可知，仅使用电池电压、电流、温度3个特征作为LSTM模型的输入时，电池SOC估计的方均根误差大于1%，平均绝对误差也在1%左右；当在此基础上融入2个超声信号时域特征作为输入时，SOC估计的方均根误差在1%左右，平均绝对误差减小至1%以内；当再融合1个超声信号频域特征与5个超声信号时频域变换特征作为输入时，在充电过程中，电池SOC估计的方均根误差小于0.85%，平均绝对误差小于0.58%；在放电过程中，电池SOC估计的方均根误差小于0.37%，平均绝对误差小于0.24%，验证了本文提出方法的有效性和准确性。

表4 三特征输入时锂离子电池SOC估计精度

Tab.4 Estimation accuracy of lithium-ion battery SOC with three features input

表5 五特征输入时锂离子电池SOC估计精度

Tab.5 Estimation accuracy of lithium-ion battery SOC with five features input

3.2.3 动态工况验证

为验证本文提出的方法在动态工况下的适用性，采用动态应力测试（Dynamic Stress Test, DST）工况进行验证。标准DST工况下每个循环可放出电池额定容量的1.25%，但是考虑到电池实际容量与额定容量的差异，采用77个DST循环对电池进行放电，共耗时462 min，电池放电过程中电压和电流如图13所示。在进行DST工况下电池SOC估计时，模型训练集大小为12×924，测试集大小与训练集大小相同。DST工况下锂离子电池的SOC估计结果如图14所示，DST工况下锂离子电池SOC估计精度见表6。可以看出，在DST工况下，电池SOC估计的方均根误差在1.46%以内，平均绝对误差在1.15%以内，证明了本文提出的锂离子电池SOC估计方法在动态工况下的准确性与适用性。

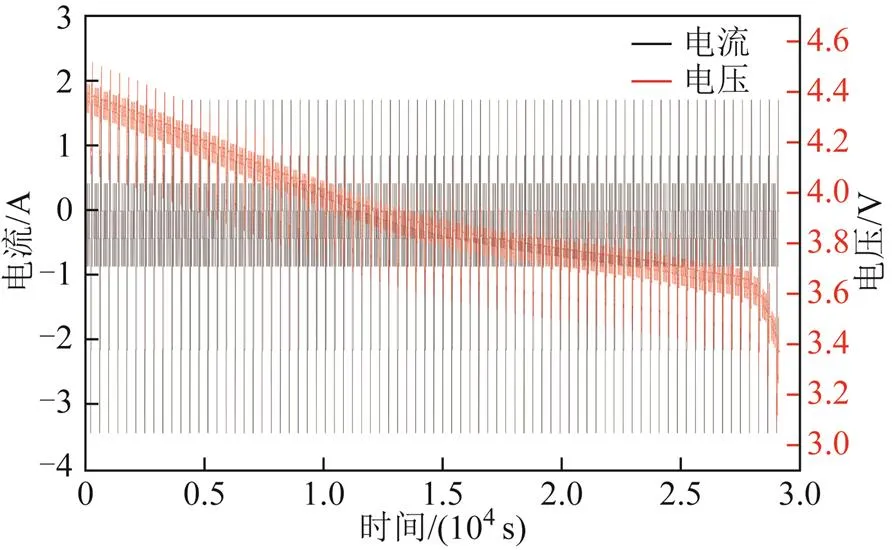
图13 DST工况下电池电压与电流曲线

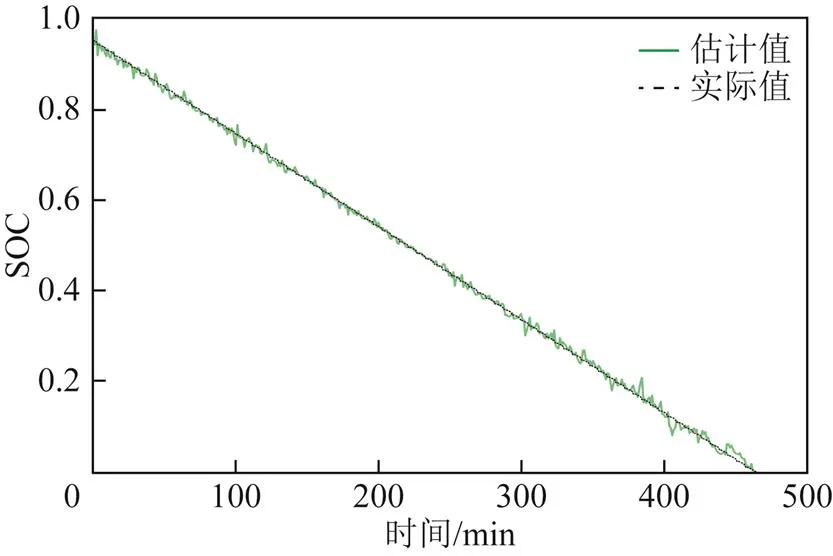
图14 DST工况下锂离子电池SOC估计结果

表6 DST工况下锂离子电池SOC估计精度

Tab.6 SOC estimation accuracy of lithium-ion battery under DST conditions

4 结论

针对传统方法利用电池电压、电流、温度等参数难以精确地估计电池SOC的问题，本文提出融合多维超声时频域特征的锂离子电池SOC估计方法。采用连续均匀分层介质模型分析了超声波在电池内部的传播特性，通过信号时频域分析对超声信号进行多维时频域特征提取，并结合LSTM神经网络建立了融合多维超声时频域特征的锂离子电池SOC估计模型，实现了电池SOC的精确估计。主要结论如下：

1）提取了超声信号时域特征、频域特征及时频域变换特征等多维超声时频域特征，得到了超声信号在不同尺度下的特征信息，利用超声特征可以表征电池充放电过程中内部的电化学过程，并确定了TOF、SA、m、CLI6、CLI7、CLI8、KU7和KU8八个超声时频域特征与电池SOC具有高相关性。

2）基于LSTM建立了融合多维超声时频域特征的锂离子电池SOC估计模型。结果表明，在电池充电过程中，SOC估计的方均根误差在0.85%以内，平均绝对误差在0.58%以内；在电池放电过程中，SOC估计的方均根误差在0.37%以内，平均绝对误差在0.24%以内，实现了电池SOC的精确有效估计。同时对比了不同特征作为输入时电池SOC的估计精度，实验结果表明，融合多维超声时频域特征可以有效地提高电池SOC估计精度，在动态工况下SOC估计的方均根误差在1.46%以内，平均绝对误差在1.15%以内，验证了方法的有效性和准确性。

本文提出的锂离子电池SOC估计方法在传统方法基础上，融合了反映电池内部动力学特性的多维超声时频域特征，在BMS中结合有效算法和策略可对电池SOC进行精确估计，电池局部信号数据的增加将有效地提高BMS的可靠性和准确性。同时，基于锂离子电池材料和结构的相似性，对LCO电池的研究基础可以继续在其他锂离子电池上应用，为其他锂离子电池的表征研究提供了依据。

[1] 李宁, 何复兴, 马文涛, 等. 基于经验模态分解的门控循环单元神经网络的锂离子电池荷电状态估计[J]. 电工技术学报, 2022, 37(17): 4528-4536.

Li Ning, He Fuxing, Ma Wentao, et al. State-of-charge estimation of lithium-ion battery based on gated recurrent unit using empirical mode decomposition[J]. Transactions of China Electrotechnical Society, 2022, 37(17): 4528-4536.

[2] Yang Bo, Wang Junting, Cao Pulin, et al. Classification, summarization and perspectives on state-of-charge estimation of lithium-ion batteries used in electric vehicles: a critical comprehensive survey[J]. Journal of Energy Storage, 2021, 39: 102572.

[3] Wang Zuolu, Feng Guojin, Zhen Dong, et al. A review on online state of charge and state of health estimation for lithium-ion batteries in electric vehicles[J]. Energy Reports, 2021, 7: 5141-5161.

[4] 王榘, 熊瑞, 穆浩. 温度和老化意识融合驱动的电动车辆锂离子动力电池电量和容量协同估计[J]. 电工技术学报, 2020, 35(23): 4980-4987.

Wang Ju, Xiong Rui, Mu Hao. Co-estimation of lithium-ion battery state-of-charge and capacity through the temperature and aging awareness model for electric vehicles[J]. Transactions of China Electrotechnical Society, 2020, 35(23): 4980-4987.

[5] 巫春玲, 胡雯博, 孟锦豪, 等. 基于最大相关熵扩展卡尔曼滤波算法的锂离子电池荷电状态估计[J]. 电工技术学报, 2021, 36(24): 5165-5175.

Wu Chunling, Hu Wenbo, Meng Jinhao, et al. State of charge estimation of lithium-ion batteries based on maximum correlation-entropy criterion extended Kalman filtering algorithm[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5165-5175.

[6] Bayati M, Abedi M, Gharehpetian G B, et al. Short-term interaction between electric vehicles and microgrid in decentralized vehicle-to-grid control methods[J]. Protection and Control of Modern Power Systems, 2019, 4(1): 1-11.

[7] Zheng Yuejiu, Ouyang Minggao, Han Xuebing, et al. Investigating the error sources of the online state of charge estimation methods for lithium-ion batteries in electric vehicles[J]. Journal of Power Sources, 2018, 377: 161-188.

[8] Shi Na, Chen Zewang, Niu Mu, et al. State-of-charge estimation for the lithium-ion battery based on adaptive extended Kalman filter using improved parameter identification[J]. Journal of Energy Storage, 2022, 45: 103518.

[9] 武龙星, 庞辉, 晋佳敏, 等. 基于电化学模型的锂离子电池荷电状态估计方法综述[J]. 电工技术学报, 2022, 37(7): 1703-1725.

Wu Longxing, Pang Hui, Jin Jiamin, et al. A review of SOC estimation methods for lithium-ion batteries based on electrochemical model[J]. Transactions of China Electrotechnical Society, 2022, 37(7): 1703-1725.

[10] 王义军, 左雪. 锂离子电池荷电状态估算方法及其应用场景综述[J]. 电力系统自动化, 2022, 46(14): 193-207.

Wang Yijun, Zuo Xue. Review on estimation methods for state of charge of lithium-ion battery and their application scenarios[J]. Automation of Electric Power Systems, 2022, 46(14): 193-207.

[11] 罗勇, 祁朋伟, 黄欢, 等. 基于容量修正的安时积分SOC估算方法研究[J]. 汽车工程, 2020, 42(5): 681-687.

Luo Yong, Qi Pengwei, Huang Huan, et al. Study on battery SOC estimation by ampere-hour integral method with capacity correction[J]. Automotive Engineering, 2020, 42(5): 681-687.

[12] Dang Xuanju, Yan Li, Jiang Hui, et al. Open-circuit voltage-based state of charge estimation of lithium-ion power battery by combining controlled auto-regressive and moving average modeling with feedforward-feedback compensation method[J]. International Journal of Electrical Power & Energy Systems, 2017, 90: 27-36.

[13] Shen Jiani, He Yijun, Ma Zifeng, et al. Online state of charge estimation of lithium-ion batteries: a moving horizon estimation approach[J]. Chemical Engineering Science, 2016, 154: 42-53.

[14] Popp H, Koller M, Keller S, et al. State estimation approach of lithium-ion batteries by simplified ultrasonic time-of-flight measurement[J]. IEEE Access, 2019, 7: 170992-171000.

[15] 刘素贞, 袁路航, 张闯, 等. 基于超声时域特征及随机森林的磷酸铁锂电池荷电状态估计[J]. 电工技术学报, 2022, 37(22): 5872-5885.

Liu Suzhen, Yuan Luhang, Zhang Chuang, et al. State of charge estimation of LiFePO4batteries based on time domain features of ultrasonic waves and random forest[J]. Transactions of China Electrotechnical Society, 2022, 37(22): 5872-5885.

[16] 张闯, 孙博, 金亮, 等. 基于声波时域特征的锂离子电池荷电状态表征[J]. 电工技术学报, 2021, 36(22): 4666-4676.

Zhang Chuang, Sun Bo, Jin Liang, et al. Characterization of the state of charge of lithium-ion batteries based on the time-domain characteristics of acoustic waves[J]. Transactions of China Electrotechnical Society, 2021, 36(22): 4666-4676.

[17] Hsieh A G, Bhadra S, Hertzberg B J, et al. Electrochemical-acoustic time of flight: in operando correlation of physical dynamics with battery charge and health[J]. Energy & Environmental Science, 2015, 8(5): 1569-1577.

[18] Chang Junjie, Zeng Xuefeng, Wan Taolei. Real-time measurement of lithium-ion batteries’ state-of-charge based on air-coupled ultrasound[J]. AIP Advances, 2019, 9(8): 085116.

[19] Ladpli P, Kopsaftopoulos F, Chang Fukuo. Estimating state of charge and health of lithium-ion batteries with guided waves using built-in piezoelectric sensors/actuators[J]. Journal of Power Sources, 2018, 384: 342-354.

[20] Davies G, Knehr K W, Van Tassell B, et al. State of charge and state of health estimation using electrochemical acoustic time of flight analysis[J]. Journal of the Electrochemical Society, 2017, 164(12): A2746-A2755.

[21] Ladpli P, Liu Chen, Kopsaftopoulos F, et al. Estimating lithium-ion battery state of charge and health with ultrasonic guided waves using an efficient matching pursuit technique[C]//2018 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Bangkok, Thailand, 2018: 1-5.

[22] Li Honggang, Zhou Zhenggan. Numerical simulation and experimental study of fluid-solid coupling-based air-coupled ultrasonic detection of stomata defect of lithium-ion battery[J]. Sensors, 2019, 19(10): 2391.

[23] 刘素贞, 饶诺歆, 张闯, 等. 基于LabVIEW的电磁超声无损检测系统的设计[J]. 电工技术学报, 2018, 33(10): 2274-2281.

Liu Suzhen, Rao Nuoxin, Zhang Chuang, et al. Design of electromagnetic ultrasonic nondestructive testing system based on LabVIEW[J]. Transactions of China Electrotechnical Society, 2018, 33(10): 2274-2281.

[24] 车畅畅, 王华伟, 倪晓梅, 等. 基于1D-CNN和Bi-LSTM的航空发动机剩余寿命预测[J]. 机械工程学报, 2021, 57(14): 304-312.

Che Changchang, Wang Huawei, Ni Xiaomei, et al. Residual life prediction of aeroengine based on 1D-CNN and Bi-LSTM[J]. Journal of Mechanical Engineering, 2021, 57(14): 304-312.

[25] 周世杰, 李顶根. 基于超声测量及神经网络的锂离子动力电池SOC估算[J]. 汽车工程学报, 2021, 11(1): 19-24.

Zhou Shijie, Li Dinggen. SOC estimation for lithium ion power batteries based on ultrasonic measurement and neural networks[J]. Chinese Journal of Automotive Engineering, 2021, 11(1): 19-24.

State of Charge Estimation of Lithium-Ion Batteries Fused with Multi-Dimensional Ultrasonic Time-Frequency Domain Features

Liu Suzhen1,2Chen Yunlong1,2Zhang Chuang1,2Jin Liang1,2Yang Qingxin1

（1. State Key Laboratory of Reliability and Intelligence of Electrical Equipment Hebei University of Technology Tianjin 300130 China2. Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability of Hebei ProvinceHebei University of Technology Tianjin 300130 China）

The state of charge (SOC) of lithium-ion batteries is an essential parameter of the battery management system. Accurately estimating the SOC of lithium-ion batteries is crucial for the safe operation of electric vehicles. However, SOC cannot be measured directly, and it can only be estimated by parameters related to the working state of the battery. Meanwhile, due to the highly nonlinear and time-varying characteristics of the battery, the accurate estimation of battery SOC has become a difficult issue. Conventional methods estimate the SOC by using battery voltage, current, temperature, and other parameters. However, the acquisition of these parameters depends on the measurement of electrode behavior. And they are susceptible to factors such as impedance and charge-discharge rate. Compared with conventional signals, ultrasonic signals can discriminate minor changes in the battery materials’ physical properties, so they can characterize the battery states accurately.At present, the research on estimating SOC by ultrasound only utilizes the time-domain features of ultrasonic signals, which lacks multi-dimensional analysis. Moreover, due to the nonlinear and non-stationary characteristics of ultrasonic signals, using the time-domain features cannot reflect the changes of ultrasonic signals at different scales, which will reduce the accuracy of SOC estimation. In order to solve the above problems, this paper proposes a lithium-ion battery SOC estimation method that integrates multi-dimensional ultrasonic time-frequency domain features. Multi-dimensional ultrasonic time-frequency domain features which have high correlations with SOC are extractedthrough joint time-frequency domain analysis of signals. The lithium-ion battery SOC estimation model is proposed by long-short-term memory neural network (LSTM), which realizes the accurate estimation of battery SOC.

Firstly, the propagation process of ultrasonic waves in the battery was studied through the continuous uniform layered medium model. The influence of the battery materials’ physical properties on the ultrasonic propagation characteristics was analyzed.Secondly, the ultrasonic testing platform for lithium-ion batteries was built and the multi-dimensional ultrasonic time-frequency domain features were extracted. Based on the ultrasonic features, the electrochemical process inside the battery was explained. Finally, considering the special processing ability of LSTM for time series data, the SOC estimation model of lithium-ion batteries fused with multi-dimensional ultrasonic time-frequency domain features was proposed by LSTM. The effects of different fusion features on SOC estimation accuracy were compared.

Experimental results show that the accuracy of SOC estimation can be effectively improved by the integration of multi-dimensional ultrasonic time-frequency features. During battery charging and discharging, the root mean square error of SOC estimation is within 0.85% and 0.37% respectively, and the mean absolute error is within 0.58% and 0.24%. At the initial stage of battery charging and discharging, the error of SOC estimation is relatively large. But as the process goes on, the estimation error decreases gradually, which also reflects that LSTM can capture the change of SOC and its dependence on battery historical states through time series data.In order to verify the applicability of this method under dynamic conditions further, dynamic stress test (DST) conditions are used for verification. The results show that under DST conditions, the root mean square error of SOC estimation is within 1.46%, and the average absolute error is within 1.15%, which verifies the effectiveness and accuracy of the method.

Lithium-ion batteries, state of charge, ultrasonic testing, long-short-term memory neural network, multi-dimensional ultrasonic features

TM911

10.19595/j.cnki.1000-6753.tces.221046

中央引导地方科技发展项目（216Z4406G）和清华大学国家重点实验室开放课题（SKLD21KZ04）资助。

2022-06-0

2022-09-19

刘素贞 女，1969年生，博士，教授，博士生导师，研究方向为工程电磁场与磁技术。E-mail：szliu@hebut.edu.cn（通信作者）

陈云龙 男，1998年生，硕士研究生，研究方向为锂离子电池超声检测。E-mail：202021401050@stu.hebut.edu.cn

（编辑 李冰）