基于锂电池模型和分数阶理论的SOC-SOH联合估计

赵靖英 胡 劲 张雪辉 张文煜

基于锂电池模型和分数阶理论的SOC-SOH联合估计

赵靖英1胡 劲1张雪辉1张文煜2

（1. 省部共建电工装备可靠性与智能化国家重点实验室（河北工业大学） 天津 300130 2. 国网冀北张家口风光储输新能源有限公司 张家口 075000）

基于锂电池荷电状态（SOC）和健康状态（SOH）的耦合关系，设计了SOC-SOH联合估计系统。首先，构建锂电池等效电路模型和自适应扩展卡尔曼滤波（AEKF）算法，进行锂电池SOC估计；其次，建立锂电池分数阶模型，设计模糊控制器辨识分数阶模型参数，基于分数阶模型参数和电池充电工况确立健康因子，引入麻雀搜索算法（SSA）改进反向传播神经网络（BPNN），进行锂电池SOH估计；然后，集成SOC与SOH估计方法，设计联合估计系统；最后，设计锂电池老化实验、动态应力测试（DST）和US06动态实验方案，对比分析不同工况下不同算法的SOC-SOH联合估计效果。结果表明，基于提出的SOC-SOH联合估计方法，估计误差小于1%，具有良好的估计特性。

锂电池 分数阶模型 健康因子 荷电状态 健康状态

0 引言

对于电池管理系统（Battery Management System, BMS），锂电池荷电状态（State of Charge, SOC）和健康状态（State of Health, SOH）是体现系统运行特性的关键状态变量[1]。SOC定义为电池当前电荷量与最大容量之比[2]，反映了电池当前电荷量的存储状态；SOH通常由当前最大容量或内阻来定义[3]，反映电池全生命周期尺度下的老化状态。

对锂电池SOC的准确估计，有助于提高电池能量利用率，防止过充电和过放电。工程实际中普遍采用安时积分法进行锂电池SOC估计，但此方法无法克服累计误差[4]。基于卡尔曼滤波（Kalman Filter, KF）算法的SOC估计方法也得到普遍关注[5]。文献[6-7]利用两个扩展卡尔曼滤波器（Extended Kalman Filter, EKF）同步估计电池模型参数和SOC，利用新息和残差优化噪声协方差，提高了动态工况下SOC估计的精度。文献[8]利用模糊控制器调控噪声协方差，研究自适应扩展卡尔曼滤波（Adaptive Extended Kalman Filter, AEKF）算法，实现动态工况下SOC估计的快速收敛。文献[9]利用Huber-M方法改进KF算法，并将门控循环单元神经网络的输出量作为观测值，提高了锂电池SOC估计的精度和收敛速度。文献[10]考虑温度影响，提出改进的锂电池双极化模型，实现了添加温度变量的SOC精确估计。

锂电池SOH的精确估计有利于系统及时做出预警，保证长期安全运行。国内外研究中，SOH估计方法分为直接测量法、基于数据驱动和基于模型的估计方法等。直接测量法是在实验条件下利用库伦计数法直接测量锂电池容量[11]，或对电池施加交流激励，通过频谱特征分析计算SOH[12-13]。直接测量法精度较高，但脱离实验室条件难以进行。基于数据驱动的SOH估计方法是利用电池老化的外部特征作为健康因子（Health Factor, HF），基于机器学习等手段，构建HF与SOH的非线性映射关系，实现锂电池SOH估计[14]。文献[15]在电池充电曲线中提取8个健康因子，利用相关向量机建立SOH估计模型。文献[16]利用容量增量分析法提取健康因子，根据高斯回归过程建立SOH估计模型，实现SOH的精确估计。文献[17]将电池电压、电流、温度的时间序列作为健康因子，通过卷积神经网络构建SOH估计模型。基于模型的SOH估计方法是通过建立经验模型、等效电路模型或电化学模型来拟合电池外特性，辨识模型参数后进行锂电池SOH估计。文献[18]通过建立锂电池准二维电极模型，刻画锂电池内部反应机理，评估锂电池SOH。文献[19]将锂电池SOH指数经验模型与高斯过程回归结合，实现锂电池SOH预测。文献[20]离线分析锂电池交流阻抗谱，计算特征阻抗进行锂电池SOH估计。文献[21]利用无迹卡尔曼滤波算法估计锂电池二阶RC模型的欧姆内阻，基于欧姆内阻进一步估计锂电池SOH。

锂电池SOH与SOC之间存在耦合关系，在采用容量定义SOH时，随着SOH降低，锂电池最大容量发生改变，若不对容量参数进行修正，将导致SOC估计结果产生偏差。因此有学者提出SOC-SOH联合估计。文献[22]提出利用循环神经网络并行工作的策略，实现锂电池SOC和SOH同步估计。文献[23]利用KF算法，在估计锂电池SOC的同时，通过最小二乘法进行容量观测，实现锂电池SOC和SOH的联合估计。文献[24]在门控循环单元循环神经网络估计锂电池SOC的基础上，结合卷积神经网络估计锂电池SOH，建立SOC-SOH联合估计系统。

基于锂电池等效电路模型和KF算法估计锂电池SOC已取得了较好应用，但参数过多与估计精度低的问题限制了等效电路模型在SOH估计方法研究领域的应用，SOC-SOH联合估计的时效性有待进一步提升。本文首先利用锂电池二阶RC模型结合AEKF算法实现锂电池SOC估计；其次基于分数阶微积分理论建立锂电池分数阶模型，根据分数阶模型参数和电池充电容量与时间的关系确立健康因子，引入麻雀搜索算法（Sparrow Search Algorithm, SSA）优化反向传播神经网络（Back Propagation Neural Network, BPNN），基于SSA-BPNN进行锂电池SOH估计；然后修正电池容量，提出SOC-SOH联合估计方法；最后设计锂电池老化和动态实验方案，验证锂电池SOC-SOH联合估计方法的有效性。

1 锂电池SOC估计方法

1.1 锂电池等效电路模型

锂电池SOC为短期变量，卡尔曼滤波算法中需利用状态方程矩阵相乘和求逆运算，迭代获取SOC估计值。锂电池二阶RC等效电路模型[6]如图1所示，输出时域表达式为二阶指数形式，状态方程简单，可降低计算量，适用于SOC的高频次短时计算，同时引入锂电池端电压实测值对模型输出值进行修正，满足SOC估计精度需求。

图1 锂电池等效电路模型

根据图1可构建系统状态方程为

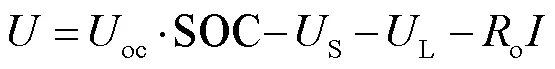
式中，、分别为电池端电压、电流；oc为开路电压；L和S分别为电化学极化内阻和浓差极化内阻；S和L分别为S和L端电压；s和l为时间常数；c为电池最大容量；Δ为采样间隔；为离散时间。

1.2 基于AEKF算法估计锂电池SOC

EKF作为KF算法之一，常被用于非线性系统状态估计[4]。基于EKF算法进行锂电池SOC估计时，噪声协方差一般设置为固定值。但考虑复杂工况条件下，噪声协方差会发生动态变化，需设计噪声协方差自适应策略，利用电池端电压实测值和模型预测值计算系统过程误差，根据卡尔曼增益，获取动态噪声协方差。因此，构建AEKF算法估计锂电池SOC，具体如下：

将式（1）和式（2）进行变换得到

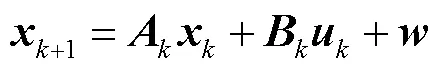
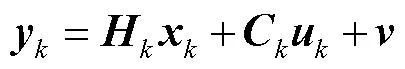
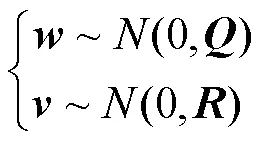
式中，、、、分别为系统状态转移矩阵、输入矩阵、输出矩阵和前馈矩阵；和分别为系统状态向量和输出值；k为系统输入；、分别为系统过程噪声及其协方差矩阵；、分别为系统测量噪声及其协方差矩阵；(·)为正态分布。AEKF递推过程如下。

1）时间更新

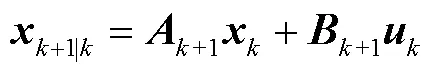
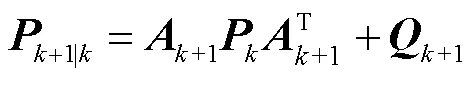
式中，为时刻的系统误差协方差矩阵；下标“+1|”表示基于时刻系统状态对+1时刻系统状态的递推结果。

2）测量更新

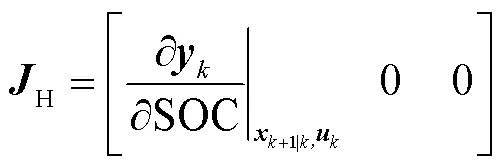
式中，mea为电池端电压测量值；+1为递推的卡尔曼增益；e为单位矩阵；H为一阶偏导向量。

3）进行误差协方差自适应计算

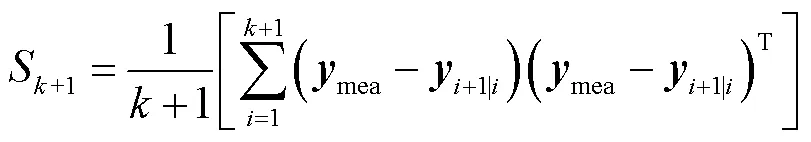
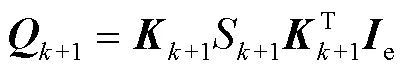
式中，S+1为+1时刻的累计误差。

2 分数阶模型建立及健康因子提取

定义锂电池SOH为当前最大容量c与额定容量rated之比，即

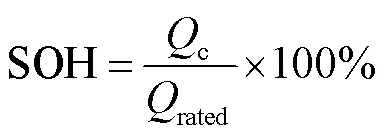
2.1 锂电池分数阶模型

锂电池RC模型的精度与RC环节的数量成正比[25]，提升精度的同时会导致模型参数量过多、参数物理意义模糊等问题。文献[26]指出锂电池极化的分数阶特征。分数阶模型时域表达式具有无穷级数性质，虽然计算量大于整数阶模型，但应用于SOH估计低频计算，能够以更少参数和更高精度准确地描述锂电池极化与SOH的相关性，可解决整数阶模型精度和参数过多之间的矛盾。因此，提出利用分数阶微积分理论优化RC模型。

将二阶RC模型扩展至阶，则阶等效电路模型如图2所示。

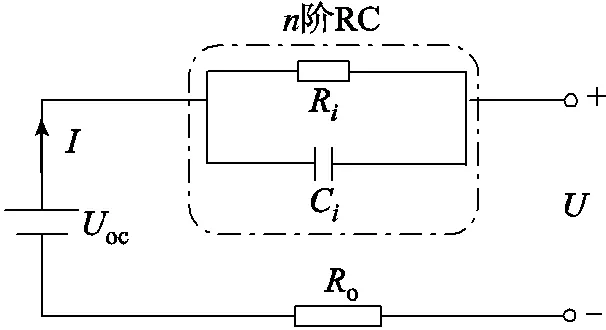
图2 n阶等效电路模型

恒流脉冲充、放电情况下，个RC环节可视为线性定常系统，转换至复频域可得到传递函数为

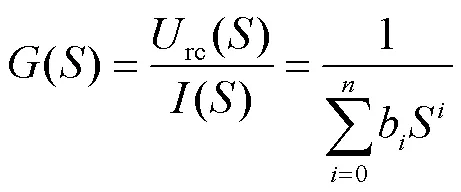
式中，rc为RC串联模块端电压；b为传递函数化简后的分母项系数。

根据Oustaloup滤波器[27]原理，高阶整数阶传递函数可等效为分数阶传递函数。Oustaloup滤波器数学模型为

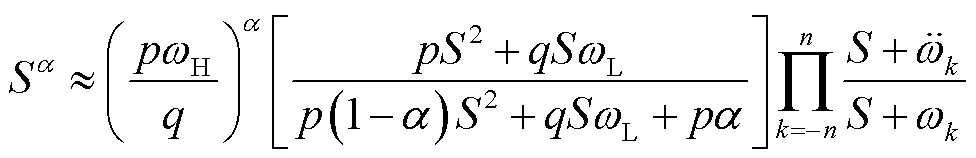
式中，和均为加权参数；为分数阶算子阶次，可取(0, 1)内的有理数，本文取0.4；H和L分别为频段上、下限，本文选择的频段为10-8～108rad/s；模型阶次即为滤波器阶次。

将式（15）所示的整数阶传递函数等效为式（18）所示的分数阶传递函数，即可得到一个高精度、低参数维数的锂电池分数阶模型。

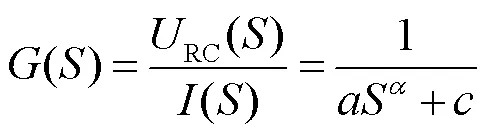
式中，RC为分数阶传递函数模块端电压；和为分数阶传递函数分母项系数。

2.2 健康因子提取

锂电池SOH难以直接测量，需提取与SOH相关性较强的健康因子，间接地估计SOH。充电电流与时间积分是反映锂电池容量信息的直接方法，因此充电时间可作为估计SOH的健康因子，但实际应用中，人为因素导致锂电池初始充电电量不固定，完整充电时间难以测量。综合考虑，选择以锂电池电量20%为起始计时点，至恒流充电结束的时间c作为健康因子。

锂电池分数阶模型式（18）反映了锂电池极化特性，选择其中的、参数作为健康因子，和的采样窗口设置为在锂电池满电状态下恒流放电0～s。

为了量化c、、三个健康因子与SOH的相关程度，采用Spearman公式计算相关系数，即

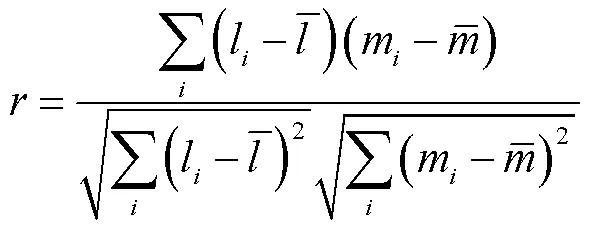
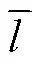
2.3 分数阶模型参数辨识

针对锂电池分数阶模型参数、，提出一种在恒流脉冲激励下，基于模糊控制器的时域辨识方法。

引入分数阶微积分定义式得到

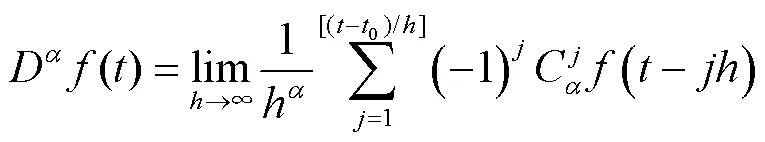
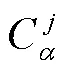
分数阶拉氏反变换公式为

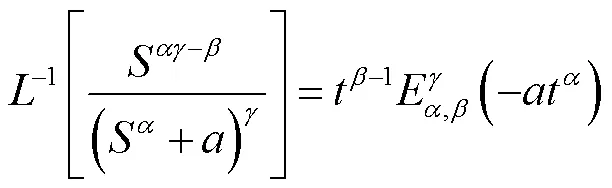
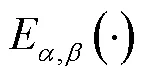
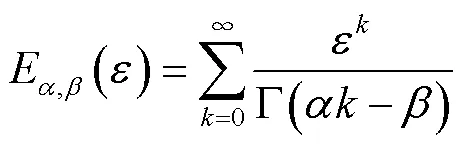
其中，Gamma函数定义为

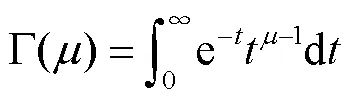
当输入为阶跃响应时，利用式（20）～式（24）对式（18）进行拉式反变换，将第一个采样点记为0时刻，则、反映了RC的时域变化率，可得到分数阶模块端电压时域表达式为

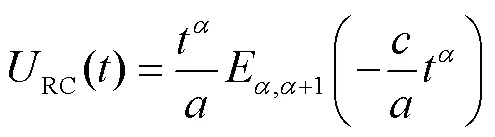
在采样窗口内建立端电压拟合关系式为

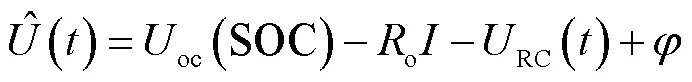
采样窗口内的电压拟合误差表示为

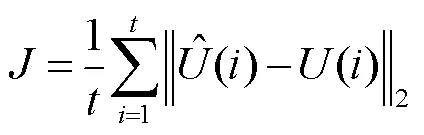
设计模糊控制器辨识参数a、c，其原理如图3所示，主要由六部分构成：①计算控制器的输入ΔU；②参数模糊化，包括论域和隶属函数；③根据经验制定的知识库；④模糊推理算法；⑤反模糊化，将模糊输出量转化为实际控制量a、c；⑥拟合误差判定。

以采样窗口内的分数阶模型输出和实测电压做差的Δ作为输入量，以参数、作为输出量。Δ的论域划分为五个等级：N+表示较大负值；N表示负值；ZS表示小；P表示正值；P+表示较大正值。采样窗口时长论域分为两个等级：A表示调整参数；C表示调整参数。、迭代步长论域分为五个等级：BN表示大步长递减；MN表示中步长递减；Z表示小步长随机增减；MP表示中步长递增；BP表示大步长递增。输入输出隶属函数如图4所示。

模糊控制器辨识参数原理为：

图4 输入输出隶属函数

3）重心法去模糊化，当＜时，输出。不大于端电压测量精度的量级。

3 锂电池SOC-SOH联合估计

3.1 SSA-BPNN估计锂电池SOH

BPNN的权重初值具有随机性，训练过程中易陷入局部最优解。可利用SSA[28]优化BPNN权重初值，得到权重全局最优解；再根据SSA-BPNN模型建立健康因子与SOH的非线性映射关系。

构建如图5所示的BPNN全连接层神经网络，输入层节点个数为3，输出层节点个数为1；隐含层数量为2，隐含层节点个数分别为5和3。设为BPNN各层之间连接权重构成的麻雀种群矩阵，矩阵维数为×，表示个麻雀个体，每个个体包含维BPNN初始参数。

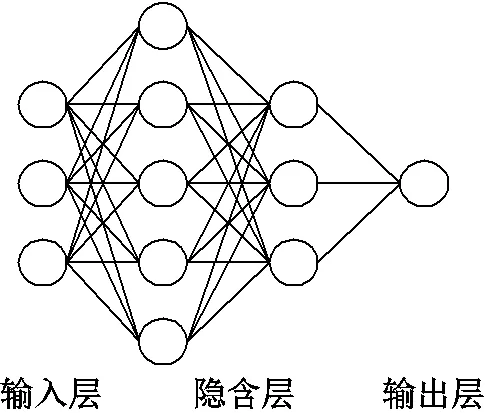
图5 反向传播神经网络

随机初始化麻雀种群矩阵，利用输出误差构建适应度函数为

式中，input和output分别为BPNN的输入和输出的目标值。

SSA-BPNN权重优化流程如图6所示，当达到种群最大进化次数时，对比选择输出误差最低的麻雀种群，获取最优权重初值。

图6 SSA-BPNN权重优化流程

3.2 SOC-SOH联合估计框架

锂电池SOC与SOH存在耦合关系，随着电池老化，SOH降低，c逐渐减小，导致放电倍率实际值偏高，影响SOC估计精度。准确地估计锂电池SOH，可保证锂电池生命周期内的SOC估计精度；同时，准确地估计SOC能够确保提取有效的健康因子，提升锂电池SOH估计精度。

SOC-SOH联合估计系统框架如图7所示，首先进行SSA-BPNN的离线训练；传感器采集电池电压、电流数据后，辨识二阶RC模型参数；再将模型参数导入式（1）和式（2），结合AEKF估计锂电池SOC；采样窗口内，模糊控制器辨识锂电池分数阶模型参数、；SSA-BPNN算法根据输入的参数c、、估计锂电池SOH；最后利用SOH估计值计算c，修正AEKF中c的值。

图7 锂电池SOC-SOH联合估计系统框架

4 实验验证与分析

为了验证算法的有效性，选取8枚18650三元锂电池作为实验对象，编号为1～8，额定容量为1 800 mA·h，最高电压为4.2 V，截止电压为2.5 V。电池测试平台（CT-4008T-5V12A）如图8所示。在室温下进行锂电池循环老化实验，采样间隔为1 s。

图8 电池测试平台

设计三套实验方案如下：

方案一：采用标准恒流-恒压充电方式，再通过1.1倍率放电至截止电压，当锂电池最大容量衰减至80%时停止实验。

方案二：使用0.25、0.5、1、1.25、2等多种电流倍率组合设计动态应力测试（Dynamic Stress Test, DST），验证城市普通路况下SOC估计方法的有效性。DST输入电流激励如图9所示。

方案三：根据美国环境保护局（Environmental Protection Agency, EPA）标准，设计锂电池US06实验方案，电流激励如图10所示，验证高速度、高加速度极端路况下SOC估计方法的有效性。

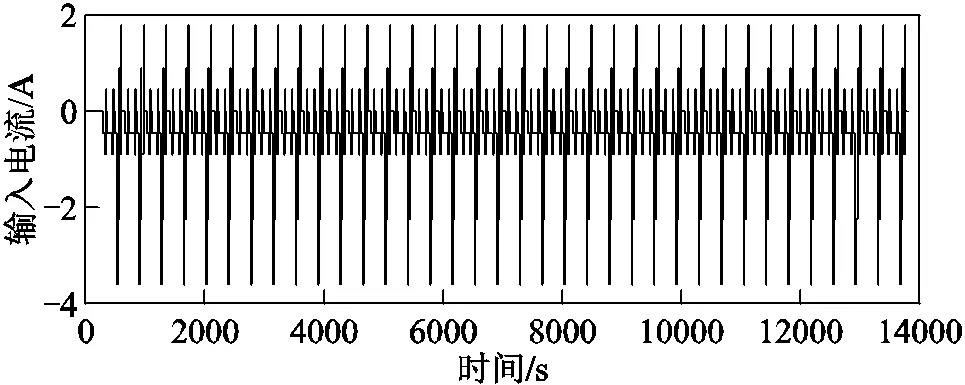
图9 DST输入电流激励

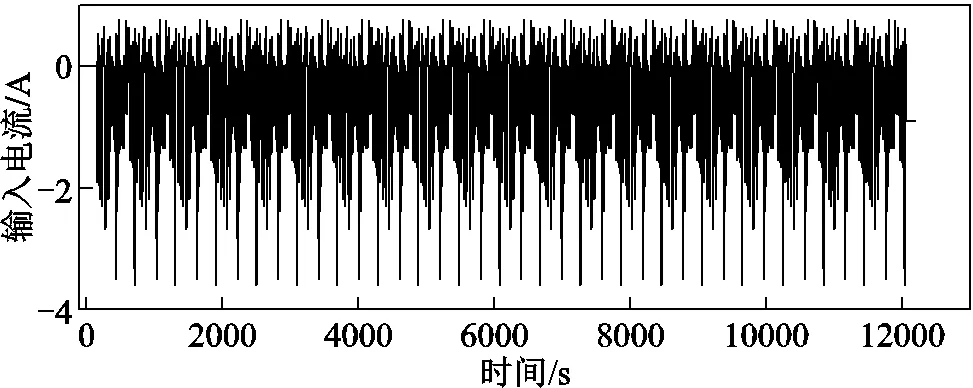
图10 US06实验电流激励

4.1 SOC估计方法验证

针对锂电池不同工况下的实验方案，利用遗忘因子递推最小二乘法（Recursive Least Squares with Forgetting Factor, FFRLS）辨识二阶RC模型参数[9]，结果如图11和图12所示。在DST、US06工况下，基于参数辨识结果的模型输出误差小于39.4 mV。

图11 DST实验参数辨识结果

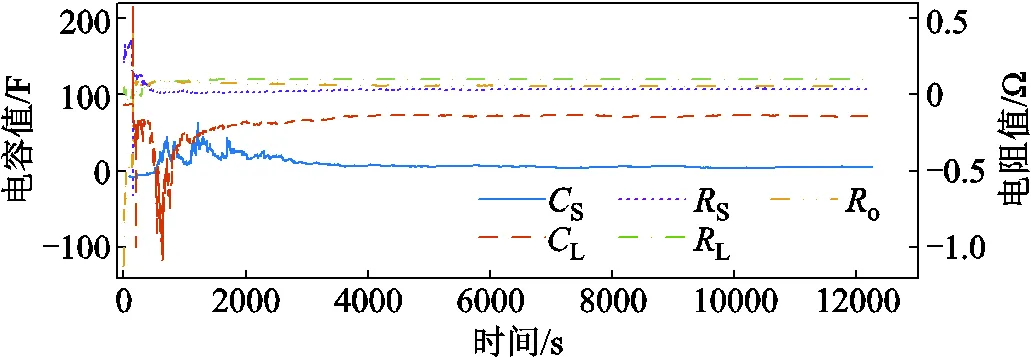
图12 US06实验参数辨识结果

在两种工况下，分别利用AEKF与EKF进行锂电池SOC估计，结果如图13和图14所示。各算法估计SOC的最大误差（Maximum Error, ME）、平均绝对误差（Mean Absolute Error, MAE）、方均根误差（Root Mean Squared Error, RMSE）见表1和表2。DST和US06工况下，基于EKF算法估计SOC时的ME均超过3%，而基于AEKF算法估计SOC时的ME均保持在1%以内，表明复杂工况下AEKF算法具有较强的鲁棒性。其中，US06工况下，基于EKF算法估计SOC时的MAE和RMSE分别为1.35%和1.96%，而基于AEKF算法估计SOC时的MAE和RMSE仅为0.32%和0.38%，表明AEKF算法具有较高的SOC估计精度。

图13 DST工况下SOC估计结果对比

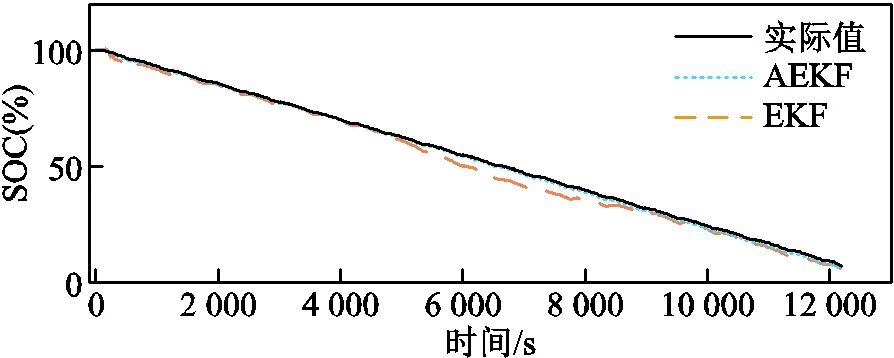
图14 US06工况下SOC估计结果对比

表1 DST工况下SOC估计误差

Tab.1 The errors of SOC estimation under DST

表2 US06工况下SOC估计误差

Tab.2 The errors of SOC estimation under US06

4.2 健康因子相关性验证

提取健康因子c、、，并验证其与SOH的相关性。随着锂电池逐渐老化，充电电压变化如图15所示。在锂电池端电压达到4.2 V之前采用恒流充电方式；当电池端电压达到4.2 V后，转换为恒压充电方式。图15中，当锂电池端电压处于区间[3.5 V, 3.8 V]时，实际应用中，该区间内锂电池电量较低，充电操作较为频繁，且充电初始电量具有随机性。为了确定c的初始计时点，以充电阶段SOC达到20%的时刻作为初始时刻，开始c的计时。根据式（19）计算得到健康因子c与SOH的Spearman相关系数达到0.96以上，表明两者具有较强相关性。

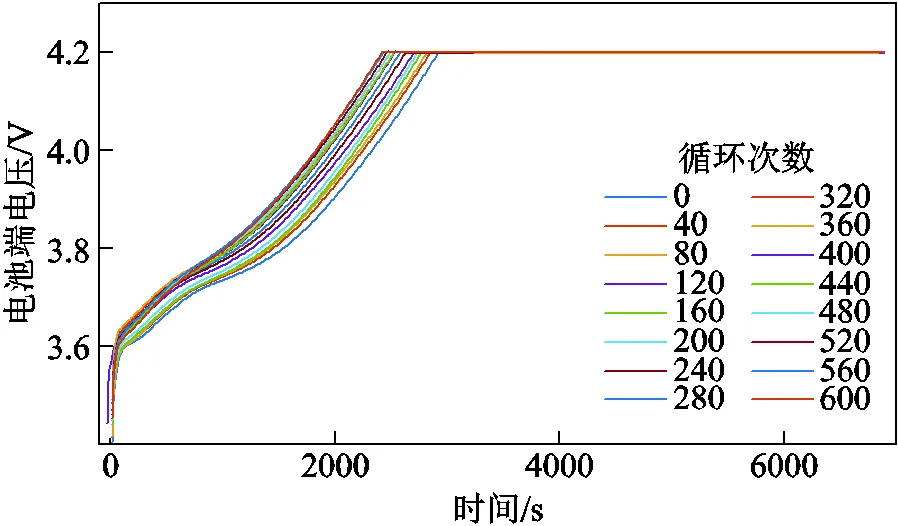
图15 电池老化过程充电电压

随着锂电池逐渐老化，恒流放电电压变化如图16所示。随着循环次数递增，锂电池外特性发生改变，在[0 s, 100 s]内端电压曲线的斜率逐渐减小，[100 s, 300 s]内斜率绝对值增大，在2 500 s后迅速达到截止电压。将、采样窗口设置为[0 s, 300 s]，可以统一采样窗口上限，缩短采样时间，符合实际应用需求。

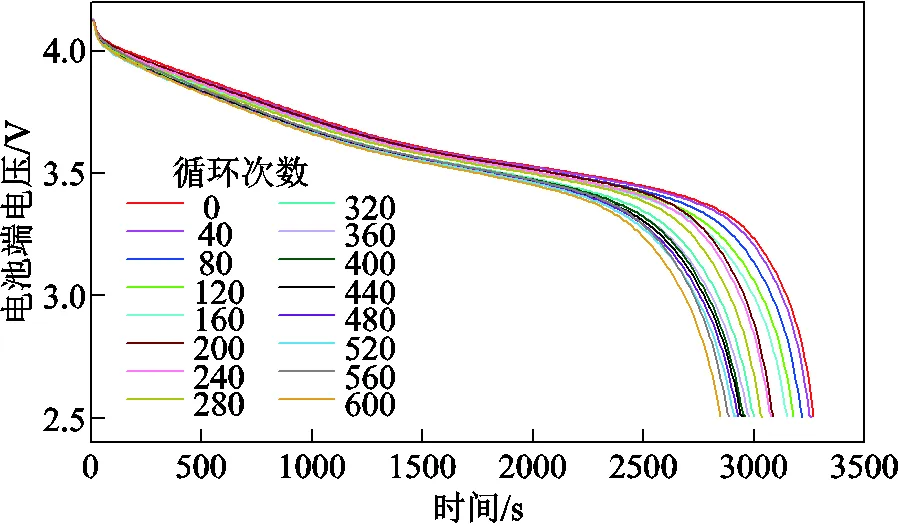
图16 电池老化过程放电电压

在采样窗口内获取锂电池分数阶模型参数、，初值选取[30, 100]和[5, 10]内的有理数。对比恒流脉冲条件下的二阶RC模型输出精度与分数阶模型输出精度，结果如图17所示，各项误差见表3。二阶RC模型在区间[0 s, 50 s]的电压输出值与实际值最大误差为27 mV，分数阶模型的最大误差仅为0.15 mV，精度远高于二阶RC模型，能够充分体现锂电池的极化特性。

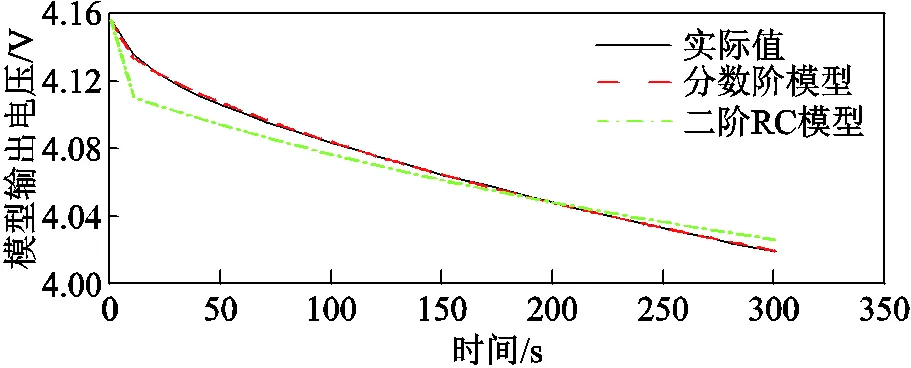
图17 锂电池模型精度对比

表3 模型拟合误差

根据式（19）计算得到、与SOH的Spearman相关系数均达到0.95以上，可见、与SOH均具有较强相关性。

4.3 SOC估计精度对SOH估计的影响

将8枚锂电池分为两组：1～6号电池作为训练集，用于SSA-BPNN离线训练；7、8号电池作为验证集。训练集中，c根据SOC实际值获得：利用实验平台测量电池充电电量，得到SOC实际值，当锂电池SOC实际值大于或等于20%时开始c的计时。

以SSA-BPNN训练过程的适应度表示训练误差，种群适应度曲线如图18所示，可见种群进化初期适应度大于1.5%；随着种群变化，训练效果逐渐增强，种群数量为26时达到最佳适应度。

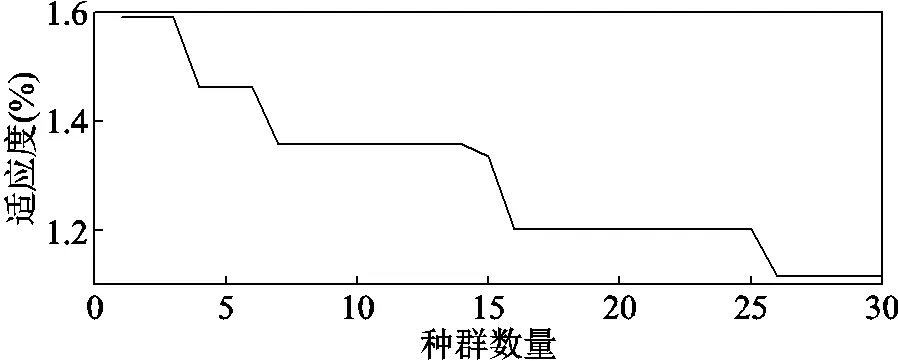
图18 种群适应度曲线

非实验条件下，验证集的c只能根据SOC估计值得到，即基于充电阶段SOC估计值达到20%时来获取c。恒流恒压（Constant Current Constant Voltage, CCCV）充电工况下的SOC估计结果对比如图19所示，误差见表4。由于AEKF算法和EKF算法的SOC估计误差最大值分别为0.20%和2.23%，不同SOC估计精度会影响c初始测量点定位精度，进而影响c测量精度，但总体误差不大。

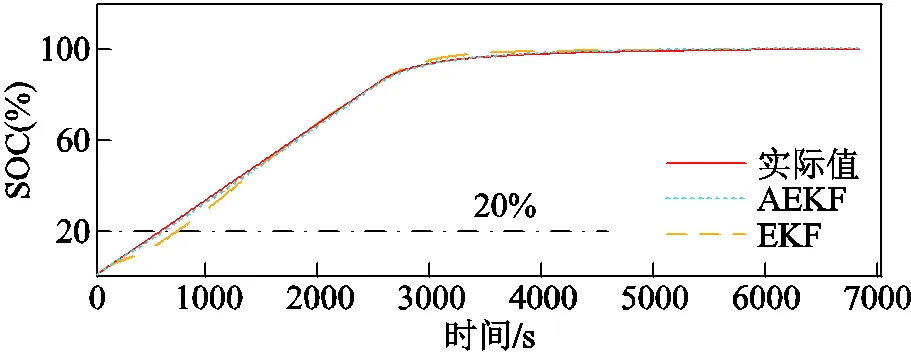
图19 CCCV工况下的SOC估计结果对比

表4 CCCV工况下SOC估计误差

Tab.4 The errors of SOC estimation under CCVC

对比基于AEKF和EKF获取c时的SOH估计精度，结果如图20和图21所示。图中，ΔSOH表示SOH估计值与真实值的相对误差；验证集1表示基于AEKF获取c时的SOH估计结果；验证集2表示基于EKF获取c时的SOH估计结果。由图20和图21可知，验证集1最大误差小于1%，验证集2最大误差超过2%。结果表明，准确估计SOC能够提高SOH估计精度。

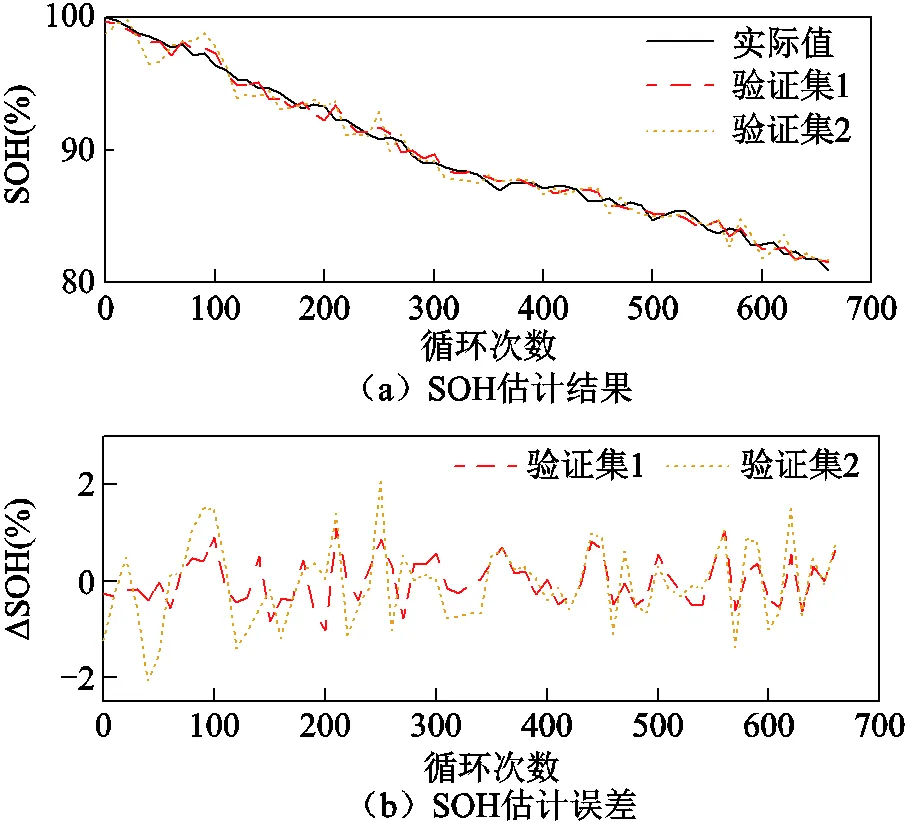
图20 7号电池SOH估计结果和误差

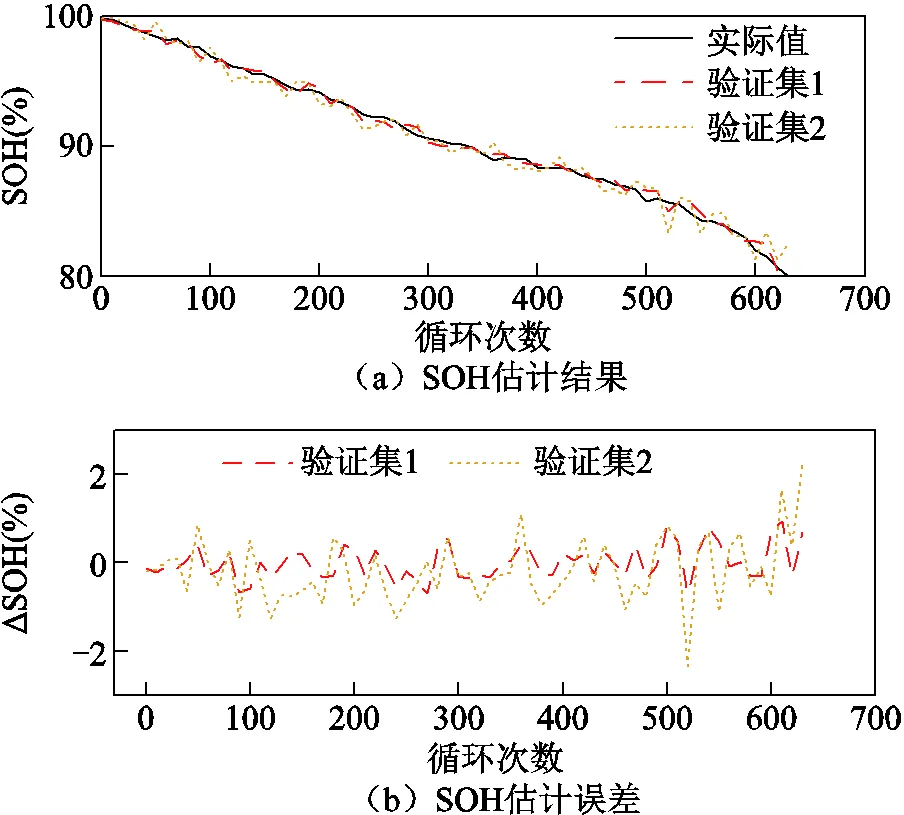
图21 8号电池SOH估计结果和误差

4.4 SOH估计精度对SOC估计的影响

电池老化后容量降低，引入SOC-SOH联合估计方法，基于式（14）和SOH估计值修正c，利用AEKF算法重新估计SOC，降低SOC估计误差。选取处于老化状态的7、8号电池，其实际容量由1 800 mA·h分别衰退至1 485 mA·h和1 445 mA·h。此时，根据SOH估计值，将7、8号电池的c分别修正为1 492.4 mA·h和1 456.2 mA·h。基于c修正前后的数值设置，利用AEKF算法进行SOC估计，不同工况下两枚电池的SOC估计结果如图22～图25所示。未修正c时，两枚锂电池SOC估计最大误差超过22%；而联合估计方法修正c后，两枚锂电池SOC估计最大误差均小于1%，SOC估计精度并未随电池老化程度加深而变差，时效性较强。

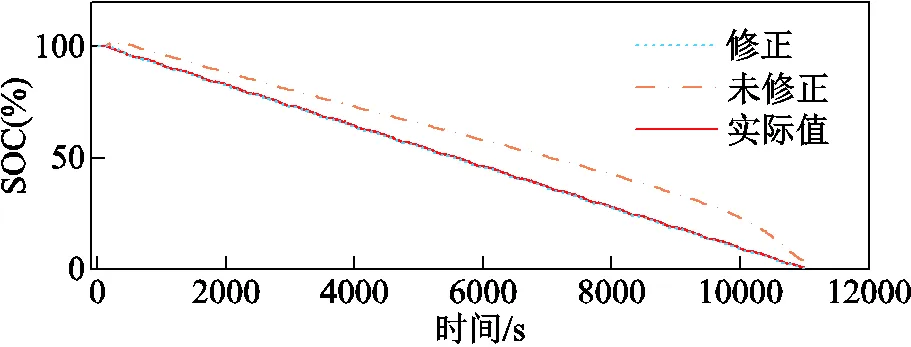
图22 7号电池US06工况下的SOC估计结果

图23 8号电池US06工况下的SOC估计结果

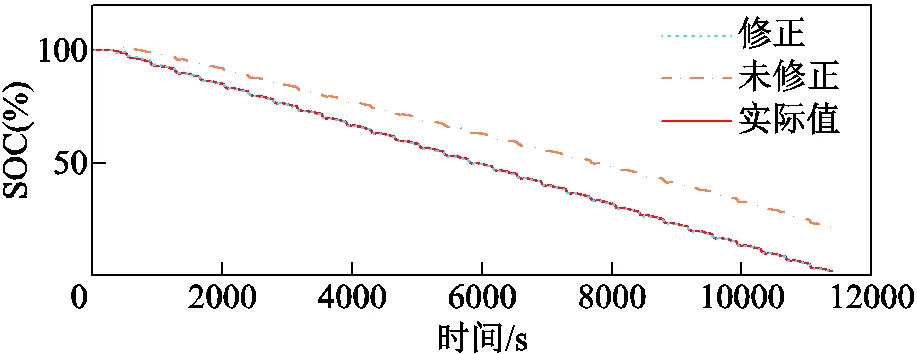
图24 7号电池DST工况下的SOC估计结果

图25 8号电池DST工况下的SOC估计结果

SOH估计误差影响c的修正精度。以8号电池为例，SOH实测值为80.3%，实测容量为1 445.4 mA·h。基于图21中的两组SOH估计值来修正c，取两组ΔSOH分别为0.7%和2.2%，可得到修正后的c分别为1 456.2 mA·h和1 477.3 mA·h。对比不同ΔSOH时基于AEKF算法的SOC估计精度，结果如图26和图27所示。基于ΔSOH=0.7%时，SOC估计误差最大值小于1%；基于ΔSOH=2.2%时，SOC估计误差最大值小于1.2%。结果表明，基于AEKF算法，ΔSOH对SOC估计精度产生的影响较小，联合算法具有较高的鲁棒性。

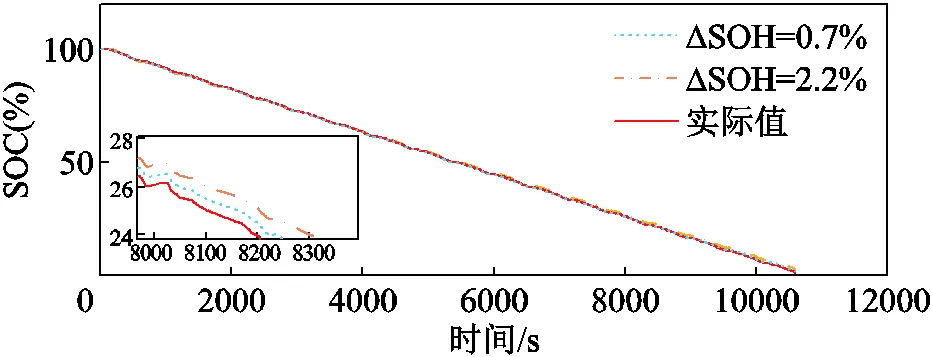
图26 SOH精度对US06工况下SOC估计结果的影响

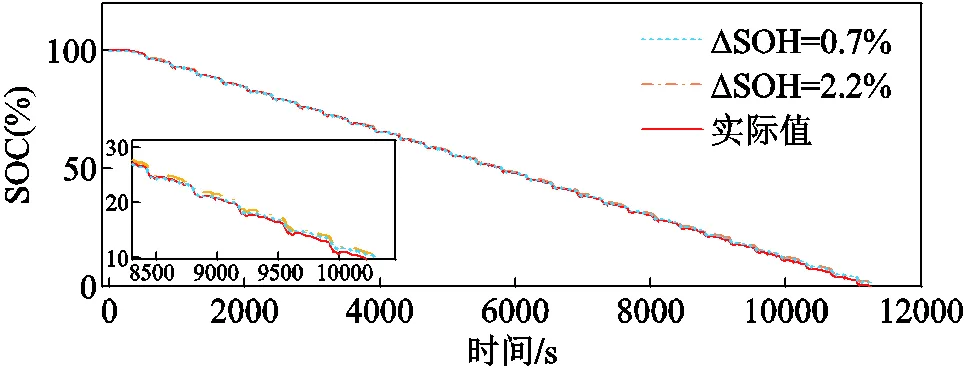
图27 SOH精度对DST工况下SOC估计结果的影响

5 结论

本文结合二阶RC模型和AEKF算法构建了锂电池SOC估计方法；利用分数阶微积分理论改进了锂电池二阶RC模型，将锂电池分数阶模型应用于SOH估计；构建了基于SSA-BPNN的锂电池SOH估计模型，设计了一种基于锂电池模型和分数阶理论的SOC-SOH联合估计系统。得到如下结论：

1）通过老化和动态实验设计，在不同工况下论证了基于AEKF算法的SOC估计精度优势和鲁棒性。

2）提取了健康因子，计算得到健康因子与SOH的相关系数均高于0.95，验证了健康因子与SOH的相关性。

3）对锂电池SOC估计与SOH估计的相互影响关系进行分析，结果表明，基于本文所提出的SOC-SOH联合估计系统，不同动态工况下，锂电池SOC估计最大误差均低于1%，不同实验电池的SOH估计最大误差均低于1%，验证了SOC-SOH联合估计方法的有效性，且具有良好的精度和时效性。

[1] 朱丽群, 张建秋. 一种联合锂电池健康和荷电状态的新模型[J]. 中国电机工程学报, 2018, 38(12): 3613-3620, 21.

Zhu Liqun, Zhang Jianqiu. A new model of jointed states of charge and health for lithium batteries[J]. Proceedings of the CSEE, 2018, 38(12): 3613-3620, 21.

[2] Li Chaoran, Xiao Fei, Fan Yaxiang. An approach to state of charge estimation of lithium-ion batteries based on recurrent neural networks with gated recurrent unit[J]. Energies, 2019, 12(9): 1592.

[3] Dai Houde, Zhao Guangcai, Lin Mingqiang, et al. A novel estimation method for the state of health of lithium-ion battery using prior knowledge-based neural network and Markov chain[J]. IEEE Transactions on Industrial Electronics, 2019, 66(10): 7706-7716.

[4] 刘芳, 马杰, 苏卫星, 等. 基于自适应回归扩展卡尔曼滤波的电动汽车动力电池全生命周期的荷电状态估算方法[J]. 电工技术学报, 2020, 35(4): 698-707.

Liu Fang, Ma Jie, Su Weixing, et al. State of charge estimation method of electric vehicle power battery life cycle based on auto regression extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 698-707.

[5] Ramadan H S, Becherif M, Claude F. Extended Kalman filter for accurate state of charge estimation of lithium-based batteries: a comparative analysis[J]. International Journal of Hydrogen Energy, 2017, 42(48): 29033-29046.

[6] 郝文美, 张立伟, 彭博, 等. 动车组钛酸锂电池荷电状态估计[J]. 电工技术学报, 2021, 36(增刊1): 362-371.

Hao Wenmei, Zhang Liwei, Peng Bo, et al. State of charge estimation of lithium titanate battery for electric multiple units[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 362-371.

[7] 裴磊. 基于平衡电压的电动汽车锂离子电池状态估计方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2016.

[8] 宫明辉, 乌江, 焦朝勇. 基于模糊自适应扩展卡尔曼滤波器的锂电池SOC估算方法[J]. 电工技术学报, 2020, 35(18): 3972-3978.

Gong Minghui, Wu Jiang, Jiao Chaoyong. SOC estimation method of lithium battery based on fuzzy adaptive extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3972-3978.

[9] 李超然, 肖飞, 樊亚翔, 等. 基于门控循环单元神经网络和Huber-M估计鲁棒卡尔曼滤波融合方法的锂离子电池荷电状态估算方法[J]. 电工技术学报, 2020, 35(9): 2051-2062.

Li Chaoran, Xiao Fei, Fan Yaxiang, et al. A hybrid approach to lithium-ion battery SOC estimation based on recurrent neural network with gated recurrent unit and Huber-M robust Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 2051-2062.

[10] 庞辉, 郭龙, 武龙星, 等. 考虑环境温度影响的锂离子电池改进双极化模型及其荷电状态估算[J]. 电工技术学报, 2021, 36(10): 2178-2189.

Pang Hui, Guo Long, Wu Longxing, et al. An improved dual polarization model of Li-ion battery and its state of charge estimation considering ambient temperature[J]. Transactions of China Electrotechnical Society, 2021, 36(10): 2178-2189.

[11] Love C T, Virji M B V, Rocheleau R E, et al. State-of-health monitoring of 18650 4S packs with a single-point impedance diagnostic[J]. Journal of Power Sources, 2014, 266: 512-519.

[12] 骆凡, 黄海宏, 王海欣. 基于电化学阻抗谱的退役动力电池荷电状态和健康状态快速预测[J]. 仪器仪表学报, 2021, 42(9): 172-180.

Luo Fan, Huang Haihong, Wang Haixin. Rapid prediction of the state of charge and state of health of decommissioned power batteries based on electrochemical impedance spectroscopy[J]. Chinese Journal of Scientific Instrument, 2021, 42(9): 172-180.

[13] Galeotti M, Cinà L, Giammanco C, et al. Performance analysis and SOH (state of health) evaluation of lithium polymer batteries through electrochemical impedance spectroscopy[J]. Energy, 2015, 89: 678-686.

[14] Guo Peiyao, Cheng Ze, Yang Lei. A data-driven remaining capacity estimation approach for lithium-ion batteries based on charging health feature extraction[J]. Journal of Power Sources, 2019, 412: 442-450.

[15] Tian Jinpeng, Xiong Rui, Shen Weixiang. State-of-health estimation based on differential temperature for lithium ion batteries[J]. IEEE Transactions on Power Electronics, 2020, 35(10): 10363-10373.

[16] 杨胜杰, 罗冰洋, 王菁, 等. 基于容量增量曲线峰值区间特征参数的锂离子电池健康状态估算[J]. 电工技术学报, 2021, 36(11): 2277-2287.

Yang Shengjie, Luo Bingyang, Wang Jing, et al. State of health estimation for lithium-ion batteries based on peak region feature parameters of incremental capacity curve[J]. Transactions of China Electrotechnical Society, 2021, 36(11): 2277-2287.

[17] 李超然, 肖飞, 樊亚翔, 等. 基于卷积神经网络的锂离子电池SOH估算[J]. 电工技术学报, 2020, 35(19): 4106-4119.

Li Chaoran, Xiao Fei, Fan Yaxiang, et al. An approach to lithium-ion battery SOH estimation based on convolutional neural network[J]. Transactions of China Electrotechnical Society, 2020, 35(19): 4106-4119.

[18] Han Xuebing, Ouyang Minggao, Lu Languang, et al. Simplification of physics-based electrochemical model for lithium ion battery on electric vehicle. Part II: Pseudo-two-dimensional model simplification and state of charge estimation[J]. Journal of Power Sources, 2015, 278: 814-825.

[19] 王萍, 弓清瑞, 张吉昂, 等. 一种基于数据驱动与经验模型组合的锂电池在线健康状态预测方法[J]. 电工技术学报, 2021, 36(24): 5201-5212.

Wang Ping, Gong Qingrui, Zhang Jiang, et al. An online state of health prediction method for lithium batteries based on combination of data-driven and empirical model[J]. Transactions of China Electrotechnical Society, 2021, 36(24): 5201-5212.

[20] 董明, 范文杰, 刘王泽宇, 等. 基于特征频率阻抗的锂离子电池健康状态评估[J]. 中国电机工程学报, 2022, 42(24): 9094-9105.

Dong Ming, Fan Wenjie, Liu Wangzeyu, et al. Health assessment of lithium-ion batteries based on characteristic frequency impedance[J]. Proceedings of the CSEE, 2022, 42(24): 9094-9105.

[21] 颜湘武, 邓浩然, 郭琪, 等. 基于自适应无迹卡尔曼滤波的动力电池健康状态检测及梯次利用研究[J]. 电工技术学报, 2019, 34(18): 3937-3948.

Yan Xiangwu, Deng Haoran, Guo Qi, et al. Study on the state of health detection of power batteries based on adaptive unscented Kalman filters and the battery echelon utilization[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3937-3948.

[22] Chaoui H, Ibe-Ekeocha C C. State of charge and state of health estimation for lithium batteries using recurrent neural networks[J]. IEEE Transactions on Vehicular Technology, 2017, 66(10): 8773-8783.

[23] Wei Zhongbao, Zhao Jiyun, Ji Dongxu, et al. A multi-timescale estimator for battery state of charge and capacity dual estimation based on an online identified model[J]. Applied Energy, 2017, 204: 1264-1274.

[24] 李超然, 肖飞, 樊亚翔, 等. 基于深度学习的锂离子电池SOC和SOH联合估算[J]. 中国电机工程学报, 2021, 41(2): 681-692.

Li Chaoran, Xiao Fei, Fan Yaxiang, et al. Joint estimation of the state of charge and the state of health based on deep learning for lithium-ion batteries[J]. Proceedings of the CSEE, 2021, 41(2): 681-692.

[25] Gomez J, Nelson R, Kalu E E, et al. Equivalent circuit model parameters of a high-power Li-ion battery: thermal and state of charge effects[J]. Journal of Power Sources, 2011, 196(10): 4826-4831.

[26] Zou Changfu, Zhang Lei, Hu Xiaosong, et al. A review of fractional-order techniques applied to lithium-ion batteries, lead-acid batteries, and supercapacitors[J]. Journal of Power Sources, 2018, 390: 286-296.

[27] 齐乃明, 秦昌茂, 王威. 分数阶系统的最优Oustaloup数字实现算法[J]. 控制与决策, 2010, 25(10): 1598-1600.

Qi Naiming, Qin Changmao, Wang Wei. Optimal Oustaloup digital realization of fractional order systems[J]. Control and Decision, 2010, 25(10): 1598-1600.

[28] Xue Jiankai, Shen Bo. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34.

Joint Estimation of the SOC-SOH Based on Lithium Battery Model and Fractional Order Theory

Zhao Jingying1Hu Jin1Zhang Xuehui1Zhang Wenyu2

（1. State Key Laboratory for Reliability and Intelligence of Electrical Equipment Hebei University of Technology Tianjin 300130 China 2. State Grid Hebei Zhangjiakou Scenery Storage and Transportation New Energy Co. Ltd Zhangjiakou 075000 China）

Traditional state of charge (SOC) estimation algorithm of lithium battery is often based on equivalent circuit model, which has low accuracy and too many parameters. And the application of equivalent circuit model in state of health (SOH) estimation is limited because of the disadvantages. In addition, the capacity attenuation of lithium battery is often ignored to result in poor timeliness of SOC estimation. There is a coupling relationship between SOC and SOH of lithium battery. SOC-SOH joint estimation is an effective means during life cycle, but joint estimation model is relatively complex and imperfect, which doesn’t support the estimation requirements. This paper presented a joint SOC-SOH estimation model with equivalent circuit model and fractional order theory. By adaptive extended Kalman filter (AEKF) algorithm and capacity parameter modification method, the accuracy and the timeliness of the state estimation were improved.

Firstly, based on the second order RC model of lithium battery, the state equation was established. Considering the time-varying characteristics of noise covariance, dynamic noise covariance parameter was obtained by calculating the cumulative error, and AEKF algorithm was proposed to estimate the SOC of lithium battery. Secondly, aiming at the of excessive parameters in integer order model, the RC series module was simplified by fractional calculus theory to acquire a fractional order model with high precision and few parameters. The parameters were identified by fuzzy controller. Based on the charging conditions and the polarization characteristics of lithium battery, the interval constant current charging time and the fractional-order model parameters were determined as health factors. Thirdly，by use of SSA to optimize BP neural network for the global optimal solution of the weight, nonlinear relationship between health factors and SOH was analyzed to design SOH estimation model. Finally，considering the capacity attenuation of lithium battery and the measurement accuracy of health factors, SOH estimation value was used to modify the capacity parameters and SOC estimation value was used to determine the initial sampling point of health factor to develop a SOC-SOH joint estimation model.

Aging tests, dynamic condition tests of US06 and DST of lithium battery are designed to verify the joint SOC-SOH estimation model. In dynamic tests of US06 and DST, the results show that maximum error of SOC estimation accuracy based on AEKF algorithm and EKF algorithm is less than 1% and more than 3% respectively, which verified the effectiveness of SOC estimation model with AEKF algorithm. In aging tests, the effectiveness of health factors was verified and the influence of accuracy between SOC and SOH estimates was analyzed. The results show that the correlation coefficient between interval constant current charging time and SOH is greater than 0.96, the correlation coefficient between fractional order model parameters and SOH is greater than 0.95, which expressed the strong correlation of the health factors. The maximum errors of SOH estimation based on health factors acquired by AEKF and EKF were less than 1% and more than 2%, respectively, which showed the SOH estimation improvement with health factors acquired by AEKF. By capacity parameter modification, the maximum error of SOC estimation could decrease at less than 1%, while the maximum error of SOC estimation is more than 22% without modification. Meanwhile, with different capacity modification accuracies, the maximum errors of SOC estimation could be ensured to be less than 1.5%, which reduced the estimation errors and improved the timelines with the joint SOC-SOH estimation model.

The following conclusions can be drawn from the analysis: (1) Compared with EKF, the actual dynamic noise covariance is considered in AEKF algorithm proposed. It is more appropriate to establish SOC model to effectively improve SOC estimation accuracy. (2) Fractional order model can better reflect the polarization characteristics of lithium battery. With the health factors extracted based on charging conditions and fractional order model parameters, SOH estimation model established can reduce the estimation error. (3) AEKF algorithm is used to adaptively monitor the charging and discharging state of lithium battery to acquire accurate health factors. SOH estimation value is used to modify capacity parameters instead of fixed capacity parameters because of actual capacity attenuation. The joint estimation model designed is more suitable for the actual change. It has stronger timeliness and robustness.

Lithium battery, fractional order model, health factor, state of charge, state of health

TM912

10.19595/j.cnki.1000-6753.tces.221092

国家自然科学基金项目（51077097）和天津市科技支撑计划重点项目（10ZCKFGX02800）资助。

2022-06-10

2023-02-01

赵靖英 女，1974年生，教授，硕士生导师，研究方向为电工装备可靠性理论及应用。E-mail：zhao_team@163.com（通信作者）

胡 劲 男，1997年生，硕士研究生，研究方向为电工装备可靠性理论及应用。E-mail：Hjin_hebut@163.com

（编辑 李冰）