基于虚拟探照灯的离合制动履带底盘寻径跟踪

陈子文，熊扬凡，胡宗锐，李聪，庞有伦，杨明金※

（1. 西南大学工程技术学院，重庆 400715；2. 重庆工业职业技术学院机械工程与自动化学院，重庆 401120；3. 重庆市农业科学院农业机械化研究所，重庆 401329）

0 引言

农业机械自动导航是精准农业的关键技术，可以极大减轻操作人员的劳动强度，同时提高作业质量与作业效率[1-3]。底盘总成是移动式农用动力机械的核心部件之一，在通用式底盘上搭载其他功能性农具可实现多种农业生产作业[4]。相较于普通轮式拖拉机，自走式履带底盘体积小巧，拥有更低的接地比压、滑转率和滚动阻力系数，地形适应能力广 。尤其在复杂多变的山地和黏湿土壤的田间环境下，履带式底盘表现出卓越的综合性能[5]。

目前，农机装备自动导航研究主要集中在轮式拖拉机和电驱动力平台，涉及的导航控制方法包括PID 控制[6]、模糊控制[7-8]、预瞄跟踪控制[9]、非线性模型预测控制[10]、基于位姿偏差的转向角线性控制[11-12]、基于运动特性的导航控制[13]以及反步滑动模式控制[14]等。然而，针对低成本、技术成熟，采用转向离合器进行转向的油动机械换挡履带底盘的导航系统研究较少。ZHANG等[15]针对单缸柴油履带车导航提出一种基于虚拟阿克曼转向模型的状态反馈导航控制系统，并设计了基于脉宽调制原理的前向比例控制方法，在果园环境中的平均跟踪误差为5.1 cm，跟踪误差标准差为8.4 cm。丁幼春等[16]针对搭载油菜播种机的履带底盘设计了免疫PID 导航控制器，当行驶速度为0.5 m/s 时，其平均导航偏差为4.2 cm，最大偏差为11.9 cm。刘志杰等[17]针对小型履带拖拉机，通过搭载组合导航系统，并利用神经网络提出了一种虚拟雷达模型的路径跟踪控制算法，当行驶速度为0.36、0.75 m/s 时，平均横向偏差分别为3.1、5.1 cm。吴才聪等[18]针对履带底盘提出模糊自适应纯追踪控制方法，水泥路面试验表明，当行驶速度为0.8 m/s 时，模糊自适应纯追踪控制器最大跟踪偏差为3.9 cm，平均绝对偏差为1.8 cm。

在农业作业场景中，应用于此类农用动力机械的路径跟踪算法必须满足较高的精度要求。例如，在播种、施肥和喷药等环节，精准的路径跟踪有助于减少重复覆盖和遗漏区域，从而提高作业效率[19]。同时，较高的行驶速度也可缩减作业周期，以适应农业生产的季节性要求[20]。但过高的速度会导致导航系统的精度和稳定性降低，因此要求跟踪算法在保证导航精度的要求下尽可能提高行驶速度。另一方面，在实际农业作业中，自动导航系统需在较短时间内上线并开始跟踪期望路径。若上线距离过长，不但会降低作业效率，甚至影响整个农业生产过程。然而，油动换挡履带底盘难以进行精准的速度控制，其速度控制只能通过调整油门和机械档位实现，速度滞后较严重，同时由于各侧履带无法单独速度控制，因此只能进行单一模式转向。值得关注的是，在离合制动式履带平台上，每一次的转向动作，尤其在直线跟踪过程中，都会对车辆造成一次刚性冲击。这主要是由于转向时，履带平台的单侧履带轮锁死，从而导致平台速度瞬间改变造成的。频繁转向会导致搭载在平台上的功能性农具的作业精度下降，甚至无法正常工作；并且过于频繁的纠偏可能会对农具或履带平台自身造成损坏。故此类履带平台在农业作业中并不适宜频繁转向纠偏。目前的各类路径跟踪算法并未充分考虑车辆在跟踪过程中的纠偏次数，尤其是针对离合制动式履带平台的算法，因此，在设计适用于此类平台的跟踪算法时，既需要严格限制纠偏次数，又要确保跟踪精度得到满足。这一原则有助于提高农业作业效率，减少搭载农具的精度损失和避免农具及履带平台的损坏。

本文以3WZF-400 汽油驱动履带底盘为研究对象，提出一种虚拟探照灯寻径路径跟踪方法，通过仿真和导航试验对系统和算法性能进行验证，该方法综合考虑离合制动式履带平台在跟踪过程中的纠偏次数限制和跟踪精度需求，旨在为此类平台提供一种高效、稳定的导航解决方案。

1 材料与方法

1.1 离合制动式履带底盘构成

本文以3WZF-400 汽油驱动履带底盘（苏州博田自动化技术有限公司生产）为研究对象搭建自动导航系统，如图1 所示，主要由履带总成、传动系统和操纵系统组成。履带车总长1.2 m，宽0.9 m，橡胶履带宽0.2 m，动力由5.4 kW 单缸汽油机提供，该履带底盘体积小，对各种果园、田地道路条件有较强适应性。

图1 离合制动式履带底盘系统组成Fig.1 Composition of clutch-brake track chassis

履带底盘动力传动与转向系统如图2 所示。发动机将动力传递给手动换挡变速箱，离合器手柄可控制动力离合器的闭合，将动力传递给驱动桥，左右两个驱动轮前端均设有常闭离合器，通过转向手闸轧线控制离合器打开，切断动力传输，实现停机或转向。由于该类动力平台通过控制离合器闭合，实现车辆制动或转向，故将此类结构和操控方式称为离合制动式履带底盘。为实现履带底盘自动操控，对手动操控系统进行升级，采用气动系统代替手动操作，应用3 组独立控制的双作用气缸拉动轧线控制3个离合器的闭合，实现启停、直线行驶、转向等动作[21]。

图2 履带底盘转向结构示意图Fig.2 Steering mechanism diagram of track chassis

1.2 导航控制系统架构

导航控制系统采用以ARM Cortex M4 为内核的STM30F303 VCT6 单片机作为中控器，数据接收、数据解析、运算处理等任务均由该单片机完成。全球卫星导航系统（global navigation satellite system，GNSS）采用上海华测导航技术股份有限公司的P3-DU 北斗高精度定位测向接收机，搭配有载波相位差分技术（real-time kinematic，RTK），多系统双频，支持双天线定位测向解算，在装备有移动站接收机的基础上，通过搭建基站接收机和无线电台，实现RTK-GNSS 高精度定位数据的接收。导航控制系统整体架构如图3 所示，RTK-GNSS定位模块利用无线电台接收差分信号，经差分系统校准后，中控器采取通用异步串行通信（universal asynchronous receiver/transmitter，UART）方式获取高精度定位数据。将解析数据与设定的期望路径进行比较，利用偏差跟踪算法得到预期驾驶动作，通过控制执行机构以达到路径跟踪的目的。上位机可以监控导航控制系统的工作状态，其与中控器之间采用UART 方式并通过ZigBee 无线模块进行数据的相互传输。中控器将解析后的定位信息以及导航过程中所产生的各项导航参数反馈给上位机，在系统发生异常时可通过发送相关指令终止导航作业。在本研究中，选择ZigBee 模块主要考虑到其成本低、体积小、使用方便等优势，有利于在短时间内实现系统原型的搭建与初步测试。

图3 导航控制系统架构Fig.3 Structure of navigation control system

2 路径跟踪控制方法

2.1 履带底盘运动学模型

根据离合制动式履带底盘的工作原理，只能依靠单侧履带轮完全制动来实现转向，即转向时内侧履带的驱动轮角速度为零，外侧履带轮角速度不变，且履带底盘作业过程中驱动轮的速度无法随意调节，在导航平面坐标系X-O-Y（n系）中建立履带车运动学模型，如图4 所示，G(x,y)为履带车几何中心坐标。考虑到农业作业中一般行驶速度较低，可做如下假设：1）履带底盘质心与几何中心重合；2）履带底盘在作业过程中非制动时履带的带速恒定；3）忽略双侧履带的滑移和滑转 。

图4 离合制动式履带底盘运动学模型Fig.4 Kinematic model of clutch-brake track chassis

定义履带底盘的航向角ψ为Y轴正方向顺时针旋转至速度v的角度，转向角φ的大小与转向对应的圆心角相等，其值与转向持续时间有关。根据运动学原理有：

式中rl表示左侧履带几何中心相对于旋转中心o的距离，m。由于右转时右侧履带完全制动，即：

将式（5）带入式（3）可得：

由式（6）可看出，履带底盘的旋转中心位于履带的几何中心处，车辆进行转向时，旋转中心在左右两侧履带的几何中心之间切换，故两侧履带可独立控制转速和转向的差速模型不适用于此类履带底盘。

2.2 虚拟探照灯寻径跟踪算法原理

路径跟踪的实质是通过控制车辆的运动减少车辆与期望路径之间的偏差，在农机导航作业中，作业路径通常由直线段构成。为提高作业质量和效率，要求农机自动导航系统上线快速稳定、直线跟踪精度高以及对颠簸复杂路面抗干扰性好[22]。目前大多数跟踪算法按照某种控制策略计算车辆的前轮期望转角，从而通过改变前轮转角控制车辆运动轨迹的曲率，如纯跟踪算法[23]、Stanley 算法[24]、MPC 算法[25-26]。对于差速转向的履带底盘，可以通过改变双侧履带的速度调整履带底盘运动轨迹的曲率，所以可利用转换轮式车辆的跟踪算法实现对目标路径的跟踪控制。而对于离合制动式履带底盘，双侧履带的带速不可随意调节，同时受到速度传感器缺失和路面环境等因素影响，利用转向时间间接获取期望转向角会产生较大误差。此外，为避免履带底盘在跟踪过程中频繁转向纠偏导致的作业精度下降、农具以及履带底盘自身损坏，应对纠偏次数严格限定。

本文提出的虚拟探照灯寻径跟踪（virtual searchlight pathfinding tracking，VSPT）算法假设履带底盘搭载一种光线射程为无限远的虚拟探照灯，并设定一个位于期望路径及其延长线上且不断运动的假想目标点C，通过模拟探照灯搜索物体的方式建立履带底盘不断追逐目标点的路径跟踪方法。假定该虚拟探照灯安装于履带底盘几何中心处，其视域角为γ，且光束投射方向与履带底盘航向一致。图5 所示，若目标点C位于虚拟探照灯视域内，则履带底盘直线前进，反之，目标点C位于虚拟探照灯视域范围外，履带底盘通过转向寻找该目标点并使其位于视域内。

图5 基于虚拟探照灯的履带底盘转向示意图Fig.5 Track chassis steering diagram based on virtual searchlight

设履带底盘导航路径坐标点序列A1，A2，···，Ai，···，An，如 图6 所示，以AiAi+1为期望路径进行分析，视域角的大小影响导航作业的稳定性，当履带底盘逐渐靠近期望路径时，视域角γ不变，由于视场变小，则视域内可见的期望路径变短，类比于真实场景中驾驶员视野变窄，此时算法对横向偏差极度敏感，将不断调整航向导致系统振荡。同时在横向偏差较小的情况下，若视域角γ过大，也会导致导航误差增加，系统稳定性下降。故本文提出一种基于横向偏差指数的视域角动态变化方法，视域角反比于横向偏差d的λ次方，指数λ可用于调节视域角的变化速率，具体计算式为

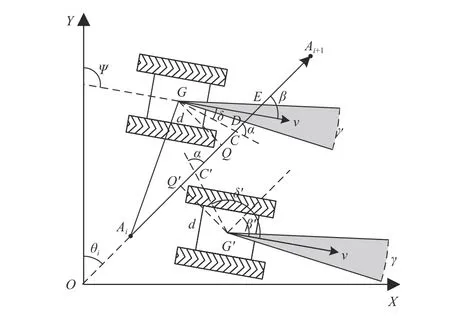
图6 路径跟踪模型Fig.6 Path tracking model

式中k1表示视域增益，rad·m；d表示横向偏差，m；λ表示横向偏差指数。

规定目标点始终于车辆前方，即位于直线QAi+1及履带底盘几何中心G在期望路径AiAi+1上的投影点Q向Ai+1点方向的延长线上。目标点C的位置控制履带底盘向期望路径靠近的迫切程度。低速行驶时履带底盘目标点靠近当前位置，履带底盘应尽快接近期望路径，高速行驶时则应避免很小的横向偏差引起跟踪振荡。因此将直线QC的长度m与履带底盘行驶速度之间设置为正比例关系，计算式为

式中k2表示目标增益，s-1。

若直接利用点C坐标与视域方程判断目标点C是否位于视域范围内，则运算过程较为复杂繁琐。为简化计算过程，本文采用期望航向偏差角α作为中间参数进行求解，α可表示为

由式（9）可知，α与横向偏差有关，d愈大，α愈趋近于0.5π，反之，α趋近于0。

如图6 所示，若位于G点与G'点时履带底盘参数ψ，θi，α，d等相等，则β绝对值相等。而G点位于有向线段AiAi+1左侧，G'点位于右侧，显然绝对值相等的β不能够准确描述上述情况。为赋予β更多物理含义，定义直线DE的长度为履带平台的视野范围，若视野范围大于0，则航向偏差角β为正值，反之，航向偏差角β为负值。

履带底盘航向与假想目标点之间的夹角δ可直接指导履带底盘的驾驶动作，根据α和β的取值，可通过VSPT 算法进行求解。为保证履带底盘通过转向搜寻目标点时路径最短，即转角最小，δ绝对值应小于π，且转弯方向总是朝着δ绝对值逐渐减小的方向。若δ为正，目标点C位于履带底盘右侧，需向右转向；若δ为负，则目标点C位于履带底盘左侧，向左转向。

2.3 基于数据流图的软件设计及算法实现

数据流图（data flow diagram，DFD）是描述系统信息流以及数据变换流程的图形[27]，具有描述系统逻辑结构的能力[28]。建立的DFD 如图7 所示，数据源包括上位机、RTK-GNSS 定位系统以及空闲中断服务函数。上位机提供用户预设的基于WGS84 坐标系（e系）下的期望路径坐标序列和原点坐标，系统将两者做坐标转换[26]，得到n系下的期望路径坐标。RTK-GNSS 定位系统通过标准串口实时输出不定长数据。为解决不定长数据稳定接收同时提高系统工作效率，采用直接存储器访问（direct memory access，DMA）方式，结合串口空闲中断和循环队列策略进行数据接收，通过数据解析以及坐标转换得到履带底盘航向、速度以及n系下的定位坐标。将数据传入VSPT 算法后解算出行驶动作并传递给执行机构，从而完成履带底盘的自动驾驶。

图7 数据流图Fig.7 Data flow diagram

通过DMA 传输，结合空闲中断与循环队列的数据接收方式的优势在于系统进行工作运算的同时能够进行数据的接收。每次进行数据提取时均能捕捉到最新序列的数据帧，提高了定位数据与实际位置的吻合度；省略了CPU 数据接收流程，提高了系统运算的效率和稳定性。

3 仿真与现场试验

3.1 评价指标

为精确评价路径跟踪算法的导航效果，将履带底盘跟踪期望路径的过程以上线点为界限分为上线过程以及直线跟踪过程，如图8 所示。起始点作为履带底盘的初始位置，上线点指横向偏差小于3.0 cm 同时航向偏差小于2.0°且与起始点相距最近的采样点。上线过程采用上线距离作为评价指标；直线跟踪过程采用横向偏差、航向偏差均值、标准差和均方根以及纠偏次数作为评价指标。

图8 上线过程与直线跟踪过程Fig.8 On-line process and straight-line tracking process

上线距离为从起始点到上线点的实际轨迹在期望路径上的投影长度，表征系统在偏离期望路径时的响应速度。

在国外，19世纪40～60年代，牛津大学使用“推广”一词指大学的推广活动，即建议；而到19世纪70年代，剑桥大学将校外开展的教育活动称之为“推广教育”。在本世纪初，美国建立了赠地学院和合作推广机构，开始真正使用“农业推广”这一表述。1915年，美国《史密斯—来弗联邦推广法》颁布实施，使得农业推广法律化，同时也给“农业推广”赋予新的意义。

横向偏差均值ldm为直线跟踪过程中履带平台几何中心位置采样点距期望路径横向偏差d绝对值的均值，可表示为

式中下标j表示采样点序号；q表示采样点总数；(xj,yj)表示履带底盘在平面坐标系下的几何中心坐标，m；Ai(Xi,Yi)，Ai+1(Xi+1,Yi+1)表示期望路径两端点在平面坐标系下的坐标，m。

航向偏差均值cdm为直线跟踪过程中履带平台航向角ψ与θi偏差绝对值的平均值，可表示为

纠偏次数指上线后导航系统自动控制履带底盘左、右转向的次数，衡量算法对直线跟踪的振荡情况。履带底盘在直线跟踪中频繁左、右转向会导致车体剧烈振动，从而影响定位精度，延长导航时间，无法满足作业平稳性的需求；同时车体频繁振荡对机械、电机结构的耐久性均产生影响。试验中动态采集履带底盘转向控制信号并传输给上位机，采样频率5 Hz。如图9，单次试验过程中采集150个控制信号，图中数据点代表控制器发出的右转、左转或直行控制信号。图中虚线为上线时刻所对应的控制数据序列的位置，纠偏次数为上线之后的转向次数。由于履带平台转向控制响应具有滞后性，经试验验证，单帧控制数据无法使履带平台转向，判定为控制噪声，3 帧及以上可作为判断转向的依据。因而定义一次纠偏为上位机接收连续3 帧及以上的转向数据。试验中150个控制数据点中发生了3 次纠偏。

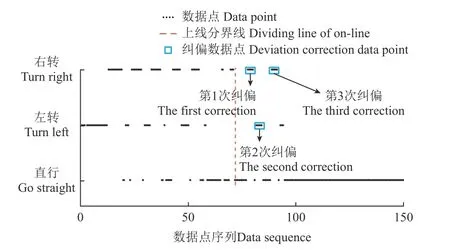
图9 纠偏次数统计Fig.9 Statistical of deviation correction

3.2 仿真试验

为验证虚拟探照灯寻径跟踪算法的导航效果并对指数λ、视域增益k1、目标增益k2进行标定，利用MATLAB对其进行仿真试验。设定仿真过程中的路径起始点坐标为(0,0)，终点坐标为(10 m,10 m)，履带底盘的初始横向偏差为0.5 m，初始航向偏差角β为25°，采样时间为0.2 s，假设双侧履带在非制动情况时速度恒定，为0.4 m/s，履带轴线间距b=0.9 m。取初始k1=0.005 rad·m，k2=6.0 s-1进行仿真试验，试验结果如表1。通过对比导航效果（试验号1～5），选取较优值λ=1/4。

表1 路径跟踪仿真试验结果Table 1 Path-tracking simulation test results

仿真试验发现，控制参数k1、k2的取值对导航效果有重要影响。因此在λ取值确定后，需初步评估k1、k2的合理值，为现场试验提供依据。图10 为上线过程和直线行驶过程的仿真轨迹。根据图10 和表1 可知，视域增益k1对上线距离影响较小，但对直线跟踪过程中ldm的大小有重要影响，在合理范围内视域增益k1增大则ldm变小。目标增益k2对上线距离有重要影响，随着k2的增大，上线距离先减小后增大，这是由于过大的k2会引起较大的超调，降低履带底盘的上线性能，且k2越小轨迹越平滑，反之愈发激进。仿真结果表明：虚拟探照灯寻径的跟踪算法具有较高的跟踪精度，能够满足导航要求。通过比较导航效果，最终选取λ的较优值为1/4，k1的较优值为0.005 rad·m，k2为6.0 s-1。

图10 路径跟踪仿真轨迹Fig.10 Path tracking simulation trajectory

3.3 现场试验

3.3.1 试验方法

本试验旨在探究并优化VSPT 算法对于直线跟踪的性能。试验在西南大学内水泥路和试验田土路开展，试验时间为2022 年12 月8 日至9 日。利用华测高精度RTK-GNSS 系统（数据更新频率为5 Hz）采集试验场地中两点坐标，并将其连线作为期望路径，设置其中一点作为当地水平坐标系下的坐标原点，导航系统运行时控制器将经纬度转换为n系下的坐标，并实时向上位机发送履带底盘的当前坐标、横向偏差、航向偏差等导航参数，以控制履带底盘导航运行。

考虑到作业环境以及作业参数的复杂性，为全面验证本文提出算法的导航效果，首先进行算法参数验证，然后针对不同初始参数、运动参数和路况情况进行对比试验。算法参数验证试验以仿真结果为依据，通过实地试验验证导航效果。初始参数试验通过设置履带平台不同初始位姿，包括初始横向偏差和初始航向偏差，验证导航算法对不同初始状态的导航效果，试验中选取初始横向偏差分别为0.5、1.0 和1.5 m，初始航向偏差角选取±25°。运动参数试验为不同运动速度下的导航试验，旨在验证算法对不同速度的适应性，并分析速度对导航效果的影响，选取低速（1 档）、中速（2 档）、高速（3 挡）3 种档位，对应的实测速度分别为0.4、0.8 和1.2 m/s。考虑到履带底盘的应用场景，选择水泥路面和具有杂草覆盖的土路进行路况对比试验。

3.3.2 算法参数可行性验证

利用上文仿真试验所标定的算法参数进行现场实验，水泥路面采用低速1 档，设置初始横向偏差0.5 m 以及初始航向偏差角25°，取控制参数k1=0.005 rad·m、k2=6.0 s-1、λ=1/4，该组试验重复5 次，结果取均值，结果见表2 中试验号1。

表2 现场试验结果Table 2 Field test result

较仿真结果相比，现场试验各项评价指标均有所增加，上线距离增大0.52 m，横向和航向偏差绝对值均值分别增大0.35 cm 和1.34°。分析其主要原因为仿真运动学模型中未考虑履带底盘的滑移、滑转以及定位系统的噪声等误差，同时执行机构存在滞后现象。根据现场试验结果，仿真获取的控制参数可实现较好的导航效果，实际上线距离为1.44 m，横偏均值为0.41 cm，且航偏均值为1.81°。

3.3.3 初始位姿参数导航试验

该试验探究在不同初始位姿参数下算法的导航效果，试验在水泥路面上进行，以低速1 档速度运动，设置3水平初始横向偏距因素和2 水平航向偏距因素，初始航向偏差±25°，表示初始航向角相比期望路径的航向角偏离25°，±代表航向偏差的方向，+表示车头朝向期望路径，-表示车头背向期望路径，每组试验重复5 次，结果取均值，试验结果见表2 中试验序号1～6。

试验结果表明，在不同初始位姿下VSPT 算法均能达到较好的导航精度，平均上线距离为1.64 m，直线跟踪过程中横向偏差绝对值的平均值、标准差和均方根的平均值分别为0.44、0.31 和0.56 cm，航向偏差绝对值的平均值、标准差和均方根分别为1.57°、0.55°和1.58°，平均纠偏次数为3.5 次。在保证导航精度和导航效率的前提下，算法可允许合理范围内的波动。

图11 为不同初始参数导航效果对比，可见，初始横向偏差增大导致上线距离略微增加，初始航偏设置为-25°时，车辆调整航向所需时间更长。如图11a、11b 所示，在不同初始位姿下，横向偏差与航向偏差都能被快速消除，在初始横偏为1.5 m 的情况下，上线距离小于2 m。由图11c、11 d 可看出，履带平台的上线过程中，无超调量，振荡较小。履带底盘在上线和直线跟踪过程中轨迹不够平滑主要由履带底盘的运动特性导致，离合制动式履带平台无法实现平滑转向，履带底盘分两步完成上线，分别是快速接近和矫正过程。

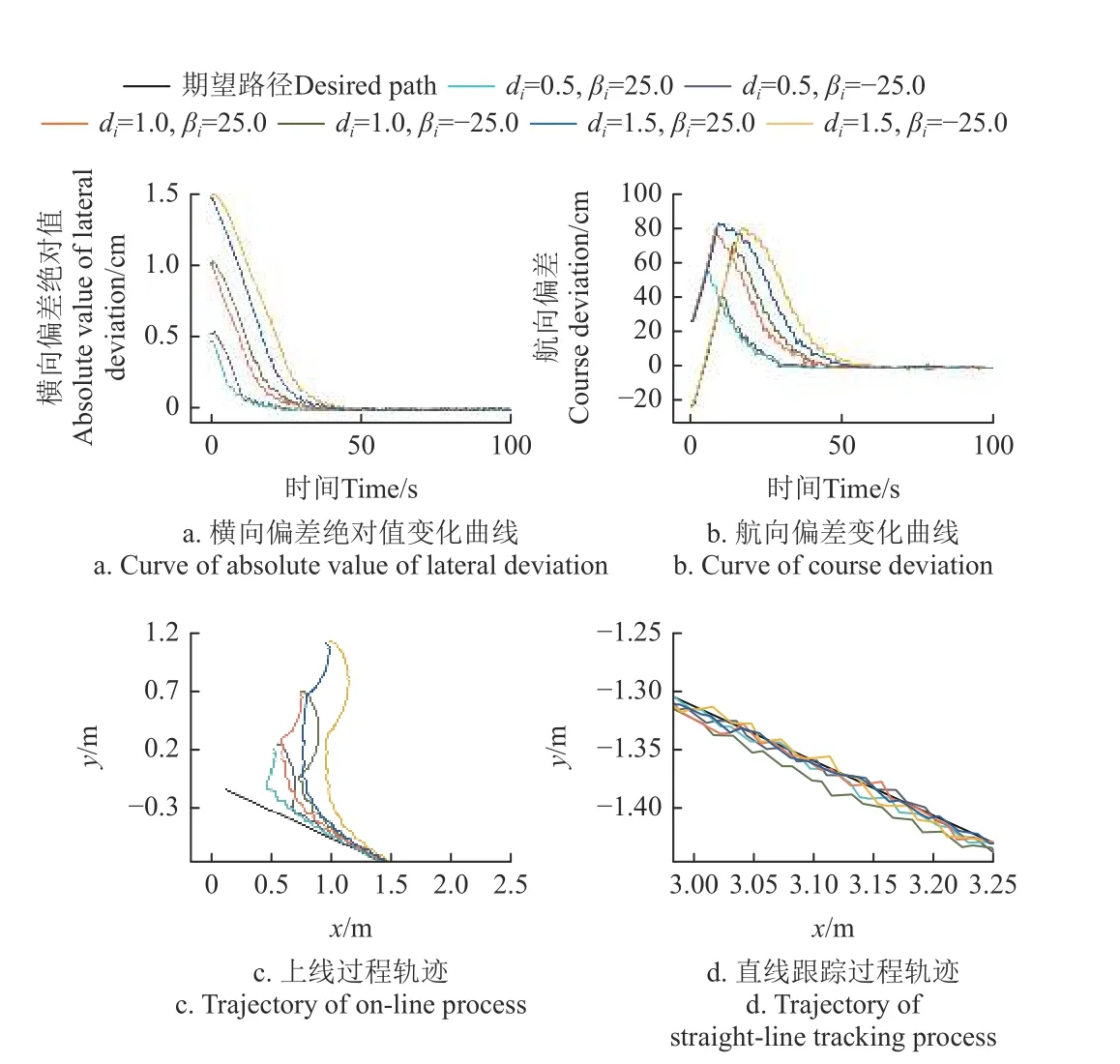
图11 不同初始位姿参数的试验结果Fig.11 Test results of different initial posture parameters

由图11b 可见，航向偏差出现最大值前均属于快速接近过程，之后航向偏差逐渐减少到零点附近，这个过程是航向偏差的矫正过程，故在图11c 中上线过程轨迹会出现折点，后续试验发现，降低目标增益k2，可使折点处更加平滑，但会明显增加上线距离，降低直线跟踪效率。直线跟踪过程波动较小，出现的波动主要由于机器震动所导致差分导航系统信号跳动引起。

3.3.4 运动参数导航试验

为验证该算法在履带底盘不同速度下的导航效果，进行不同档位下3个速度水平的单因素试验，试验中初始横向偏距为0.5 m，初始航向偏差为25°，试验在水泥路面上进行。试验结果见表2 中试验号7～11，以1 号试验作为对照组。1 号和7 号试验除了速度外，其余参数均相同，对比可知，提高速度使上线距离略微减小，但导航精度明显下降，横向偏差和航向偏差均值相比低速分别增大156.10%、11.05%，且纠偏次数增大到23 次。由图12 中可明显看出直线跟踪过程中的振荡情况。此时提高k1降低k2（见表2 中试验号8）可得到处于2 档速度下的较优控制参数k1=0.010 rad·m、k2=6.0 s-1，能有效减小上线后的纠偏次数且能减少跟踪误差，从而提高导航精度。若进一步提高k1降低k2（见表2 试验序号9），将牺牲部分导航精度，进一步降低纠偏次数，以减少系统振荡。可见k2对上线性能有明显影响，提高k2可明显减少上线距离，这与仿真结果一致。在高速3 挡（1.2 m/s）下，取k1=0.015 rad·m、k2=4.0 s-1可获得更好的导航效果。对试验号1、8、11 的试验结果求平均，可得平均上线距离为1.54 m，横向偏差绝对值的均值、标准差和均方根分别为0.73、0.57 和0.97 cm，航向偏差绝对值的均值、标准差和均方根分别为1.47°、0.79°和1.59°，平均纠偏次数为4.7。

图12 运动参数变化试验结果Fig.12 Test results of variation of motion parameter

试验结果表明，随履带底盘的速度提升VSPT 算法导航效果变差，但从整体上看，在不同速度情况下若选取相匹配的较优控制参数，仍有较好的导航精度与稳定性，控制参数k1、k2与履带底盘的运行速度有强相关性。

3.3.5 路况对比试验

为验证VSPT 算法对不同路况的适应能力，选取试验田土路面与水泥路面进行对比试验，试验现场如图13所示，试验结果如表2 中试验号12～15。

图13 现场试验路况Fig.13 Road condition of field test

试验中初始航向偏差为25°，初始横向偏距为0.5 m，λ=1/4，速度为0.4 m/s 时，选用仿真所得较优值k1=0.005 rad·m、k2=6.0 s-1。水泥路面试验以试验号1、8、11 为代表，控制初始位姿不变，保证速度挡位、k1以及k2各水平对应，以表2 中试验号12、14、15 的数据进行对比（平均上线距离为1.85 m，横向偏差绝对值的均值、标准差和均方根分别为0.82、0.57 偏差绝对值的均值、标准差和0.98 cm，航向偏差绝对值的均值、标准差和均方根分别为1.35°、0.86°和1.55°，平均纠偏次数为2.7 次），土路面导航结果与水泥路面相似，在0.8 m/s速度下，k1和k2的较优值为0.010 rad·m、k2=5.0 s-1，此时可获得较好的导航效果。因此，算法参数的取值不受到路况的影响，仅与运行速度有关。2 种路况下，由3种速度下平均导航指标数据可见，土路面相比水泥路面上线距离增大0.31 m，直线跟踪过程中平均横向和航向偏差区别不大，平均纠偏次数减少2 次。主要原因是土路面具有更高的路面附着系数，转向更平稳，较少出现过渡转向情况，故纠偏次数和航向偏差均有所降低。总体来看，VSPT 算法适用土路面的导航工况，具有良好的鲁棒性，能够满足农机导航作业需求。后续将深入探索不同速度感知下，k1和k2自动获取和匹配，为实现最佳导航效果提供便捷的控制算法。

本研究提出的VSPT 路径跟踪算法依据离合制动式履带底盘的运动特性，主要用于直线路径跟踪，该类底盘缺点是无法实现转弯半径可变，优点是转弯半径小，因此更适用于折角或原地掉头的转向方式。VSPT 算法针对直线路径上的目标点进行判定，曲线跟踪需要进行适当修正和参数调整，后续将在阿克曼转向和差速转向底盘上深入开展。

4 结论

1）提出离合制动式履带平台的概念，搭建了基于STM30F303 VCT6 控制器的RTK-GNSS 平台自动导航系统，实现履带平台自动启停、转向控制，以及方位信号获取与动态监测功能。

2）建立履带平台运动学模型，提出虚拟探照灯寻径跟踪算法，引入横向偏差指数λ、视域增益k1，目标增益k2，针对横向偏差和速度变化引起的跟踪振荡问题，提出基于横向偏差指数的视域角动态获取方法和基于速度正比例关系的假想目标点判断方法。MATLAB 仿真中发现当运动速度为0.4 m/s、λ、k1和k2分别为1/4、0.005 rad·m 和6 s-1。

3）针对算法的导航效果进行仿真验证，并对不同初始位置、运动参数和运动场景进行对比试验。以仿真参数作为依据，在0.4 m/s 速度下进行水泥路面导航试验，6 种不同初始位姿下，平均上线距离为1.64 m，平均横向偏差和航向偏差为0.44 cm 和1.57°。不同速度导航试验表明，提高速度会导致导航精度降低，适当增大k1并减小k2值可实现较好的导航效果，水泥路面时，3 种速度下获得平均横向和航向偏差为0.75 cm 和1.05°，平均纠偏次数为4.7 次。土路面和水泥路面导航对比试验表明，由于土路面附着系数增加，转向相对平稳，纠偏次数和航向偏差均有所降低，但相同参数下2 种路况导航效果接近，算法具有良好的适应性。