一种双阵元干涉仪相位差变化率提取方法
2023-09-13张阳,孙倩
张 阳,孙 倩
(南京科瑞达电子装备有限责任公司,南京 211100)
0 引 言
利用无源传感器系统对辐射源进行测量定位是无源侦察系统获取目标信息的重要手段,其中基于相位差变化率的定位算法是一种适用单平台的快速定位方法,利用运动学原理,通过测量相位差的变化率,实现对辐射源的无源定位[1]。文献[2]分析了在双阵元干涉仪无源定位系统中利用相位差变化率测量值进行定位解算的方法,但对实际工程应用中如何准确提取相位差变化率的测量值并未开展研究。本文根据传统相位差变化率提取方法,采用一种周期间预测解模糊的方式,利用周期间的信息计算提取相位差变化率,对提取方法展开原理分析,并仿真比较了本文算法与传统算法的性能。
1 测量模型
假设观测站载机机身上阵元E1、E2组成双阵元干涉仪,如图1所示,基线间距为d,信号波长为λ,由于信号到达干涉仪天线两阵元的时间有先后,导致干涉仪接收到的信号存在相位差[2],即
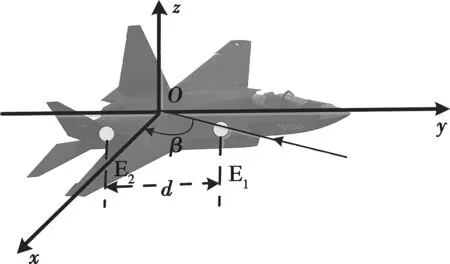
图1 双阵元干涉仪相位差示意图
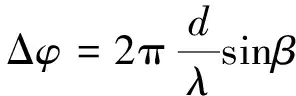
(1)
相位差变化率测距公式为[2]
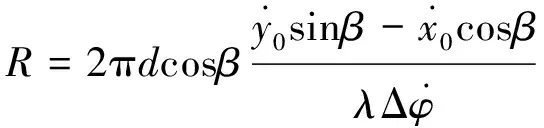
(2)

相位差变化率数据的测量精度越高,定位速度就越快,定位精度就越高[3]。但在工程应用中,阵元E1、E2之间的相位差Δφ是通过接收通道中信号参数测量环节直接测量得到的,测量过程受天线、通道特性以及噪声、温度等影响因素,会引入测量误差,同时测量得到的相位差存在相位模糊。图2为引入工程环境因素影响得到的相位差仿真值,其中目标辐射源信号回访周期为5 s,为满足后续定位需求,须提取出每个回访周期内的相位变化率参数。
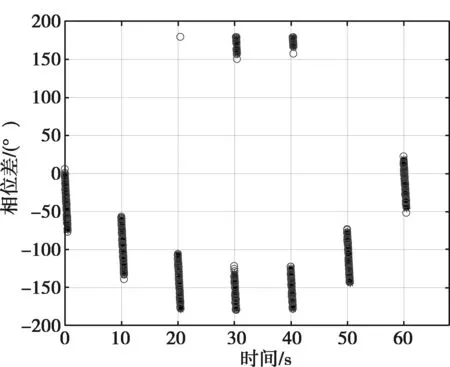
图2 双阵干涉仪相位差样本图
2 传统方法
差分法是一种常用的相位差变化率提取方法[4]。假设目标辐射源回访周期内收到若干个脉冲数据,经测量得到每个脉冲的相位差为Δφi,每个脉冲到达的时间为ti,利用tm与tn这段时间内的相位计算相位差变化率:
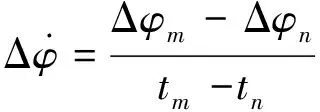
(3)
假设相位差Δφi测量值服从(0,σ)的正态分布,则利用差分法计算得到的相位差变化率误差方差为
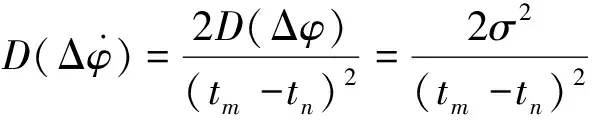
(4)
可以看出,当时间跨度增大时,相位差变化率误差的均方差值减小,因此利用周期内相位差数据计算相位差变化率时,应选取时间跨度大的相位差值。
如图3所示,假设目标辐射源当前回访周期内收到N个脉冲数据,为了增大时间跨度,保证有效的相位差变化率提取精度,选取周期内前后A%的数据参与计算相位变化率:
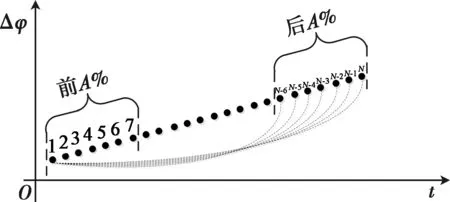
图3 差分方法计算示意图
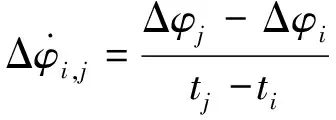
(5)
式中,i=1,2,…,K;j=N-K+1,N-K,…,N,K=N*A%。
通过计算可得到K2个相位差变化率计算值,对这些值求平均,得到该回访周期的相位差变化率提取值:
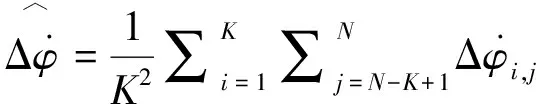
(6)
3 改进方法
传统的差分计算方法最大限度地利用回访周期内的时间跨度,降低了相位差变化率的提取误差,但在工程应用中,当目标辐射源距离较远或面对目标功率管控等手段时,在一个回访周期内定位系统接收机接收到的脉冲数往往极少,导致一个回访周期内可利用的数据时间跨度极小,使相位差变化率提取误差急剧增大,无法满足后续定位需求。本文提出一种利用回访周期间的信息计算相位差变化率的方法,既提升了相位差变化率的提取精度,同时在少量脉冲数据的情况下保证了稳定的相位差变化率精度输出。
由图2样本可知,回访周期间的相位差序列存在模糊,首先对前后两个相邻回访周期间的相位差数据进行解模糊处理。采用前一个周期内差分法-相位差变化率提取得到的相位差变化率估计值,预测下一个周期的模糊数。
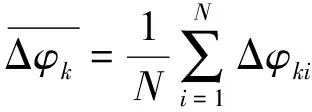
(7)
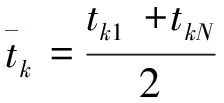
(8)
式中,k=1,2,…为不同回访周期;i=1,2,…为周期内脉冲索引;Δφki为第k个回访周期中第i个脉冲的相位差测量值;tki为第k个回访周期中第i个脉冲的到达时间。
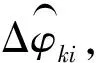
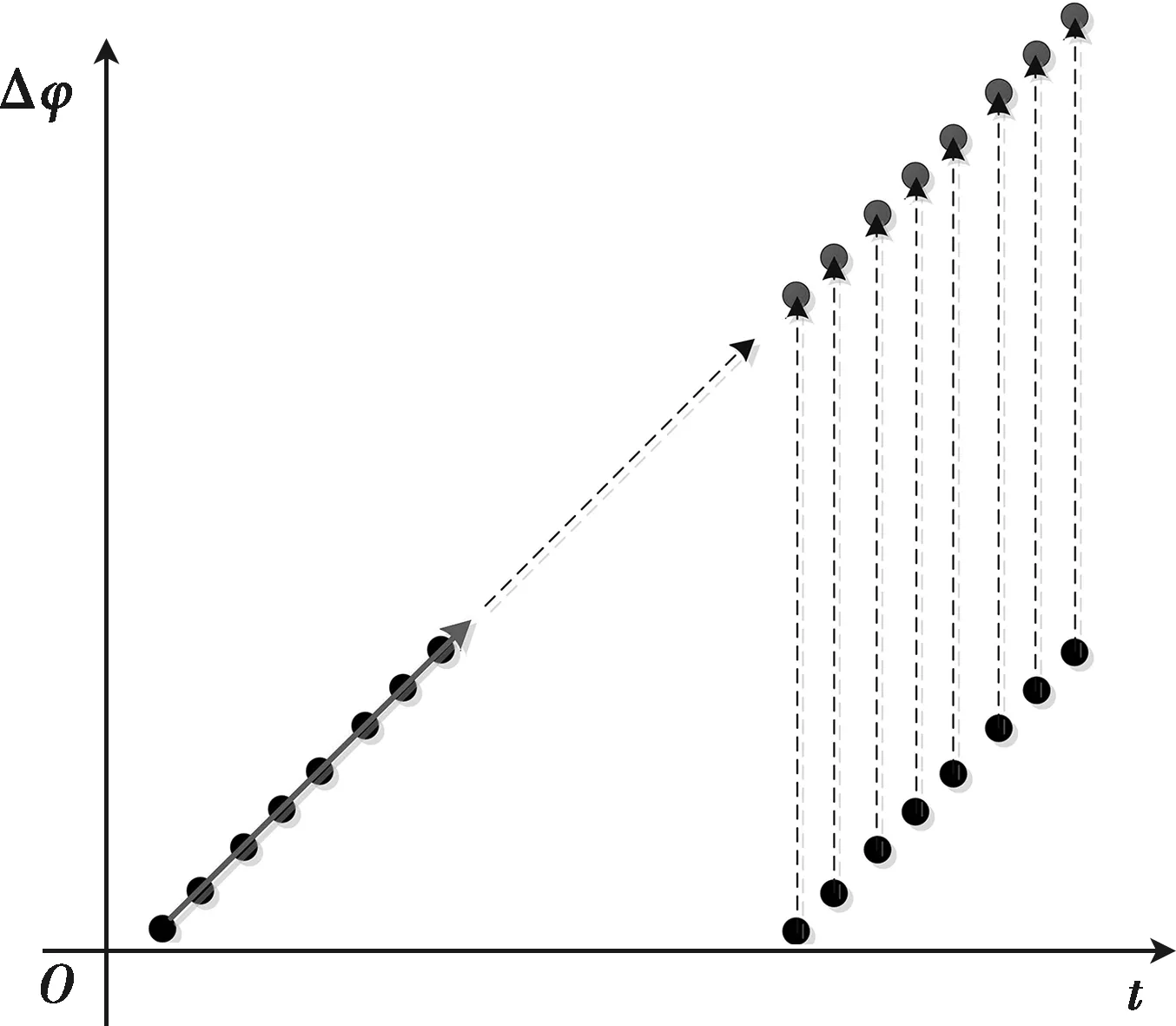
图4 周期相邻解模糊
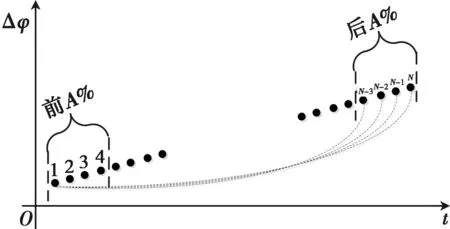
图5 改进方法相位差变化率提取示意图
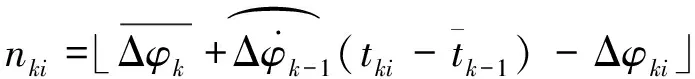
(9)
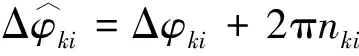
(10)
利用相邻两周期无模糊相位差提取相位差变化率,选取前一周期收到脉冲数的前A%的数据,以及后一周期收到脉冲数的后A%的数据,两者参与相位变化率的计算,如图 5所示。
计算方法如下:
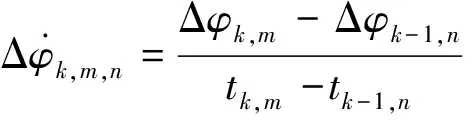
(11)
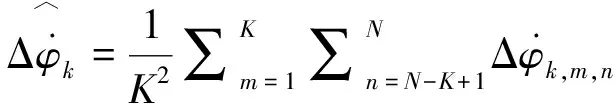
(12)
式中,m=1,2,…,K;n=N-K+1,N-K,…,N;K=N*A%。
利用上述方法,持续对相邻两个周期间进行滑动相位差变化率提取,完成整个处理过程中所有周期的相位差变化率提取。
4 仿真验证
仿真对比上述两种提取方法,建立以平台起点为原点、平台机身方向为Y轴的坐标系,平台飞行速度为200 m/s,飞机平台侦察系统采用双阵干涉仪,基线长度为5 m,相位差测量精度为5°。目标雷达辐射源位置(0,100)km,载频分别为2 GHz、5 GHz、10 GHz,脉冲重复周期为1 ms,雷达扫描周期10 s,相位差变化率提取效果分别如图6~8所示。
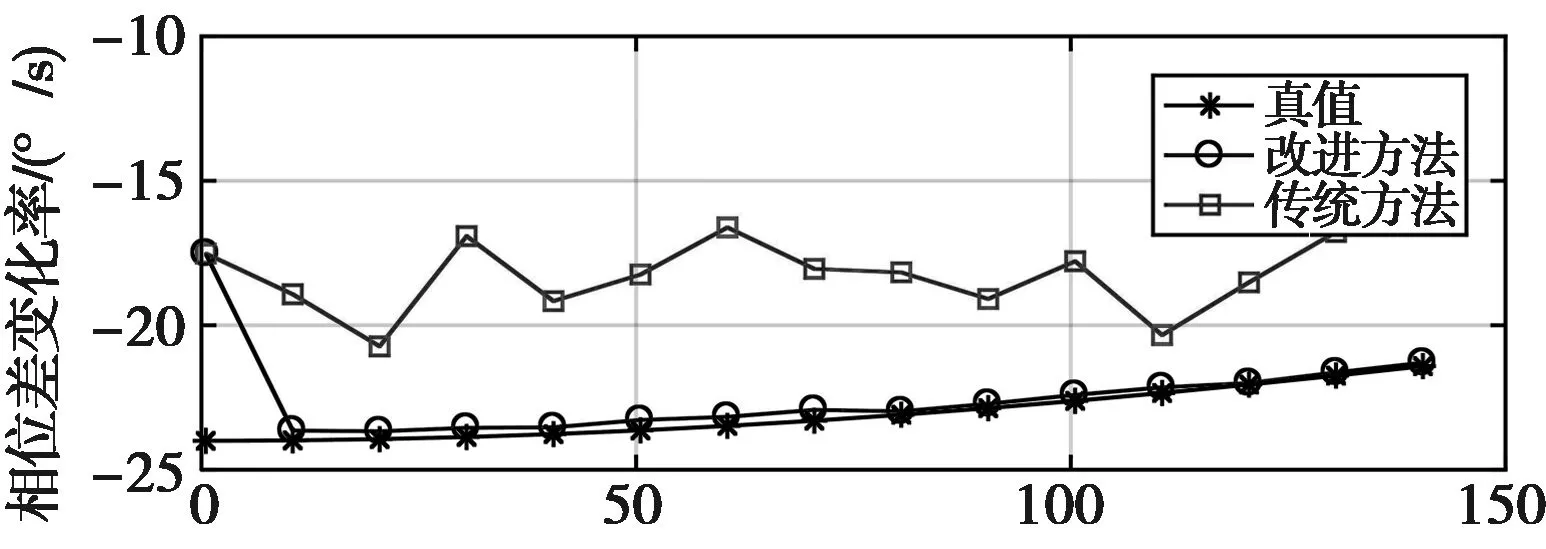
(a) 相位差变化率提取值
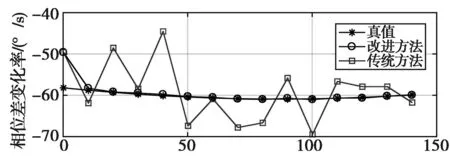
(a) 相位差变化率提取值
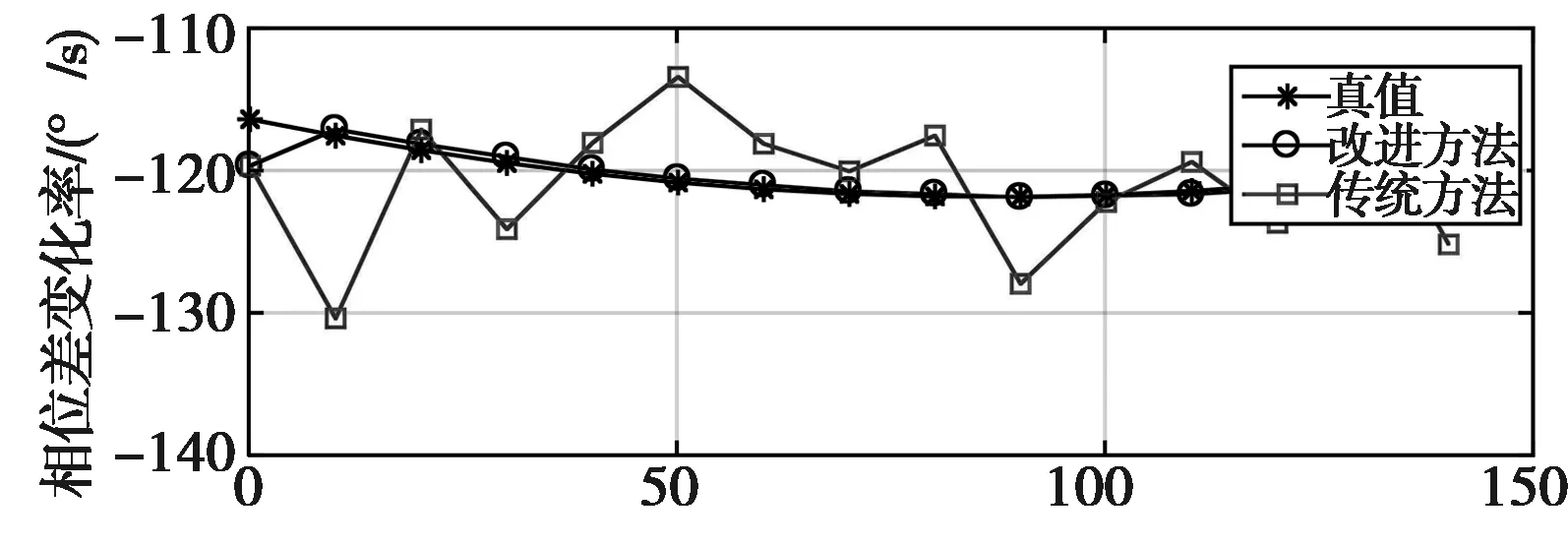
(a) 相位差变化率提取值
由于第1个周期无法采用相邻周期解模糊,其改进的相位差变化率提取方法,除第1个周期与传统方法效果相同外,其余周期的相位差变化率提取误差均小于传统方法。对比3个波段对应的相位变化率提取误差,统计误差均方根(不含第1个周期),结果如表1所示。
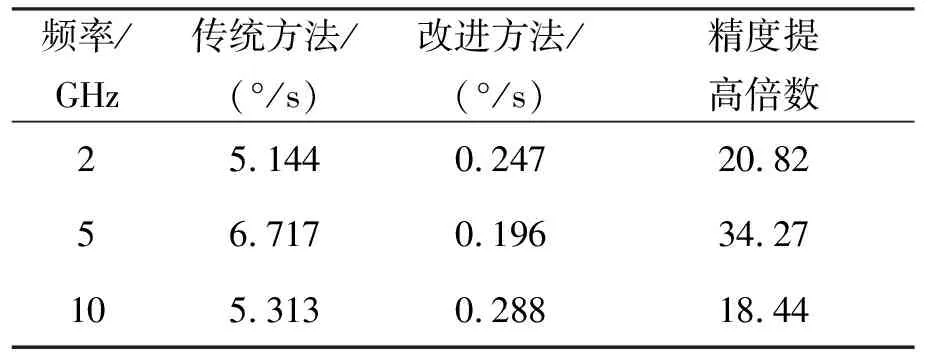
表1 相位差变化率误差统计值对比表
可以看出,改进方法的提取精度比传统方法高十几倍,其中L与X波段提升效果低于C波段,原因在于当其他条件一定时,频率越高,相位差变化量越大,变化率提取受相位测量误差的影响越小,但频率过高造成周期间的模糊数增多,反而降低了周期间的解模糊准确性,因此C波段提取精度改善效果最佳。
5 结束语
本文提出一种采用周期间预测解模糊的方式,利用周期间的信息计算提取相位差变化率,与传统方法进行仿真对比,仿真结果表明改进方法明显高于传统方法,且稳定性良好,为后续相位差变化率定位算法的研究奠定了技术基础。
