一种新型FSK-PSK编码信号特性分析

黄 杰,胡蜀徽

(中国电子科技集团公司第二十九研究所,成都610036)

0 引 言

相位编码信号具有良好的自相关性能,码长较长,但其线性复杂度太低,只要准确获得一段码元就能破解该序列编码。频率编码信号具有大时宽大带宽的特点,能够获得较高的匹配滤波增益,由于能量分布在更宽的频带内,单位频带内的能量幅度较低[1],降低了被截获的概率,但由于其功率谱频点固定,频率易被侦查接收截获识别。

采用相位编码与频率编码组合的信号形式可以大大提高雷达接收机的匹配滤波信号处理增益,在确保雷达探测性能不变的前提下,可减小雷达发射信号的峰值功率,降低雷达信号被侦察到的概率。相位编码方式将原频率编码信号的功率谱展宽,使其峰值下降,加强了其功率谱结构的伪随机性,从而减小了雷达信号被侦察接收机分选、识别的可能性[2],改善了信号的低截获性能。

1 波形设计及信号特性分析

1.1 FSK-PSK信号形式

FSK-PSK(频移键控和相移键控复合编码)信号能够同时实现跳频调相功能,其中FSK跳频序列和PSK调相序列可采用伪随机序列,其复包络可以用下式表示:

(1)

式中,N为子脉冲个数;si(t)为第i个子脉冲发射信号,且

式中,tb为单个码元时间;M为单个子脉冲内码元个数,T=Mtb为子脉冲持续时间;aim为第i个子脉冲内第m个码元的相位信息;Bs=1/tb为子脉冲基带信号的带宽;fi,i=1,2…,N为第i个子脉冲的频率,为随机跳频序列,其中门函数p(t)可表示为

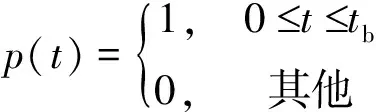
(3)

1.2 基于遗传算法的FSK-PSK波形设计

遗传算法在遗传变异理论的基础上模拟遗传变异的迭代过程,在保持现有结构的同时寻找更优的结构。在FSK-PSK信号设计中,遗传算法的主要目的是全局搜索最优的编码信号,其搜索准则为最小自相关旁瓣幅度,根据此准则最终获得等价优化函数的最小目标值[3],其迭代流程如图1所示。

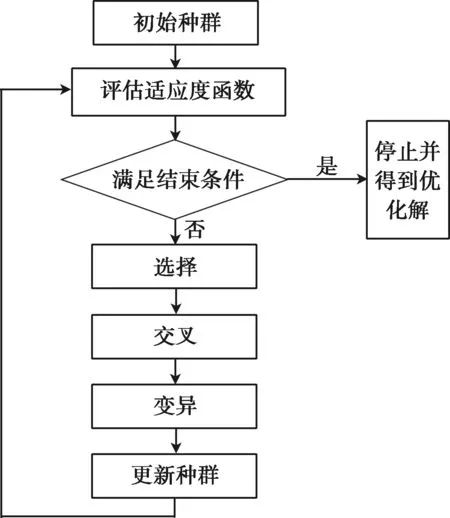
图1 利用遗传算法求解最低旁瓣流程图

步骤1,初始种群的建立与设置。首先设置初始种群的大小,将种群中每个染色体进行序列编码,然后对染色体中每个基因进行赋值,其值随机生成,为不小于0且小于相位个数M、编码长度为N的正整数;

步骤2,代价函数适应度值的评估与分配。适应度值评估使用的代价函数max(|χ(τ)|τ≥t0)(χ(τ)为自相关函数)可以表示为

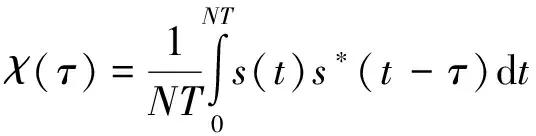
(4)

分配方式为代价函数值越低,分配的概率越大;代价函数值越高,分配的概率越小,以便得到最优信号的相关峰值旁瓣量。

步骤3,遗传算子的修正与选择。通过轮询判断的方式对遗传算子进行选择,运用修正后交叉算子、变异算子分别实现交叉运算和变异运算[4]。同时还要设置遗传算法的终止迭代代数、交叉概率和变异概率,运用到整个群体上。

设仿真参数:信号脉内频率编码点数为4,相位编码为四相编码,码元长度分别为35、70和130时,主副瓣电平比结果如表1所示。

表1 相位编码信号峰值旁瓣电平(单位:dB)

可以看出,经过遗传设计后的FSK-PSK信号的自相关旁瓣电平幅度随着信号码元个数的增加而降低,当码长大于等于70时,旁瓣电平能够降到-19 dB以下,而同等码长的M-Costas编码信号的自相关旁瓣电平只能达到-12 dB,所以经过遗传设计后的编码信号具有低旁瓣优势。

1.3 FSK-PSK信号宽带合成效果

由于FSK-PSK信号在相位编码的基础上引入了频率编码,当频率间隔等于子信号带宽(Δf=Bs)时,信号的总带宽由单一相位编码信号带宽的Bs=1/tb扩展为频率编码带宽,即MBs=M/tb,因此相应的距离分辨率提高了M倍,从而获得了合成宽带的效果[5]。

当频率间隔等于子信号带宽时,FSK-PSK信号的总带宽可表示为

BΣ=(N-1)·Δf+Bs

(5)

式中,N为子脉冲个数即跳频频点数;Δf为调频频率间隔;Bs为子信号带宽。

总带宽为子信号带宽的N倍,具有明显的频率合成后的宽带效应。

设仿真参数:信号脉宽为52 μs;信号脉内频点数N=4;每个频点持续时间为13 μs,每个子脉冲包含M=130个码元;码元宽度为tb=0.1 μs,即对应子信号带宽Bs=10 MHz,载波频率fc=3 125 MHz,跳频间隔Δf=Bs=10 MHz,合成距离向效果如图2所示。

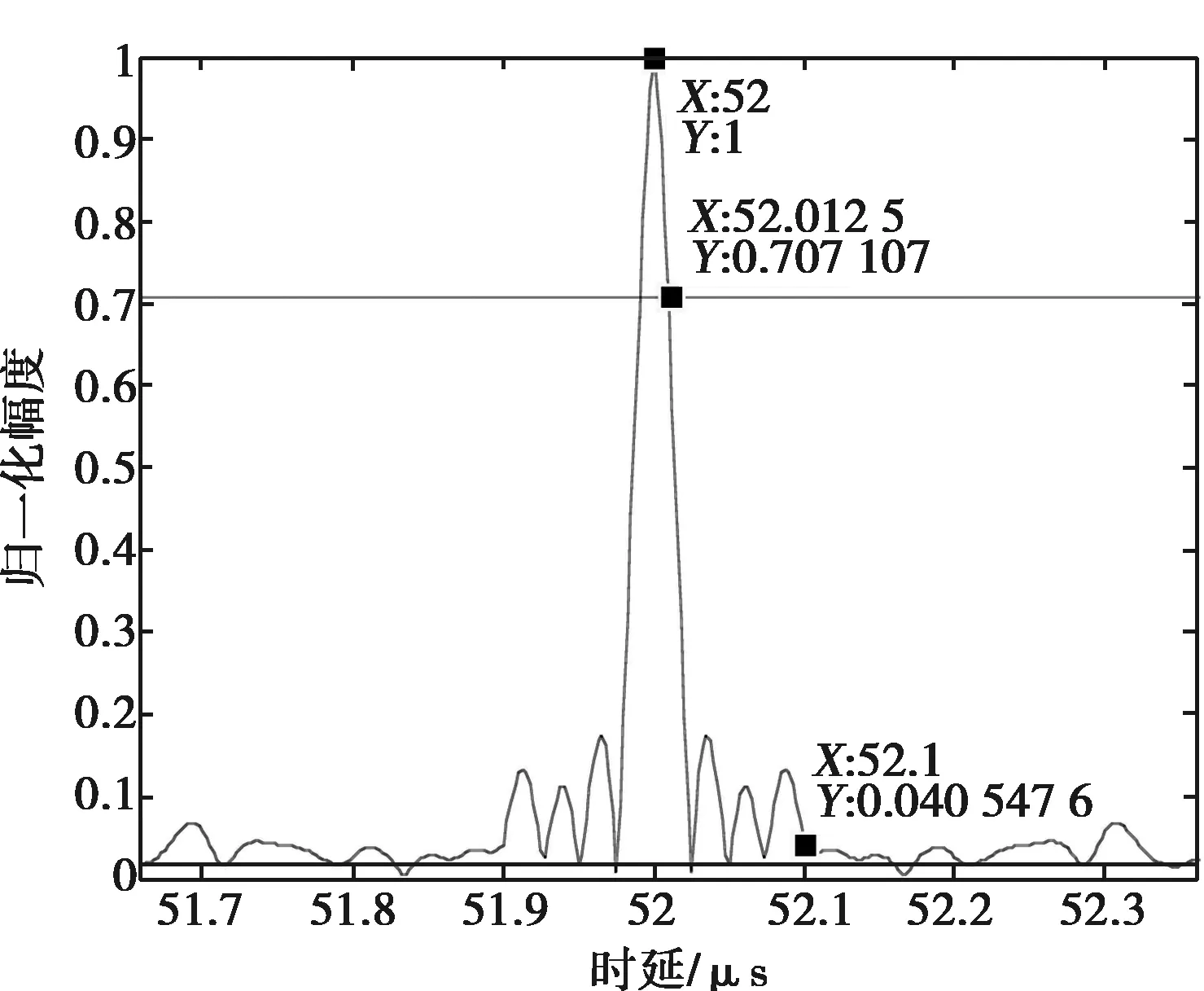
图2 合成距离向效果图

可以看出,距离模糊函数3 dB宽度约为0.025 μs,对应N*Bs=40 MHz的总带宽,距离分辨率提高了4倍。

1.4 多普勒容限分析

由相位编码信号的模糊函数可知其具有多普勒敏感的特性[6],并且随着目标多普勒频率的增加,脉冲压缩输出的主瓣峰值电平降低,严重时会影响雷达对目标的检测能力,所以良好的多普勒容限是相位编码信号需要具有的重要特性。下面分别从信号的码元个数和码元宽度对应的自相关幅度来分析FSK-PSK信号的多普勒容限。

设仿真条件:信号脉内频点数N=4,码元宽度为0.1 μs,每个子脉冲分别包含272、520和1 000个码元,即对应子信号带宽Bs=10 MHz,载波频率fc=3 125 MHz,跳频间隔为Δf=Bs=10 MHz,不同码元个数对应的多普勒容限如图3所示。

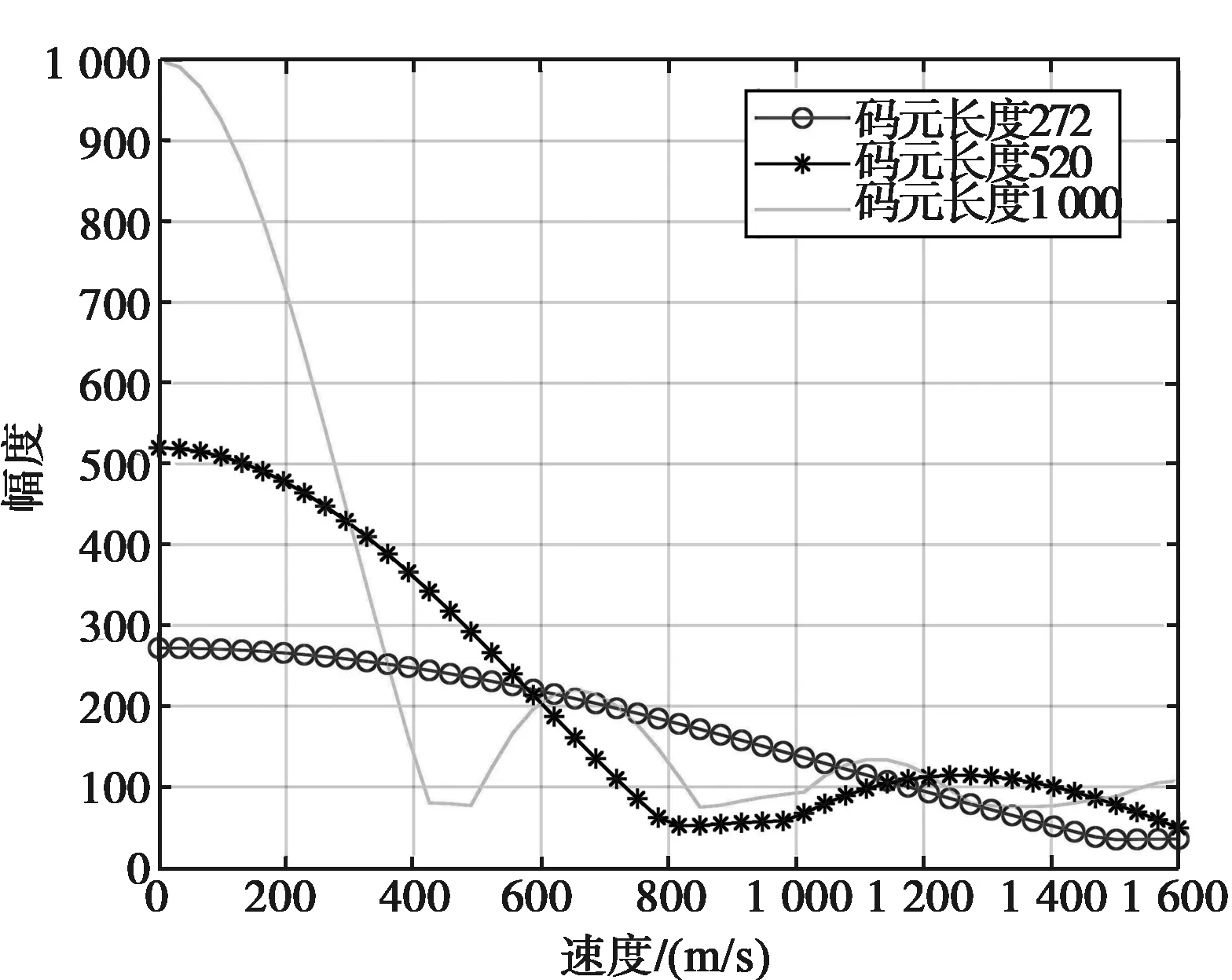
图3 不同码元个数对应的多普勒容限

可以看出,以最大自相关幅度-3 dB为多普勒容限,在码元宽度一定的情况下,随着码元个数的增加,多普勒容忍性降低,当码元个数为1 000时,匹配滤波输出的速度容限约为203.5 m/s,因此较少的码元个数能够获得较高的多普勒容忍性。

设仿真条件:信号脉内频点数N=4,码元宽度分别为0.025 μs、0.05 μs和0.1 μs,每个子脉冲包含300个码元,即对应子信号带宽分别为40 MHz、20 MHz、10 MHz,载波频率fc=3 125 MHz,跳频间隔为Δf=Bs,不同码元宽度对应的多普勒容限如图4所示。

图4 不同码元宽度对应的多普勒容限

可以看出,在码元长度一定的情况下,随着码元宽度的减小,信号对多普勒频移的敏感性会降低,所以设计波形时采用较小码元宽度的信号能够获得更好的多普勒容性。

2 抗干扰特性分析

2.1 低截获性能分析

本节主要分析FSK-PSK复合调制信号的低截获性能。通过对比仿真单一FSK编码信号和不同码元长度的FSK-PSK编码信号的频域特性,验证了后者的低截获性能更好。

仿真条件:FSK信号脉内频率编码点数为4,跳频频率分别为0、80 MHz、160 MHz、240 MHz,对应的频谱图如图5所示。

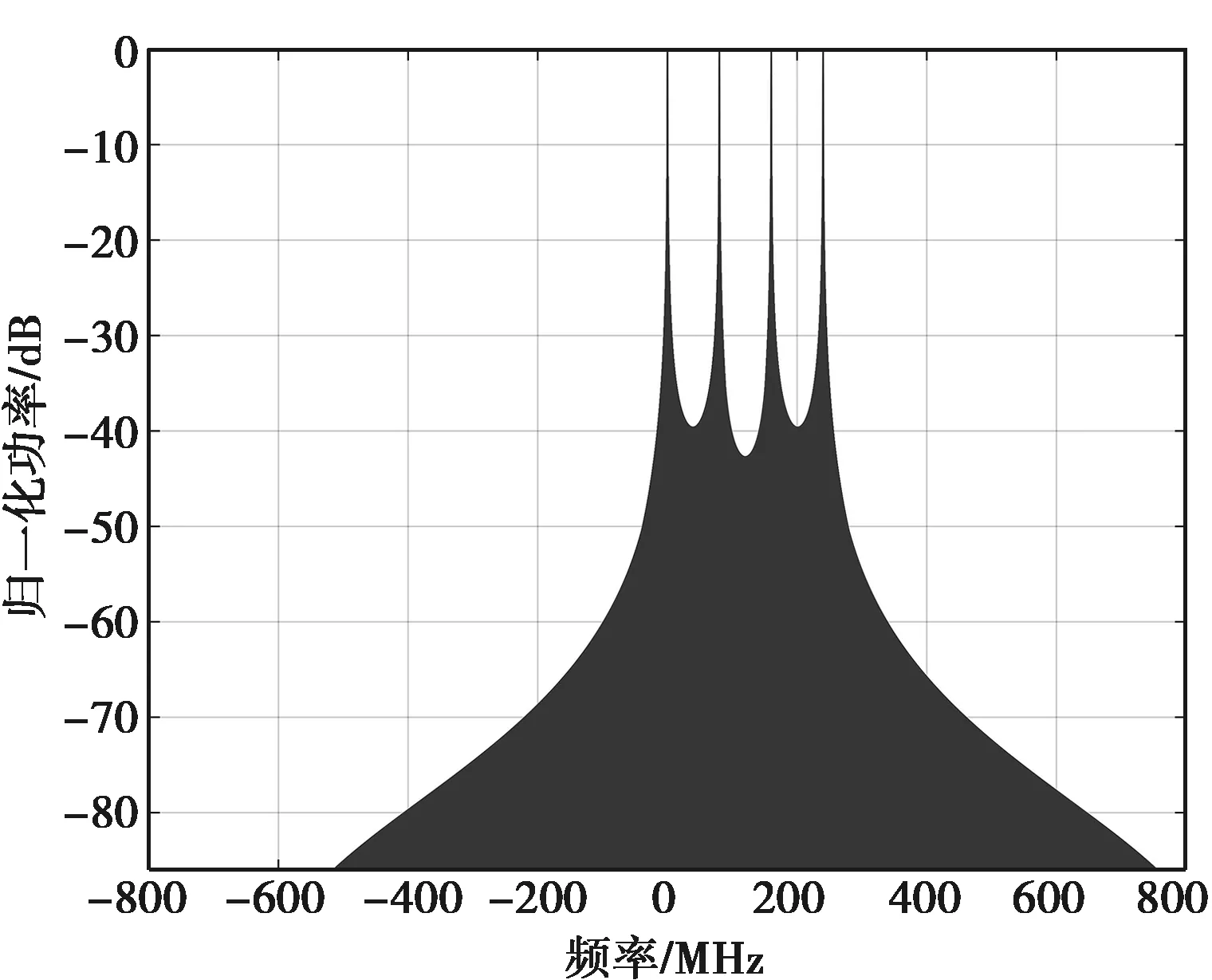
图5 FSK信号频域特性

仿真条件:FSK-PSK信号脉内频率编码点数为4,码元宽度为0.012 5 μs,即对应子信号带宽Bs=80 MHz,每个子脉冲分别包含80、272和520个码元,跳频频率分别为0、80 MHz、160 MHz、240 MHz,对应的频谱图如图6所示。

6.营造氛围，整合风险监管力量。企业风险管理在一定程度上还需要借助外部及内部力量，整合风险管理资源。一是企业在风险管理中要打破职能部门各自为战的壁垒，形成统一指挥、科学调配、信息共享的联动机制；二是企业要在逐步推进内部风险管理审计的前提下，加强与外部监管机构的融合，共同参与，形成有效的监督合力。同时，培养一种风险文化，营造全员参与风险管理的氛围，提高企业适应环境变化、管理风险和规避风险的能力。

(a)码元长度80

由图5可得,采用单一FSK信号的功率谱在频域上集中在数个有限的频点,容易让雷达接收机获得较大的脉冲压缩信号处理增益,易被侦察接收机识别,因而降低了其抗截获性能。

根据图6,将FSK信号脉内单频子脉冲替换为多相编码脉冲,多相编码信号将原频率编码信号的功率谱展宽,使其峰值下降,雷达信号的能量分散在更宽的频率范围内,同时加强了其功率谱结构的伪随机性,从而减小了雷达信号被侦察接收机分选、识别的可能性,改善了信号的抗截获性能[7],增加了电子侦察设备频率分选的难度。

2.2 抗密集假目标干扰分析

本节主要分析FSK-PSK信号抗密集假目标干扰的性能。首先通过遗传算法设计多个正交FSK-PSK信号,然后仿真分析回波信号的互相关特性,由此结果即可分析出该信号的抗密集假目标干扰性能。

假设正交多相编码组有L个信号,每个信号包含N个子脉冲和M个编码相位数,从下面的相位集中选择子脉冲的相位:

φl(n)∈{ψ1,ψ2,...,ψM}

(6)

对于一个码元长度为N、信号个数为L的多相码元集S,能表示为L×N的相位矩阵:

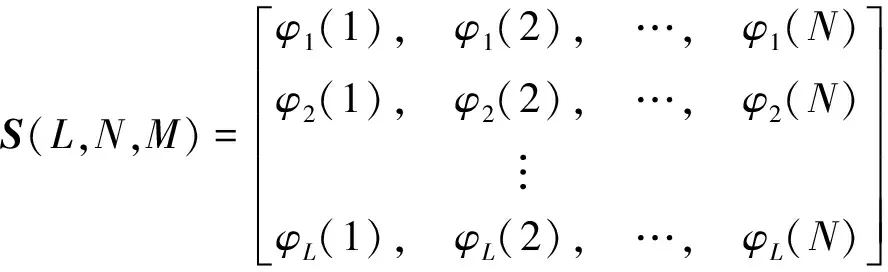
(7)

式中,l,1≤l≤L行相位序列为信号l的相位序列,只能从公式中选择矩阵的所有元素。

根据信号的自相关和互相关特性,可以得到自相关及互相关的表达式,分别为

(8)

(9)

仿真条件:信号脉内频率编码点数为4,码元宽度为0.025 μs,即对应子信号带宽Bs=40 MHz,每个子脉冲包含1 000个码元,载波频率为fc=3 125 MHz,跳频间隔Δf=Bs=40 MHz,通过遗传算法得到FSK-PSK信号的互相关峰值幅度如图7所示。

(a) 信号1与信号2互相关 (b)信号1与信号3互相关

仿真结果表明多个FSK-PSK信号的互相关平均峰值幅度为-35 dB。由于密集假目标干扰是接收雷达信号,然后产生叠加多个假目标信号,当多个脉冲采用正交FSK-PSK信号对抗密集假目标干扰时,相互正交的编码信号通过脉冲压缩无法形成峰值[8],从而达到抑制密集假目标干扰的效果,所以FSK-PSK信号具有很好的抗密集假目标干扰能力。

2.3 抗噪声压制干扰分析

本节主要对比分析单一PSK信号与FSK-PSK信号抗噪声压制式干扰的性能:仿真产生PSK信号,与高斯白噪声信号相叠加;对信号进行数字下变频和匹配滤波,得到噪声压制干扰的处理效果。

仿真条件:PSK调制信号脉冲包含130个码元,码元宽度tb=0.025 μs,即对应信号带宽Bs=40 MHz,载波频率fc=3 125 MHz,叠加的高斯白噪声带宽为40 MHz,噪声压制干扰的匹配滤波效果如图8所示。

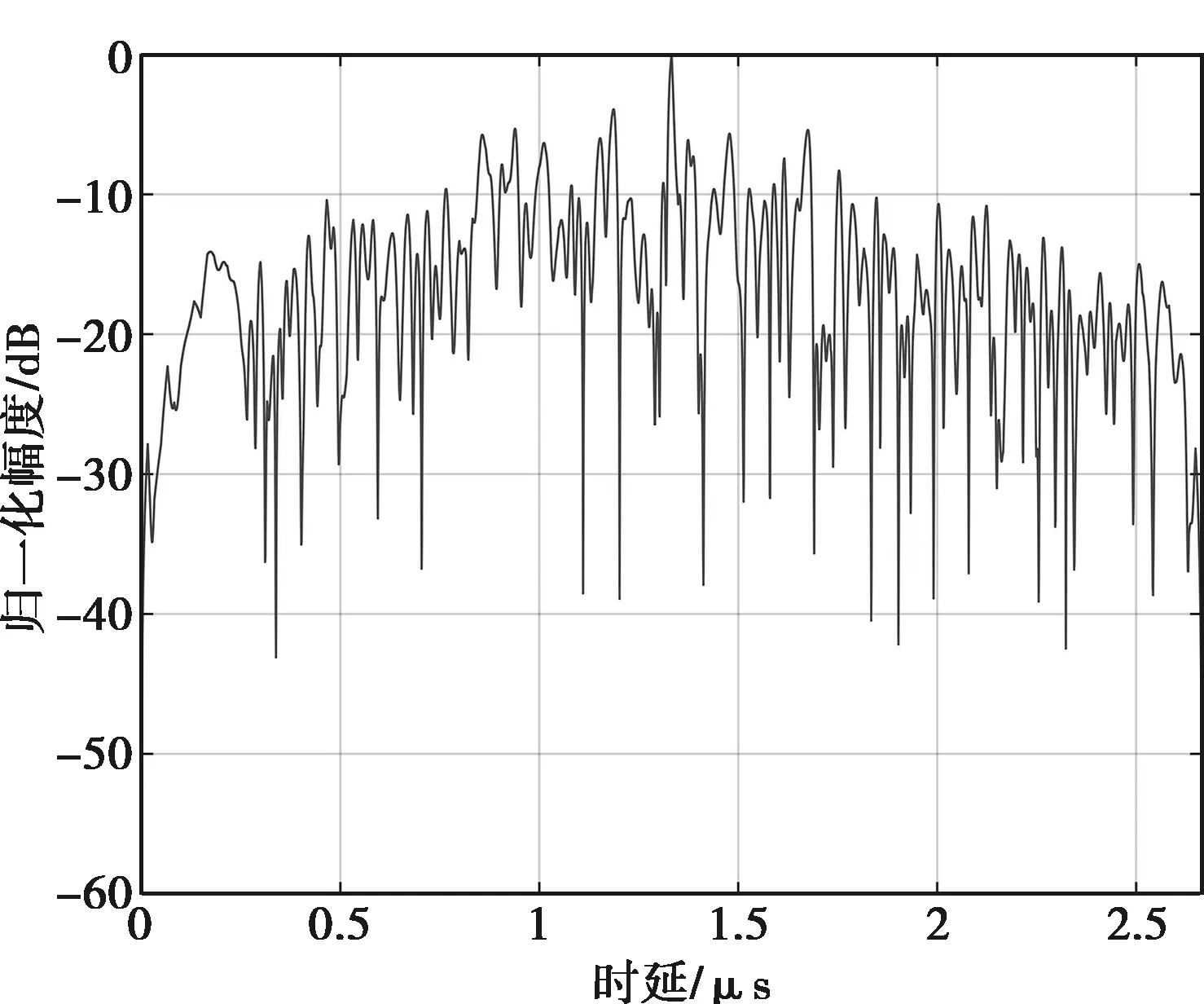
图8 PSK信号噪声压制干扰效果

同理,将FSK-PSK信号与高斯白噪声信号相叠加,根据结果分析该信号的抗噪声压制式干扰性能。

仿真条件:信号脉内频率编码点数为4,每个子脉冲包含130个码元,码元宽度tb=0.025 μs,即对应子信号带宽Bs=40 MHz,载波频率fc=3 125 MHz,跳频间隔分别为80 MHz和120 MHz,对应叠加的高斯白噪声带宽分别为240 MHz和360 MHz。噪声压制干扰对不同带宽的FSK-PSK信号效果如图9所示。

(a)干扰带宽240 MHz(跳频间隔80 MHz)

如图8所示,噪声压制式干扰基本落在PSK信号带宽内,主副瓣电平幅度差只有-5 dB。而FSK-PSK信号的跳频间隔可以做得很大,迫使噪声压制式干扰机将噪声干扰信号的能量均分于整个带宽,从而降低了噪声压制式干扰的有效功率[9]。

如图9(a)所示,当信号跳频间隔为240 MHz时,主副瓣电平幅度差为-10 dB;如图9(b)所示,当信号跳频间隔为360 MHz时,主副瓣电平幅度差为-15 dB,由此可得信号跳频间隔越大,噪声压制干扰的效果越小,从而提高了压制干扰的难度,所以FSK-PSK信号具有优良的抗噪声压制式干扰的能力。

3 结束语

为提升雷达系统的探测能力、目标分辨力、低截获能力和抗干扰能力,本文从频率和相位复合编码设计出发,在已有复合编码方式的基础上,提出了基于遗传算法的FSK-PSK信号设计方法,并对其进行了理论分析和计算机仿真,得到信号的伪随机性、多普勒容限特性、频谱适应性和高分辨特性,证明了FSK-PSK信号具有更好的抗截获能力和抗干扰能力。