一种基于交互多模型卡尔曼滤波的被动协同定位滤波算法研究
2023-09-13张冉,杜清,万岳,朱润
张 冉,杜 清,万 岳,朱 润
(中国船舶集团有限公司第八研究院,南京 211153)
0 引 言
工作在无源探测模式的雷达在捕获目标后,首先根据探测到的目标方位缩小搜索区域来实现对目标的稳定跟踪,然后通过与协同节点的协同定位实现目标位置的估算。由于海面高机动目标协同定位的结果会随测向误差跳变,须通过滤波算法对协同定位后的数据进行平滑处理,使其快速收敛,从而提升目标的定位精度,满足对目标的指标要求。此时,大多采用最小二乘法和卡尔曼滤波算法,配合使用匀速模型和匀加速模型。在机动性不高的情况下,这些算法跟踪精度较好,但是在目标高机动时跟踪精度大幅度下降,甚至会导致目标预测位置与实际位置出现巨大偏差,严重影响对目标打击的引导效能[1]。
由于在大多数情况下目标的运动方式不可知,为了适用于位移、速度和加速度都时刻变化的复杂场景,设计一种多模型自适应适配的机动目标跟踪滤波算法,在跟踪过程中使用若干个模型描述机动目标的不同运动状态,然后再通过加权融合估计系统状态,得出最优估计状态,从而达到模型自适应跟踪的目的[2]。
1 协同定位流程及原理
目标高精度定位与跟踪是雷达系统支持对目标打击的最基本前提,由于在真实环境中,雷达往往工作在静默模式,此时截获的目标只有方位信息,缺少距离项,导致目标指示效果大大降低,所以通常利用协同设备对同一辐射源目标进行测向,测角方位线相交于一点形成封闭三角形实现对目标的协同定位。
协同交叉定位的主要流程如图1所示。在本节点和协同节点各自执行被动探测任务的过程中,对感兴趣的本节点被动探测目标发起协同定位操作,然后将此待定位目标与协同节点共享的被动探测目标进行参数匹配,若多个协同节点被动探测目标均能匹配成功,选择其中定位误差最小的协同节点进行协同交叉定位,同时对定位结果进行滤波并完成误差分析。
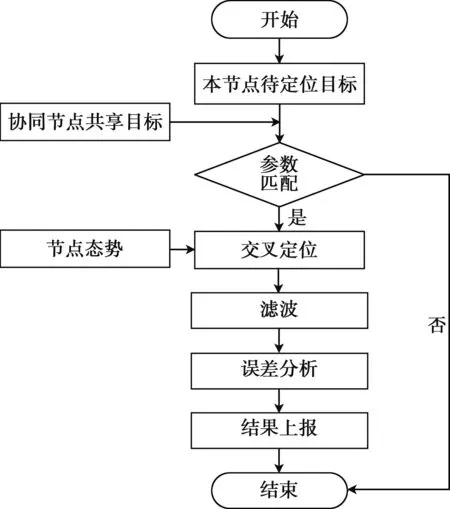
图1 协同交叉定位流程图
协同交叉定位主要通过两个观测平台对目标进行测向,然后根据各个平台测量的方位值以及平台本身的位置信息,解算出目标的位置坐标,但是由于测向误差的存在,交叉定位的结果经常产生跳变,所以在交叉定位后依次对结果进行平滑处理和误差估计,形成与目标指示误差估计方法相匹配的误差数值并上报。
为了将系统观测方程简化为线性方程,本文将交叉定位后的结果作为滤波算法的输入,通过滤波处理得出目标状态的最优估计。但对于位置和运动状态都在不断快速变化的高机动目标,为了获得更准确的定位结果,须利用具有自适应特性的交互多模型卡尔曼滤波算法对其进行滤波收敛。
2 交互多模型卡尔曼滤波算法
通过分析高机动目标的运动特征,将动态目标航迹分为3种模型的组合:匀速运动模型、匀加速动模型和转弯模型[3]。
匀速运动模型可用CA模型表示为
(1)
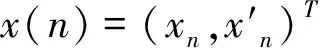
目标匀加速运动的模型表示为
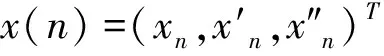
目标转弯模型的角速度为ω,其模型公式可表示为
(3)
传统的最小二乘拟合算法和卡尔曼滤波算法无法对高机动目标进行稳定定位和跟踪,而交互多模型由于可以在目标高机动状态下动态改变匹配模型,因此更适用于复杂的真实场景[4]。交互多模型卡尔曼滤波算法结构流程如图2所示,使用多种滤波器对应多个运动模型,可以看作是多个卡尔曼滤波器的并行化处理,然后通过马尔科夫转换概率在多个模型间进行“软切换”;交互多模型的核心思想是不同的估计对应不同的权重值,权重由模型概率确定,因此可以把它的估计结果看成一个由不同模型交互而得的混合估计。
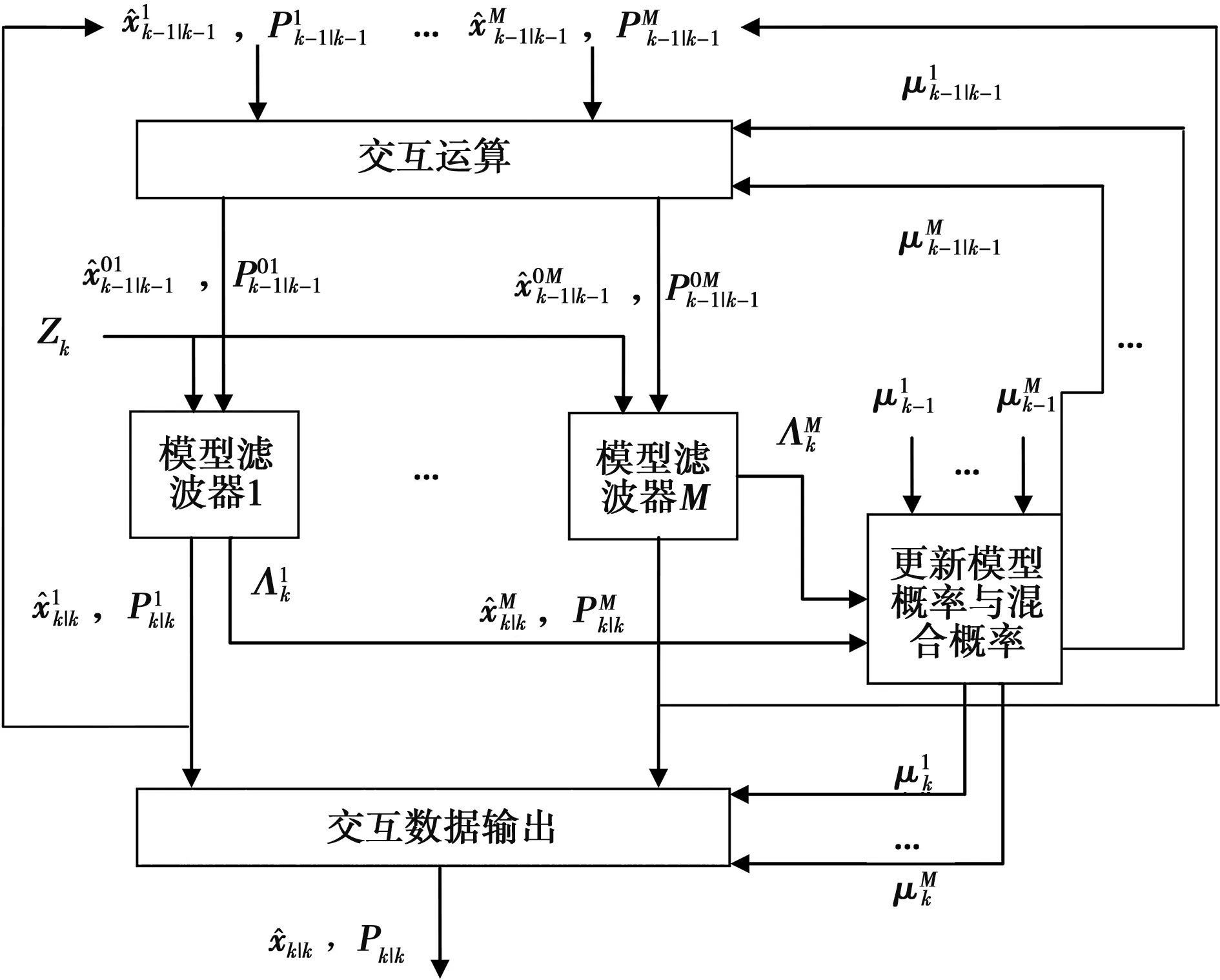
图2 交互多模型算法结构流程图
算法步骤如下:
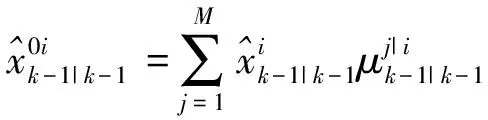
(4)
(5)
状态的预测值及其协方差为
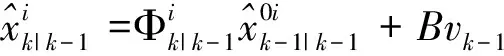
(6)
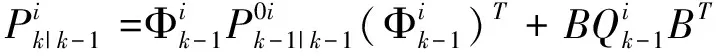
(7)
卡尔曼滤波器估计值为
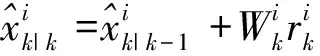
(8)
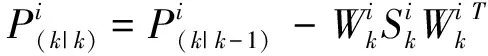
(9)
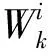

(10)
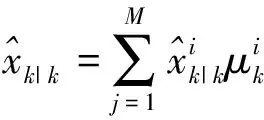
(11)

(12)
3 仿真试验
雷达工作在被动探测模式下的测向精度对副瓣抑制能力和信号连续截获有较高要求,而测向精度直接关系到定位精度,同时目标与观测平台之间的相对位置分布也会影响定位精度,这种误差的分布常用定位精度几何稀释度表示。为保证定位精度,应对观测平台的测向误差、观测平台之间的距离和目标相对于观测平台的夹角有一定约束,除了基线长度不能太短,还要求交叉定位形成的三角区域尽量为规则三角形。
本文仿真设置测向误差为0.5°;基线长度为20 km,目标距离观测节点1的初始距离为40 km,初始方位角为14.5°,目标相对观测节点2的初始方位角为345.5°,初始状态如图3所示。目标开始做高机动航行,整个过程模拟了一个目标在不同时间区间多种运动状态组合的场景。
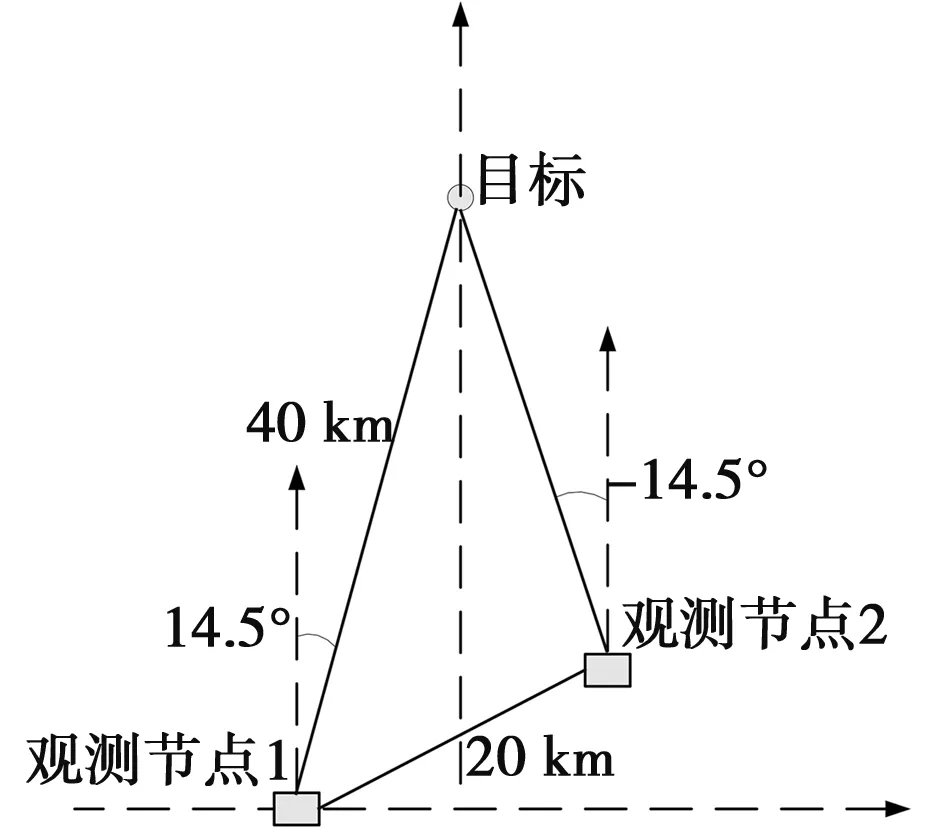
图3 交叉定位示意图
为了验证算法的性能,同时对比常规卡尔曼滤波定位效果,实验通过Matlab软件仿真来测试,主节点和协同节点在同时捕获到同一目标的情况下,对目标进行交叉定位,根据雷达天线扫描间隔形成采样间隔,生成采样点迹。
为了模拟高机动性目标,把整个航迹分为5段,具体参数设置如下:
(1)第1段航迹S1(0~100点),观测目标作低速匀速直线运动,航速10 m/s,持续时间2 000 s;
(2)第2段航迹S2(101~150点),观测目标作慢速转弯曲线运动,航速10 m/s,加速度0.2 m/s2,持续时间1 000 s;
(3)第3段航迹S3(151~225点),观测目标作中速匀速直线运动,航速14 m/s,持续时间1 500 s;
(4)第4段航迹S4(226~275点),观测目标作快速转弯曲线运动,航速14 m/s,加速度0.5 m/s2,持续时间为1 000 s;
(5)第5段航迹S5(276~350点),观测目标作快速匀速直线运动,航速为23 m/s,持续时间为1 500 s。
图4、图5分别给出了常规卡尔曼滤波算法的定位滤波效果和滤波误差均值曲线;图6、图7分别给出了交互多模型卡尔曼滤波算法的定位滤波效果和滤波误差均值曲线,其中雷达的探测值是在真实值的基础上叠加了由测向误差导致的定位误差。
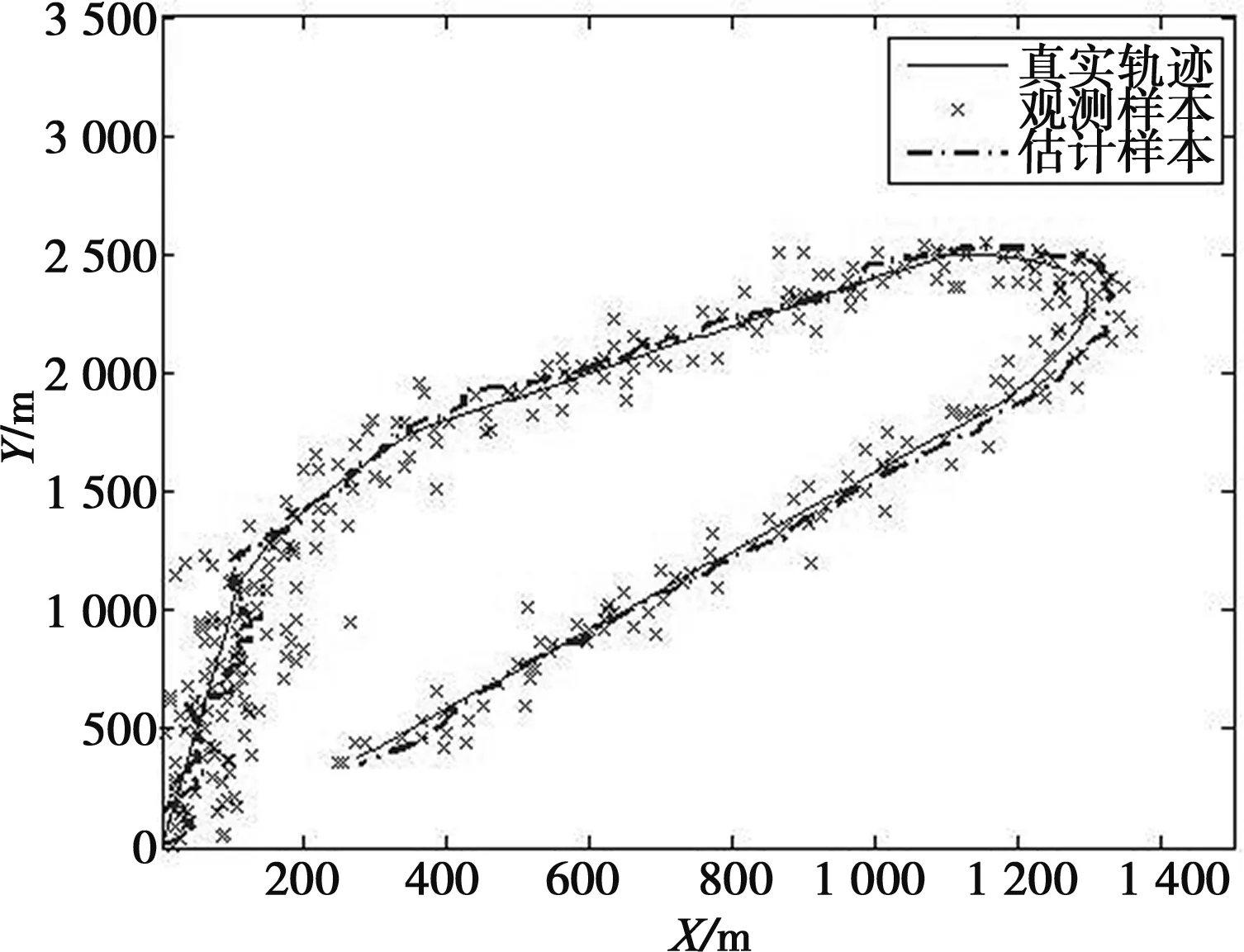
图4 常规卡尔曼滤波效果
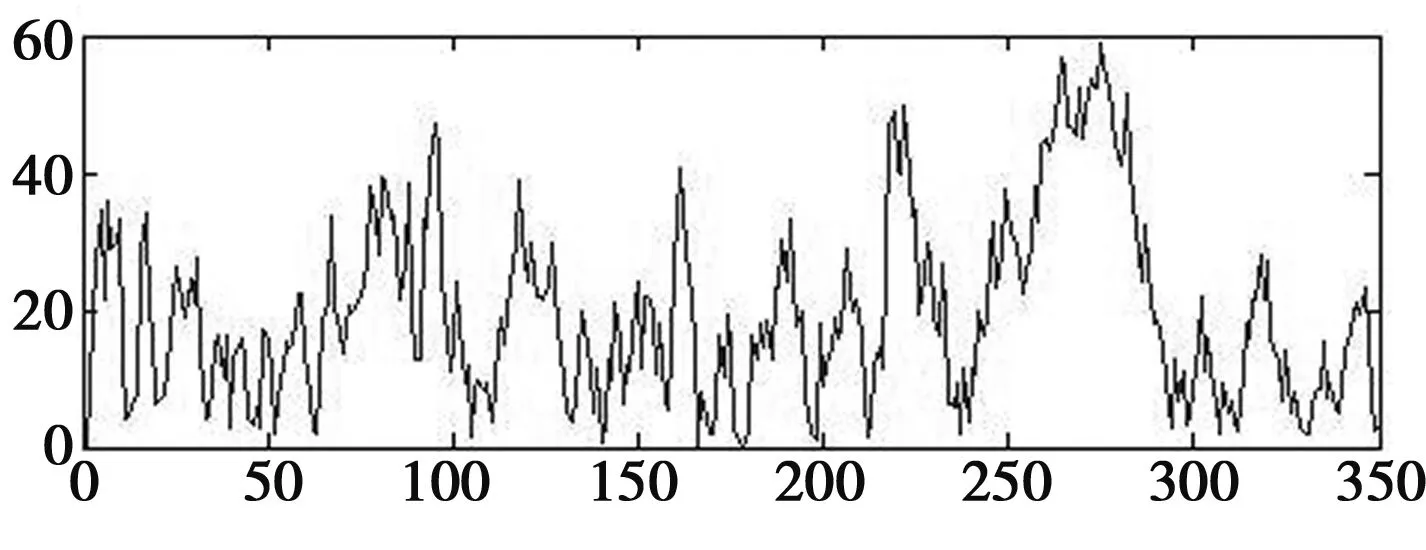
(a) X方向

图6 交互多模型卡尔曼滤波效果
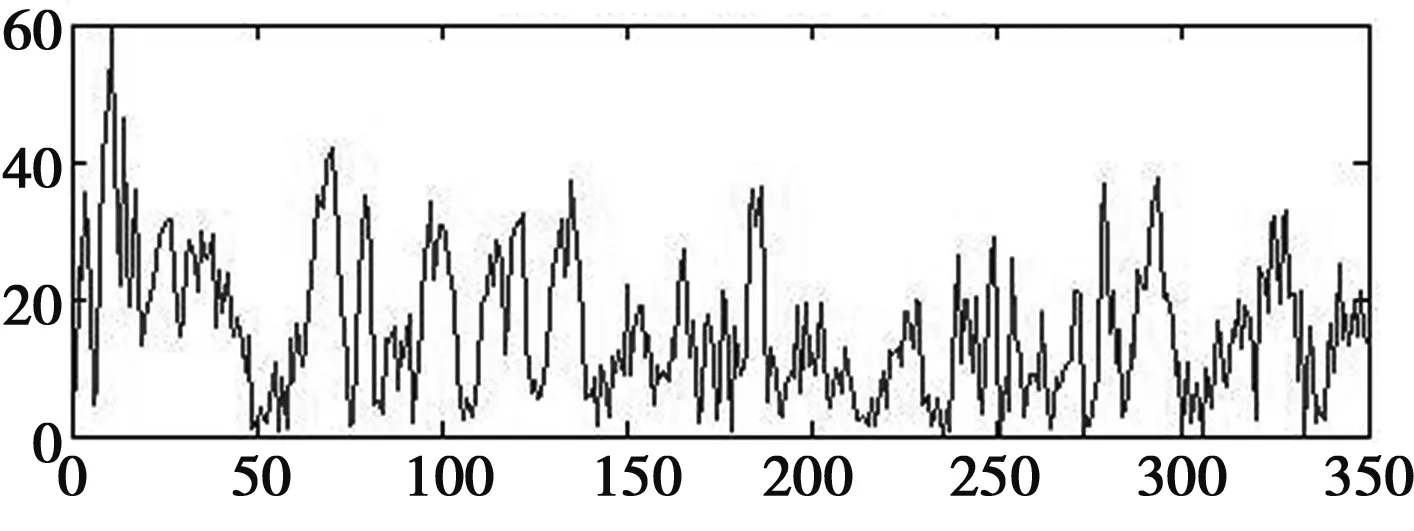
(a) X方向
表1统计了5段航迹的滤波误差标准差均值。可以看出,在目标刚开始作匀速直线运动时,常规卡尔曼滤波算法更容易收敛;随着目标开始作慢速转弯曲线运动,常规卡尔曼滤波算法的滤波效果开始下降,但是与交互多模型卡尔曼滤波算法的性能差别不大;当目标作快速转弯曲线运动时,常规卡尔曼滤波算法的滤波效果明显下降。

表1 五段航迹的滤波误差标准差均值统计
4 结束语
本文算法对机动性能强的目标有较好的跟踪滤波效果,尤其在掺杂大量匀加速运动和曲线运动时,往往能保持住定位和跟踪精度。但是交互多模型算法在机动目标定位跟踪时能发挥有效作用的前提是要设置和实际运动状态相一致的运动模型,在缺乏先验信息支持时,如果采用固定不变的模型组合形态,大概率会在实战过程中丧失作用,所以须积累大量的实测数据,以建立较完备的模型集合,通过各模型之间的交互融合完成系统状态估计、各种运动形式的机动目标定位跟踪任务,同时也可以提升对目标指示能力。
