圆柱桥墩局部冲刷机理

梁浩然，胡亮亮，袁 浩

（1.重庆交通大学河海学院,重庆 400074；2.重庆交通大学航运与船舶工程学院,重庆 400074；3.重庆交通大学重庆西南水运工程科学研究所,重庆 400016）

0 引言

由于受到圆柱绕流的影响,桥墩这类阻水建筑物周围的水流会形成局部冲刷。这样的冲刷就会导致桥墩的埋置深度减小,长此以往随着基础埋深的逐渐减小桥墩的稳定性就会大大降低,这会对桥身造成巨大威胁,造成巨大的安全隐患。

1 桥墩冲刷研究现状

在计算桥墩局部冲刷时,主要考虑桥墩特征、水流特征以及河床质特征的影响。目前的实际工程中,桥墩附近的环境比较复杂。其中水流结构和泥沙运动机理还没有严格的公式可以计算预测,故大多实际工程采用经验公式[1]进行计算。近年来也有研究者汇总全国的研究成果得到了新的计算公式[2]。此外张佰战等[3]通过能量平衡的原理,通过比较不同粒径下的点群分布得出了新的桥墩局部冲刷计算公式。周玉利等[4]综合流体因素和流动因素,总结出了新的简化公式。韩赛骞等[5]总结出了潮流作用下的桥墩局部冲刷公式。桥墩局部冲刷公式见表1。本文基于经典的Melville-Chiew[6]冲深经验公式得到了新的圆柱桥墩在大流速下的冲刷深度修正公式。

2 试验布置与方法

试验水槽长20 m、宽1 m、深1.1 m,水槽模型示意图见图1,测点布置图见图2。水槽中部为沙槽,沙槽长2 m、宽1 m、深40 cm,试验采用的细沙中值粒径d50=0.29 mm。试验设置有4个流量和4个水深下的共16 个工况,每个工况包含192个测点,每个测点数据测量1分钟。

图1 水槽模型示意图

本试验使用的Nrotek AS公司的ADV（小威龙,最大频率200 Hz）是一种单点、高分辨率流速仪,它依据声学多普勒效应使用一个发送器与三个接收器接收经水体中固体微粒散射后产生的频率差信号,通过信号处理软件分析、合成,便可得到采样水体的三维水流速度[7]。试验待桥墩局部冲刷基本稳定后对桥墩附近流速场进行测量。冲刷结束后再通过红外线距离探测仪获得地形资料。

3 桥墩冲刷结果与讨论

冲刷地形结果图见图3,结果表明,冲刷坑形状呈倒圆锥形分布,最大冲深分布于边界层与桥墩分离处,本试验中地形冲刷呈对称分布,且冲刷结束后会形成燕尾形的沙丘。冲刷结果表明桥墩绕流关于x轴对称；受桥墩阻水影响墩前水流分成了两部分：当y*/H＞0.6时,部分水流直冲桥墩,在墩前产生向上的涌流；当y*/H＜0.6时,部分水流很明显得产生了下冲的趋势形成了墩前下潜水流[8]。其中y*是水流平面在y方向上距离y轴的距离、H是水深。此外,墩后还会形成一个竖向漩涡区,产生泥沙堆积。桥墩局部冲刷的主要动力是墩前大尺度的下潜水流与横向环流[8]。下潜水流在冲刷坑附近沿着桥墩两侧生成漩涡,漩涡呈马蹄形分布,其使得河床泥沙向两侧及下游延伸；漩涡分布对称且不断地从桥墩后方释放出来,这样的尾流旋涡会促进桥墩下游的冲刷进一步发展,最后形成燕尾型堆积沙丘。

图3 H=12 cm时冲刷坑地形图

3.1 最大冲深

定义最大冲深h*=h0/D,其中为实测最大冲刷深度,D为桥墩尺度（直径）；根据系统实验,最大冲深与流场、下游水深变化关系见图4、图5。

图4 最大冲深与水深的关系

图5 最大冲深与流量的关系

分析图4、图5结果表明,不同流量条件下,随着水深增加流速减小最大冲深均随着水深的增加而减小,流量越大、水深越浅时其规律越明显。这是由于墩前的下潜水流将墩前部的扇形区域冲刷,形成冲刷坑,随着水深逐渐减小,水流逐渐变得混乱,水流的紊动能不断增大,下潜水流具有更强的能量卷起更多泥沙；流速逐渐增大时,水流流速增大,墩前的下潜水流具有更强的动能,墩前的冲刷坑更深,且墩后的淤积也更高。系统实验表明z方向上的紊动能大大强于另外两个方向,且图6表明水深变浅后更强的紊动能使得其在墩前的马蹄形范围内卷起更多的泥沙；下潜水流的冲击深度增大,呈现出最大冲深增大的趋势。

图6 流量Q=200 m3/s时不同水深下的z方向的紊动能图

3.2 最大冲宽

定义最大冲深L*=L/D,其中L为实测最大冲刷宽度,D为桥墩尺度（直径）。

根据系统实验,冲刷扩散角与流场、下游水深变化关系见图7,最大冲宽与流速水深的关系见图8。其表明最大冲刷宽度受水深的影响较为明显,由于桥墩绕流的挤压作用使两侧流的流速加大形成局部水面的跌落与回升,桥墩末端形成尾流涡旋区[8]。根据圆柱绕流涡的脱落模式[9-12],由于涡的自旋会消耗能量,而行进流速大时,涡的自旋时间变短,这使得涡可以携带泥沙运动到更远的位置,即冲刷的水平距离变远。涡彼此接近时的相互旋转碰撞也会消耗能量,大的流速下这个过程会变短,这使得能量消耗进一步减小。实验时可以明显地观察到桥墩后方存在对称分布的、吸附在桥墩上的涡；涡在脱离桥墩时具有横向扩散的趋势,高流速下吸附在桥墩上的涡具有更强的扩散趋势,随着这个横向扩散趋势的增大,扩散角度增大,被挤压的水流远离桥墩的角度增大使得冲刷的范围也随之增大。

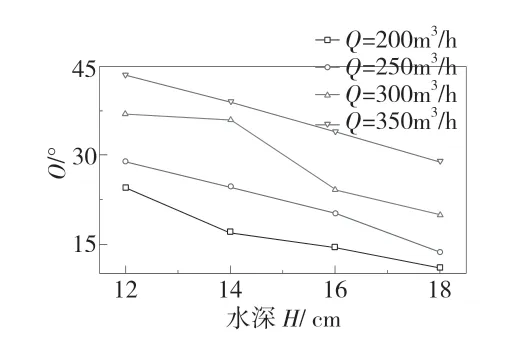
图7 不同流量下冲刷扩散角与水深的关系

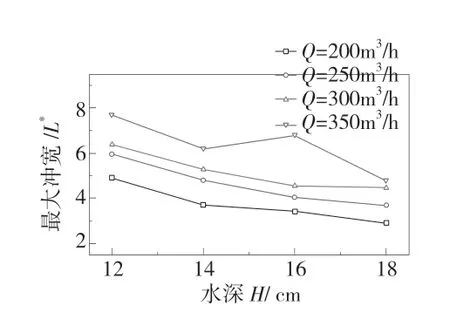
图8 不同流量下最大冲宽与水深的关系

z方向上的紊动能是桥墩冲刷过程中的重要影响因素。紊动能随水深变化图见图9,其表明水深对紊动能的变化影响较大。水深对于最大冲宽的影响实质上是水深变化引起了紊动能的变化。随着水深的降低,绕柱水流在桥墩后方汇集并逐渐变得杂乱。紊动能增加使得冲深范围扩大,最大冲宽随即扩大。

图9 相同流量下y=0平面紊动能变化图

对系统实验的最大冲宽实测数据进行分析,发现其轨迹与Γ分布较为相似：

利用Γ分布对水深和流量与最大冲宽的关系进行线性拟合得到最大冲宽L*与水深H和流量Q的关系为：

将本系统实验数据代入公式得到最大冲宽误差分析图见图10,其拟合较好。

图10 最大冲宽误差分析图

3.3 修正公式

经验公式一般是通过大量的实验数据和天然观察资料拟合而来,但为了安全起见往往按照数据的外包线确定公式参数,其结果一般大于资料的平均值。在本文的实验工况下,经验公式计算结果与实测数据的相差较大。于是为了找到更符合本研究情况下单圆柱桥墩的最大冲深经验公式,引入了经典的Melville-Chiew[6]经验公式,t时刻的冲深刷深度ys（t）：

根据不同的桥墩直径与水深的比值的经验系数KhD：

基于流速与起动流速的比值的经验系数KI：

基于桥墩直径与泥沙中值粒径的比值的经验系数Kd：

式中：d50为泥沙中值粒径；Kt为时间因子；D为桥墩直径,h为水深；V为流速；Vc为起动流速；ys为平均冲刷深度。

使用Melville-Chiew经验公式得到的差异分析图见图11。

图11 Melville-Chiew公式差异分析图

通过对比计算值与实测值发现,在流速较小时,Melville-Chiew经验公式吻合较好,但为了找出更为符合大流速下的圆柱桥墩冲深公式,于是根据最大冲深与流量、水深和流速以及中值粒径的关系引入常数Ψ：

式中：Q为流量；H为下游水深；v为流速；d50为泥沙中值粒径,符号的单位均为国际制基本单位。

基于Melville-Chiew经验公式得到符合本系统实验下的桥墩冲刷最大冲深修正公式为：

式中：h*为本文定义的无量纲最大冲深。

Melville-Chiew经验修正公式误差分析图见图12,经过修正公式得到的结果更为符合大流速下单圆柱桥墩系统实验结果。本文研究的最大冲深h*为实测最大冲深与桥墩直径的比值,为无量纲数。为了使之与通用的冲刷深度表述统一,将公式修改为：

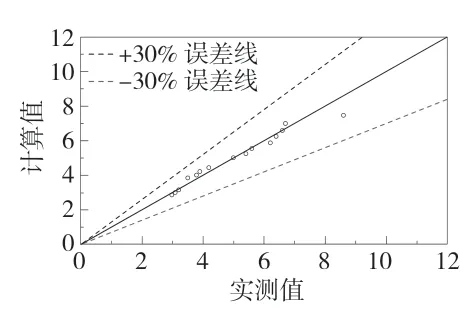
图12 修正公式误差分析图

式中所有符号的单位均为国际制基本单位。

4 结论

本文基于系统实验,探究了圆柱桥墩冲刷机理,得到以下结论：

（1）最大冲深分布于边界层与桥墩分离处,冲刷地形为倒圆锥形且呈对称分布。形成墩前冲刷的原因是墩前的下潜水流卷起了泥沙；而相应的,在墩后位置产生了向上的涌流,这股涌流携带着泥沙形成了墩后的淤积。

（2）桥墩附近绕流的挤压作用使两侧流的流速加大从而形成了局部水面的跌落和回升,在桥墩后方尾流形成了涡旋区。流速大时,涡旋区内的涡能量大、流场紊动能大,水流扩散的角度增大,被挤压的水流远离桥墩的角度增大使得冲刷的范围随之增大。

（3）本文给出了桥墩冲刷的最大冲宽的拟合经验公式；此外本文还对比了国内其他研究者的桥墩最大冲深计算公式,基于Melville-Chiew公式,提出了更为符合本文工况下的圆柱桥墩在较大流速下的最大冲深修正计算公式。