基于改进Elman神经网络的发电厂发电量预测

潘璐璐，茅大钧*，陈思勤

（1.上海电力大学自动化工程学院，上海 200090；2.华能国际电力股份有限公司上海石洞口第二电厂，上海 200942）

0 引言

发电厂的任何管理行为要突出效益优先的原则，不管是安全效益、经济效益还是社会效益［1］，作为发电厂生产活动的第一步，燃煤采购的效益显得尤为重要。因为发电计划存在一定滞后性，目前我国大多电厂的采购策略是以发电量预测为指导，然而，电厂一般采用的预测方式是对比往年发电量的简单预测，没有建立相应科学模型［2］，无法准确指导燃煤采购等生产活动，不利于发电厂的日常运营。及时准确地掌握未来发电趋势变化，可以为企业的煤炭需求分析提供有效支持，有效降低发电成本，帮助火电企业制定出合理的采购决策［3-4］。

现在国内外对于火力发电量的研究大多是面向地区的［5-8］，针对发电厂本身的研究数量非常有限，文献［9］利用最大互信息系数求取发电厂发电量各影响因素之间的关系，进行非线性变量的筛选，提高了预测的准确度；文献［10］提出了一种火电企业短期日发电量预测模型，采用将极限学习机（Extreme Learning Machine，ELM）和递归预测相结合的方法，提高了发电企业未来4 d～7 d发电量的预测准确度；文献［11］建立了一种动态3 次指数平滑法预测模型，提高了发电厂月发电量预测的精确度，对于电厂来说也有较高的实用性；文献［12］对移动平均法和长短期记忆网络（Long Short-Term Memory，LSTM）分别取权重进行组合，用于预测电厂中长期发电量，一定程度上提高了发电量预测的精度。

目前，尽管发电厂发电量预测研究已经有了一定成果，但是仍然存在一些问题。首先，发电厂的发电量受到多种因素的影响，影响因素的选择与整体预测结果有很大相关性，但是分析角度不同，影响因素的筛选结果也会有很大差别，影响因素选取较少，预测结果会产生明显的误差，但是影响因素并不是考虑得越多越好，因为很多因素并不是单独存在的，因素之间也有相互作用的关系，当数据信息增多，多维度的影响因素之间的关系会掩盖掉有效特征之间的耦合，影响有效特征对预测指标的映射［13］，从而影响最后的预测结果，并且考虑太多的影响因素，可能会增加算法难度造成预测数据出现错误。其次，针对发电厂月度发电量的预测方法，因为数据量较小，易造成模型学习精度不够导致预测结果不准确。

因此，本研究旨在探究上述问题并提出相应解决方案，提出一种基于改进Elman 算法的发电厂发电量预测方法。电量预测的核心是历史用电量数据［14］，将历史发电量数据集分解为不同模态分量，并根据特征重新组合，以滚动数据集的形式对模态进行预测，并将各部分预测结果综合得到最后的预测结果。整个流程中，不仅充分利用原始时间序列本身的特征，避免了对发电量影响因素的直接分析，还通过使用滚动时序模型，在原始数据量的基础上增加了模型输入的数据量。采用的基于天牛须搜索（Beetle Antennae Search，BAS）算法改进Elman 模型，相较于传统Elman 模型能够更加高效地进行预测，且具有更好的全局优化能力，能够在实际中发挥重要作用。

1 VMD变分模态分解

因为发电厂的发电量数据具有明显的季节波动性，适合通过数据分解手段对其进行处理。变分模态分解（Variational Mode Decomposition，VMD）能够将历史发电量数据分解成多个频率不同且相对平稳的子序列，从而有效降低发电量数据的复杂度和非线性［15-17］。具体分解迭代步骤如下：

1） 将原始发电量数据f(t)分解为M个离散的本征模态分量（Intrinsic Mode Function，IMF），并设为Vm。

2） 通过Hilbert 变换求解每个分解模态的中心频率ωm和带宽，要求所有模态之和等于原始信号，且各分解模态的估计带宽之和最小［18］。约束变分表达式为：

式（1）中，{Vm}为分解出的m个模态分量合集；{ωm}为各模态对应的中心频率合集；“*”为卷积符号；δ(t)为狄拉克函数；f(t)为原始发电量数据序列。

3） 引入拉格朗日乘法算子λ和二次惩罚因子α，使约束性变分问题无约束化。

4） 采用交替方向乘子更新迭代v̂m、ωm和λ，得到各模态及其对应的中心频率：使用初始中心频率和带宽，对每个分解模态的辅助变量进行求解；将所有分解模态的辅助变量相加，得到全局模态；根据全局模态，更新每个分解模态的辅助变量。

5） 如果分解模态已经收敛，则结束迭代，将最后一次迭代的分量结果v̂m和其对应的中心频率ωm作为最终结果输出，精度收敛判据ε＞0；如果不满足式（2）的条件，则返回到步骤2），继续进行计算。

式（2）中，v̂m和ωm分别为最后一次迭代的分量结果和其对应的中心频率；n为当前迭代次数；N为最大迭代次数。

2 BAS改进Elman神经网络

2.1 Elman神经网络

Jeffery L.在1990 年提出的Elman 神经网络，是一种反馈式的动态递归神经网络，其与前馈式神经网络不同之处在于，它增加了承接层，使得网络能够内部反馈、存储和利用过去时刻输出信息，从而充分利用历史数据，进而更好地适应数据动态信息特征，提高预测精度［19］。

Elman神经网络由4个主要组成部分组成，包括输入层、隐含层、承接层和输出层，这些部分相互作用，共同完成神经网络的计算和预测任务［20-21］。每一层的神经元个数需要根据数据特征和反复对比得出，其结构如图1所示。

图1 Elman神经网络的拓扑结构Fig.1 Topology of Elman neural network

Elman神经网络的基本数学模型如下：

式（3）-式（5）中，u为输入层向量；x为隐含层向量；xc为承接层向量；y为输出向量；w1、w2、w3分别为神经网络不同层之间的连接权值；f(x)和g(x)分别为隐含层和输出层的传输函数；α为自反馈因子，一般α∈[0，1]［22］。

Elman神经网络误差指标函数E(k)为：

式（6）中，y(k)和y͂(k)分别为实际和预测输出值。

Elman 神经网络学习就是通过不断迭代，使得误差指标函数最小，Elman 神经网络隐含层的传递函数采用tansig 函数，输出层的传递函数采用purelin函数［23］。

2.2 天牛须搜索算法

天牛须搜索算法主要步骤如下［24-25］：

1） 假设天牛朝向都是随机的，可以生成随机位置向量来表示和标准化它。

式（9）-式（11）中，δt为t时刻的步长；f为待优化的函数；sign为符号函数；ηd为质心与须之间的距离衰减系数；d0为距离常数；η为步长衰减系数。

2.3 天牛须改进Elman算法

由于传统的Elman 神经网络运行时间较长，且容易陷入局部最优，因此，本文采用天牛须搜索算法对Elman 神经网络进行优化，利用天牛须搜索算法寻找Elman 的最优权值和阈值组合，从而构建一个快速精确的预测模型，优化过程如图2 所示，其具体步骤如下［26-27］。

图2 BAS改进Elman神经网络流程Fig.2 Flow of optimizing Elman neural network with Beetle Antennae Search

Step1：建立Elman模型，设定模型的结构。

Step2：设置BAS算法的搜索范围和步长。

Step3：计算BAS 算法的适应度值。其中，适应度评价函数f为均方根误差（Root Mean Square Error，RMSE）。适应度最小时对应的位置为当前最优解。

Step4：更新得出当前最优解，判断适应度函数值是否达到精度要求，满足则生成最优解，否则继续执行Step3～Step4。

Step5：达到最大迭代次数或适应度函数值满足精度要求，则将输出的结果作为最优的权值、阈值参数组合。

Step6：利用优化后的Elman神经网络，对各模态分量进行滚动预测。

3 预测模型构建

发电厂发电量影响因素很多，比如天气、湿度、煤耗等等［9］，在进行发电量预测时，如果要将所有可能的影响因素都从原始数据中拆分出来并逐一比较其相关系数，难度会非常大。而且，由于静态相关系数排序是固定的，对于实时变化的发电量预测精度可能会不够。

目前很多时间序列预测研究都采用了分解算法对数据进行处理，经验模态分解（Empirical Mode Decomposition，EMD）作为基础分解算法，能够将原始负荷数据分解为平稳序列和非平稳序列［28］，在研究中得到了广泛应用。然而，EMD方法容易出现模态混叠现象，从而在预测时产生不利的影响。为解决这一问题，文献［29］提出一种基于变分模态分解的方法，能够将负荷数据分解为特征互异的IMF，减缓出现模态混叠的现象，方便进一步分析数据。

为了避免对发电量影响因素的分析并充分利用数据本身的规律，本文采用滚动预测的思想，用数据自身的关联度来代替影响发电量的因素数据，极大地利用原始数据本身的特性，并使用VMD对原始数据进行分解处理。主要思路为：将原始电厂发电量数据集分解为不同的模态分量，并根据特征重新组合，以滚动数据集的形式输入建立好的BAS-Elman 预测模型，分别对重组后的模态进行预测，最后将各部分预测结果综合，以获得更平滑且具有明显特征的预测结果。具体预测流程如图3所示。

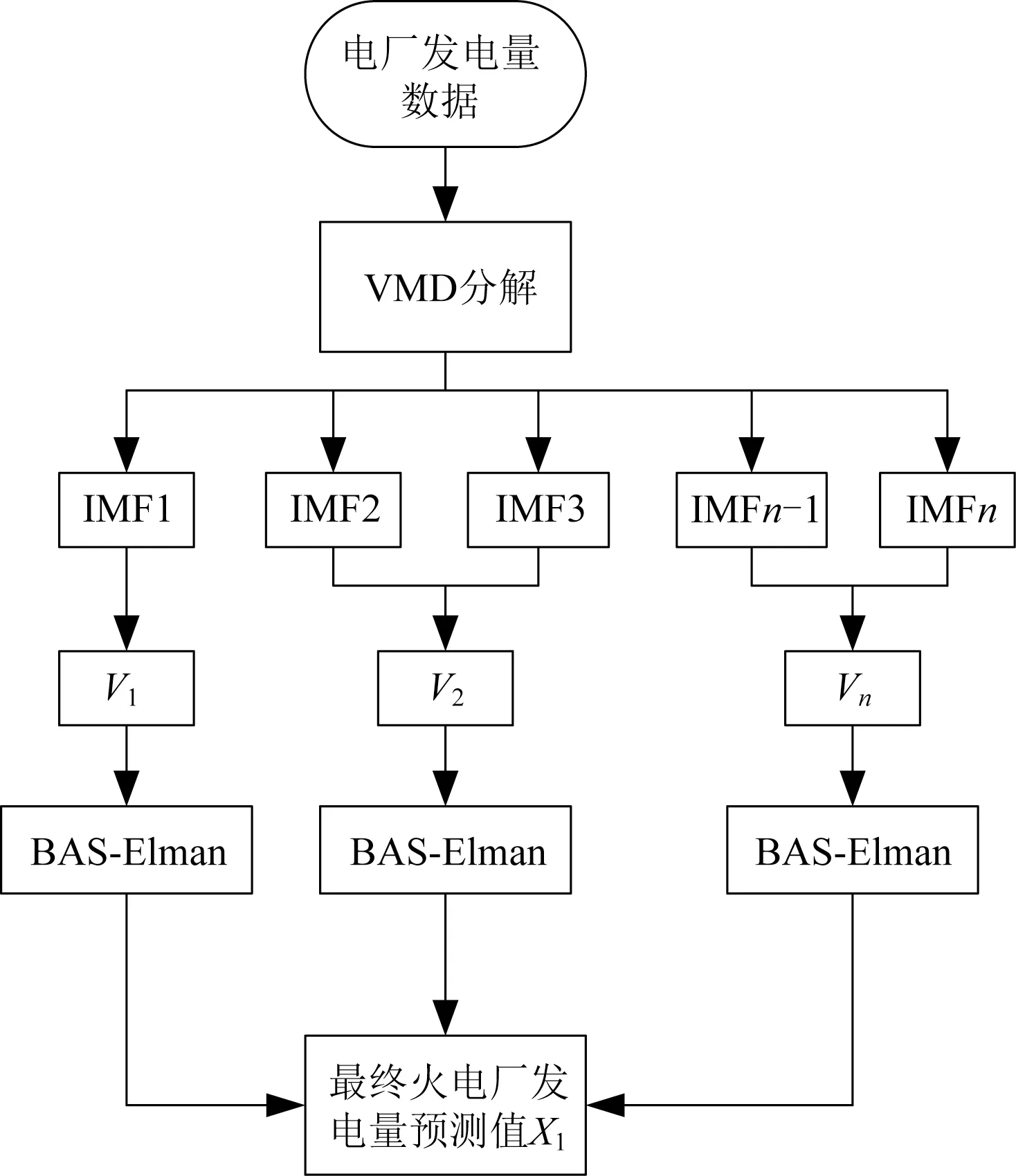
图3 BAS-Elman发电厂发电量预测流程图Fig.3 Flow chart of power plant generation forecast by BAS-Elman

Elman 神经网络的结构比较灵活，可以根据具体任务和数据的特点来调整网络的结构和参数，这使得它能够适应不同的数据和任务需求。Elman神经网络可以通过反向传播算法进行训练，使得网络能够自适应地学习数据的特征和规律，这样可以提高网络的预测精度和鲁棒性。

为更好适应该模型，所有数据在输入BAS-Elman模型前，均进行数据归一化处理。

4 计算结果及分析

4.1 样本数据

上海某发电厂2016 年—2022 年的月度发电量如表1所示。

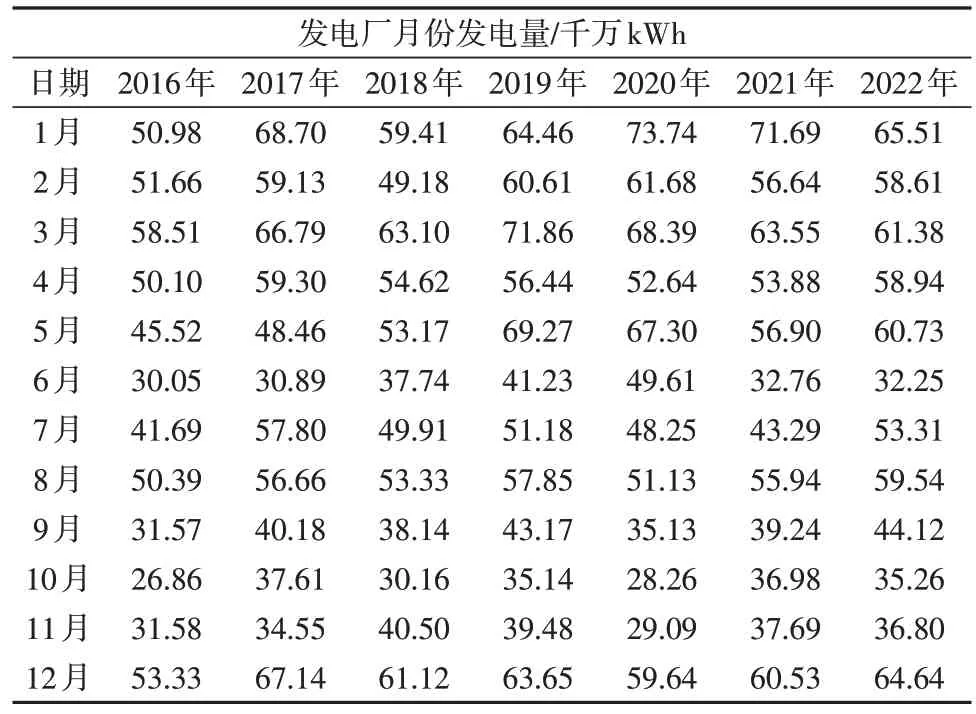
表1 上海某发电厂2016年-2022年发电量Table 1 Power generation of a power plant in Shanghai from 2016 to 2022

从表1中可以看出发电厂发电量具有数据量小和非平稳的特点。

为了充分利用原始数据特征且扩大原始数据量，使用一种可更新的滚动预测方法，具体为：在每个重构后的模块中，利用前6个月数据作为一组输入，预测第7个月的数据，将接下来的6个月数据作为输入的第二组数据，如此反复，不断进行下去，形成滚动数据集。具体的数据构建方式如表2所示。

表2 发电厂发电量滚动数据集Table 2 Rolling data set of power plant generation

表1 中有2016 年-2022 年共84 个月的发电量数据，依照表2规律可以组成78组滚动数据集。具体仿真时，将2016 年1 月至2021 年12 月滚动形成的66 组数据作为训练集，2022 年12 个月输出的12 组数据作为验证集，进行对照检验。

4.2 网络参数设置

1） VMD模态分解。

发电量数据具有随机性和波动性，本文采用VMD对原始数据进行分解，分解结果如图4 所示。利用中心频率法确定分解层数K=5。其余参数设置：起始中心频率ω=0，惩罚因子α=2 000；收敛判据ε=10-7。

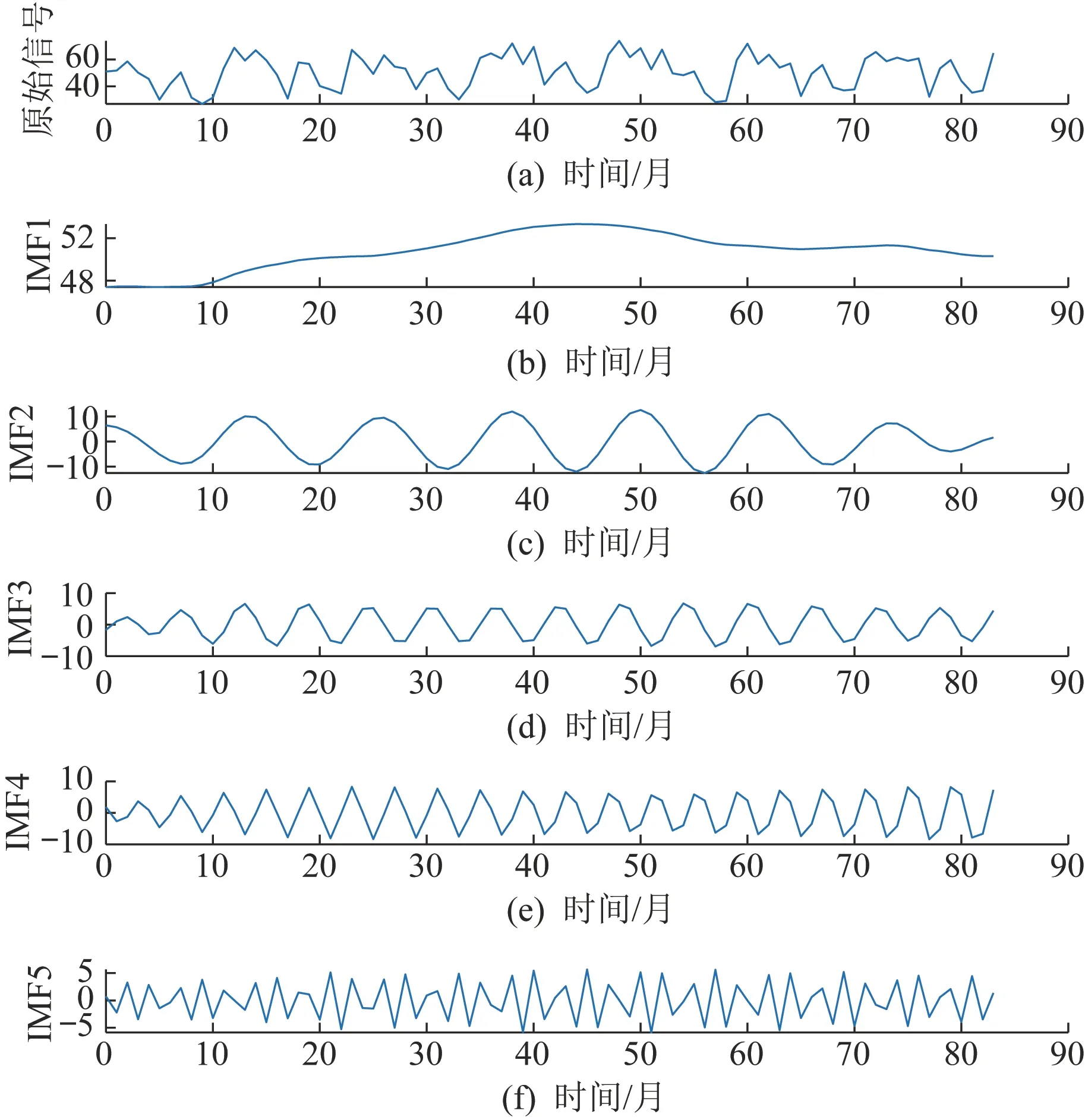
图4 VMD分解模态分量Fig.4 VMD decomposition modal components

根据以上分解结果可以看出，IMF1 幅值与其他4 个模态相距较大，可单独构成V1，IMF2、IMF3 和IMF4幅值接近且较为平滑，可组合构成V2，IMF5噪声较大且幅值较小，可单独构成V3。重构后的模块可分别看成发电厂发电量包含的趋势性、周期性和随机性。

重构后的模态分量图如图5所示。

图5 重构后的模态分量Fig.5 Modal components after reconstruction

2） Elman网络参数设置。

使用MATLAB 平台进行BAS- Elman 预测模型仿真，对于Elman神经网络，根据分解出的分量模态数据特点，确定模型隐层节点的个数，为了使数据和算法更加适应，确定Elman 神经网络结构输入层6个神经元，隐含层6 个神经元，输出层1 个神经元［30-33］，天牛须搜索算法的空间维度取值为75，步长因子ζ取值为15，迭代次数n取值为150。

4.3 评价标准

为了评估模型的效果，使用均方根误差、平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）和平均绝对误差（Mean Absolute Percentage Error，MAE）作为模型评价指标。表达式如下：

式（12）-式（14）中，yi为实际值；ŷi为预测值；m为预测样本数。

4.4 预测结果及比较

1） 分量预测结果

重构后的分量V1、V2、V3 的预测结果分别如图6～图8所示。

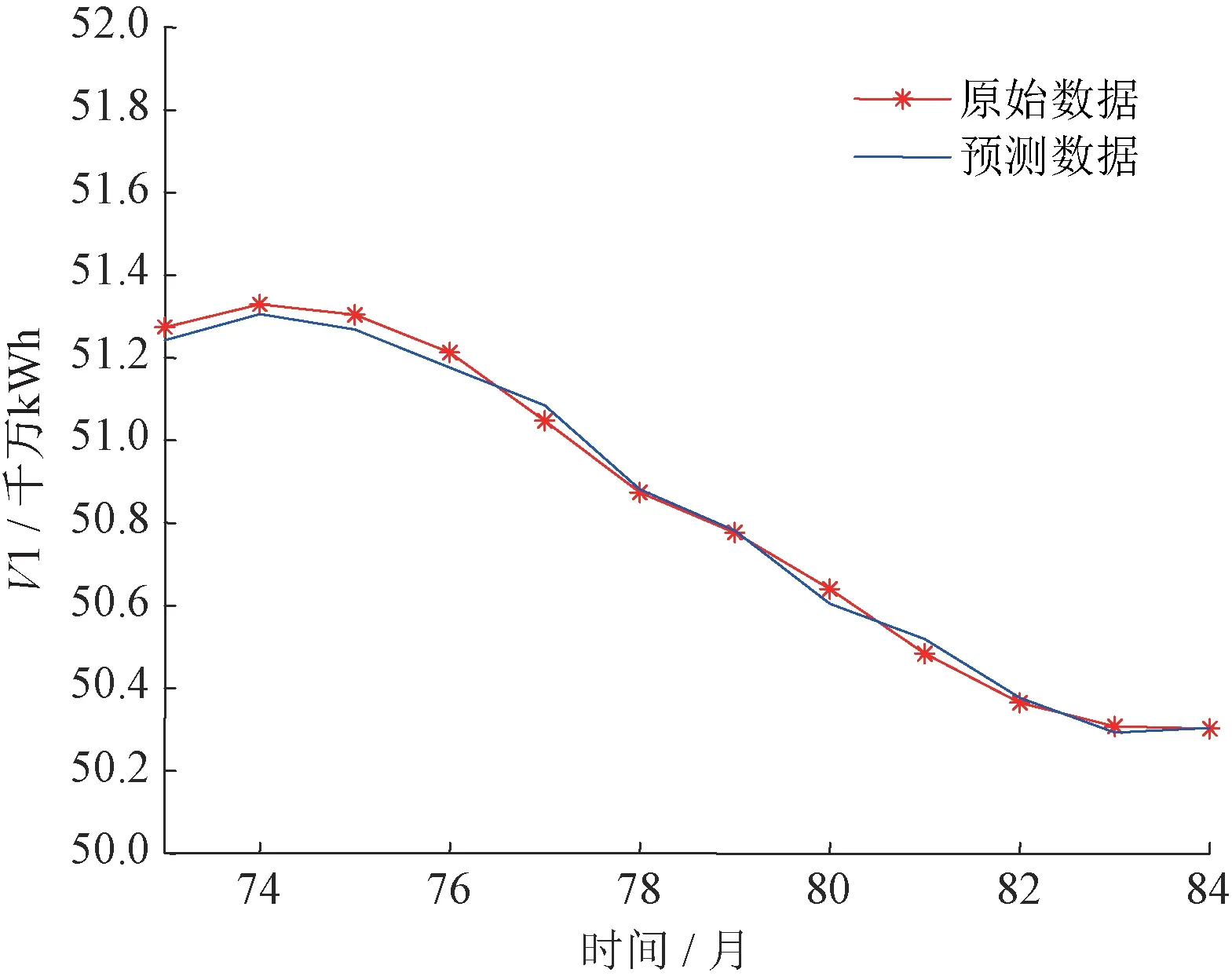
图6 重构分量V1预测结果Fig.6 Prediction results of reconstructed component V1

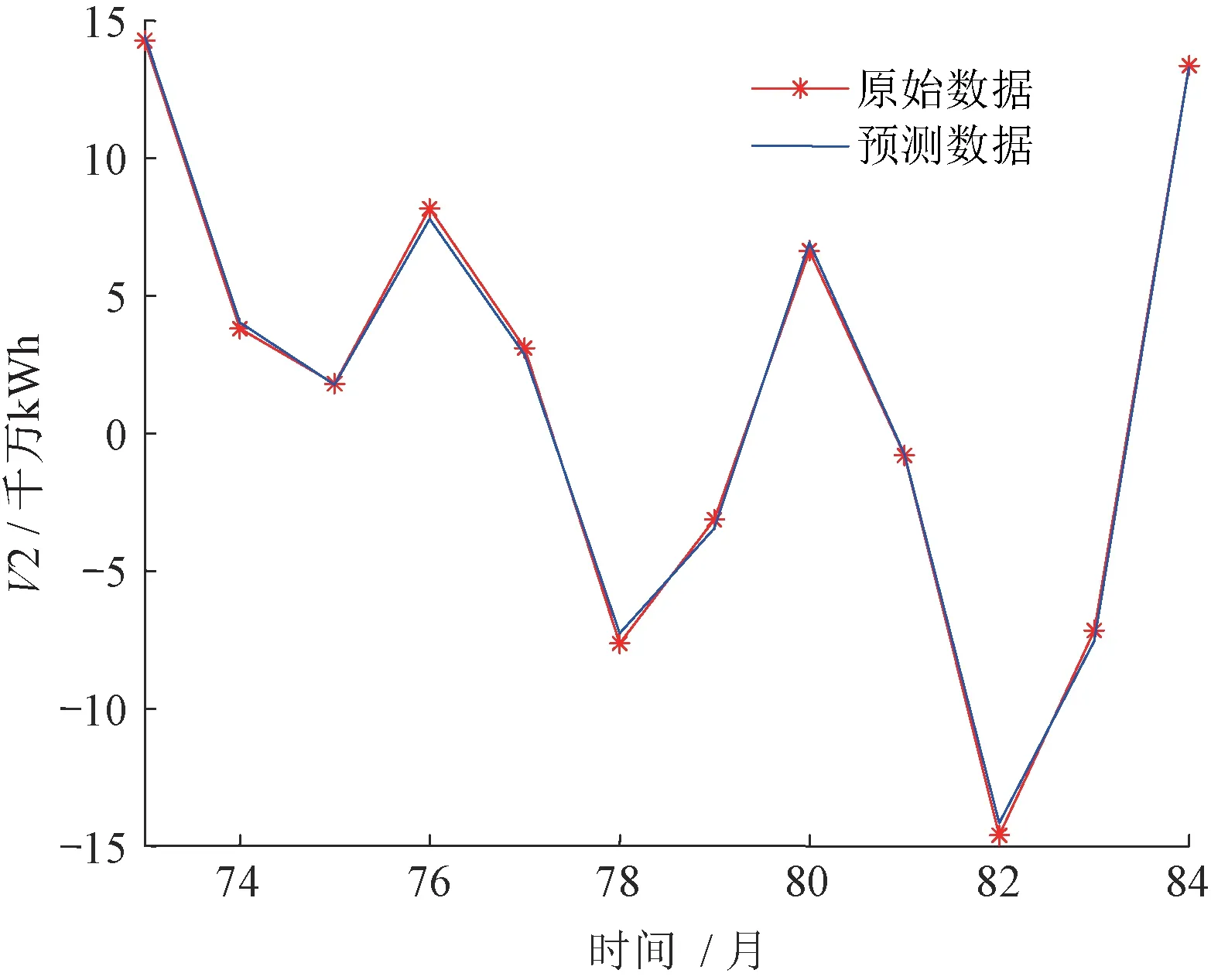
图7 重构分量V2预测结果Fig.7 Prediction results of reconstructed component V2

图8 重构分量V3预测结果Fig.8 Prediction results of reconstructed component V3

2） 最终预测结果

将重构分量的预测结果相加，得到最终的预测结果如图9所示。

图9 最终预测结果Fig.9 Final forecast results

将VMD-BAS-Elman 的预测效果与未优化的Elman神经网络和没有分解直接预测的BAS-Elman模型的预测结果进行对比，结果如图10所示。

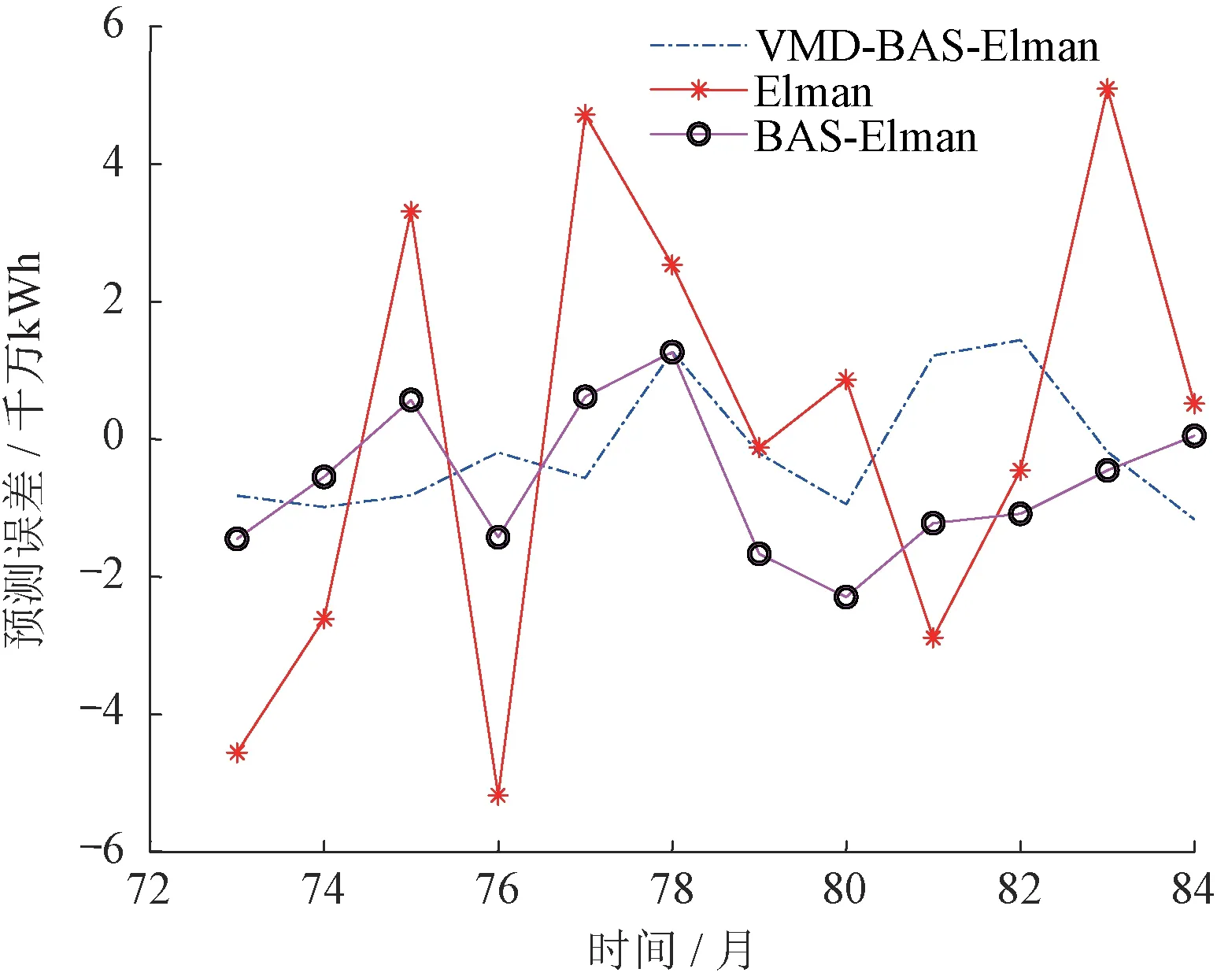
图10 预测结果误差对比图Fig.10 Comparison chart of prediction result error

图10中3种算法的误差指标如表3所示。

表3 各预测模型的误差评价指标Table 3 Error evaluation indicators of each prediction model

5 结语

本文针对发电厂发电量预测精度不高的问题，提出了一种VMD-BAS-Elman 中长期发电厂发电量预测模型，通过实例研究，得出以下结论：

1） 本文采用变分模态分解技术对发电厂历史发电量进行分解，VMD技术可以将原始序列分解为多个具有不同特征的模态，通过分别预测每个模态，更好地利用数据本身的特征得到预测结果。同时，VMD技术可以将相邻的模态整合重构，减小了预测过程的计算量，使得预测结果更加快速和精准。此外，使用VMD技术可以降低原始序列非平稳性的特点，有助于提高预测模型的性能和稳定性。

2） 针对发电厂发电量数据量不足的问题，使用滚动输入的方法，扩充原本数据量的同时，可以更好地利用数据本身的特征，避免了发电量数据影响因素分析难的问题，也不会因为影响因素筛选过多或过少对预测结果产生影响。

3） 结合历史数据建立基于VMD-BAS-Elman的发电量滚动预测模型，由于Elman 神经网络初始权值和阈值具有随机性，为了减小这种随机性对发电厂发电量预测模型最后精确度的影响，引入BAS 算法进行改进，提高了Elman神经网络的运行速度，同时使模型更加容易找到全局最优解。与单一的Elman模型和未进行分解的预测模型相比，实验结果表明，基于VMDBAS-Elman的发电厂发电量预测模型具有更高的精度和更好的实用性，能够更好地支持火电企业的决策分析。

综上所述，本文的研究成果为火电企业提供了一种有效的发电量预测方法，有望在实际应用中发挥重要作用，为企业决策提供有力支持。