水库石料场终采边坡方案研究
2023-09-12韩新捷孙志翔徐梦佳俞正浩
韩新捷,孙志翔,徐梦佳,俞正浩
(浙江省水利水电勘测设计院有限责任公司,浙江 杭州 310000)
针对水电、水利工程料场高边坡具有高度大、坡度陡、卸荷速度快等特点,赵建军[1]提出了边坡稳定性动态评价,指导支护设计的方法;张显书[2]利用数值仿真,对不同开挖角的高边坡稳定性和变形进行计算,综合技术经济比较,确定了边坡结构处理的最优方案;陈星[3]通过三维数值模拟对4种开挖方案的位移、应力、塑性区、安全系数、开挖方量、开采难易程度进行综合比较分析,为选择最优方案提供了思路。
本文通过嵊州市某拟建水利枢纽工程的2#料场边坡,模拟研究不同坡比、马道宽度、马道级差对料场有用层开采量和边坡安全系数的影响,探求既定开挖顶底高程条件下,料场的最优开采方案。综合考虑边坡稳定和经济性,精确计算有用层开采量,选择最优开挖方案,对实际工程施工具有一定的指导意义。
1 开采方案设计
1.1 工程概况
绍兴地区主要山脉为会稽山,其主要地层岩性为白垩系下统的火山碎屑,为地区的工程建设提供了良好的天然石料场。在水库区内经比选确定的料场岩性稳定,地质构造不发育,地质条件较简单,天然建材开挖主要受征地红线限制。如何在既定范围内一方面保证边坡稳定,减少支护投入,同时尽可能增加有用层开挖量,保证天然建材供应,增加有效库容,成为石料场开挖方案设计的主要考虑方向。
嵊州市某拟建水利枢纽工程的2#料场位于规划堆石坝上游右岸,计划开采石料430万m3。2#石料场在大坝填筑期同步开挖,一方面提供堆石坝所需填筑料和混凝土骨料,另一方面可增大拟建水库库容,水库建设完成后将形成终采边坡。2#料场现状地形如图1所示。

图1 2#料场平面图
根据地质勘察成果,2#料场边坡坡表为第四系全新统残坡积(el-dlQ4)含碎石粉质粘土,厚度0.3~2.0m不等,基岩为白垩系下统西山头组上段(K1x2)熔结凝灰岩,强风化带厚0.5~1.2m,弱风化带厚5.0~10.0m,其下为微风化至新鲜,绘制H8-H8’地质剖面图如图2所示。

图2 2#料场工程地质剖面图
1.2 方案设计
根据SL 386—2007《水利水电工程边坡设计规范》可确定2#料场边坡级别为2级,对应的抗滑稳定安全系数为1.25~1.20。
该石料场初步考虑开挖至高程200m,河床高程约80m,开挖后将形成高差约120m的终采边坡。根据规范,结合工程实际,弱-微风化岩质边坡坡比可达到1∶0.3,设置马道宽度不宜小于2.0m,马道高差不宜大于20m。
根据以上情况,设计不同的料场边坡开挖方案。考虑边坡坡比、马道高差和马道宽度3个因素,每个因素4个水平,设计坡比依次为1.0∶0.3、1.0∶0.4、1.0∶0.5、1.0∶0.6,单级马道宽度依次为2.0、2.5、3.0、3.5m,各级马道高差依次为10、12、15、20m。3种因素组合共计形成64个开挖方案。
不同开挖路径对应不同的终采边坡坡面形态,同样的地质条件下,边坡稳定系数应符合坡比越小、安全系数越大这一规律。但是随着坡比变小,终采边坡形态变缓,有用层开采量随之减小,两者存在矛盾统一的关系。因此,安全系数满足要求条件下,实现有用层开采量最大化的方案,即为料场边坡开采的最优方案。边坡典型开挖方案如图3所示。

图3 典型开挖方案示意图
图示方案a为最陡开采方案,方案b为最缓开采方案,根据方案设计,a和b之间存在其余62组开采方案。不难发现,安全系数(Fs)和有用层开采量(R)保持着如下关系:Fsa为所有方案的最小值,Fsb为所有方案的最大值;Ra为所有方案的最大值,Rb为所有方案的最小值。
其中存在着同时满足边坡安全系数和有用层开采量,且能实现效益最大化的方案,即为该料场边坡开采的最优方案。
2 方案分析
2.1 原始边坡的稳定性计算
利用极限平衡法计算2#料场边坡现阶段的稳定性情况,根据熔结凝灰岩的抗剪强度参数(见表1),分别计算发生整体破坏和局部破坏的安全系数,计算结果如图4—5。
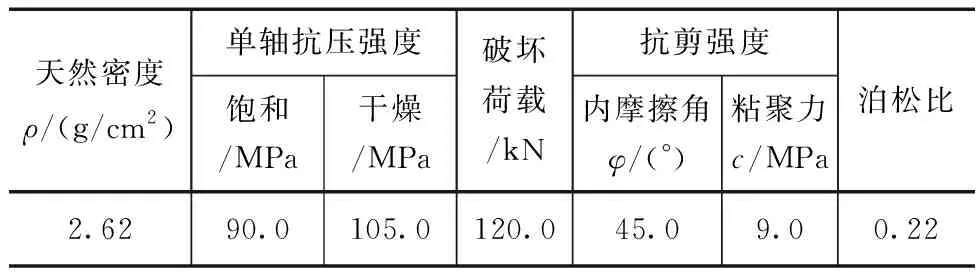
表1 岩体物理力学参数
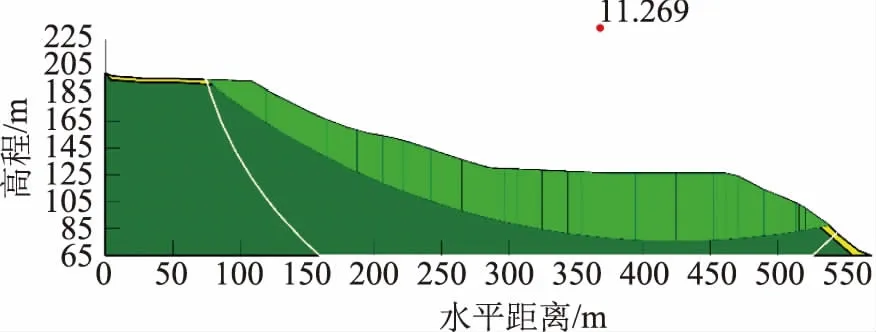
图4 现状边坡整体破坏稳定性计算

图5 现状边坡局部破坏稳定性计算
根据现状边坡的稳定性计算结果可知,边坡整体破坏的安全系数为11.266,局部破坏的安全系数为7.501,该边坡现状处于稳定状态。
2.2 不同开采方案边坡稳定性计算
2#料场边坡开挖顶高程200m,底高程80m,选取同一典型剖面,对不同开采方案分别计算终采边坡安全系数。部分方案安全系数计算结果如图6所示。

图6 不同方案的稳定性计算结果(部分)
2.3 不同开采方案边坡有用层开采量计算
建立2#料场的三维地质模型,利用河床做为开挖基底,后缘先建立垂直面,顶高程为200m,坡表残坡积层和强风化岩为剥离层,平均厚度约3.2m,建立的三维地质模型如图7所示。

图7 2#料场边坡三维地质模型
通过计算分析可知:垂直开挖条件下,剥离层方量为47.20万m3,有用层开采量为560.22万m3,此时的剥采比最小,为1∶11.9;在不同开采方案下,无用层开挖量几乎不变,有用层开采量发生变化,剥采比也随之改变。
2.4 计算结果及分析
通过对64个不同开采方案的模拟计算,其安全系数和有用层开采量计算结果见表2。

表2 不同方案开采方量与边坡稳定性计算结果
根据工程建设需求,开采方案需同时满足终采边坡安全系数不小于1.20,有用层开采量不小于430万m3。据此绘制不同方案的安全系数和有用层开采量折线图(如图8所示),可知同时满足安全系数和有用层开采量两个条件的方案共有方案17、方案21、方案23、方案24、方案25、方案26、方案27、方案31、方案32、方案45,共计9组方案。
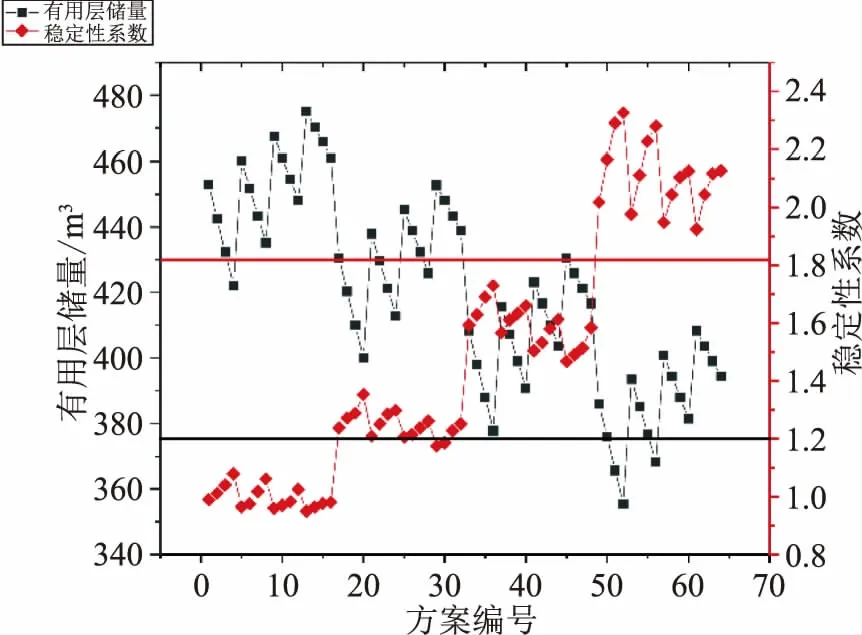
图8 不同方案的计算结果
其中方案25(坡比1∶0.4、马道高差15m、马道宽度2.0m)的安全系数最小,为1.206,其对应的有用层开采量为445.3万m3,方案45(坡比1∶0.5、马道高差20m、马道宽度2.0m)的安全系数最大,为1.467,其对应的有用层开采量为430.47万m3,方案17(坡比1∶0.4、马道高差10m、马道宽度2.0m)与方案45两者的有用层开采量接近,安全系数仅为1.238。
在满足安全系数1.20时,方案25可多开采15.3万m3石料;在满足开采量430万m3时,方案45可建立安全系数为1.467的终采边坡。有用层开采量整体随着安全系数的增大而减小。
3 基于正交试验的参数敏感性分析
3.1 正交试验原理
正交试验是一种基于数理统计方法来分析多因素影响规律的试验设计方法,可以用来表征不同因素对试验指标作用的主次顺序[5],本文利用正交试验分析料场终采边坡的坡比、马道高差、马道宽度3个因素对于边坡安全系数和有用层开采量的影响规律及大小。
首先根据工程实际和经验分析制定合适的正交表Ln(tm),其中L为正交表符号;n为正交表的行数;t为各个因素的水平个数;m为正交表列数,即为因素个数。然后按照正交表填入对应的安全系数和有用层开采量计算结果[6]。本文选用方差分析来进行3个参数的敏感性分析,用各个参数的变差平方和除以误差平方和构造出F检验的统计量,进行F检验,根据检验结果判断3个参数对安全系数和有用层开采量影响的显著程度。
3.2 正交试验及结果分析
选取坡比、马道高差、马道宽度做为试验因素,每个因素有4个水平,见表3。
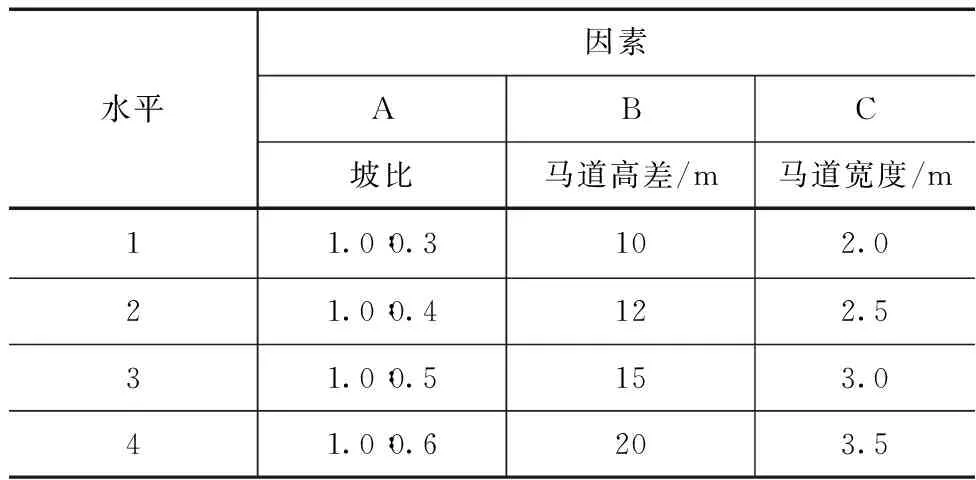
表3 因素水平表
根据终采边坡设计方案确定的3因素4水平,采用L16(45)正交表设计试验方案,分别建立16组不同参数条件的计算模型,其安全系数和有用层开采量计算结果见表4。其中第4列、第5列为空列,即误差列。

表4 正交试验方案及其结果
利用公式计算出各因素的变差平方和Sj,在正交试验表中第4列、第5列即D、E参数为无因素列,称为误差列,其Se=S4+S5,相对应自由度为fe=f6+f7,对应的安全系数方差分析表见表5,有用层开采量方差分析表见表6。根据F检验临界值表可确定,若因素F检验的统计量Fj大于F0.01(3,3)=29.457,则称该因素为高度显著;若因素F检验的统计量Fj小于F0.05(3,3)=9.277,则称该因素为不显著;若因素F检验的统计量Fj处于两者之间则称该因素为显著。各因素的安全系数方差分析表见表5,有用层开采量方差分析表见表6。

表5 安全系数方差分析表

表6 有用层开采量方差分析表
根据分析结果可知,坡比对边坡安全系数和有用层开采量的影响优先级均高于其他两因素,对于安全系数的正面影响要显著于对有用层开采量的负面影响。在同时满足安全系数和有用层开采量两个条件的9组方案中,方案45终采边坡坡面更缓,马道级数少仅有5级,且单级马道宽度最窄为2.0m,可以判定为该料场边坡的最优开采方案。
4 最优开采方案的边坡有限元分析
在确定最优路径终采边坡后,进一步分析其三维应力及应变问题[4]。
建立方案45(坡比1∶0.5、马道高差20m、马道宽度2.0m)的三维有限元计算模型,同时给模型赋予取得的地质材料强度参数,使其在自重条件下稳定,消除自重产生的竖向位移增量,模拟现阶段边坡的稳定性状态。建立的三维有限元模型如图9所示,三维网格模型如图10所示。

图9 三维有限元计算模型

图10 三维有限元模型网格剖分
根据边坡的开采方案,建立后缘边坡,使之切割原始边坡模型,将三维有限元模型分为开挖体和终采边坡两部分。利用ABAQUS软件自带的生死单元功能,将初始模型按照开挖顺序逐级移除直至80m河床高程处,分别计算该开挖方案下的边坡塑性区分布,最大主应力、最小主应力分布,各方向位移分布,其计算结果如图11—13。

图11 开挖后塑性区分布
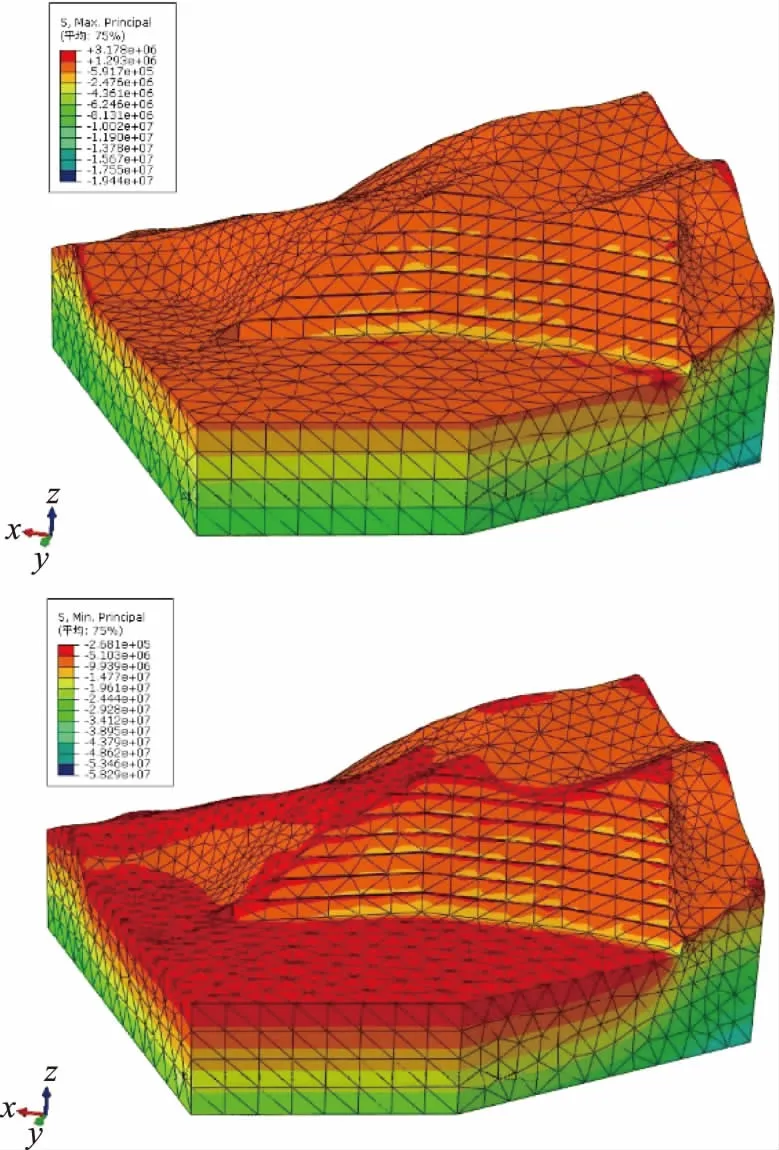
图12 开挖后应力分布云图

图13 开挖后应变分布云图
根据三维有限元计算结果得到的塑性区分布图可知,方案45未出现塑性区贯通现象,与二位极限平衡稳定性取值相符合。该方案塑性区仅在第一级马道,即100m高程处出露,该部位可能发生小范围剪切破坏,可进行局部支护加固。根据应力分布云图可知,方案45应力集中现象不明显,仅在各级马道位置发生最小主应力集中,其特征值为5.103MPa。根据应变分布云图可知,方案45的x方向位移集中在左侧山体,即实际边坡的下游侧山体向边坡临空面方向发生变形,y方向位移集中在右侧,即终采边坡后缘区域,向临空面方向突出,x向最大位移值为0.058m,y向最大位移值为0.251m,可对后缘边坡中下部采用锚杆适当支护防止发生边坡变形破坏。
根据方案45的三维有限元计算结果可知,该方案终采边坡在塑性区、应力、应变方面均满足边坡稳定要求,开挖方量满足大坝填筑需求,且开挖后形成的终采边坡安全系数为1.467,为该料场边坡的最优开采方案。
5 结论
本文通过嵊州市某拟建水利枢纽工程2#料场边坡实例,研究不同开采方案的安全系数和有用层开采量,探寻最优开采方案。
(1)通过设定不同的坡比、马道高差和马道宽度,进行全面试验,计算不同方案的安全系数和有用层开采量,共有9组试验同时满足稳定性和方量需求;
(2)利用正交试验分析参数敏感性可知,坡比相较于马道高差和马道宽度,对安全系数和有用层开采量的影响均更显著,且对安全系数的正向影响高于对有用层方量的负面影响,因此判断方案45为最优开采方案;
(3)通过对最优方案45的三维有限元模拟,可知其在塑性区分布、应力分布、应变分布均满足要求。
