弧后C4F7N/N2混合气体复原过程研究

庚振新,张 孟,张 佳,夏亚龙,林 莘,刘祥峰

(1.沈阳工业大学, 辽宁 沈阳 110870;2.国网甘肃省电力公司电力科学研究院,甘肃 兰州 730070;3.国网四川省电力公司电力科学研究院,四川 成都 610041)

0 引 言

C4F7N气体具有优良的绝缘性能和环保特性,是目前潜在替代SF6的绝缘介质之一[1-3]。由于C4F7N液化温度较高[4],一般需与缓冲气体混合使用。

近几年国内外学者对C4F7N及其混合气体的分解机理展开了研究,文献[5-8]对C4F7N混合气体的热力学参数进行了研究,计算了不同比例下的定压比热、饱和蒸汽压、质量密度等参数。文献[9-11]对C4F7N/N2混合气体的分解机理进行了研究,通过建模计算了不同温度下C4F7N和N2的分解情况。研究发现N2作为缓冲气体,在高能电场或局部过热的条件下,避免了C4F7N的大量分解。文献[12-15]研究了C4F7N/N2混合气体的部分分解路径,结合过渡态理论,计算了分解反应的速率常数。近些年国内外学者对绝缘气体的分解体系研究逐渐完善,但对于绝缘气体的复原过程却鲜有报道。

考虑到液化温度、绝缘强度等因素的影响,下面在C4F7N/N2混合气体局部热力学平衡计算的基础上,开展弧后C4F7N/N2混合气体的复原过程研究。首先,确立C4F7N/N2混合气体的反应粒子种类,计算出热力学平衡状态下0.3～30 kK温度范围内的粒子浓度;然后,确定C4F7N/N2混合气体反应路径并计算各反应的反应速率常数,引用0.1 MPa下C4F7N/N2混合气体弧后的温度衰减曲线作为模拟弧后C4F7N/N2混合气体复原过程中的温度变化数据,通过ANSYS软件计算弧后C4F7N/N2混合气体粒子复原过程的摩尔分数变化;最后,与热力学平衡状态的粒子摩尔分数进行对比与分析并进行总结。

1 反应粒子种类

首先,考虑C4F7N/N2混合气体可能生成的粒子种类,并对粒子进行几何结构优化及能量的计算,这是计算热力学平衡条件下粒子浓度变化和弧后混合气体复合过程的第一步。C4F7N/N2混合气体可能生成的粒子共52种,如表1所示。

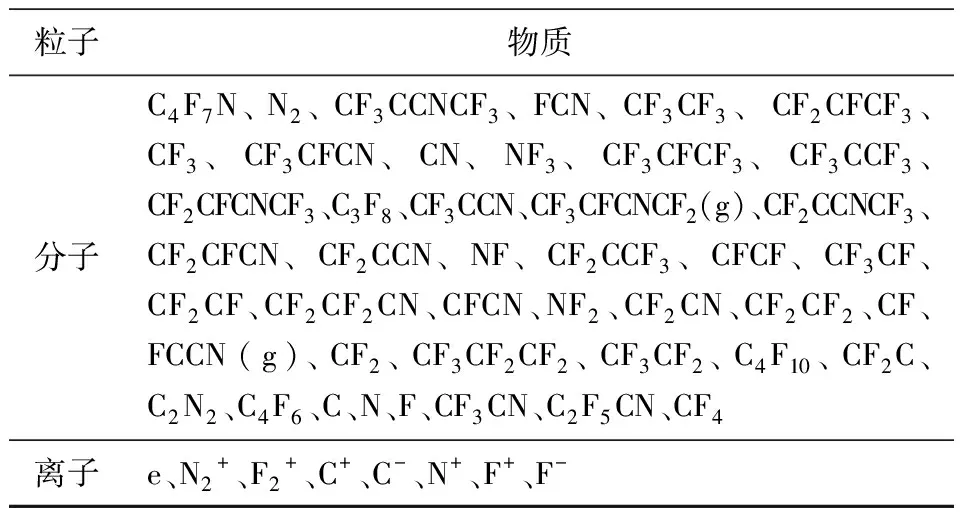
表1 C4F7N/N2生成粒子种类

通过仿真软件构建52种粒子的分子模型,用B3LYP密度泛函的方法在6-311+G(d,p) 基组水平上对分子进行结构优化。在得到最优分子几何结构的基础上,采用更高水平的CCSD(T)/def2-TZVPP方法计算最优分子结构的最低能量以及熵、焓等参数。

2 热平衡状态下粒子浓度计算

为了研究弧后C4F7N/N2混合气体复原过程,先计算了热力学平衡状态下混合气体的分解情况。假设局部热力学平衡(local ermodynamic equilibrium,LTE),用牛顿-拉夫森算法[16]将等离子体系统的吉布斯自由能降至最小,模拟在0.3～30 kK温度范围内0.1 MPa下9%C4F7N与91%N2混合气体分解后各粒子的摩尔分数,如图1所示。

图1 热力学平衡状态下粒子浓度变化

图1(a)中可以看出:C4F7N分子在0.5～0.7 kK温度下就开始分解,在不到3 kK的温度下,基本上已经分解殆尽,与文献[17]计算结果基本一致;而N2在3 kK的温度下开始分解,在6 kK左右开始大量分解,与文献[18]结果基本一致;在0.3～3 kK温度范围内,C4F7N/N2混合气体的粒子组分主要由C2F5CN、C4F10、CF3CN、CF3、CFN等组成。

C4F7N分解过程中,C4F10、C2F5CN、CF3CN等粒子最早出现,随着温度继续升高,生成的粒子继续发生分解,在温度达到30 kK时的粒子基本为小分子粒子及带电粒子,如N+、C+、N+、C、N等自由基粒子,如图1(b)所示。

3 反应路径与速率常数

确定反应路径并计算其正向速率常数和逆向速率常数是研究弧后C4F7N/N2混合气体复原过程的关键步骤。下面根据C4F7N和N2的分子结构,确立了C4F7N/N2混合气体可能发生的67种反应路径及生成粒子种类后,计算各反应的速率常数。

对于有过渡态的反应,采用过渡态理论(transient-state theory,TST)计算反应速率常数[19]。以反应式CF3+CF3CFCN→CF4+CF2CFCN为例,当C1与F2的化学键发生断裂且F2与C9产生化学键的过程中,扫描出反应中存在过渡态,如图2所示。

图2 过渡态分子结构

将过渡态按照粒子的计算方式进行结构优化和高基组的能量计算。将Gaussian软件中结构优化后的过渡态及生成物CF4和CF2CFCN的输出文件进行能量校正后,将输出文件放入kisthelp软件中。通过设置温度,可以计算出该温度下过渡态到生成物的速率常数。设置的温度范围为0.3～30 kK,温度间隔0.1 kK。计算特定温度下的正向速率常数的公式为

(1)

式中:T为温度;kTST(T)为正向速率常数;kb为玻尔兹曼常数;P0为标准大气压(0.1 MPa);h为普朗克常数;R为理想气体常数;ΔG0,≠为反应的标准吉布斯自由能;Δn表示气相双分子反应为1或单分子反应为0;κ为振动的缩放系数;σ为反应路径简并度[15]。反应的平衡常数Kc可由式(2)得到。

(2)

式中,ΔS0和ΔH0分别为反应中从反应物CF3和CF3CFCN到生成物CF4和CF2CFCN完全转变过程中发生的熵变和焓变;Δλ为某一组分从反应物到过渡态过程中净化学计量系数的改变量,反应物为单原子反应时,Δλ=0,反应物为双原子反应时,Δλ=-1,这里计算多数采用单原子反应。

用正向速率常数kTST(T)除于平衡常数Kc,可得到逆向速率常数kf。计算出该反应不同温度下的逆向速率常数后,将逆向速率常数拟合为kf(T)

kf(T)=ATnexp(-Ea/RT)

(3)

式中:A为前因子;n为温度指数;Ea为反应活化能。用这3个参数可以确定不同温度下的逆向反应速率常数,正向速率常数也用此方法进行拟合。

对于反应式中没有过渡态的反应即无势垒反应,采用变分过渡态理论(variational transient-state theory,VTST)的方法计算反应速率。通过Gaussian软件将反应中反应物断裂的化学键设置为柔性扫描,步长为0.1 A,设置50步柔性扫描。反应物的化学键从连接到断裂分解为生成物的过程中,每一步长的变化都可以获得该状态下的分子结构。将每步长下的分子结构进行相同方法的结构优化及高基组的单点能计算,通过上述计算过渡态与生成物的反应速率常数的方法,可得到该步长下不同温度的速率常数。

根据VTST理论,一个温度下反应的速率常数应为不同步长计算的速率常数的最小值,所以应当筛选所有计算的温度中该温度下不同步长的速率常数的最小值。将不同温度下的速率常数最小值按照式(2)的方法拟合,可获得无势垒反应的3个反应速率常数A、n、Ea。

4 弧后温度设定

为了模拟弧后C4F7N/N2混合气体的复原情况,引用0.1 MPa下C4F7N/N2混合气体电流过零后的电弧温度衰减曲线[20-21],如图3所示,将此温度作为C4F7N/N2混合气体复原时的仿真温度。将弧后温度衰减曲线分为3个阶段:第一阶段为0～0.05 ms内的快速衰减区,温度从17 kK迅速衰减到8 kK左右;第二阶段为0.05～1.00 ms的缓慢衰减区,温度从8 kK逐渐衰减到3 kK左右;第三阶段为1.00～6.00 ms的平稳衰减期,温度从3 kK逐渐降低至2 kK左右。

图3 弧后温度与时间关系

在确定反应路径及速率常数、反应产物和弧后温度变化的基础上,通过Chemkin软件设定反应体系的初始混合比为9%C4F7N与91%N2、压力为0.1 MPa等参数,最后可求得C4F7N/N2混合气体反应后各粒子摩尔分数随时间的变化曲线。

5 结果与分析

模拟C4F7N/N2混合气体弧后的复原过程,计算求得混合气体的粒子如图4所示。C4F7N/N2混合气体在弧后的第一阶段10-8ms内就已完全分解为CF3CFCF3、CF3CCF3、CF3CCN、CF2CFCN、CF2CCN等大分子粒子;大分子粒子在10 kK以上的高温下也很难稳定存在,最终以C、N、F、CFCF、CF2C等粒子和自由基的形式存在。C、N、F等原子在更高温度下会变成带电粒子,如C+、N+、F-等,由于模拟C4F7N/N2混合气体弧后的复原过程中未能考虑电离反应,因此在弧后温度8 kK以上时基本只有C、N、F粒子存在。

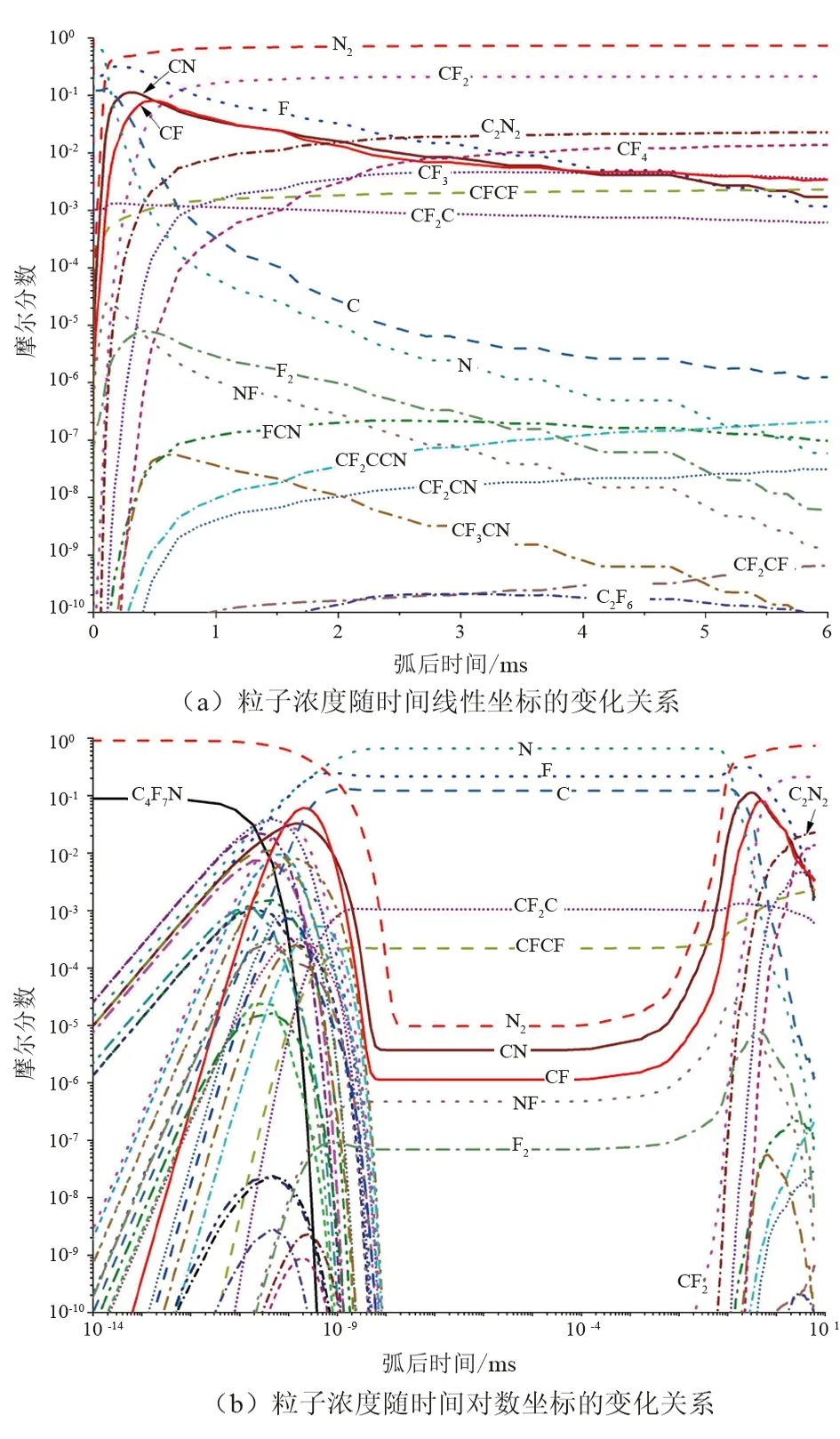
图4 混合气体粒子浓度变化

随着弧后温度逐渐降低,在弧后的第二阶段约8 kK时粒子开始复合,N2、CF、CN等粒子迅速大量复合至摩尔分数10%以上,CF2、C2N2、CF3、CF4等粒子也随之开始复合,而C、N、F粒子的摩尔分数开始下降。

在弧后的第三阶段即2～3 kK时,N2大量复原至摩尔分数70%以上;CF2、C2N2、CF4等粒子大量复合至摩尔分数1%以上。由于CF2粒子主要由CF和F复合生成;C2N2主要由CN复合生成;CF3、CF4粒子主要由F、CF、CF2粒子的复合生成:因此CF、CN等粒子的摩尔分数开始下降,C、N、F粒子的摩尔分数下降至10-6以下。

通过对图4中C4F7N/N2混合气体的复合结果进行分析,N2、C2N2、CF2等粒子相比于CF、CN、NF等粒子更加稳定,而CF、CN、NF等粒子又比C、N、F粒子稳定。文献[13-14]通过实验检测C4F7N/N2混合气体分解后的产物主要有N2、CF3、CF4、C2N2等粒子,模拟弧后C4F7N/N2混合气体复原过程的产物与实验结果基本一致。除此之外,图4中还有FCN、CF2CCN、CF2CN、CF2CF等粒子的复合,而由于这些粒子的摩尔分数低于10-6,因此在实际检测中由于摩尔分数太低而未被检测到。

6 结 论

通过确立C4F7N/N2混合气体的分解路径,对各反应的正、逆向速率常数进行计算。引用弧后C4F7N/N2混合气体的温度衰减曲线,计算了C4F7N/N2混合气体各粒子浓度随时间的复原情况,并结合热力学平衡条件下各粒子浓度随温度变化的分解情况展开分析,可以得到如下结论:

1)C4F7N在温度0.5～0.7 kK时开始分解,2.5 kK时分解完全;N2在3 kK的温度下开始分解,在10 kK以上的高温下会大量分解。可见C4F7N分子不耐高温,较容易分解,而N2分子较为稳定。

2)在电弧温度高于10 kK的情况下,C4F7N和N2粒子将会快速分解,且分解后的大分子粒子在该温度下也很难存在,会快速分解成CFCF、CF2C、FCN等小分子粒子以及C、N、F等自由基粒子。

3)弧后温度随时间降低至2 kK左右,N2将会快速复原至摩尔分数70%以上,而C4F7N虽具有较强的电气性能,但在高温下容易分解且极难复合,若多次使用C4F7N/N2混合气体熄弧会使C4F7N的浓度含量降低,从而影响混合气体的绝缘性能。