高温条件下光谱线型模型对光谱反演的影响分析

曾思贤, 任 欣, 何浩轩, 聂 伟,2*

1. 华南理工大学电力学院, 广东 广州 510641

2. 中国科学院合肥物质科学研究院安徽光学精密机械研究所, 安徽 合肥 230031

引 言

高温流场诊断在燃烧化学[1-2], 能源热利用[3-4]以及工业过程控制[5-6]等领域都具有重要意义。 尤其是对于航空发动机及燃烧风洞等燃烧流场诊断, 需要对燃烧流场进行无干扰的高精度及快速测量[7-8]。

传统的接触式测量方法及采样测量方法, 例如气动式探针及热电偶等, 无法满足航空发动机等燃烧流场的高温、 高速(超声速)以及强湍流等环境下的高精度测量。 以拉曼光谱(Raman spectroscopy, RS)[9-10], 相干反斯托克斯拉曼光谱(coherent anti stokes Raman spectroscopy, CARS)[11], 激光诱导荧光(laser induced fluorescence, LIF)[12]以及可调谐二极管激光吸收光谱(tunable diode laser absorption spectroscopy, TDLAS)[1-2]等为代表的非接触式激光光谱测量技术具有非接触、 快速响应、 多参数检测等优势, 已经在高温流场原位测量中取得了广泛的应用。

其中, TDLAS技术具有结构简单, 鲁棒性好, 测量结果免标定以及易于小型化等优势, 非常适合于高温环境下流场参数(例如温度、 压力和流速等)的非接触测量[1-2, 13-14]。 采用TDLAS对流场参数进行测量过程中, 需要利用光谱线型模型拟合测量光谱, 获取测量光谱的积分吸光度值, 进而计算得到温度值。 所以, 光谱线型模型将直接影响光谱反演温度的精度。

根据光谱展宽机制的不同, 当前已发展了多种不同的光谱线型模型。 例如, Gaussian线型, Lorentz线型, Voigt线型, Speed-dependent Voigt线型, Rautian线型, Speed-dependent Rautian线型和Hartman-Tran线型等。 其中Gaussian线型, Lorentz线型分别单独考虑分子运动的多普勒效应及碰撞效应[15]。 同时考虑Gaussian展宽与Lorentz展宽的作用, 且展宽机制之间相互独立, 光谱线型可用Voigt线型描述[16]。 当考虑碰撞压窄(Dicke-narrowing)效应[17]时, 可构建Rautian线型[18]。 当考虑速度依赖(speed-dependent)效应[19]时, 可构建Speed-dependent Voigt线型, Speed-dependent Rautian线型等[20]。 同时考虑碰撞压窄效应与速度依赖效应时, 可构建Hartman-Tran (HT)线型[21]。

高温环境条件下, 由于不同光谱线型模型的展宽机制不同, 将会导致不同光谱线型拟合效果间存在差异性。 Goldenstein实验观察到了CO2和N2气氛中的水汽吸收光谱强烈的碰撞压窄效应(Dicke-narrowing), 然而在纯H2O中却不存在[22]。 然后, Goldenstein等利用Voigt, Rautian, Galatry和speed-dependent Voigt线型对1.4 μm附近的7条水汽吸收光谱的温度依赖系数进行了实验研究, 发现Voigt线型拟合大转动量子数J″的吸收线精度较差, 而Rautian, Galatry和speed-dependent Voigt线型拟合效果较好[23]; 但Buchholz等认为Rautian, Galatry和HT等线型模型的稳定性及可靠性会严重受限于测量光谱的信噪比, 虽然Voigt忽略了高阶效应, 在低信噪比条件下却更适用[24]。 我们之前的研究[25]证明了Voigt线型和HT线型获取的光谱积分吸光度大小一致性较好, 而其他光谱参数(例如展宽系数)差异性较大。 尽管这些研究采用了几种不同的光谱线型模型提取光谱参数并进行了对比。 但是, 不同光谱线型获取的高温光谱参数的差异性以及导致气体状态参数(例如温度)的反演精度的影响认识并不够全面和清晰。 因此, 仍需进一步发展适合于高温光谱反演的光谱线型选择策略。

本工作首先利用实验室的高温光谱实验平台, 选择适合高温环境温度测量的吸收线, 采用TDLAS技术获取水汽在1 100～1 600 K温度范围内的吸收光谱。 然后分别采用7种不同光谱线型模型进行L-M最小二乘拟合, 获取测量光谱的积分吸光度, 速度依赖线宽和多普勒半高宽, 并采用双线比值法计算得到水汽温度。 并对比不同线型模型在程序中的运行时间, 对比分析获取不同光谱线型模型对高温光谱反演的差异性, 为高温环境下光谱诊断的光谱线型选取提供参考。

1 TDLAS测量温度原理

可调谐二极管激光吸收光谱(TDLAS)技术的基本原理是Lambert-Beer定律, 可由式(1)描述。

(1)

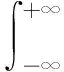
根据式(1), 我们可以得到积分吸光度为

(3)

在高温环境下, 两条吸收线的线强比值可推导为

(4)

由于相同环境下的两条吸收线, 其测量路径上的压力、 组分浓度, 有效吸收光程路径长度都相同, 根据式(3)和式(4), 可得到测量光路径上的平均温度为

(5)

根据式(5)可以看出, 测量光路径上的平均温度取决于测量光谱的积分吸光度之比。 通过光谱线型模型, 例如Gaussian线型, Lorentz线型, Voigt线型, Speed-dependentVoigt线型, Rautian线型, Speed-dependent Rautian线型和Hartman-Tran线型, 拟合测量光谱即可获取积分吸光度值, 同时可获得光谱的多普勒半高宽和速度依赖线宽, 可分别表示为

(6)

(7)

其中, ΔνD为光谱的多普勒半高半宽(HWHM),T为气体温度,M为相对分子质量。 ΔνC为光谱的速度依赖线度。γi-j(T0)(cm-1·atm-1)为参考温度T0下组分i、j之间的碰撞展宽半高半宽,ni-j为温度依赖系数。

2 吸收线的选择

高温温度的精确测量要求光谱吸收线对高温温度具有足够的敏感性。 Ma等[26]提出了TDLAS温度测量吸收线选择策略。 Cheong等[27]采用数值方法和实验方法研究了吸收线选择对高温火焰温度和浓度分布测量结果的影响, 提出了适用于高温检测的吸收线选择原则。 基于这些策略和原则, 我们选择7 467.77和7 179.75 cm-1两条吸收线用于高温环境中的水汽测量。 表1给出了HITRAN 2020数据库[28]中这两条吸收线的线参数。

表1 HITRAN 2020数据库中的水汽吸收线参数

由于7 179.75 cm-1这条吸收线中包含两条波长接近的吸收线(7 179.751 5与7 179.752 0 cm-1), 实际测量到的光谱会重叠, 因此可将两条吸收线叠加为一条吸收线进行处理[29]。 首先计算了所选两条吸收线在不同温度下的线强、 线强比及相对测温灵敏度, 计算结果如图1所示。 从图中可以看出, 在700 K以下, 两条吸收线的线强相差较大, 由于温度依赖特性的差异性, 当温度高于700 K, 两吸收线的线强差逐渐减小。 而线强比值(橙色)随温度的变化线性变化, 因此可以通过线强比获取温度值。 从相对温度测量灵敏度(粉色)随温度的变化规律中可以看出, 在1 800 K以下, 相对温度灵敏度均大于1, 这说明所选吸收线线对在实验温度范围(1 100～1 600 K)内具有足够的灵敏度。

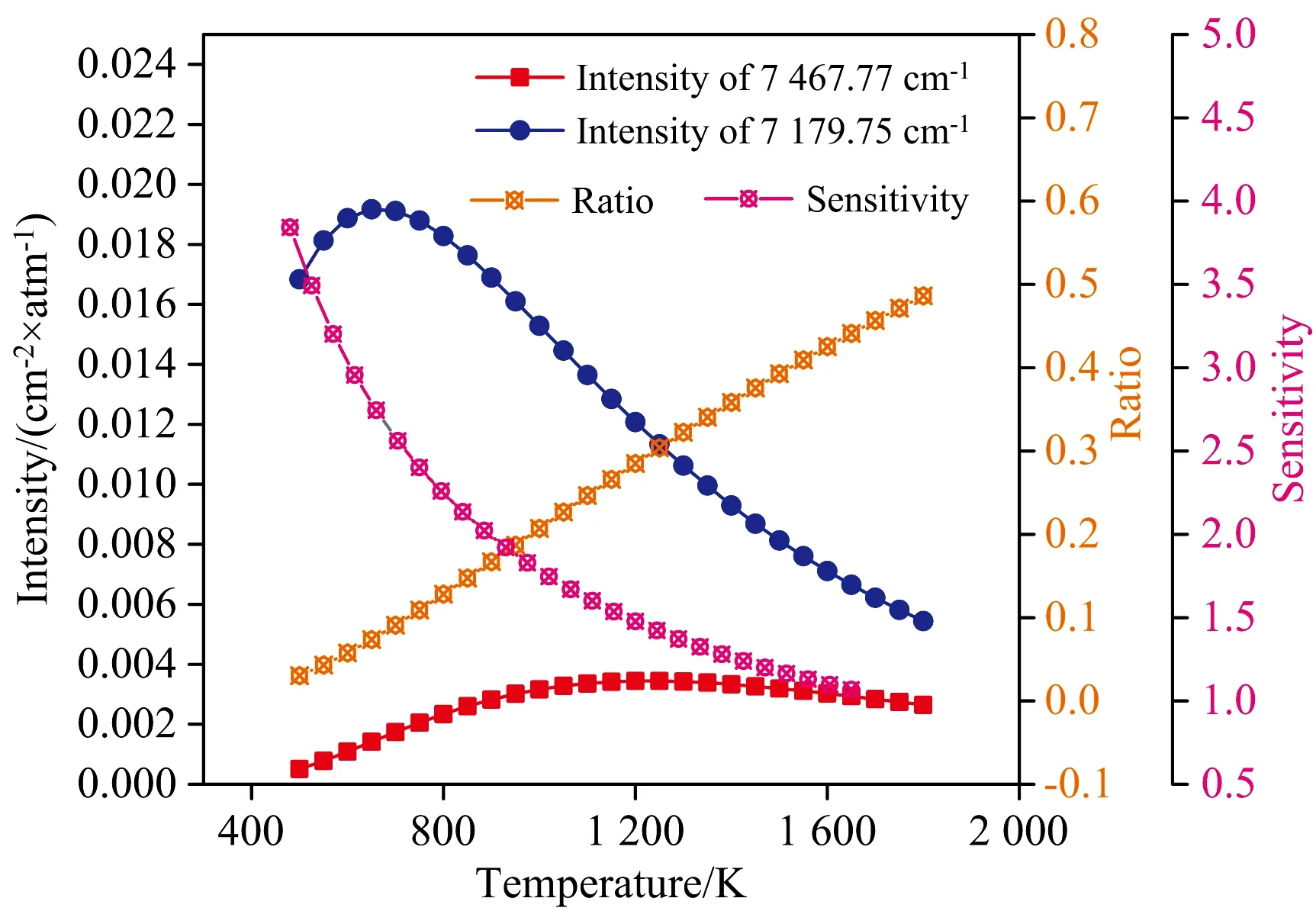
图1 吸收线7 467.77和7 179.75 cm-1在不同温度下的线强, 线强比值及相对测温灵敏度

3 实验及结果与讨论

为了探究光谱线型模型对光谱反演精度的影响, 利用实验室的高温炉, 搭建了如图2所示的实验装置, 用于测量水汽吸收光谱。 高温炉有三个温度区域, 其中待测气体所处区域为恒温区, 其他两个区域为氮气区。 利用时分复用技术, 通过调节激光器温度和电流驱动, 使两只分布反馈式(distributed feedback, DFB)二极管激光器出射激光的波长覆盖所选吸收线。 激光器出射激光首先经过分束器分为两束, 其中一束经准直器1准直后直接穿过高温炉恒温区的待测气体, 由探测器1接收, 用于获取水汽吸收信号。 为了避免大气环境中的水汽对测量信号的干扰, 设置了两个隔离罩, 分别将激光发射端和接收端在大气中的部分置于隔离罩内, 并采用高纯氮气连续吹扫, 从而减小空气中水汽的影响。 另一束经过准直器2后穿过标准具, 由探测器2接收, 此信号用于激光波长标定。

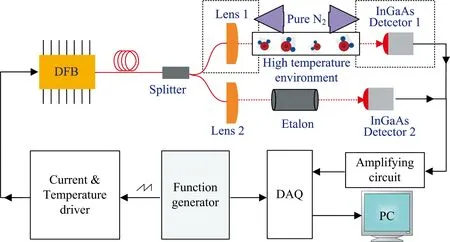
图2 实验装置图

控制激光器驱动温度不变, 通过调谐驱动电流的方式实现激光器输出波长的快速调谐。 设置调谐频率为1 kHz, 数据采样率为7 MSA·s-1。 分别设置高温炉温度为1 100、 1 200、 1 300、 1 400、 1 500和1 600 K, 待温度稳定后连续测量10组水汽吸收数据。

探测器1获取的水汽吸收数据, 经过探测器2测量的干涉信号标定波长后, 最终得到水汽吸收光谱信号。 我们分别利用Gaussian, Lorentz, Voigt, SDVoigt, Rautian, SDRautian和Hartman-Tran光谱线型模型, 结合L-M算法, 对测量光谱进行逐个拟合, 并获取测量光谱的积分吸光度, 多普勒半高宽和速度平均线宽。 图3给出了采用7种线型拟合两条吸收光谱(7 467.77和7 179.75 cm-1)的结果及残差。 我们利用拟合残差的1倍标准差来评估拟合效果。 以7 179.75 cm-1吸收线拟合结果为例, Gaussian线型的拟合效果最差, 拟合残差的标准差最大, 约为8.12×10-3; Lorentz线型拟合存在一个“M”型残差, 说明Lorentz线型获取的光谱线型比测量光谱“更矮更胖”, 且残差的标准差为1.56×10-3; Voigt线型拟合存在“W”形残差, 说明Voigt线型获取的光谱线型比测量光谱“更高更窄”, 且残差的标准差为1.63×10-3; 高阶的SDVoigt线型, Rautian线型, SDRautian线型和HT线型拟合效果均较好, 残差标准差大小基本相同, 约为8.78×10-4。

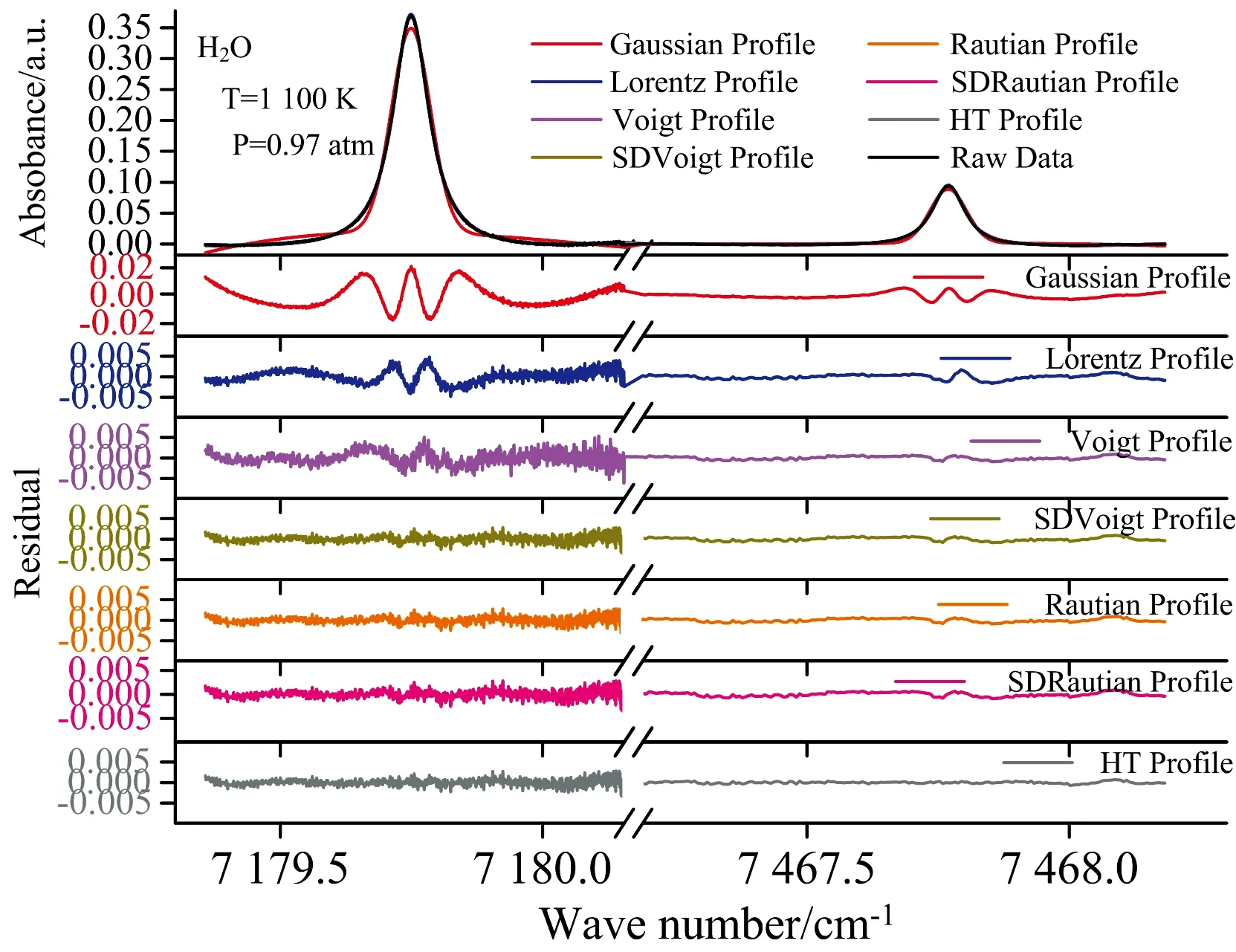
图3 不同光谱线型拟合实验光谱结果及拟合残差

通过光谱线型模型拟合测量光谱可获取光谱线型参数, 其中图4和图5分别给出了7 467.77和7 179.75 cm-1两条吸收线经7种光谱线型拟合得到的积分吸光度, 速度平均线宽及多普勒半高半宽。 由图4(a)和图5(a)可以看出, Gaussian线型(GP)获取的积分吸光度偏小, Lorentz线型(LP)获取的积分吸光度偏大, Voigt线型(VP), SDVoigt线型(SDVP), Rautian线型(RP), SDRautian线型(SDRP)和Hartman-Tran线型(HTP)模型获取的积分吸光度结果相近。 但是同一温度下, 不同线型获取的洛伦兹展宽和高斯展宽之间存在较大的差异性, 如图4(b)、 (c)和图5(b)、 (c)所示。 另外, 根据式(6)可知, 多普勒半高半宽的拟合结果与温度变化间的关系不相符, 说明了拟合的不确定性较大。

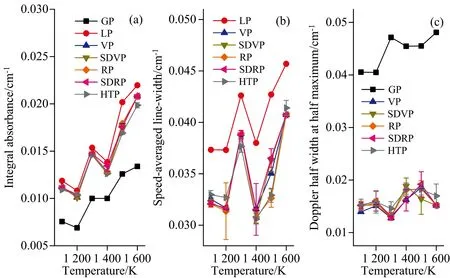
图4 采用7种光谱线型获取的吸收线7 467.77 cm-1的线型参数

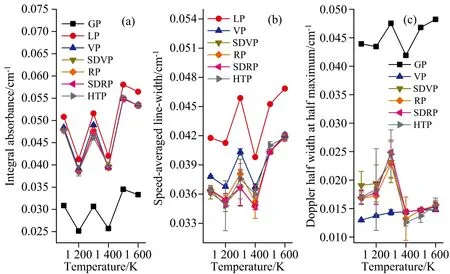
图5 采用7种光谱线型获取的吸收线7 179.75 cm-1的线型参数

根据式(6)可知, 对于确定的吸收线, 多普勒半高半宽为温度的单值函数。 我们首先通过温度计算多普勒半高半宽值, 并将其设置为已知量以减少拟合过程的变量数。 然后采用L-M算法, 分别用7种线型函数拟合测量光谱, 图6和图7为拟合获取的线型参数结果。 由图6(a)和图7(a)可以看出, 固定多普勒半高半宽值之后, Gaussian线型获取的积分吸光度明显偏小, Lorentz线型获取的积分吸光度偏大, Voigt线型获取的积分吸光度相比高阶非Voigt线型(SDVP, RP, SDRP和HTP)获取的积分吸光度结果偏小, 而高阶非Voigt线型获取的积分吸光度一致性较好。 由图6(b)和图7(b)可以看出, 固定多普勒半高半宽值之后, 拟合获取的速度平均线宽的变化趋势一致, 但Lorentz线型获取的速度平均线宽偏大, Voigt线型获取的速度平均线宽偏小, 4个高阶非Voigt线型获取的速度平均线宽间的偏差较小。 说明通过固定多普勒半高宽, 可有效光谱提高拟合的精度和稳定性。

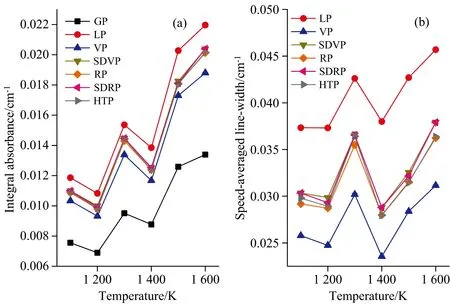
图6 固定多普勒半高宽后的7 467.77 cm-1线型参数拟合结果

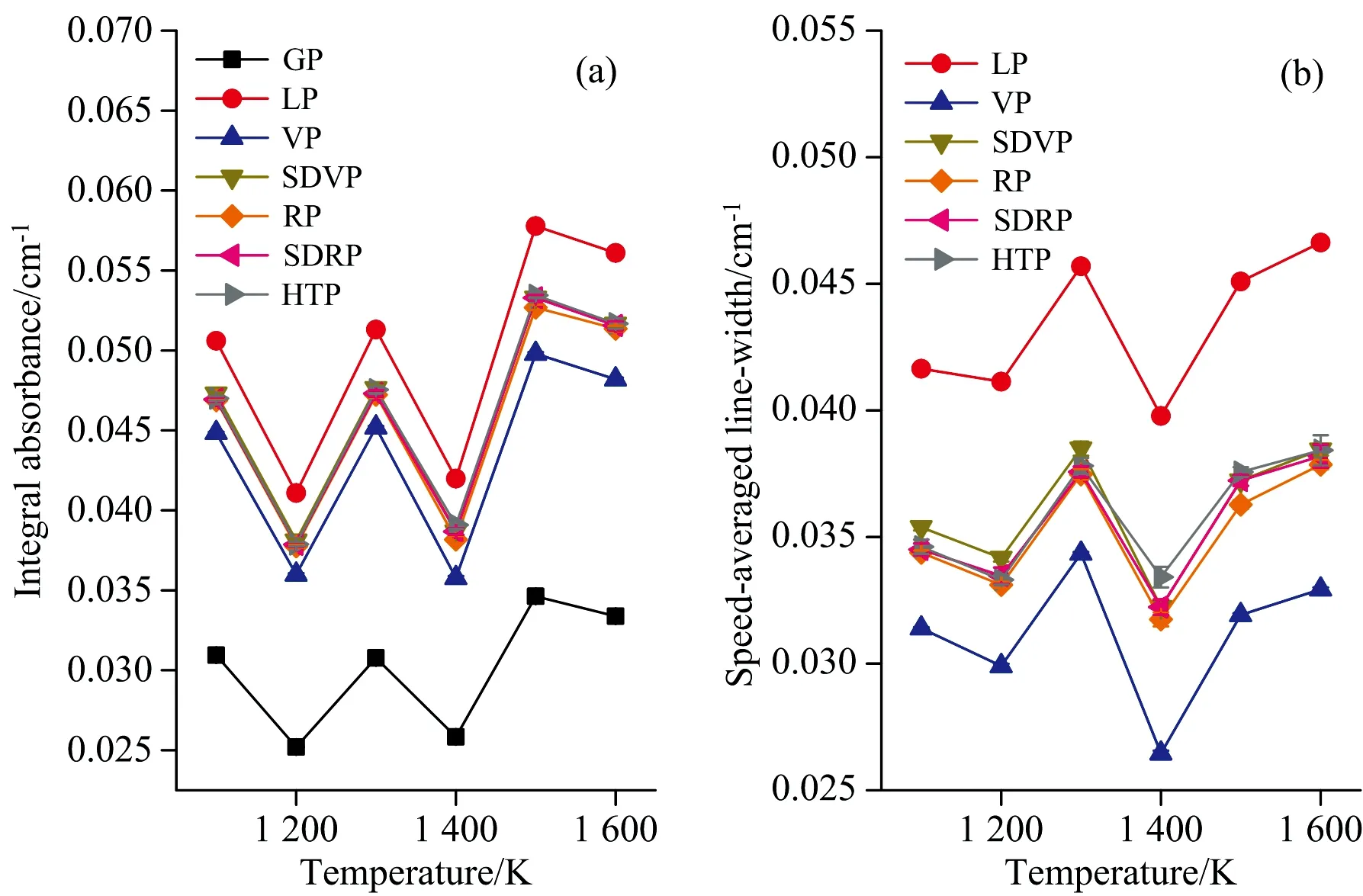
图7 固定多普勒半高宽后的7 179.75 cm-1线型参数拟合结果

获取积分吸光度后, 根据双线比值方法计算得到气体温度, 并通过与高温炉中热电偶测量的温度对比并计算测量偏差, 如图8和图9所示。 其中图8是多普勒半高宽不固定条件下的温度计算结果, 图9是固定多普勒半高宽后的温度计算结果。

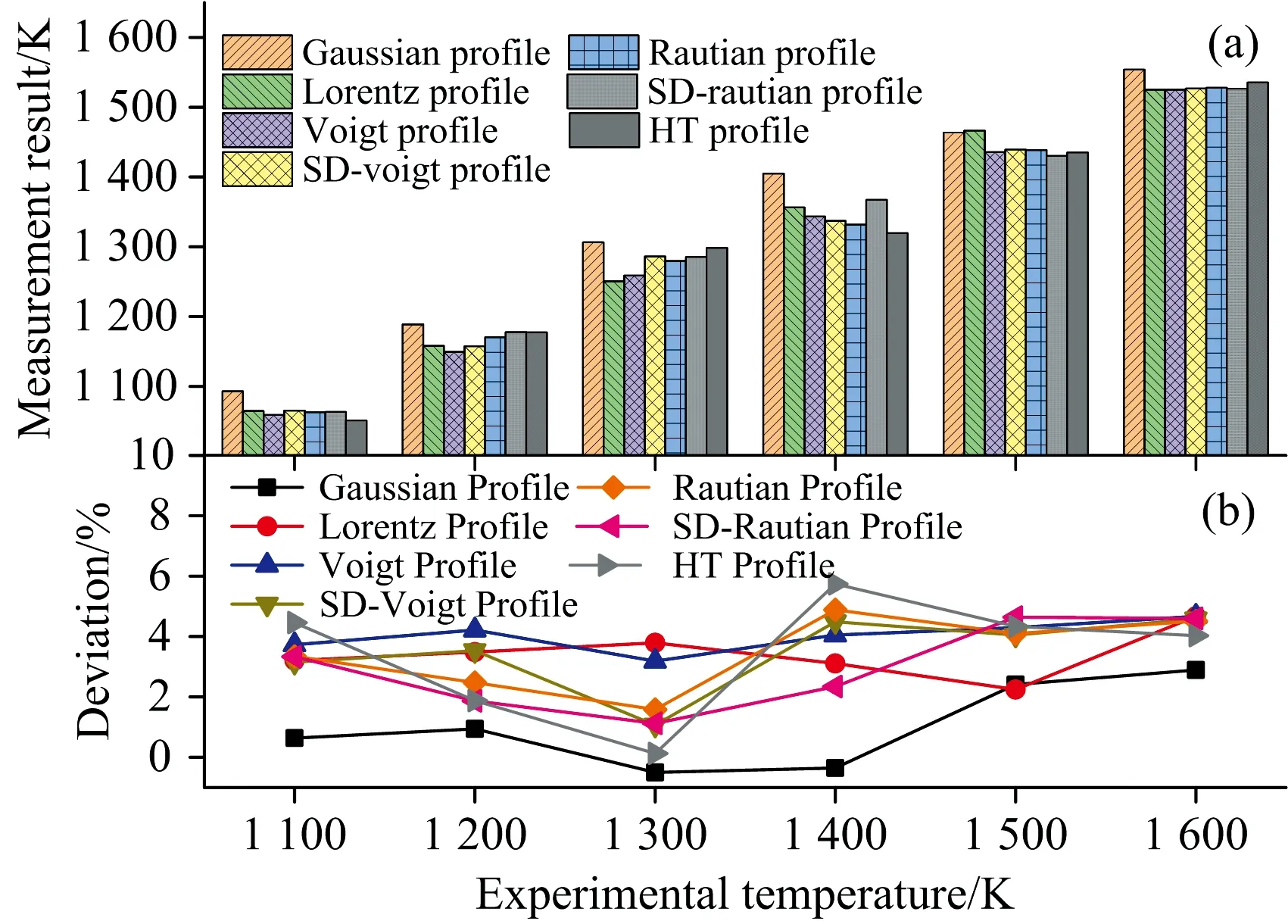
图8 多普勒半高宽不固定条件下的温度测量结果

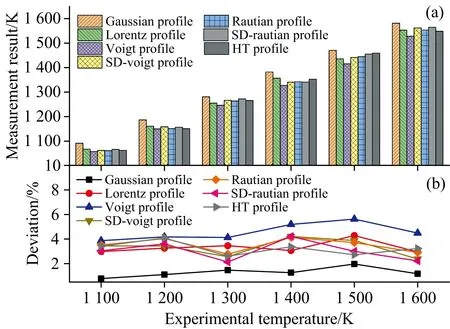
图9 多普勒半高宽固定条件下的温度测量结果

对比图8和图9中的结果可以看出, 无论多普勒半高宽固定与否, 通过Gaussian线型获取的温度精度都最高。 但是, 固定多普勒半高宽后, 不同光谱模型的拟合结果计算的温度精度有所提高, 而且不同温度下测量的波动性更小。 另外, Voigt线型反演的温度偏差最大。

由于Gaussian线型和Lorentz线型模型简单, 相比Voigt线型函数变量较少, 而高阶的非Voigt线型函数复杂, 变量较多, 在拟合过程计算的耗时将更长。 以拟合7 467.77 cm-1吸收线为例, 分别分析固定多普勒半高宽(方法1)和不固定多普勒半高宽(方法2)两种情况下不同光谱线型拟合程序的运行时间, 如表2所示。

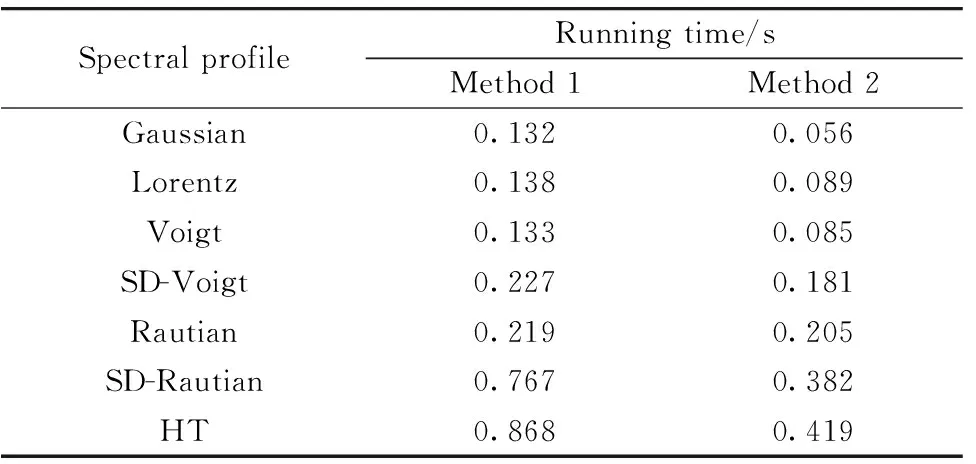
表2 不同光谱模型拟合程序的运行时间

由表2可以看出, 高阶光谱线型, 尤其是SD-Rautian线型和HT线型运行时间约为Gaussian, Lorentz和Voigt线型的7倍。 因此, 对于高速在线测量, 在保证光谱拟合精度的条件下, 高阶的SD-Voigt或Rautian光谱模型最优。

4 结 论

为了探究高温条件下光谱线型模型对光谱反演的影响, 对比分析了7种光谱线型模型获取高温光谱的积分吸光度, 速度依赖线宽和多普勒半高半宽等线型参数的差异性, 并采用双线比值法计算了不同光谱线型获取的气体温度。 高阶非Voigt线型(SDVoigt, Rautian, SDRautian和HT线型)拟合效果明显优于Gaussian和Lorentz线型, 这使得采用Gaussian和Lorentz线型获取的积分吸光度与高阶非Voigt线型差异较大。 高阶非Voigt线型获取的积分吸光度一致性较好, 但是高阶非Voigt线型在拟合程序中的运行耗时更长, 且不同光谱线型获取的速度依赖线宽和多普勒半高宽参数结果差异性及波动性均较大。 但是, 通过温度计算多普勒半高宽并将其固定为线型模型函数的已知量这一方法, 不仅可以有效提高模型参数的拟合精度, 还提高了拟合的稳定性。 从拟合结果来看, 高阶非Voigt线型获取的积分吸光度和速度依赖线宽差异性均较小, 而Voigt线型获取的积分吸光度和速度依赖线宽均比高阶非Voigt线型获取的结果偏小。 对比温度结果可以看出, 固定多普勒半高宽和不固定多普勒半高宽两种光谱处理方法下的Gaussian线型温度反演精度均最高, 最大偏差约为2.89%, 而通过Voigt线型反演的不同温度均比其他线型获取的结果偏差大。 因此, 通过实验及计算分析, 在实际应用中, 我们采用如下吸收线选择策略: 通过Gaussian线型拟合获取温度, 然后基于温度结果计算多普勒半高宽, 并将其在模型函数中设置为已知量, 并采用高阶的SDVoigt线型模型拟合测量光谱。 这不仅能有效提高光谱线型参数和流场的反演精度, 还能有效提高光谱反演速度。 这将对高温光谱的高速、 在线及高精度反演发挥积极作用。